Захотел я однажды вычислить квадратный корень с помощью нормальных алгоритмов Маркова (НАМ).
Кратко о НАМ:
Итак, вроде бы все просто? Однако, как писать программы на НАМ?
Для себя я сделал примерно такой план:
Итак, вернемся к вычислению квадратного корня. Мы будем использовать «детский» метод (он же арифметический), который основывается на том простом факте, что квадрат числа — это сумма нечетных чисел от 1 до 2n-1:
Как бы мы могли реализовать извлечение корня основываясь на этом свойстве? Мы будем последовательно отнимать от числа сначала 1, потом 3, потом 5 и т.д., пока число не станет меньше нуля, паралельно считая сколько отниманий мы сделали. Итого, уже два счетчика + одна переменная для хранения результата
Маленькая особенность НАМ — нету здесь чисел. И переменных нету. Поэтому нам надо бы симулировать их. Так как писать длинн��ю арифметику мне было лень (да и сомневаюсь что это возможно человеку), то арифметические операции сделал по простому принципу — с помощью инкремента и декремента.
Я решил сделать так, чтобы у меня строка хранилась в формате {Результат}.{Число}{ОчередноеНечетноеЧисло}{ИндикаторКонцаСтроки}
Нечетное число я решил хранить в унарной системе исчисления и обозначать единицу как "#" — так гораздо проще работать будет.
Теперь, каким образом мы будем отнимать от числа очередное нечетное, не потеряв данные? Я решил, что между нечетным число и индикатором конца строки нужно добавить маркер «a», который перемещаясь сквозь число будет его дублировать, но уже в другом виде (обозначаем через "-"). После будем сдвигать все минусы к числу и отнимать их. После того как мы все числа отняли, нам нужно увеличить результат на единицу.
В моей реализации была маленькая особенность — результат всегда выходит округленным вверх. Я решил сделать так, чтобы этот алгоритм работал с абсолютной точностью 0.5, а не 1 (как в описании). Когда в строке остается минусов больше чем половина от их начального значения, мы должны взять и уменьшить результат.
В итоге получился «пинг-понг», который извлекает квадратный корень заданного числа.
Очень интересно выглядит зависимость количества замен от числа: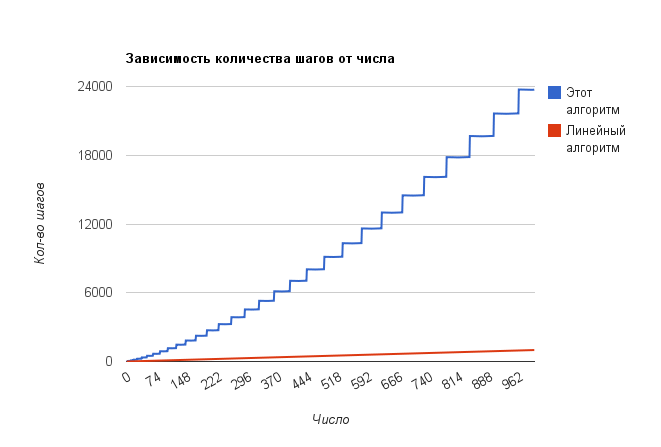
Посмотреть код: paste.org.ru/?3uweqh
Посмотреть пример выполнения: paste.org.ru/?34caeb
Скачать программу: sites.google.com/site/nsinreal/markovsqrt.zip
Кратко о НАМ:
- Существует список замен одной подстроки на другую, называемых правилами
- Ищем с начала списка первое правило которое можем применить и применяем его для первого вхождения
- Если такое правило было обнаружено, то возвращаемся к предыдущему пункту и просматриваем список правил сначала
- Если правило было заключительным, то завершаем работу
- Если больше нет правил, которые мы можем применить, то завершаем работу
Итак, вроде бы все просто? Однако, как писать программы на НАМ?
Для себя я сделал примерно такой план:
- Пытаемся написать обычный алгоритм использующий только строки
- Следим за тем, чтобы последние замены не пересекались с первыми
- Переворачиваем алгоритм и записываем с конца к началу
Итак, вернемся к вычислению квадратного корня. Мы будем использовать «детский» метод (он же арифметический), который основывается на том простом факте, что квадрат числа — это сумма нечетных чисел от 1 до 2n-1:
- 1 = 12 = 1
- 1 + 3 = 22 = 4
- 1 + 3 + 5 = 32 = 9
Как бы мы могли реализовать извлечение корня основываясь на этом свойстве? Мы будем последовательно отнимать от числа сначала 1, потом 3, потом 5 и т.д., пока число не станет меньше нуля, паралельно считая сколько отниманий мы сделали. Итого, уже два счетчика + одна переменная для хранения результата
Маленькая особенность НАМ — нету здесь чисел. И переменных нету. Поэтому нам надо бы симулировать их. Так как писать длинн��ю арифметику мне было лень (да и сомневаюсь что это возможно человеку), то арифметические операции сделал по простому принципу — с помощью инкремента и декремента.
Я решил сделать так, чтобы у меня строка хранилась в формате {Результат}.{Число}{ОчередноеНечетноеЧисло}{ИндикаторКонцаСтроки}
Нечетное число я решил хранить в унарной системе исчисления и обозначать единицу как "#" — так гораздо проще работать будет.
Теперь, каким образом мы будем отнимать от числа очередное нечетное, не потеряв данные? Я решил, что между нечетным число и индикатором конца строки нужно добавить маркер «a», который перемещаясь сквозь число будет его дублировать, но уже в другом виде (обозначаем через "-"). После будем сдвигать все минусы к числу и отнимать их. После того как мы все числа отняли, нам нужно увеличить результат на единицу.
В моей реализации была маленькая особенность — результат всегда выходит округленным вверх. Я решил сделать так, чтобы этот алгоритм работал с абсолютной точностью 0.5, а не 1 (как в описании). Когда в строке остается минусов больше чем половина от их начального значения, мы должны взять и уменьшить результат.
В итоге получился «пинг-понг», который извлекает квадратный корень заданного числа.
Очень интересно выглядит зависимость количества замен от числа:

Посмотреть код: paste.org.ru/?3uweqh
Посмотреть пример выполнения: paste.org.ru/?34caeb
Скачать программу: sites.google.com/site/nsinreal/markovsqrt.zip