
Многим известна игра «Жизнь», изобретенная Дж.Конвеем еще в 1970 г. Еще шире известен один из объектов этой игры – планер (или глайдер) – движуееся образование из 5 клеток:
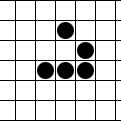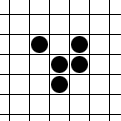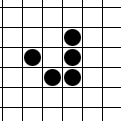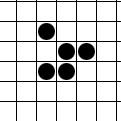 .
. В 1987 г. Были найдены первые планеры в трехмерных версиях «жизни» ( www.complex-systems.com/pdf/16-4-7.pdf ). К сожалению, из случайных конфигураций они возникают очень редко (в отличие от двумерной версии). Я решил поискать правила игры, в которых планеров было бы побольше.
Напомню правила. Есть некоторая регулярная решетка. У каждой ее ячейки (клетки) определено множество соседей (в случае квадратной сетки на плоскости обычно берут 8 соседей, а для кубической сетки в пространстве – 26). Каждая клетка может быть либо живой, либо мертвой. За каждый такт времени мертвые клетки, число живых соседей которых принадлежит некоторому множеству B, оживают, а живые клетки, число живых соседей которых не принадлежит множеству – погибает. Пара S/B определяет законы развития. Например, классическая игра Конвея имеет правила S2,3/B3 (или B3/S2,3 – в разных местах пишут по-разному, поэтому буквы B и S лучше оставлять).
В зависимости от правил, развитие конфигурации клеток может быть разным. В некоторых случаях случайная конфигурация рано или поздно полностью вымирает:
В других – она приходит к стабильному или периодическому состоянию:
В третьих – область с живыми клетками занимает все пространство, и мы видим только беспорядочное чередование живых и мертвых клеток:
И, наконец, в правилах четвертого типа компактные устойчивые структуры демонстрируют сколь угодно сложное поведение. Найти такие правила – мечта любого исследователя, кот��рому не лень этим заниматься, но это совсем не просто. Пример таких правил – собственно игра Конвея. Есть ли другие, я не знаю.
Как искать планеры? Первое, что приходит на ум – берем некоторый диапазон правил. Например, рождаться могут только клетки, у которых от 5 до 9 соседей, а оставаться в живых – у которых от 4 до 10 соседей. Это дает 4096 возможных правил, а учитывая, что хоть кто-то должен рождаться – еще меньше. Берем куб 200x200x200. Заполняем его центральную область размером 100x100x100 случайными клетками с некоторой плотностью, остальное пространство оставляем пустым. Перебираем все правила.
Для каждого правила просчитываем несколько поколений конфигурации – чтобы уменьшить влияние первоначального хаоса (я взял 60, но это с запасом). Смотрим, сколько живых клеток у нас осталось и сколько изменилось на последнем шаге.
Если осталось больше 100000 клеток или изменилось больше 50000 – говорим, что у нас правило 3-го типа, которое интереса не представляет. Может быть, активная область займет все пространство, а может быть, останется в пределах исходного куба – не очень важно, искать в ней устойчивые стуктуры мы не собираемся (хотя возможно, они там найдутся, если свернуть картинку с подходящим ядром).
Если изменившихся клеток нет, то тоже отбрасываем правило, оно 1-го или 2-го типа: считаем, что если у нас бывают планеры, то хотя бы несколько пульсаров должно получится из любой конфигурации.
В остальных случаях просчитываем эволюцию дальше, порциями по 60 поколений. Проверяем оба предыдущих условия, а кроме того, проверяем, не вернулась ли за 60 шагов конфигурация в прежнее состояние. Если вернулась, значит развитие окончено – но пульсары существуют. Запоминаем правило для дальнейшего исследования.
Кроме того, проверяем, не подобрались ли живые клетки к границе куба (например, на расстояние 10). Если да, то у нас большие шансы на то, что обнаружен планер. Или еще что-нибудь интересное.
Если развитие дошло до 1200-го поколения и не прекратилось ни по одной из вышеуказанных причин, то правило все равно остается в списке подозрительных, запоминаем его.
Теперь просматриваем список «подозрительных» правил, и начинаем исследовать их вручную.
План казался хорошим, и с его помощью я нашел несколько новых планеров. Но довольно быстро обнаружил, что картина развития может выглядеть так:
В основном, эволюция ведет себя как правило второго типа, но если в каком-то месте плотность оказывается больше критической, там возникает активная область, которая в итоге разрастается на все пространство. В работе Бейса такие правила сразу отбрасываются, как нарушающие условие «ограниченности роста случайных конфигураций». Мне их отбрасываеть не хотелось, поэтому алгоритм перебора пришлось усложнить.
Теперь я для каждого правила просчитываю не одну, а четыре случайных конфигурации – с плотностью живых клеток 3%, 6%, 12% и 24% (числа взяты с потолка, но мне они показались достаточно разумными). Дальше следую вышеописанному алгоритму, но запоминаю не только правила, но и плотнос��ь.
Первый этап отбора прошли 984 конфигурации из 15872. Просматривать их вручную было слишком долго, поэтому следующий уровень отбора тоже достался компьютеру.
Просматриваем правила и плотности конфигураций. Для каждой – берем 4 значения плотности, близкие к записанному (для более тонкой настройки), для каждого значения строим два случайных заполнения, и обрабатываем их тем же алгоритмом, что и на первом этапе. Но на этот раз нас интересуют только планеры (конфигурации, живые клетки которых достигли границы куба), и, на всякий случай, не стабилизировавшиеся конфигурации (просчитанные до поколения 1200). Мало ли, что там у них происходит?
Для всех конфигураций, прошедших второй этап отбора, сохраняем стартовые условия (правила, плотность и стартовое значение RND) для дальнейшего исследования.
Общее количество правил, прошедших второй этап – 30. У некоторых записалась всего одна стартовая конфигурация, у других – несколько десятков.
Начинаем смотреть.
Первое правило, с которого началась популяризация трехмерной «жизни» – B5/S4,5 («примечательна тем, что все параметры ровно на 2 больше, чем в классической версии»). Действительно, программа нашла и это правило, и планер. При плотности около 18% конфигурация стабилизируется примерно за 100 поколений, остается 450-500 живых клеток (плотность 0.05%), вероятность появления планера примерно 1/10 (т.е. 1 на 10 млн. клеток объема).
В списке оказалось еще несколько похожих правил: B5/S4,5,9; B5/S4,5,10; B5,9/S4,5,9; B5,9/S4,5,10
Но если во втором из этих правил планер выглядит так же, как в B5/S4,5, то в первом чаще появляется другой, более легкий тип:
В двух последних правилах планеры совсем другие. В B5,9/S4,5,9 их два (с периодами 4 и 6): первый – такой же, как на предыдущей картинке, а второй такой:
Причем у них не всегда есть шанс выжить
Может быть, в бесконечном пространстве планер успел бы улететь от активной области, но в замкнутой вселенной шансов нет.
А в правиле B5,9/S4,5,10 есть легкий планер с периодом 2:
Но эти правила – не самые популярные в списке. Больше всего мест там занимает B6/S5,7 и его «усиления» (B6/S5,6,7 и т.п.) Если посмотреть на планеры, возникающие в них, то станет понятно, в чем дело:
Если взять конфигурацию из «жизни» Конвея, в которой ни у одной пустой клетки нет 6 соседей (а у живой – 5) и записать ее в «два слоя», то в правиле B6/S5,7 она будет вести себя точно так же, как оригинал. Поэтому в пространстве появляются «блоки», «ящики», «мигалки» и другие простые фигуры. К сожалению, планерное ружье там не выживет.
Пример развития с самого начала:
Но, конечно, в этой вселенной встречаются и другие объекты, не имеющие аналогов в 2D…
Это только начало. При других правилах попадаются другие разновидности планеров, и еще много интересного. Так что продолжение следует…