Хабр Курсы для всех
РЕКЛАМА
Практикум, Хекслет, SkyPro, авторские курсы — собрали всех и попросили скидки. Осталось выбрать!
Хабр доступен 24/7 благодаря поддержке друзей
Комментарии 149
В числе фибоначи O(N) цифр, а потому его быстрее чем за O(N) найти нельзя. Быстро можно находить только числа фибоначи по какому-нибудь модулю.
Есть два возражения.
1.
> В числе фибоначи O(N) цифр
Почему вы так решили?
2.
> а потому его быстрее чем за O(N) найти нельзя
Это имело бы смысл, если бы я вычислял число по одной цифре, но это не так.
1.
> В числе фибоначи O(N) цифр
Почему вы так решили?
2.
> а потому его быстрее чем за O(N) найти нельзя
Это имело бы смысл, если бы я вычислял число по одной цифре, но это не так.
1. Потому что для них есть явная формула, в которую входит экспонента.
Ну и тривиальная грубая оценка. Если f_n > 2^{n/2}, f_{n+1} > 2^{n/2}, то f_{n+2} > 2^{n/2 + 1} = 2^{(n+2)/2}. Ну и далее по индукции f_k > 2^{k/2} для всех достаточно больших k.
2. Вы не можете быстрее чем за O(N) даже вывести результат (ну или сохранить его в память).
Ну и тривиальная грубая оценка. Если f_n > 2^{n/2}, f_{n+1} > 2^{n/2}, то f_{n+2} > 2^{n/2 + 1} = 2^{(n+2)/2}. Ну и далее по индукции f_k > 2^{k/2} для всех достаточно больших k.
2. Вы не можете быстрее чем за O(N) даже вывести результат (ну или сохранить его в память).
2. Теория с практикой иногда расходятся. Если некоторый гипотетический алгоритм (на конкретной машине, в конкретных условиях) работает за 0.0001*n + 10000*log(n), теоретик увидит в этом O(n) + O(log n) = O(n), а практик поймет, что существует довольно широкий диапазон входных данных, в пределах которых система практически ведет себя как O(log n). Если бы такого подхода не существовало, то в 2002-ом (!) году Python не перереализовывал бы свою сортировку с исользованием http://en.wikipedia.org/wiki/Timsort и никто бы никогда не говорил, что на практике Quicksort практически всегда быстрее Heapsort.
Это абсурд. Жонглирование размытыми категориями типа «практически всегда» не делает O(log n) из O(n).
Понятно, что на практике всё может повести себя быстрее, на каких-то данных, несмотря на то, что по теории сложностей может быть картина даже противоположная. Тот же mergesort, из которого был сделан timsort тоже на некоторых данных даёт O(n), а в среднем O(n log n), всё как и в timsort. Что же это значит, зачем тогда делали timsort? Что вообще значит «практика» применительно к оценке через O?
Ясно, что это вещи из разных миров. Мне не захотелось ставить крест на алгоритме на основании алгоритмической сложности ввода-вывода, диктумой самой задачей, то есть, хотел заметить, что если задача не предполагает с теоретической точки зрения существования решения быстрее некоторой оценки через О-нотацию, то это еще не значит, что нужно прекращать поиски более оптимальных решений ее «ядра». Выразил наболевшее в не совсем удачном месте.
Как правило, лучший на практике в той или иной ситуации алгоритм является лучшим и с точки зрения O-нотации, если правильно выбрать единицы измерения или множество, по которому считается среднее.
Например, в данном случае нужно считать количество не элементарных операций, а арифметических — в этом случае мы действительно получаем O(log N) вместо O(N) (и в таком подсчете становится возможным найти ответ быстрее, чем за его размер).
Кроме того, если мы считаем сложность в простых операциях (за одну операцию можно выполнить арифметическое действие с числом не больше чем 2^32, но доступ к каждой ячейке занимает всё еще O(1)), то тут мы получаем O(log N) умножений и сложений чисел размера O(N), в тривиальном алгоритме — O(N) сложений чисел размера O(N). С учетом того, что сложение делается за O(N), а умножение уже алгоритмом Карацубы быстрее, чем за O(N^1.6), то получаем сложность тривиального алгоритма O(N^2), матричного — O(N^1.6 * log N). Т.е. матричный алгоритм лучше, т.к. log N < N^0.4 при достаточно больших N.
Например, в данном случае нужно считать количество не элементарных операций, а арифметических — в этом случае мы действительно получаем O(log N) вместо O(N) (и в таком подсчете становится возможным найти ответ быстрее, чем за его размер).
Кроме того, если мы считаем сложность в простых операциях (за одну операцию можно выполнить арифметическое действие с числом не больше чем 2^32, но доступ к каждой ячейке занимает всё еще O(1)), то тут мы получаем O(log N) умножений и сложений чисел размера O(N), в тривиальном алгоритме — O(N) сложений чисел размера O(N). С учетом того, что сложение делается за O(N), а умножение уже алгоритмом Карацубы быстрее, чем за O(N^1.6), то получаем сложность тривиального алгоритма O(N^2), матричного — O(N^1.6 * log N). Т.е. матричный алгоритм лучше, т.к. log N < N^0.4 при достаточно больших N.
Исчерпывающе, спасибо. Кстати, скорость умножения чисел все растет — быстрее и Карацубы, и упомянутого ниже Шёнхаге — Штрассена, алгоритм Фюрера, опубликованный в 2007 году. Его асимптотика — O(n*log(n)*(2^O(log*(n)))).
Да, кстати, если вы будете использовать БПФ для этих целей, то вы получите O(N*log^2(N)). Но можно поступить еще проще поступить — можно использовать Китайскую теорему об остатках, и тогда вы получите O(N*log(N)) против O(N^2). Тут прирост скорости очевиден.
В приведенной ссылке не написано, как восстанавливать число из остатков за N*log(N). Это вообще возможно?
Там число востанавливается за O(n^2 * log(k)) n — число простых модулей — т.е. по сути длинна числа / константу и k — максимальный из модулей (либо на нахождение гсд расширенным алгоритмом евклида). Однако такая операция производится только 1 раз, так что это не ухудшит ассимптотики. Как можно восстановить число за n*log(n) не слышал :)
Вот именно. Так что пока число умножений меньше, чем n, напечатать результат быстрее не получится. Для чисел Фибоначчи получаем O(n*log(n)+n^2)=O(n^2).
Пример хороший, но неудачный :(
Возможно, за счет быстрого умножения можно будет восстановить число за O(n^1.6*log(n)), но это все равно больше, чем O(n*log(n)).
Пример хороший, но неудачный :(
Возможно, за счет быстрого умножения можно будет восстановить число за O(n^1.6*log(n)), но это все равно больше, чем O(n*log(n)).
Да, пожалуй с китайской теоремой об остатках я погорячился :) Тогда посмотрим что нам дает БПФ. Оно позволяет нам выполнять перевод чисел за O(n*log(n)), их перемножение за O(n), и обратный перевод тоже за O(n*log(n)). Причем обратно мы можем переводить только после выполнения всех операций.
Тогда получается O(n*log(n)) — перево числа + O(n*log(n)) — возведение в степень + O(n*log(n)) — обратное преобразование. Итого в сумме O(n*log(n)).
Тогда получается O(n*log(n)) — перево числа + O(n*log(n)) — возведение в степень + O(n*log(n)) — обратное преобразование. Итого в сумме O(n*log(n)).
Посмотрим. К сожалению, после перемножения за O(n) нам нужно тут же вернуть число в позиционную запись, чтобы устранить переполнения в цифрах: когда мы перемножаем два N-значных числа в системе счисления K, то «цифра» результата ограничена N*K^2. Если будем перемножать 4 числа, ограничение будет N^3*K^4 (с каким-то коэффициентом). И так далее. Для возведения N-битного числа в степень M, нам надо работать с числами, имеющими порядка log(N)*M бит точности, и в сложность всех операций нам придется добавить (log(N)*M)^2.
Пока не очень понятно. Надо посмотреть, как оптимально выбрать точки для перенормировки. Но думаю, что лучше, чем O(n*log(n)^2) мы не получим — а они у нас и так есть, при перенормировке на каждом шагу.
Кстати, а позволит ли БПФ перевести число из двоичной записи в десятичную за O(n*log(n))? Понятно, что к числам Фибоначчи это отношения не имеет (мы можем сразу считать их в десятичной системе), но все-таки?
Пока не очень понятно. Надо посмотреть, как оптимально выбрать точки для перенормировки. Но думаю, что лучше, чем O(n*log(n)^2) мы не получим — а они у нас и так есть, при перенормировке на каждом шагу.
Кстати, а позволит ли БПФ перевести число из двоичной записи в десятичную за O(n*log(n))? Понятно, что к числам Фибоначчи это отношения не имеет (мы можем сразу считать их в десятичной системе), но все-таки?
По поводу точности я тоже думал, но тут все не так плохо :) Если Вы посмотрите ссылку которую я давал чуть выше, то там можно будет найти часть — Дискретное преобразование Фурье в модульной арифметике. Так вот, при использовании этой модификации данного метода Вы избавитесь от погрешностей и сохраните асимптотику, но ухудшите константу.
И еще один момент. На самом деле при использовании БПФ на каждом шаге, вы все равно получите асимптотику O(n*log(n)), потому что последний шаг по сложности будет покрывать все предыдущие, а асимптотика последнего шага как раз таки O(n*log(n)).
Что касается перевода числа из двоичной записи в десятичную я как то не задумывался. А как вы предлагаете действовать в это случае?
И еще один момент. На самом деле при использовании БПФ на каждом шаге, вы все равно получите асимптотику O(n*log(n)), потому что последний шаг по сложности будет покрывать все предыдущие, а асимптотика последнего шага как раз таки O(n*log(n)).
Что касается перевода числа из двоичной записи в десятичную я как то не задумывался. А как вы предлагаете действовать в это случае?
Модулярная арифметика погрешностей не отменяет: если вы считаете по большому модулю P, но значение «цифры» произведения (как суммы произведений определенных наборов цифр сомножителей) превысило эту величину, то при нормализации после обратного преобразования вы получите неверное предположение о значении этой цифры — и в итоге, ошибку в c*P*K^m.
Насчет последнего шага — согласен. Вот это действительно доказывает, что O(n*log(n)) возможно.
А про перевод я уже сказал — если от меня потребуется десятичное представление на выходе, то я просто все вычисления буду проводить в десятичной системе, для БПФ это не проблема (для нее числа — коэффициенты многочленов, а система счисления важна только при нормализации). Сам вопрос о быстром переводе 2<->10 отдельный, его надо изучать или искать.
Что же, результат получен :) Спасибо за обсуждение!
Насчет последнего шага — согласен. Вот это действительно доказывает, что O(n*log(n)) возможно.
А про перевод я уже сказал — если от меня потребуется десятичное представление на выходе, то я просто все вычисления буду проводить в десятичной системе, для БПФ это не проблема (для нее числа — коэффициенты многочленов, а система счисления важна только при нормализации). Сам вопрос о быстром переводе 2<->10 отдельный, его надо изучать или искать.
Что же, результат получен :) Спасибо за обсуждение!
При совсем больших n там вылезет еще множитель log(log(n))^2 (или log(log(n))): значение модуля, по которому считается БПФ, должно быть порядка O(n), и вычисления по этому модулю будут идти уже не за O(1). (в случае использования вещественной арифметики — аналогично). Но это уже о сложности сверхбыстрого умножения.
> В числе фибоначи O(N) цифр
Почему вы так решили?
Это же совсем очевидно: F_n имеет экспоненциальную асиптотику, а количество разрядов в экспоненте растет как O(n).
Не буду ссылаться на работы доказательств (в лицейские времена для Малой академии наук делалось), но для N-ого числа количество цифр лежит в промежутке (N/5; N/4) — то бишь, можно заявить о зависимости O(N). Основной факт для данного утверждения — в последовательности для каждого разряда (количества цифр в числе) существует не менее четырёх и не более пяти чисел.
По статье. Существует общая формула числа, в вычислении нуждаются только степени N-ого порядка иррациональных чисел. Если не брать во внимание сложность обработки длинных чисел, то да, таки O(logN).
По статье. Существует общая формула числа, в вычислении нуждаются только степени N-ого порядка иррациональных чисел. Если не брать во внимание сложность обработки длинных чисел, то да, таки O(logN).
Угу. Автор почему-то решил, что может выполнять арифметические операции над операндами любой разрядности за фиксированное время, но реализация длинной арифметики, похоже, возвращает предложенный алгоритм в класс O(N).
Хм, похоже, что вы правы.
Какой позорный косяк )
Какой позорный косяк )
Почему возвращает? Прямая итеративная реализация алгоритма поиска чисел Фибоначчи работает за O(N^2). Поэтому, если надо вывести в файл десятимиллионное число Фибоначчи, то обычная реализация будет работать на порядки дольше предложенной в решении. Поэтому алгоритм имеет смысл.
Мы на самом деле совещались, как сформулировать задачку одновременно корректно и интригующе, и пришли к формулировке в виде указания числа операций над числами, а не асимптотики. Ибо, если бы попросили найти за O(N), все бы удивились.
Мы на самом деле совещались, как сформулировать задачку одновременно корректно и интригующе, и пришли к формулировке в виде указания числа операций над числами, а не асимптотики. Ибо, если бы попросили найти за O(N), все бы удивились.
Тут числа перемножаются, а в прямой реализации складываются
Конечно, за O(N) все равно не получится из-за того, что большие числа все равно надо умножать, а это делается, хоть и не квадратично, но и не линейно. Если использовать умножения Шёнхаге — Штрассена для быстрого умножения чисел, то получим асимптотику чуть похуже O(N*log(n))
еще чуть хуже :)
Длинные числа можно перемножать за O(n), где n — длинна числа, если использовать Китайскую теорему об остатках. И того задача поставленная в статье задача решается за O(N*log(N)) против O(N^2) — общеизвестного решения. Думаю профит очевиден.
Тут я просто поленился точно оценить сложность, потому и написал «похоже, возвращает». В действительности всё, конечно, ещё хуже, вы правы.
А разве формула Бине не гарантирует O(1)?
Всё это замечательно. Даже если бы вы предложили вариант просчёта N-нного числа Фибоначчи за O(1), то остался бы ещё один (на мой взгляд намного более сложный) вопрос — практическое применение этого метода.
Я не слышал о полезном применении ряда Фибоначчи.
Гугл тоже не помог.
Кто-нибудь знает что-либо по этой теме?
Я не слышал о полезном применении ряда Фибоначчи.
Гугл тоже не помог.
Кто-нибудь знает что-либо по этой теме?
А как же кролики? А также всякие методы в трейдинге :)
Я не слышал о полезном применении ряда Фибоначчи.
- Fibonacci search
- Fibonacci heap
- И вот такое: A novel watermarking method
- И даже вот такое: Anti-collision in RFID system
Вообще, метод спокойно расширяется на все линейно-рекурсивные последовательности. Нужно просто знать как выводится матрица. Если хотите, расскажу
Хотим. Расскажите, пожалуйста.
Пусть у нас есть последовательность {x_n}, заданы x_0, ..., x_k и уравнение
x_{n+k} + a_{k} * x_{n+k} +… + a_0 * x_{n} = 0 при n > 0.
(для чисел Фибоначчи: k = 2, x_0 = x_1 = 1, a_2 = a_1 = -1: x_{n+2} — x_{n+1} — x_{n} = 0, т.е. x_{n+2} = x_{n+1} + x_{n}).
Рассмотрим вектора y = (x_{n+k+1}, x_{n+k}, ..., x_{n+1}) и z = (x_{n+k},… x_{n}:
Замечаем, что можно выразить y через z линейно:
y_{k+1} = x_{n+k+1} = — a_{k} * x_{n+k} — … — a_0 * x_{n} = -a_{k} * z_{k+1} — … — a_0 * z_{1}
y_{k} = x_{n+k} = z_{k+1}
…
y_{1} = z_{2}
Получаем, что y = A*z, где A — искомая матрица. Ее можно выписать явно:
((-a_{k}, -a_{k-1}, ..., -a_{0}),
(1, 0, ..., 0),
(0, 1, ..., 0),
...,
(0, 0, ..., 1, 0))
Вроде бы нигде не наврал:)
x_{n+k} + a_{k} * x_{n+k} +… + a_0 * x_{n} = 0 при n > 0.
(для чисел Фибоначчи: k = 2, x_0 = x_1 = 1, a_2 = a_1 = -1: x_{n+2} — x_{n+1} — x_{n} = 0, т.е. x_{n+2} = x_{n+1} + x_{n}).
Рассмотрим вектора y = (x_{n+k+1}, x_{n+k}, ..., x_{n+1}) и z = (x_{n+k},… x_{n}:
Замечаем, что можно выразить y через z линейно:
y_{k+1} = x_{n+k+1} = — a_{k} * x_{n+k} — … — a_0 * x_{n} = -a_{k} * z_{k+1} — … — a_0 * z_{1}
y_{k} = x_{n+k} = z_{k+1}
…
y_{1} = z_{2}
Получаем, что y = A*z, где A — искомая матрица. Ее можно выписать явно:
((-a_{k}, -a_{k-1}, ..., -a_{0}),
(1, 0, ..., 0),
(0, 1, ..., 0),
...,
(0, 0, ..., 1, 0))
Вроде бы нигде не наврал:)
Если хотите, могу еще написать как вывести общую формулу для n-го члена последовательности:)
Напишите, будет интересно.
Итак, нам нужно найти бесконечную последовательность, удовлетворяющую соотношению
x_{n+k} + a_{k} * x_{n+k} +… + a_0 * x_{n} = 0.
Заметим, что если {x_n} и {y_n} — две подходящих последовательности, то последовательность {x_n + y_n} и {a*x_n} — тоже подходящие, т.е. интересующие нас последовательности образуют линейное подпространство в пространстве всех последовательностей. Его размерность равна k+1, так как последовательность, с одной стороны, однозначно задается k числами {x_0, ..., x_k}, с другой — любым двум таким различным наборам чисел соответствуют различные последовательности.
Рассмотрим многочлен:
f(t) = t^{k+1} + a_k * t^{k} +… + a_0 = 0
Как известно из основной теоремы алгебры, у него ровно N корней с учетом кратности.
Пусть c — корень кратности s+1. Тогда для любых констант C0, ..., CS последовательность
x_k = (C0 + C1*k + C2*k^2 +… + CS*k^s) * c^k будет решением (т.е. произвольный многочлен P(k) степени не выше S, умноженный на c^k).
Докажем это, т.е. что
P(n+k+1)*c^{n+k+1} + a_k * P(n+k) * c^{n+k} +… + a_0 * P(n) * c^n = 0.
В силу линейности, достаточно рассматривать многочлены вида P(k) = k^i. Перейдем к такому случаю, и сократим на c^n:
(n+k+1)^i * c^{k+1} + a_k * (n+k)^i * c^{k} +… + a_0 * n^i = 0.
Разложим это по степеням n (и вынесем из каждой скобки c в максимально возможной степени):
n^i * (c^{k+1} + a_k * c^k +… + a_0) + i*n^{i-1} * c * ((k+1) * c^{k} + k * c^{k-1} +… + a_1) +… = 0
Из общей теории получаем, что, так как c — корень кратности s+1 многочлена f, то f© = f'© = f''© =… = f^(s) © = 0 (т.е. все производные, вплоть до s-й, равны нулю).
Запишем явно производный от f вплоть до s-й:
f^(0) = t^{k+1} + a_k * t^{k} +… + a_0
f^(1) = (k+1)*t^k + a_k * k * t^{k-1} +…
…
Замечаем, что эти производные в точности равны тому, что стоит в скобках в разложении, если в них вместо t подставить c. А так как c — это корень S-й степени, то все производные равны нулю, т.е. все скобки равны нулю, и вся сумма равна нулю, что и требовалось доказать.
Таким образом, каждый корень кратности S дает нам S независимых решений. Решения, соответствующие разным корням, тоже независимы, сумма всех кратностей равна N = > мы нашли все решения.
Для тех, кому лень было читать вывод — готовый алгоритм:
1. Ищем последовательность, удовлетворяющую уравнению x_{n+k} + a_{k} * x_{n+k} +… + a_0 * x_{n} = 0
2. Пишем характеристический многочлен: t^{k+1} + a_k * t^{k} +… + a_0
3. Находим корни характеристического многочлена, т.е. представляем его в виде (t-c1)^s1 * (t-c2)^s2 * ..., где все ci попарно различны.
4. Общий вид последовательность: x_n = (C1_0 + C1_1*n +… + C1_s1 * n^{s1-1})*c1^n + (C2_0 + C2_1*n +… + C2_s2 * n^{s2-1})*c2^n +…
5. Если у нас фиксировано начало — то подставляем в эту формулу n=0,1,...,k и находим все константы.
Например, для чисел Фибоначчи:
x_{n+2} — x_{n+1} — x_{n} = 0
t^2 — t — 1 = 0
D = 5
t = (1 +- sqrt(5)) / 2
x_n = A*((1+sqrt(5))/2)^n + B*((1-sqrt(5))/2)^n
Разным значениям A и B соответствуют разные значения первых двух членов.
x_0 = A+B
x_1 = A(1+sqrt(5))/2 + B(1-sqrt(5))/2
В стандартном случае x_0 = 0, x_1 = 1
A+B = 0
A*sqrt(5)/2 — B*sqrt(5)/2 = 1
A+B=0
A-B=2/sqrt(5)
A = 1/sqrt(5)
B = -1/sqrt(5)
(что соответствует формулам из вики:D)
В ветку призывается nsinreal, которому не лень переводить TeX-овские формулы в картинки.
x_{n+k} + a_{k} * x_{n+k} +… + a_0 * x_{n} = 0.
Заметим, что если {x_n} и {y_n} — две подходящих последовательности, то последовательность {x_n + y_n} и {a*x_n} — тоже подходящие, т.е. интересующие нас последовательности образуют линейное подпространство в пространстве всех последовательностей. Его размерность равна k+1, так как последовательность, с одной стороны, однозначно задается k числами {x_0, ..., x_k}, с другой — любым двум таким различным наборам чисел соответствуют различные последовательности.
Рассмотрим многочлен:
f(t) = t^{k+1} + a_k * t^{k} +… + a_0 = 0
Как известно из основной теоремы алгебры, у него ровно N корней с учетом кратности.
Пусть c — корень кратности s+1. Тогда для любых констант C0, ..., CS последовательность
x_k = (C0 + C1*k + C2*k^2 +… + CS*k^s) * c^k будет решением (т.е. произвольный многочлен P(k) степени не выше S, умноженный на c^k).
Докажем это, т.е. что
P(n+k+1)*c^{n+k+1} + a_k * P(n+k) * c^{n+k} +… + a_0 * P(n) * c^n = 0.
В силу линейности, достаточно рассматривать многочлены вида P(k) = k^i. Перейдем к такому случаю, и сократим на c^n:
(n+k+1)^i * c^{k+1} + a_k * (n+k)^i * c^{k} +… + a_0 * n^i = 0.
Разложим это по степеням n (и вынесем из каждой скобки c в максимально возможной степени):
n^i * (c^{k+1} + a_k * c^k +… + a_0) + i*n^{i-1} * c * ((k+1) * c^{k} + k * c^{k-1} +… + a_1) +… = 0
Из общей теории получаем, что, так как c — корень кратности s+1 многочлена f, то f© = f'© = f''© =… = f^(s) © = 0 (т.е. все производные, вплоть до s-й, равны нулю).
Запишем явно производный от f вплоть до s-й:
f^(0) = t^{k+1} + a_k * t^{k} +… + a_0
f^(1) = (k+1)*t^k + a_k * k * t^{k-1} +…
…
Замечаем, что эти производные в точности равны тому, что стоит в скобках в разложении, если в них вместо t подставить c. А так как c — это корень S-й степени, то все производные равны нулю, т.е. все скобки равны нулю, и вся сумма равна нулю, что и требовалось доказать.
Таким образом, каждый корень кратности S дает нам S независимых решений. Решения, соответствующие разным корням, тоже независимы, сумма всех кратностей равна N = > мы нашли все решения.
Для тех, кому лень было читать вывод — готовый алгоритм:
1. Ищем последовательность, удовлетворяющую уравнению x_{n+k} + a_{k} * x_{n+k} +… + a_0 * x_{n} = 0
2. Пишем характеристический многочлен: t^{k+1} + a_k * t^{k} +… + a_0
3. Находим корни характеристического многочлена, т.е. представляем его в виде (t-c1)^s1 * (t-c2)^s2 * ..., где все ci попарно различны.
4. Общий вид последовательность: x_n = (C1_0 + C1_1*n +… + C1_s1 * n^{s1-1})*c1^n + (C2_0 + C2_1*n +… + C2_s2 * n^{s2-1})*c2^n +…
5. Если у нас фиксировано начало — то подставляем в эту формулу n=0,1,...,k и находим все константы.
Например, для чисел Фибоначчи:
x_{n+2} — x_{n+1} — x_{n} = 0
t^2 — t — 1 = 0
D = 5
t = (1 +- sqrt(5)) / 2
x_n = A*((1+sqrt(5))/2)^n + B*((1-sqrt(5))/2)^n
Разным значениям A и B соответствуют разные значения первых двух членов.
x_0 = A+B
x_1 = A(1+sqrt(5))/2 + B(1-sqrt(5))/2
В стандартном случае x_0 = 0, x_1 = 1
A+B = 0
A*sqrt(5)/2 — B*sqrt(5)/2 = 1
A+B=0
A-B=2/sqrt(5)
A = 1/sqrt(5)
B = -1/sqrt(5)
(что соответствует формулам из вики:D)
В ветку призывается nsinreal, которому не лень переводить TeX-овские формулы в картинки.
Слушайте, ну там ничего сложно. Заходите сюда, пишете TeX-формулу, получаете ссылку, вставляете как рисунок
Да, еще есть некоторая наука о том, как решать системы вида
x_{n+k+1} + a_k*x_{n+k} +… + a_0*x_n = b_n, но там уже нужны чуть более злые вещи типа свертки.
x_{n+k+1} + a_k*x_{n+k} +… + a_0*x_n = b_n, но там уже нужны чуть более злые вещи типа свертки.
Откуда свертка-то?
Тут, как и в дифурах, достаточно найти решение для однородной последовательности (где в уравнении справа 0), а потом сложить с частным решением.
Свертки возникают в ситуациях со слагаемыми вида x_{n+a}*x_{n+b}
Тут, как и в дифурах, достаточно найти решение для однородной последовательности (где в уравнении справа 0), а потом сложить с частным решением.
Свертки возникают в ситуациях со слагаемыми вида x_{n+a}*x_{n+b}
А как найти частное решение?)
Вроде бы там получается, что если найдено быстро убывающее решение однородного, то можно что-то свернуть с правой частью и получается решение неоднородного… Не помню, а выводить лень. Приду домой — посмотрю в конспекте.
Вроде бы там получается, что если найдено быстро убывающее решение однородного, то можно что-то свернуть с правой частью и получается решение неоднородного… Не помню, а выводить лень. Приду домой — посмотрю в конспекте.
Опять таки, вид частного решения зависит от вида правой части.
Впрочем, да. Для правой части произвольного вида действительно получается свертка. Только вот эту свертку еще и вычислять придется, а это действие не самое простое. Считать же ее численно нет ни малейшего смысла: сложность свертки совпадает со сложностью исходной рекуррентной формулы.
Впрочем, да. Для правой части произвольного вида действительно получается свертка. Только вот эту свертку еще и вычислять придется, а это действие не самое простое. Считать же ее численно нет ни малейшего смысла: сложность свертки совпадает со сложностью исходной рекуррентной формулы.
Кусочек этого текста (пример), набранный в TeX.
Внутри картинки есть намёк всем, прочитавшим коммент mihaild
Внутри картинки есть намёк всем, прочитавшим коммент mihaild
Немного поправил верстку (а то совсем уродливо получается).
Ну вообще, я даже писал для этого программку просто потому что мне скучно было, да и интересно было, как можно «быстро» вычислить трибонначчи. Как оказалось, метод работает для всех линейно-реккурентных последовательностей и чуть больше (мой «алгоритм» позволяет также считать сумму последовательности).
Вообще, просто смотря на матрицу в статье вы не поймете почему и как это работает. Мне тогда потребовалось некоторое время, чтобы понять, что нужно зайти немного с другой стороны и посмотреть почему используется произведение. В итоге, я понял, что оригинальный метод таков: мы можем помножить однострочную матрицу с набором значений Fn на спец. матрицу Q, чтобы получился следующий набор значений. Т.е. матрица
(давайте назовем её изначальной матрицой) при умножении на Q превращается в матрицу 
. Осталось просто подобрать матрицу Q. Это легко сделать, понимая как работает умножение матриц. Давайте напишем это уравнение:
Матрица Q должна быть размера 2х2 (первое число — чтобы матрица была совместима с оригинальной для умножения, второе — чтобы получить конечную матрицу размера 2x1).
Распишем:
Отсюда получаем:
Поскольку F(n+1) = 0 + F(n+1), а F(n+2) = F(n) + F(n+1), то получаем, что матрица Q равна:
. Подобным образом легко выводится матрица для последовательности трибонначчи:
Таким образом нам нужно изначальную матрицу {0, 1} умножить n раз на Q, чтобы получить конечную {F(n), F(n+1)}. И вот тут у вас должен появиться вопрос — а куда собственно пропала начальные и конечная матрица и почему в статье они не описаны? А причина заключается в том, что так совпало, что если исключить из алгоритма изначальную матрицу ничто не поломается.
Потом, если мы хотим работать также с арифметической прогрессией или считать сумму, нам нужно всего-лишь чуть-чуть подумать как их туда запихнуть. Пускай у нас будет функция F(n)=F(n-1)+F(n-2)+d, а мы должны посчитать её сумму. Вот вам эта матрица:
Вообще, вам придется немного подумать и расписать умножение матриц. Не волнуйтесь, вы сможете все понять — это совсем не сложно — просто почитайте вики и поработайте ручкой. Мне потребовался день-два (с перерывами), чтобы получить метод. А я ведь по факту тогда вообще не понимал матрицы (один семестр ЛААГ не в счет, я все равно в итоге ничего из него не понял). Для того, чтобы объяснить метод вам нагляднее (на уровне школьника) потребуется писать целую статью и рисовать полноценные иллюстрации (а не мини-tex формулы) — а это не формат комментария.
Вот рабочий код на C#: исходник. Я надеюсь вы поймете код, я пытался его комментировать, но с английским и умением писать комментарии у меня пока нелады. Да, кстати, извините за метод вычисления матриц — кажется он неправильный (см. операцию mod %) — там может быть переполнение.
Вообще, просто смотря на матрицу в статье вы не поймете почему и как это работает. Мне тогда потребовалось некоторое время, чтобы понять, что нужно зайти немного с другой стороны и посмотреть почему используется произведение. В итоге, я понял, что оригинальный метод таков: мы можем помножить однострочную матрицу с набором значений Fn на спец. матрицу Q, чтобы получился следующий набор значений. Т.е. матрица
Матрица Q должна быть размера 2х2 (первое число — чтобы матрица была совместима с оригинальной для умножения, второе — чтобы получить конечную матрицу размера 2x1).
Распишем:
Отсюда получаем:
Поскольку F(n+1) = 0 + F(n+1), а F(n+2) = F(n) + F(n+1), то получаем, что матрица Q равна:
Таким образом нам нужно изначальную матрицу {0, 1} умножить n раз на Q, чтобы получить конечную {F(n), F(n+1)}. И вот тут у вас должен появиться вопрос — а куда собственно пропала начальные и конечная матрица и почему в статье они не описаны? А причина заключается в том, что так совпало, что если исключить из алгоритма изначальную матрицу ничто не поломается.
Потом, если мы хотим работать также с арифметической прогрессией или считать сумму, нам нужно всего-лишь чуть-чуть подумать как их туда запихнуть. Пускай у нас будет функция F(n)=F(n-1)+F(n-2)+d, а мы должны посчитать её сумму. Вот вам эта матрица:
Вообще, вам придется немного подумать и расписать умножение матриц. Не волнуйтесь, вы сможете все понять — это совсем не сложно — просто почитайте вики и поработайте ручкой. Мне потребовался день-два (с перерывами), чтобы получить метод. А я ведь по факту тогда вообще не понимал матрицы (один семестр ЛААГ не в счет, я все равно в итоге ничего из него не понял). Для того, чтобы объяснить метод вам нагляднее (на уровне школьника) потребуется писать целую статью и рисовать полноценные иллюстрации (а не мини-tex формулы) — а это не формат комментария.
Вот рабочий код на C#: исходник. Я надеюсь вы поймете код, я пытался его комментировать, но с английским и умением писать комментарии у меня пока нелады. Да, кстати, извините за метод вычисления матриц — кажется он неправильный (см. операцию mod %) — там может быть переполнение.
Да, код позволяет генерировать такие матрицы в автоматическом режиме для любых линейно-рекуррентных последовательностей и считать их сумму за O(M^3 * logN) для малых чисел или за O(M^3 * N) для длинной арифметики, M — кол-во членов входящих в правило для генерации
Я написал быстрее и короче, зато у Вас формулы с картинками и афинные последовательности, а не только линейные.
Посмотрим, чей вариант больше понравится сообществу)
Посмотрим, чей вариант больше понравится сообществу)
Да, для тех, кто удивится, что у нас с Вами получились немного разные матрицы: в моем варианте векторы-столбцы и координаты от большего номера к меньшему, в Вашем — строки и от меньшего к большему:)
Э… это вообще-то есть в любой книге по линейной алгебре для первого курса университета.
Не в любой. И у нас (мехмат МГУ) этого в обязательной программе по линалу не было (на семинарах рассказывали, но это была чисто инициатива семинариста). А было это в программе ЧМов.
Что же говорить о тех людях, у которых линейка читается один семестр и то для галочки и зачета. Кстати, а как у вас было, линейна алгебра и аналитическая геометрия — это один предмет?
Нет, у нас в 1м семестре был ангем, во 2м — линал. На котором изучалось примерно то же самое, но в более общем виде. Еще в ангеме были основы проективки, в линале вроде бы нет. Зато были в дифгеме.
«То же самое, в более общем виде» — это преувеличение. Можно сказать, что в линалгебре нам показали механизм, которым мы пользовались полгода назад для трехмерного случая. Но и в ангеме было много своей специфике, и в линейке много того, что в ангеме не требовалось вообще. Проективка каким-то образом попала в теорию групп и колец :) но ее было очень мало.
Кстати, а какие области математики вы бы посоветовали для самостоятельного изучения для программистов как полезные?
Для каких программистов? Могу сказать, что для моей нынешней деятельности (обработка сигналов+компьютерная геометрия) полезен был весь курс мехмата. Хотя непосредственного применения теории меры и функана я не наблюдаю, они все равно не мешают. Остальное в той или иной мере используется.
Если хочется практического применения — то основы матана и линейной алгебры для подготовки фундамента (ряды Фурье еще нужны, дифференциальные формы уже вряд ли), потом теория вероятностей, диффуры (самые основы, без разбора доказательств), и, разумеется, численные методы. И линейное программирование. Дифференциальную геометрию и УРЧП надо иметь в виду, но они пригодятся с вероятностью 5%, не более.
А можно сразу начать с численных методов. Читать как художественную литературу, причем не один раз. Если вопросы вознкнут, пойти искать их в более фундаментальных предметах, но без фундамента это будет тяжело.
Если хочется практического применения — то основы матана и линейной алгебры для подготовки фундамента (ряды Фурье еще нужны, дифференциальные формы уже вряд ли), потом теория вероятностей, диффуры (самые основы, без разбора доказательств), и, разумеется, численные методы. И линейное программирование. Дифференциальную геометрию и УРЧП надо иметь в виду, но они пригодятся с вероятностью 5%, не более.
А можно сразу начать с численных методов. Читать как художественную литературу, причем не один раз. Если вопросы вознкнут, пойти искать их в более фундаментальных предметах, но без фундамента это будет тяжело.
Так, по порядку: где Вам были нужны теория групп? матлог (в том виде, в котором его дают в основном курсе, т.е. основы классической логики и немного общих слов о теоремах Гёдедя)? интеграл Лебега (и при этом не хватает интеграла Римана)? абстрактные многообразия? когомологии? вся эта бесконечная теория со слупами? всякие там дзета-функции и характеры Дирихле?
Вопрос не в том, зачем они нужны — «математики не отвечают на вопрос „зачем“», вопрос — где они используются на практике?
Вопрос не в том, зачем они нужны — «математики не отвечают на вопрос „зачем“», вопрос — где они используются на практике?
По порядку.
Теория групп:
— Работа с группой вращений и перемещений пространства; представление группы вращений через кватернионы; переходы между кватернионным и матричным представлениями. Можно, конечно, это назвать линейной алгеброй — но здесь она смыкается с теорией групп.
— Конечные группы. Использовал, скорее, для развлечения (игрушка — реализация многомерных многогранников Рубика), но там теорию групп пришлось применять вовсю.
Матлогика:
— Представление о структуре булевых функций, разложение по базисам, оптимизация формул — используется довольно часто.
— Машина Тьюринга — была вторым компьютером, на котором я работал (после БЗ-34), так что использовалась для обучения программированию и понятию алгоритма вообще (и навыкам микрооптимизации кода)
— Теоремы Геделя, пожалуй, не используются.
Интеграл Лебега:
— Там же, где и теория меры (я написал, что непосредственного применения нет). Используется для тренировки воображения.
Абстрактные многообразия:
— В целом — для нелинейных многопараметрических оптимизаций. При калибровке геометрических параметров сканера приходится рассматривать и его многообразие его возможных состояний, и результат их воздействия на пространство (получается примерно 20-мерное многообразие в 3N-мерном пространстве, где N порядка 100), и дальше поиск ближайших точек, оценка якобианов преобразований и т.п. Фактически, мое основное занятие в последнее время.
«когомологии? вся эта бесконечная теория со слупами»
— В основном курсе я такого не помню.
Дзета-функции и характеры
— криптографией я не занимаюсь, поэтому в чистом виде ими не пользуюсь, но вообще теория конечных полей периодически всплывает (начиная с китайской теоремы об остатках). Доказательство транцедентности числа «пи» использовать пока не приходилось, но алгебраические числа регулярно всплывают (правда, опять в игрушках — в моду входят головоломки в пространстве Лобачевского).
Теория групп:
— Работа с группой вращений и перемещений пространства; представление группы вращений через кватернионы; переходы между кватернионным и матричным представлениями. Можно, конечно, это назвать линейной алгеброй — но здесь она смыкается с теорией групп.
— Конечные группы. Использовал, скорее, для развлечения (игрушка — реализация многомерных многогранников Рубика), но там теорию групп пришлось применять вовсю.
Матлогика:
— Представление о структуре булевых функций, разложение по базисам, оптимизация формул — используется довольно часто.
— Машина Тьюринга — была вторым компьютером, на котором я работал (после БЗ-34), так что использовалась для обучения программированию и понятию алгоритма вообще (и навыкам микрооптимизации кода)
— Теоремы Геделя, пожалуй, не используются.
Интеграл Лебега:
— Там же, где и теория меры (я написал, что непосредственного применения нет). Используется для тренировки воображения.
Абстрактные многообразия:
— В целом — для нелинейных многопараметрических оптимизаций. При калибровке геометрических параметров сканера приходится рассматривать и его многообразие его возможных состояний, и результат их воздействия на пространство (получается примерно 20-мерное многообразие в 3N-мерном пространстве, где N порядка 100), и дальше поиск ближайших точек, оценка якобианов преобразований и т.п. Фактически, мое основное занятие в последнее время.
«когомологии? вся эта бесконечная теория со слупами»
— В основном курсе я такого не помню.
Дзета-функции и характеры
— криптографией я не занимаюсь, поэтому в чистом виде ими не пользуюсь, но вообще теория конечных полей периодически всплывает (начиная с китайской теоремы об остатках). Доказательство транцедентности числа «пи» использовать пока не приходилось, но алгебраические числа регулярно всплывают (правда, опять в игрушках — в моду входят головоломки в пространстве Лобачевского).
Для работы с группой вращений и кватернионами нужно что-то, кроме определения группы? Там используются понятия классов смежности, факторгруппы, коммутаторы, теоремы Силова и т.д.?
Структура булевых функций и формулы — это скорее ТДФ, чем матлог.
МТ занимает очень небольшую часть курса (Беклемишев вроде бы ее даже вводил за одну или две лекции до конца). Основная часть курса матлога — это исчисления высказываний и предикатов, теоремы о повышении и понижении мощности и т.д.
Вы используете именно абстрактную структуру — атласы, касательные вектора как операторы дифференцирования и т.д., или всё же конкретную, получающуюся вложением в R^n (если что, про теорему Уитни я помню).
Когомологии изучаются в 5м семестре в дифгеме. Собственно, он состоит из двух больших разделов: тензоры и дифференциальные формы, и гомотопии и когомологии (оттуда уже не помню ничего, кроме теоремы о причесывании ежа).
Слупы — 3й предмет курса тервера, читается в 6м семестре.
Я специально не написал «ТЧ вообще», а указал конкретные пункты:) Китайская теорема об остатках и вообще конечные поля изучаются в общем курсе на пальцах. Я про более сложные вещи, где возникают странные неожиданные переходы от простых чисел к интегралам и подобное.
Структура булевых функций и формулы — это скорее ТДФ, чем матлог.
МТ занимает очень небольшую часть курса (Беклемишев вроде бы ее даже вводил за одну или две лекции до конца). Основная часть курса матлога — это исчисления высказываний и предикатов, теоремы о повышении и понижении мощности и т.д.
Вы используете именно абстрактную структуру — атласы, касательные вектора как операторы дифференцирования и т.д., или всё же конкретную, получающуюся вложением в R^n (если что, про теорему Уитни я помню).
Когомологии изучаются в 5м семестре в дифгеме. Собственно, он состоит из двух больших разделов: тензоры и дифференциальные формы, и гомотопии и когомологии (оттуда уже не помню ничего, кроме теоремы о причесывании ежа).
Слупы — 3й предмет курса тервера, читается в 6м семестре.
Я специально не написал «ТЧ вообще», а указал конкретные пункты:) Китайская теорема об остатках и вообще конечные поля изучаются в общем курсе на пальцах. Я про более сложные вещи, где возникают странные неожиданные переходы от простых чисел к интегралам и подобное.
Во-первых, используется сам формализм работы в некоммутативных кольцах. Коммутаторы встречаются, сопряженные элементы — просто основной механизм. Классы смежности — сходу не скажу, но когда они мне понадобятся, воспользуюсь, не раздумывая. Теорема Силова относится к конечным группам, и в SO3 не нужна.
Классы булевых функций у нас занимали больше половины курса (лекции читал Лупанов). Теорема о полноте, предполные классы, и т.п. На практике применяются редко. А Беклемишев лекции не читал, он их слушал (если речь про Лёву).
Атласы и многократные покрытия использовать приходится. Но это отображение двумерного тора на сферу. Ну, и нетривиальные метрики (без явных расчетов вложения) там же.
Нет, стыковка ТЧ с ТФКП еще не требовалась. Контурные интегралы бывают, но крайне редко (и обычно используются для аналогии, чтобы понять, как придать какой-нибудь задаче математическую формулировку).
А когда я говорил про «весь курс мехмата», то имелась в виду не каждая глава каждого предмета, а, скорее, каждый предмет — в большей или меньшей степени. Но ведь заранее никогда не знаешь, что может пригодиться. И если пригодилось 30% от курса — то надо жалеть не о потраченном зря времени на остальные 70%, а о том, что мало изучил — слишком высоки шансы, что где-то рядом было еще что-то, что могло бы пригодиться.
Классы булевых функций у нас занимали больше половины курса (лекции читал Лупанов). Теорема о полноте, предполные классы, и т.п. На практике применяются редко. А Беклемишев лекции не читал, он их слушал (если речь про Лёву).
Атласы и многократные покрытия использовать приходится. Но это отображение двумерного тора на сферу. Ну, и нетривиальные метрики (без явных расчетов вложения) там же.
Нет, стыковка ТЧ с ТФКП еще не требовалась. Контурные интегралы бывают, но крайне редко (и обычно используются для аналогии, чтобы понять, как придать какой-нибудь задаче математическую формулировку).
А когда я говорил про «весь курс мехмата», то имелась в виду не каждая глава каждого предмета, а, скорее, каждый предмет — в большей или меньшей степени. Но ведь заранее никогда не знаешь, что может пригодиться. И если пригодилось 30% от курса — то надо жалеть не о потраченном зря времени на остальные 70%, а о том, что мало изучил — слишком высоки шансы, что где-то рядом было еще что-то, что могло бы пригодиться.
Хм, а у Вас были отдельные курсы ТДФ и матлога, или нет? (вроде кто-то говорил, что это недавнее изобретение)
Да, я забыл перенести теоремы Силова в следующий абзац, перепутал.
За рассказ об использовании — спасибо, интересно. Но вообще по ощущениям в основном курсе много частностей, которые можно было бы заменить единым более мощным средством (например, в функане вообще ничего не говорят про банаховы алгебры, хотя они во многих случаях из курса давали бы хорошее обобщение).
Да, я забыл перенести теоремы Силова в следующий абзац, перепутал.
За рассказ об использовании — спасибо, интересно. Но вообще по ощущениям в основном курсе много частностей, которые можно было бы заменить единым более мощным средством (например, в функане вообще ничего не говорят про банаховы алгебры, хотя они во многих случаях из курса давали бы хорошее обобщение).
У нас был один курс «мат.логика» (один семестр), и на нашем потоке его вела кафедра дискретной математики. Поэтому мы хорошо знали теорию булевых функций и почти не разбирались в исчислении предикатов.
Теорема Силова сама по себе у меня не использовалась. Разве что отдаленные намеки на нее, когда требовалось найти порождающий элемент мультипликативной группы конечного поля (а это бывало).
Теорема Силова сама по себе у меня не использовалась. Разве что отдаленные намеки на нее, когда требовалось найти порождающий элемент мультипликативной группы конечного поля (а это бывало).
В фундамент еще запишите матлогику :) Куда же без нее :)
И многие разделы дискретной математики еще, пожалуй )
Если уж на то пошло, то метод обобщается вообще на любые линейные преобразования набора переменных.
Например, на динамику по профилю — строим матрицу переходов и возводим её в степень.
Например, на динамику по профилю — строим матрицу переходов и возводим её в степень.
Обычный стандартный алгоритм, не достоин отдельной статьи. К тому же описали вы банальные вещи.
Вот вам ещё короче версия O(log N) по модулю M (использует рекуррентные формулы)
Вот вам ещё короче версия O(log N) по модулю M (использует рекуррентные формулы)
typedef unsigned long long uint64;
uint64 fib_mod_m (uint64 n, uint64 m)
{
uint64 x = 1, y = 0, xx, t;
if (n <= 1)
return n;
int b = 62 - __builtin_clzll(n);
for (; b >= 0; b--)
{
xx = (x * x) % m;
x = (xx + 2 * x * y) % m;
y = (xx + y * y) % m;
if ((n << (63 - b)) >> 63)
{
t = x;
x = (x + y) % m;
y = t;
}
}
return x;
}
Ну, это то же самое, только матричное умножение явно расписано) И некая магия с битовыми сдвигами, которая вроде бы не обобщается на длинную арифметику.
А так — да, алгоритм стандартный)
А так — да, алгоритм стандартный)
Насколько я понял битовая магия просто напросто проверяет, будет ли переполнение, и если да — то обрезает число. Не факт, что обрезает правильно. Вообще, я правда магию не понял, так что не факт, что оно делает то, что я написал.
«Магия» проверяет, чему равен b-й бит числа. Можно было бы написать (n>>b)&1. Или сохранить n1=n<<(62-b1) — перед циклом — и каждый раз в цикле проверять if(n1<0)… и сдвигать n1 на 1 разряд вправо. На машинах, где скорость сдвигов зависит от длины сдвига (вроде старых 8086) получится быстрее.
В случае длинной арифметики либо пишем (n[b>>5]>>(b&31))&1, либо конструируем двойной цикл.
В случае длинной арифметики либо пишем (n[b>>5]>>(b&31))&1, либо конструируем двойной цикл.
Кстати, это немного другой вариант формулы. Кажется я его в SICPе видел, но так и не понял, как это выводится (может, не особо старался)
Да, это я слишком уж мельком посмотрел. Алгоритм довольно сильно другой, и не очень понятно, как он получается.
VladX, можете подсказать? Спасибо.
VladX, можете подсказать? Спасибо.
Там используются формулы для чётного и нечётного N, вроде бы в википедии есть эти формулы. Они, насколько я помню, получаются из матричных. Я где-то видел хорошую публикацию на эту тему, там неплохо разжеваны все формулы и свойства последовательности Фибоначчи, попробую найти.
Меня все-таки интересует полноценное объяснение с возможностью применения для всех линейно-рекуррентных функций. Ну т.е. чтобы был хотя-бы намек как такие формулы генерировать. Или проще тупо через матрицы считать?
Ну это уже отдельная большая тема. Вообще да, «проще тупо через матрицы считать». Обобщить просто так не получится, нужно каждый раз выводить эти формулы для разных рекуррентных функций. Более точно сказать не могу, ибо не обладаю достаточным уровнем математической подготовки. Если бы мне нужно было считать для любых линейно-рекуррентных функций, я бы юзал матричный способ.
Намеки есть. Но способ довольно трудоемкий, и даже проверять его нет времени.
Рассмотрим на примере чисел трибоначчи.
Мы знаем, что a[n]+a[n+1]+a[n+2]-a[n+3]=0.
Будем искать формулы для a[2n] и a[2n+1] в виде
a[2n]=M0(a[n],a[n+1],a[n+2]) и a[2n+1]=M1(a[n]+a[n+1]+a[n+2]),
где M0 и M1 — квадратичные формы:
M0(p,q,r)=m00*p^2+2*m01*p*q+2*m02*p*r+m03*q^2+2*m04*q*r+m05*r^2,
с M1 — аналогично.
Теперь запишем условия
M0(p,q,r)+M1(p,q,r)+M0(q,r,p+q+r)-M1(q,r,p+q+r)=0
и
M1(r-p-q,p,q)+M0(p,q,r)+M1(p,q,r)-M0(q,r,p+q+r)=0
в каждом из них сгруппируем слагаемые с p^2, p*q, p*r и т.д. и приравняем коэффициенты при них нулю. Получится система из 12 уравнений на 12 неизвестных, но она однородная, и я подозреваю, что ее ранг будет равен 10 или 9. Чтобы найти конкретные значения коэффициентов, надо будет добавить условия M0(0,1,1)=0, M1(0,1,1)=1, M0(1,1,1)=1 (чтобы показать, откуда мы начинаем последовательность).
С хорошей вероятностью результат получится. Но я не проверял.
Рассмотрим на примере чисел трибоначчи.
Мы знаем, что a[n]+a[n+1]+a[n+2]-a[n+3]=0.
Будем искать формулы для a[2n] и a[2n+1] в виде
a[2n]=M0(a[n],a[n+1],a[n+2]) и a[2n+1]=M1(a[n]+a[n+1]+a[n+2]),
где M0 и M1 — квадратичные формы:
M0(p,q,r)=m00*p^2+2*m01*p*q+2*m02*p*r+m03*q^2+2*m04*q*r+m05*r^2,
с M1 — аналогично.
Теперь запишем условия
M0(p,q,r)+M1(p,q,r)+M0(q,r,p+q+r)-M1(q,r,p+q+r)=0
и
M1(r-p-q,p,q)+M0(p,q,r)+M1(p,q,r)-M0(q,r,p+q+r)=0
в каждом из них сгруппируем слагаемые с p^2, p*q, p*r и т.д. и приравняем коэффициенты при них нулю. Получится система из 12 уравнений на 12 неизвестных, но она однородная, и я подозреваю, что ее ранг будет равен 10 или 9. Чтобы найти конкретные значения коэффициентов, надо будет добавить условия M0(0,1,1)=0, M1(0,1,1)=1, M0(1,1,1)=1 (чтобы показать, откуда мы начинаем последовательность).
С хорошей вероятностью результат получится. Но я не проверял.
поправка: a[2n+1]=M1(a[n],a[n+1],a[n+2]).
Чтобы найти конкретные значения коэффициентов, надо будет добавить условия M0(0,1,1)=0, M1(0,1,1)=1, M0(1,1,1)=1 (чтобы показать, откуда мы начинаем последовательность).
О как. Т.е. мы задаем начальные члены и не можем на лету получить 10 значений T(n) для разных начальных членов? (Когда мы считаем степень матрицы Q, мы потом умножаем её на изначальную матрицу слева. Можно умножить её на матрицы {0,0,1}, {1,2,3}, {-1,10,9} — т.е. с разными начальными данными)
Да, можно и так. Запишем уравнения
M0(0,1,1)=0
M1(0,1,1)=1
M0(1,1,1)=1
M1(1,1,1)=1
M0(1,1,3)=3
M1(1,1,3)=5
и т.д. — всего 12 штук — и сразу найдем все 12 коэффициентов матриц. И рекуррентную формулу знать даже не нужно — достаточно, что она содержит 3 слагаемых и однородна.
Так даже проще.
M0(0,1,1)=0
M1(0,1,1)=1
M0(1,1,1)=1
M1(1,1,1)=1
M0(1,1,3)=3
M1(1,1,3)=5
и т.д. — всего 12 штук — и сразу найдем все 12 коэффициентов матриц. И рекуррентную формулу знать даже не нужно — достаточно, что она содержит 3 слагаемых и однородна.
Так даже проще.
Я правильно понимаю, что эта операция примерно соответствует приведению порождающей матрицы к ЖНФ?
Не думаю. Приведение к ЖНФ — это как раз получение нерекуррентной формулы через корни характеристического многочлена. А эта операция — не более, чем черная магия (или грязный хак, если угодно). Потому что без доказательства корректности. Зато работает :)
Да, я что-то протупил.
Общее утверждение, видимо, имеет вид «x_{2*n+c} есть квадратичная форма от x_{n-k}, ..., x_{n+l}» при некоторых ограничениях на c, k и l.
Это выглядит вполне разумно: x_{2*n+c} есть какой-то элемент A^{2*n}*X0, а x_{n-k}, ..., x_{n+l} есть элементы A^{n}*X0. Так как элементы A^2 есть квадратичные формы от элементов A, то в такое утверждение можно поверить.
Общее утверждение, видимо, имеет вид «x_{2*n+c} есть квадратичная форма от x_{n-k}, ..., x_{n+l}» при некоторых ограничениях на c, k и l.
Это выглядит вполне разумно: x_{2*n+c} есть какой-то элемент A^{2*n}*X0, а x_{n-k}, ..., x_{n+l} есть элементы A^{n}*X0. Так как элементы A^2 есть квадратичные формы от элементов A, то в такое утверждение можно поверить.
Сразу получается:
T[2*n]=T[n]*(2*T[n+2]-2*T[n+1]-T[n])+T[n+1]^2
T[2*n+1]=T[n]^2-T[n+1]^2+2*T[n+1]*T[n+2]
(если считать T[0]=T[1]=0,T[2]=1).
Мои предыдущие формулы неправильны. Должно быть так:
M0(0,0,1)=0
M1(0,0,1)=0
M0(0,1,1)=1
M1(0,1,1)=1
M0(1,1,2)=2
M1(1,1,2)=4
и т.д.
T[2*n]=T[n]*(2*T[n+2]-2*T[n+1]-T[n])+T[n+1]^2
T[2*n+1]=T[n]^2-T[n+1]^2+2*T[n+1]*T[n+2]
(если считать T[0]=T[1]=0,T[2]=1).
Мои предыдущие формулы неправильны. Должно быть так:
M0(0,0,1)=0
M1(0,0,1)=0
M0(0,1,1)=1
M1(0,1,1)=1
M0(1,1,2)=2
M1(1,1,2)=4
и т.д.
По поводу битовой магии: она там просто для явного подсчёта количества шагов алгоритма. Сам по себе алгоритм простейший — обычный метод Дихотомии (последовательного деления на 2).
Вот эта строчка
эквивалентна
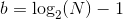
Вот эта строчка
int b = 62 - __builtin_clzll(n);
эквивалентна
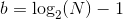
О вычислении чисел Фибоначчи на Хабре пишут с такой завидной настойчивостью, что давно уже пора переходить на примеры посложнее.
«Проще» — очень субъективное понятие. Мне проще написать нерекурсивный цикл:
Здесь содержательных — две строчки. И работает быстрее, потому что без рекурсии.
int mypow(Mat a, int b) {
Mat res;
for (; b; b >>= 1, a *= a)
if (b & 1) res *= a;
return res;
}
Здесь содержательных — две строчки. И работает быстрее, потому что без рекурсии.
Вообще-то нет. Рекурсивный вариант действительно проще в смысле понимания. я лично совершенно не понимаю как работает этот код. Не, сейчас уже понимаю, но несколько минут я только втыкал на код. Ой нет, опять не понимаю. Слушайте, а у вас res при создании чему равно?
Ну тут опять используется битовые операции. Про которые все нормальные современные компиляторы вроде бы уже давно в курсе, т.е. эти оптимизации не очень актуальны.
В более нормальном виде нерекурсивный вариант выглядит так:
В более нормальном виде нерекурсивный вариант выглядит так:
>>> def pow(a, b):
... res = 1
... while b:
... if b % 2:
... res *= a
... a *= a
... b /= 2
... return res
Нет, он все равно непонятен с первого взгляда. Тут необходимо знать что такое инвариант цикла и какой инвариант в вашем коде. Я думаю что-то типа такого должно быть более понятно:
def pow(a,b):
res = 1
starta = a
while b:
if b % 2 == 1 :
res *= starta
a *= a
b /= 2
res *= a
return res
Расставьте отступы правильно:) А то в таком варианте оно точно не работает. (и я не очень понимаю, как тут расставить отступы чтобы заработало)
ой… Так вот кажется, правда я питон не знаю
def pow(a,b):
res = 1
starta = a
while b:
if b % 2 == 1 :
res *= starta
a *= a
b /= 2
res *= a
return res
Не работает. Ответ получается вида a^O(log(b)) + a^{2^k}, где 2^k — наименьшая степень 2, большая b. Что очевидный абсурд.
Не сумма, а произведение. Но все равно неправильно.
Извините. Вот так, C#:
static int fastpow(int number, int exp) {
int res = 1;
int startnumber = number;
while ( exp != 0) {
if ( exp % 2 == 1 ) {
res *= startnumber;
exp--;
}
else {
number *= number;
exp /= 2;
}
}
res *= number;
return res;
}
Ну и снова — мы умножаем на startnumber порядка O(logN) раз, а в number оказывается startnumber^{2^k}. Т.е. получаем ответ вида number^(2^k + O(log N)).
Ну вы поняли, да?
Нет, не понял. Я не могу придумать, куда деть startnumber.
Мои фейлы — это самая прекрасна иллюстрация к моему тексту:
Рекурсивный вариант действительно проще в смысле понимания
Последняя попытка (чтобы вы не думали, что я вообще не способен написать итеративный вариант быстрого умножения):
static int fastpow(int number, int exp) {
// oddAcc * evenAcc ^ exp = result
int oddAcc = 1;
int evenAcc = number;
while ( exp != 1 ) {
if ( exp % 2 == 0 ) {
evenAcc = evenAcc * evenAcc;
exp/=2;
}
else {
oddAcc = oddAcc * evenAcc;
exp--;
}
}
return oddAcc * evenAcc;
}
Кстати, сейчас только заметил — у нас получился по-факту одинаковый код, за исключением того, что я явно выделил evenAcc. У вас в качестве evenAcc выступает входной аргумент. Ничего страшного, но кажется для классов в C# не прокатит.
При exp == 0 зависает, а так всё нормально вроде:)
А что, в C# нельзя написать так:
int blablabla(MyClass a) {
a = foo();
}
?
(в питоне можно, при этом то, что передавалось в качестве параметра не изменится)
А что, в C# нельзя написать так:
int blablabla(MyClass a) {
a = foo();
}
?
(в питоне можно, при этом то, что передавалось в качестве параметра не изменится)
>При exp == 0 зависает, а так всё нормально вроде:)
Знаю, я убрал лишние случаи, проверки и кидание эксепшенов из кода.
Не-не, я имел в виду, если у нас некоторые методы определены как нестатические (т.е. вызываются как a.Mult(..)), то это повредит оригинал. Ну да это мелочь, скорее всего когда будет переписывать на самописные матрицы, это заметят.
Знаю, я убрал лишние случаи, проверки и кидание эксепшенов из кода.
Не-не, я имел в виду, если у нас некоторые методы определены как нестатические (т.е. вызываются как a.Mult(..)), то это повредит оригинал. Ну да это мелочь, скорее всего когда будет переписывать на самописные матрицы, это заметят.
Почему же? Инвариант — answer = res*(a^b). В начале выполняется, при переходах тоже (т.к. res*(a^b)=(res*(a^(b%2))*((a^2)^(b/2). В конце b=0. Так что все чисто. А чтобы инвариант был виден, лучший способ — написать его в комментариях. Правда, это поможет только тем, кто понимает, что такое инвариант.
Вот видите — для того, чтобы понять рекурсивный способ нужно капелька ума и быстрый взгляд, а итеративный — понимание инварианта и знание, какой там должен быть инвариант
Чтобы понять рекурсивный способ — надо понять рекурсивный способ.
Расскажите, пожалуйста, что именно в процессе понимания бинарного возведения в степень заставляет вас изобретать инвариант цикла?
Т.е. вы хотите сказать, что при попытке понять итеративную версию вы не приходите к чему-то похожему на инвариант? Или вы имели в виду, что инвариант цикла должен писаться в комментариях?
Тут есть разница — понять реализацию или понять само «бинарное возведение в степень». В первом случае, без изобретения инварианта можно обойтись при трех условиях:
— алгоритм действительно должен выполнять возведение в степень
— вы в этом уверены
— в алгоритме есть ошибки.
В других ситуациях — например, алгоритм похож на бинарное возведение в степень, но делает что-то слегка другое (a^(b+2^k), или c*a^b, или a^b для нечетных b, а для четных неизвестно что), и в программе не написано, что он делает, но активно используется — там подобрать инвариант цикла будет полезно.
А во втором случае можно и обойтись. Перебираем биты b и умножаем аккумулятор на a^(2^k) — что делалось тут во многих примерах — и зачем инвариант? Работать будет и так.
— алгоритм действительно должен выполнять возведение в степень
— вы в этом уверены
— в алгоритме есть ошибки.
В других ситуациях — например, алгоритм похож на бинарное возведение в степень, но делает что-то слегка другое (a^(b+2^k), или c*a^b, или a^b для нечетных b, а для четных неизвестно что), и в программе не написано, что он делает, но активно используется — там подобрать инвариант цикла будет полезно.
А во втором случае можно и обойтись. Перебираем биты b и умножаем аккумулятор на a^(2^k) — что делалось тут во многих примерах — и зачем инвариант? Работать будет и так.
Единичная матрица должна получиться по дефолту. Ну, или нулевая. Смотря для чего класс Mat написан. Если для преобразований, то точно единичная.
Имел ввиду «мне проще написать и не набагать». Другое дело, что это я вбиваю скорее спинным мозгом, так что получается дело привычки.
В смысле читаемости и понятности спорить не буду — рекурсивный кажется понятнее.
В смысле читаемости и понятности спорить не буду — рекурсивный кажется понятнее.
В стандарте C++ не прописано, что хвостовая рекурсия должна оптимизироваться. Обычная рекурсия требует затрат памяти
Например, вот. 3*10^5 возведений матрицы 3x3 рекурсивным методом отработали за 790 мс, а нерекурсивным — за 630. Ускорение на 20%, что очень прилично.
Разумеется, при больших размерах матриц отношение уменьшится, но в случае тех же чисел Фибоначчи/Трибоначчи выигрыш существенен.
Разумеется, при больших размерах матриц отношение уменьшится, но в случае тех же чисел Фибоначчи/Трибоначчи выигрыш существенен.
У Вас неудачная реализация рекурсивного варианта.
Вот так:
оно работает за 1.42 против 1.7 с O3 и 1.26 против 3.27 с O2. (3 млн. шагов, матрицы 3х3)
Вот так:
Mat pow2(const Mat &a, int b) {
if (b == 0) {
return Mat();
}
Mat res = pow2(a, b / 2);
if (b % 2) {
res *= a;
}
return res;
}
оно работает за 1.42 против 1.7 с O3 и 1.26 против 3.27 с O2. (3 млн. шагов, матрицы 3х3)
У Вашей реализации есть один существенный недостаток — она выдаёт неверный ответ уже при b=2.
Вы забыли строчку
После рекурсивного вызова. Сейчас у вас считается что-то в стиле a^popcount(b).
Исправил. 0.910 vs 1.470.
Вы забыли строчку
res *= res;
После рекурсивного вызова. Сейчас у вас считается что-то в стиле a^popcount(b).
Исправил. 0.910 vs 1.470.
Рекурсивный вариант тоже имеет 2 содержательных строчки, причем они проще:
А еще можно понадеяться на то, что компилировать это будут gcc со включенной оптимизацией и написать
T pow(T a, int n) {
T tmp = n ? pow(a, n/2) : T(1);
return tmp*tmp*(n % 2 ? a : T(1));
}
А еще можно понадеяться на то, что компилировать это будут gcc со включенной оптимизацией и написать
int pow(int a, int n) {
return n ? (pow(a, n/2) * pow(a, n/2) * (n % 2 ? a : 1)) : 1;
}
Позволю себе процитировать yeputons:
«Проще» — очень субъективное понятие. Мне проще написать нерекурсивный цикл...
Если оптимизация нужна для устранения двух вычислений pow, то можно обойтись и без нее:
Если битовые операции не нравятся, n&2 меняется на n>1.
int pow(int a,int n){
return (n>3 ? pow(pow(a,n/2),2) : (n&2) ? a*a : 1))*(n%2 ? a : 1);
}
Если битовые операции не нравятся, n&2 меняется на n>1.
Автор заинтриговал, перед тем как полезть под кат решил по своему. Без книг.
1. Изучая последовательность с обратной стороны вывел формулу что F(n) = F(m+1)*F(n-m) + F(m)*F(n-m-1).
2. Т.е. уменьшить порядок чисел вдвое нужно = m=n/2 и для четных и нечетных формула примет вид:
Для нечетных F(n) = F(n/2-1)^2 + F(n/2)^2
Для четных F(n) = F(n/2) * (F(n/2) + 2*F(n/2-1))
Для четных формула адаптирована, чтобы при каждй итерации на выходе получались соседи как для четной так и дял нечетной формул (напрмиер F(723) -> F(367), F(366) а для них полчаем достаточную для рассчетов пару F(183) и F(182) и т.д. полчаем только 2х соседей)
Соответвенно спускаесмся за lg(n) шагов к F(1) и F(2)и попутно заносим, скажем в битовый массив, какой из 2х возможных формул пользовались при разложении (размер массива тоже lg(n)), потом в обратном порядке за те же lg(n) шагов полчаем нужное число.
Хорошая задачка.
1. Изучая последовательность с обратной стороны вывел формулу что F(n) = F(m+1)*F(n-m) + F(m)*F(n-m-1).
2. Т.е. уменьшить порядок чисел вдвое нужно = m=n/2 и для четных и нечетных формула примет вид:
Для нечетных F(n) = F(n/2-1)^2 + F(n/2)^2
Для четных F(n) = F(n/2) * (F(n/2) + 2*F(n/2-1))
Для четных формула адаптирована, чтобы при каждй итерации на выходе получались соседи как для четной так и дял нечетной формул (напрмиер F(723) -> F(367), F(366) а для них полчаем достаточную для рассчетов пару F(183) и F(182) и т.д. полчаем только 2х соседей)
Соответвенно спускаесмся за lg(n) шагов к F(1) и F(2)и попутно заносим, скажем в битовый массив, какой из 2х возможных формул пользовались при разложении (размер массива тоже lg(n)), потом в обратном порядке за те же lg(n) шагов полчаем нужное число.
Хорошая задачка.
А забыл, можно конечно же рекурсией воспользоваться (просто для меня это антипаттерн)
С такими формулами можно и снизу идти — полностью аналогично возведению в степень через двоичную запись:
void MulFib(double &a0,double &a1,double b0,double b1){
double c=a1*b1+a0*b0;
a0=a1*b0+a0*(b1-b0);
a1=c;
}
double NthFib(int n){
double a0=1,a1=1,b0=0,b1=1;
for(;n;n>>=1){
if(n&1) MulFib(b0,b1,a0,a1);
MulFib(a0,a1,a0,a1);
}
return b0;
}
какие красивые формулы у вас…
Зарегистрируйтесь на Хабре, чтобы оставить комментарий
N-е число Фибоначчи за O(log N)