Читая статью об устройстве на работу в ABBYY, встретил в ней упоминание задачи:
Для удобства я перейду от обозначения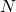 к
к 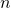 . Также я буду использовать обозначения множеств:
. Также я буду использовать обозначения множеств: 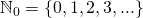 — целые неотрицательные числа,
— целые неотрицательные числа, 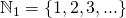 — целые положительные числа. Дело в том, что в разных математических традициях множество натуральных чисел может включать или не включать 0. Поэтому сейчас в международных математических текстах предпочитают указывать это явно.
— целые положительные числа. Дело в том, что в разных математических традициях множество натуральных чисел может включать или не включать 0. Поэтому сейчас в международных математических текстах предпочитают указывать это явно.
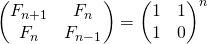
Тождество приводится без доказательства, но довольно просто доказывается по индукции.
Матрица справа иногда называется Q-матрицей.
Обозначим:
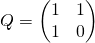
Из тождества получаем, что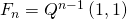 . Т.е. для вычисления
. Т.е. для вычисления 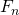 нам нужно вычислить матрицу
нам нужно вычислить матрицу 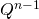 и взять первый элемент первой строки (нумерация с 1).
и взять первый элемент первой строки (нумерация с 1).
Так как вычисление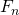 свелось к возведению матрицы в степень, то рассмотрим этот процесс подробнее.
свелось к возведению матрицы в степень, то рассмотрим этот процесс подробнее.
Пусть у нас имеется некоторая матрица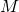 , которую необходимо возвести в степень
, которую необходимо возвести в степень 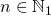 . Предположим также, что
. Предположим также, что 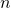 является степенью двойки, т.е.
является степенью двойки, т.е. 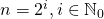 .
.
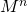 можно представить в виде дерева:
можно представить в виде дерева:
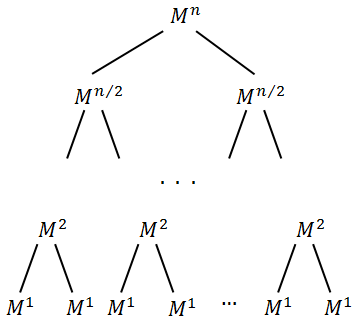
Имеется в виду:
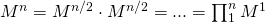 .
.
Соответственно, для вычисления матрицы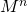 нужно вычислить матрицу
нужно вычислить матрицу 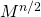 и умножить саму на себя. Для вычисления
и умножить саму на себя. Для вычисления 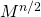 нужно тоже самое проделать с
нужно тоже самое проделать с 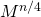 и т.д.
и т.д.
Очевидно, что высота дерева равна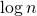 .
.
Оценим время вычисления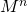 . Матрица
. Матрица 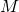 в любой степени имеет постоянный размер. Поэтому умножение двух матриц в любой степени можно выполнить за
в любой степени имеет постоянный размер. Поэтому умножение двух матриц в любой степени можно выполнить за 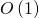 . Всего таких умножений нужно выполнить
. Всего таких умножений нужно выполнить 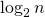 . Следовательно, сложность вычисления
. Следовательно, сложность вычисления 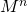 равна
равна 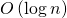 .
.
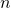 не является степенью двойки? Любое натуральное число
не является степенью двойки? Любое натуральное число 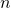 можно разложить как сумму чисел, являющихся степенью двойки, причем без повторений (мы занимаемся этим каждый раз, когда переводим число из двоичной системы счисления в десятичную). Т.е.
можно разложить как сумму чисел, являющихся степенью двойки, причем без повторений (мы занимаемся этим каждый раз, когда переводим число из двоичной системы счисления в десятичную). Т.е.
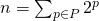 ,
,
где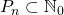 — множество степеней, через которые выражается конкретное
— множество степеней, через которые выражается конкретное 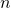 . Если вспомнить, что
. Если вспомнить, что 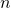 — это степень матрицы, то мы получим:
— это степень матрицы, то мы получим:
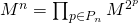 .
.
Хотя в общем произведение матриц не коммутативно, т.е. порядок операндов при умножении важен, но для т.н. перестановочных матриц коммутативность соблюдается. Матрица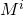 является перестановочной для
является перестановочной для 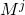 ,
, 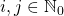 . Следовательно, нам не придется иметь в виду порядок операндов при умножении, что несколько облегчает дело.
. Следовательно, нам не придется иметь в виду порядок операндов при умножении, что несколько облегчает дело.
Итак, алгоритм вычисления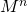 можно представить в виде следующих шагов:
можно представить в виде следующих шагов:
Оценим время работы данного алгоритма.
Первый шаг выполняется за время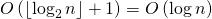 , где
, где 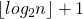 — количество двоичных разрядов в
— количество двоичных разрядов в 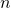 .
.
Второй шаг выполняется за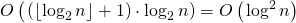 , т.к. нам нужно выполнить не более
, т.к. нам нужно выполнить не более 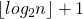 возведение матрицы в степень.
возведение матрицы в степень.
Третий шаг выполняется за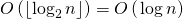 , т.к. нам нужно выполнить умножение матриц не более
, т.к. нам нужно выполнить умножение матриц не более 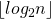 раз.
раз.
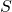 . Нам известно о них то, что для каждой из них
. Нам известно о них то, что для каждой из них 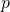 является степенью двойки. Если вернуться к рисунку с деревом, это означает, что они все лежат на тех или иных ярусах дерева и для вычисления больших необходимо вычисление меньших. Если мы применим методику мемоизации и будем сохранять вычисленные матрицы на всех ярусах дерева, то сможем сократить время работы второго шага до
является степенью двойки. Если вернуться к рисунку с деревом, это означает, что они все лежат на тех или иных ярусах дерева и для вычисления больших необходимо вычисление меньших. Если мы применим методику мемоизации и будем сохранять вычисленные матрицы на всех ярусах дерева, то сможем сократить время работы второго шага до 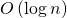 и время выполнения всего алгоритма также до
и время выполнения всего алгоритма также до 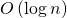 . Именно это и требуется нам по условию задачи.
. Именно это и требуется нам по условию задачи.
Получается такое:
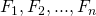 с сохранением предыдущих двух чисел. Я реализовал его так:
с сохранением предыдущих двух чисел. Я реализовал его так:
Применялась следующая методика тестирования производительности. Число принимает значения
принимает значения 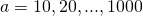 . Для каждого
. Для каждого  создаются объекты классов
создаются объекты классов 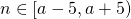 . Каждый из объектов вычисляет
. Каждый из объектов вычисляет 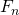 с замером времени. На выходе теста получается множество строк вида:
с замером времени. На выходе теста получается множество строк вида:
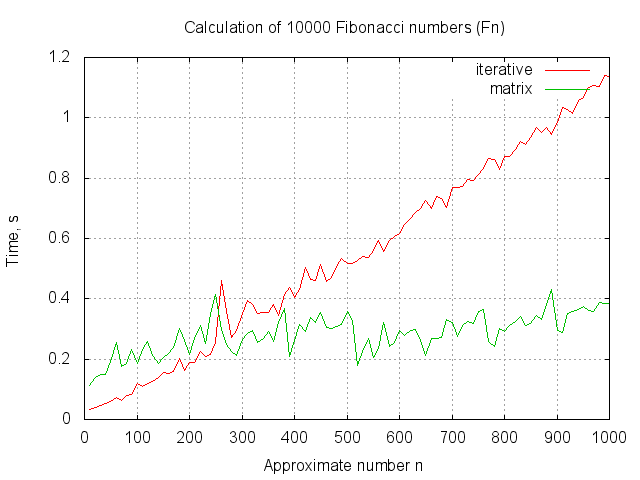
Как видно из графика, матричный алгоритм начинает уверенно обгонять итерационный начиная где-то с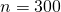 (cтоит заметить, что
(cтоит заметить, что 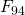 уже не влезет в 64 бита без знака). Мне кажется, что можно говорить о непрактичности данного алгоритма, хотя и имеющего хорошую теоретическую скорость.
уже не влезет в 64 бита без знака). Мне кажется, что можно говорить о непрактичности данного алгоритма, хотя и имеющего хорошую теоретическую скорость.
Полный код с бенчмарком выложен тут. Код для gnuplot для построения графика по данным — тут.
P.S. Хотел попросить прощения за то, что TeX-формулы в виде картинок не всегда адекватно выравниваются внутри строчки. И похоже, что на Хабре нельзя сделать выравнивание руками.
быстро – за O( log N ) арифметических операций над числами – найти N-е число ФибоначчиЯ задумался над ней и понял, что сходу в голову приходят только решения, работающие за время O(N). Однако позже решение было найдено.
Для удобства я перейду от обозначения
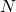 к
к 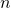 . Также я буду использовать обозначения множеств:
. Также я буду использовать обозначения множеств: 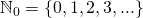 — целые неотрицательные числа,
— целые неотрицательные числа, 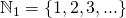 — целые положительные числа. Дело в том, что в разных математических традициях множество натуральных чисел может включать или не включать 0. Поэтому сейчас в международных математических текстах предпочитают указывать это явно.
— целые положительные числа. Дело в том, что в разных математических традициях множество натуральных чисел может включать или не включать 0. Поэтому сейчас в международных математических текстах предпочитают указывать это явно.Итак, решение
Кнут [1, с. 112] приводит матричное тождество следующего вида: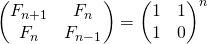
Тождество приводится без доказательства, но довольно просто доказывается по индукции.
Матрица справа иногда называется Q-матрицей.
Обозначим:
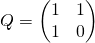
Из тождества получаем, что
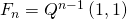 . Т.е. для вычисления
. Т.е. для вычисления 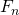 нам нужно вычислить матрицу
нам нужно вычислить матрицу 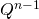 и взять первый элемент первой строки (нумерация с 1).
и взять первый элемент первой строки (нумерация с 1).Так как вычисление
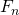 свелось к возведению матрицы в степень, то рассмотрим этот процесс подробнее.
свелось к возведению матрицы в степень, то рассмотрим этот процесс подробнее.Пусть у нас имеется некоторая матрица
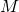 , которую необходимо возвести в степень
, которую необходимо возвести в степень 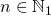 . Предположим также, что
. Предположим также, что 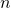 является степенью двойки, т.е.
является степенью двойки, т.е. 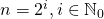 .
.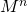 можно представить в виде дерева:
можно представить в виде дерева:
Имеется в виду:
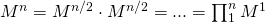 .
.Соответственно, для вычисления матрицы
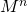 нужно вычислить матрицу
нужно вычислить матрицу 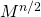 и умножить саму на себя. Для вычисления
и умножить саму на себя. Для вычисления 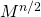 нужно тоже самое проделать с
нужно тоже самое проделать с 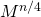 и т.д.
и т.д.Очевидно, что высота дерева равна
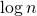 .
.Оценим время вычисления
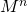 . Матрица
. Матрица 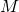 в любой степени имеет постоянный размер. Поэтому умножение двух матриц в любой степени можно выполнить за
в любой степени имеет постоянный размер. Поэтому умножение двух матриц в любой степени можно выполнить за 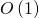 . Всего таких умножений нужно выполнить
. Всего таких умножений нужно выполнить 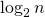 . Следовательно, сложность вычисления
. Следовательно, сложность вычисления 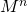 равна
равна 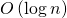 .
.А если n — не степень двойки?
Теперь же встает вопрос: что делать, если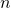 не является степенью двойки? Любое натуральное число
не является степенью двойки? Любое натуральное число 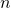 можно разложить как сумму чисел, являющихся степенью двойки, причем без повторений (мы занимаемся этим каждый раз, когда переводим число из двоичной системы счисления в десятичную). Т.е.
можно разложить как сумму чисел, являющихся степенью двойки, причем без повторений (мы занимаемся этим каждый раз, когда переводим число из двоичной системы счисления в десятичную). Т.е. 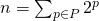 ,
,где
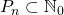 — множество степеней, через которые выражается конкретное
— множество степеней, через которые выражается конкретное 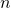 . Если вспомнить, что
. Если вспомнить, что 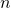 — это степень матрицы, то мы получим:
— это степень матрицы, то мы получим: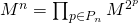 .
.Хотя в общем произведение матриц не коммутативно, т.е. порядок операндов при умножении важен, но для т.н. перестановочных матриц коммутативность соблюдается. Матрица
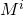 является перестановочной для
является перестановочной для 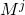 ,
, 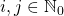 . Следовательно, нам не придется иметь в виду порядок операндов при умножении, что несколько облегчает дело.
. Следовательно, нам не придется иметь в виду порядок операндов при умножении, что несколько облегчает дело.Итак, алгоритм вычисления
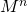 можно представить в виде следующих шагов:
можно представить в виде следующих шагов:- Разложить
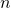 на сумму степеней двойки в виде множества
на сумму степеней двойки в виде множества 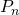 .
. - Вычислить все элементы множества
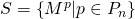 .
. - Вычислить
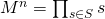 .
.
Оценим время работы данного алгоритма.
Первый шаг выполняется за время
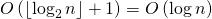 , где
, где 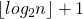 — количество двоичных разрядов в
— количество двоичных разрядов в 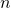 .
.Второй шаг выполняется за
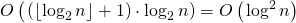 , т.к. нам нужно выполнить не более
, т.к. нам нужно выполнить не более 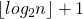 возведение матрицы в степень.
возведение матрицы в степень.Третий шаг выполняется за
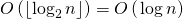 , т.к. нам нужно выполнить умножение матриц не более
, т.к. нам нужно выполнить умножение матриц не более 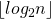 раз.
раз.Оптимизация
Можно ли улучшить время работы данного алгоритма? Да, можно. Заметим, что во втором шаге в общем-то не оговаривается метод вычисления матриц, входящих во множество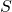 . Нам известно о них то, что для каждой из них
. Нам известно о них то, что для каждой из них 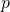 является степенью двойки. Если вернуться к рисунку с деревом, это означает, что они все лежат на тех или иных ярусах дерева и для вычисления больших необходимо вычисление меньших. Если мы применим методику мемоизации и будем сохранять вычисленные матрицы на всех ярусах дерева, то сможем сократить время работы второго шага до
является степенью двойки. Если вернуться к рисунку с деревом, это означает, что они все лежат на тех или иных ярусах дерева и для вычисления больших необходимо вычисление меньших. Если мы применим методику мемоизации и будем сохранять вычисленные матрицы на всех ярусах дерева, то сможем сократить время работы второго шага до 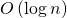 и время выполнения всего алгоритма также до
и время выполнения всего алгоритма также до 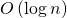 . Именно это и требуется нам по условию задачи.
. Именно это и требуется нам по условию задачи.Код
Перейдем к кодированию. Я реализовал алгоритм на Python по двум причинам:- он достаточно выразителен, чтобы заменить псевдокод;
- в нем прозрачная длинная арифметика.
Получается такое:
class MatrixFibonacci:
Q = [[1, 1],
[1, 0]]
def __init__(self):
self.__memo = {}
def __multiply_matrices(self, M1, M2):
"""Умножение матриц
(ожидаются матрицы в виде списка список размером 2x2)."""
a11 = M1[0][0]*M2[0][0] + M1[0][1]*M2[1][0]
a12 = M1[0][0]*M2[0][1] + M1[0][1]*M2[1][1]
a21 = M1[1][0]*M2[0][0] + M1[1][1]*M2[1][0]
a22 = M1[1][0]*M2[0][1] + M1[1][1]*M2[1][1]
r = [[a11, a12], [a21, a22]]
return r
def __get_matrix_power(self, M, p):
"""Возведение матрицы в степень (ожидается p равная степени двойки)."""
if p == 1:
return M
if p in self.__memo:
return self.__memo[p]
K = self.__get_matrix_power(M, int(p/2))
R = self.__multiply_matrices(K, K)
self.__memo[p] = R
return R
def get_number(self, n):
"""Получение n-го числа Фибоначчи
(в качестве n ожидается неотрицательное целое число)."""
if n == 0:
return 0
if n == 1:
return 1
# Разложение переданной степени на степени, равные степени двойки,
# т.е. 62 = 2^5 + 2^4 + 2^3 + 2^2 + 2^0 = 32 + 16 + 8 + 4 + 1.
powers = [int(pow(2, b))
for (b, d) in enumerate(reversed(bin(n-1)[2:])) if d == '1']
# Тоже самое, но менее pythonic: http://pastebin.com/h8cKDkHX
matrices = [self.__get_matrix_power(MatrixFibonacci.Q, p)
for p in powers]
while len(matrices) > 1:
M1 = matrices.pop()
M2 = matrices.pop()
R = self.__multiply_matrices(M1, M2)
matrices.append(R)
return matrices[0][0][0]
mfib = MatrixFibonacci()
for n in range(0, 128):
num = mfib.get_number(n)
print(num)
Бенчмарк
Я хотел сравнить производительность моего алгоритма с классическим итерационным алгоритмом, основанным на последовательном вычислении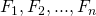 с сохранением предыдущих двух чисел. Я реализовал его так:
с сохранением предыдущих двух чисел. Я реализовал его так:Реализация
def get_number(self, n):
if n == 0:
return 0
a = 0
b = 1
c = 1
for i in range(n-1):
c = a + b
a = b
b = c
return c
Применялась следующая методика тестирования производительности. Число
 принимает значения
принимает значения 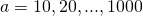 . Для каждого
. Для каждого  создаются объекты классов
создаются объекты классов MatrixFibonacci и IterationFibonacci (класс, вычисляющий числа Фибоначчи итерационно). Далее 10 000 раз генерируется случайное целое 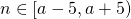 . Каждый из объектов вычисляет
. Каждый из объектов вычисляет 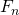 с замером времени. На выходе теста получается множество строк вида:
с замером времени. На выходе теста получается множество строк вида: n <tab> T1 <tab> T2. По данным строкам строится график.
Как видно из графика, матричный алгоритм начинает уверенно обгонять итерационный начиная где-то с
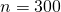 (cтоит заметить, что
(cтоит заметить, что 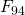 уже не влезет в 64 бита без знака). Мне кажется, что можно говорить о непрактичности данного алгоритма, хотя и имеющего хорошую теоретическую скорость.
уже не влезет в 64 бита без знака). Мне кажется, что можно говорить о непрактичности данного алгоритма, хотя и имеющего хорошую теоретическую скорость.Полный код с бенчмарком выложен тут. Код для gnuplot для построения графика по данным — тут.
P.S. Хотел попросить прощения за то, что TeX-формулы в виде картинок не всегда адекватно выравниваются внутри строчки. И похоже, что на Хабре нельзя сделать выравнивание руками.