Итак, тема рейтинговых систем продолжает будоражить умы хабрапользователей. Появляются всё новые и новые схемы, формулы, тесты. И каждый раз всё сводится к одному и тому же вопросу: как совместить среднюю оценку пользователей с нашей уверенностью в этой оценке. Например, если один фильм получил 80 положительных и 20 отрицательных голосов, а другой — 9 положительных и 1 отрицательный, то какой из фильмов лучше? Не претендуя на создание новой универсальной рейтинговой системы, я всё же предложу один из возможных подходов к решению именно этого вопроса.
Вообще, сама формулировка — оценить некоторое значение и нашу уверенность в нём — наталкивает на мысль об использовании модели распределения вероятностей, например, нормального распределения.
Рейтинг, как правило, это просто число, какой-то конечный результат оценивания. А собственно оценивать мы будем предполагаемое качество фильма (кофемолки, статьи, пользователя — нужно подчеркнуть). На графике ниже показаны графики распределений для двух гипотетических фильмов.
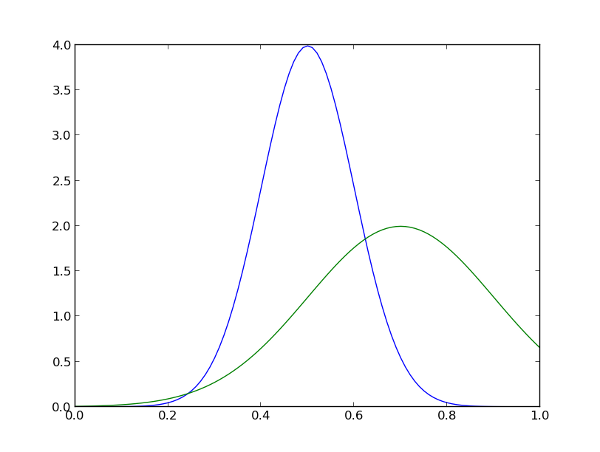
Первый фильм (синяя линия) вызвал противоречивые отзывы (среднее значение распределения равно 0.5). В отличие от него, второй фильм (зелёная линия) получил больше положительных, чем отрицательных оценок, однако людей проголосовало гораздо меньше, поэтому и в результате мы уверены гораздо меньше (дисперсия гораздо больше, чем в первом графике).
В принципе, нормальное распределение само по себе уже позволяет неплохо моделировать рейтинг (теоретическое об��снование для этого даёт центральная предельная теорема). Однако в статистике есть и более удобный инструмент для этого.
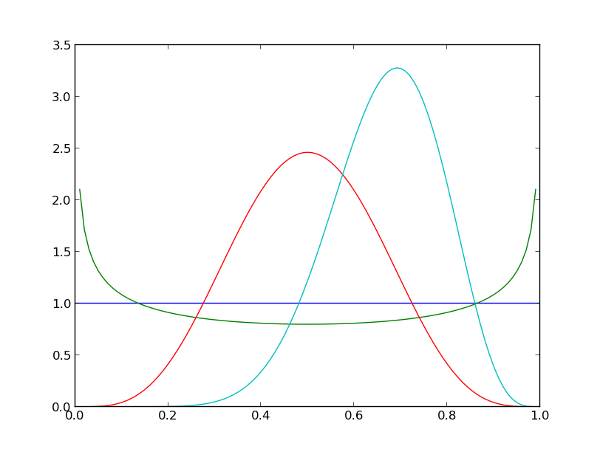
Так же, как и нормальное, бета-распределение задаётся двумя параметрами — alpha > 0 и beta > 0 (записывается как X ~ B(alpha, beta)). Одако в отличие от нормального, всегда имеющего форму колокола, бета-распределение обладает гораздо большей гибкостью. В частности, при alpha = 1 и beta = 1 данное распределение превращается в равномерное (тёмно-синяя линия на рисунке внизу), при alpha < 1 и beta < 1 функция распределения принимает форму колодца (зелёная линия), а при alpha > 1 и beta > 1 становится похожа на нормальное (красная и светло-голубая линии).
Кроме этого, бета-распределение обладает несколькими интересными свойствами:
А что, если использовать в качестве параметров alpha и beta соответственно количество положительных и количество отрицательных оценок пользователей? При этом изначально бета распределение можно инициализировать единицами для обоих параметров (что, вообще говоря, будет соответствовать лапласовскому сглаживанию). В этом случае изначально наша оценка относительно качества фильма будет равномерно распределена (мы ничего не знаем о нём), а каждый голос будет увеличивать один из параметров, уменьшать дисперсию и сдвигать график либо вправо (alpha параметр, положительные отзывы), либо влево (beta параметр, отрицательные отзывы). При этом наша оценка качества фильма никогда не выйдет за пределы интервала [0..1] и, по сути, будет показывать вероятность того, что фильм понравится среднестатистическому зрителю.
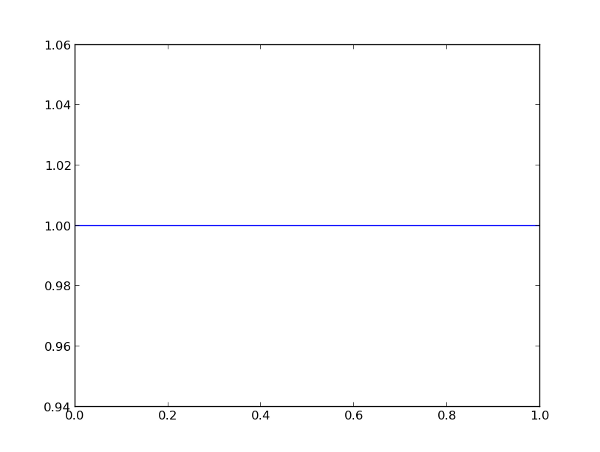
Рассмотрим несколько примеров. Когда появляется новый фильм, про который ещё никто не высказал своё мнение, его параметры alpha и beta будут равны единице, а график плотности будет эквивалентен графику равномерного распределения:
Оказалось, что информацию о фильме загрузил сам режисёр. Сам загрузил, и сам же проголосовал. Естественно, положительно. Да ещё и пятерых своих помощников попросил помочь. Итог: alpha = 1 + 1 + 5 = 7, beta = 1.
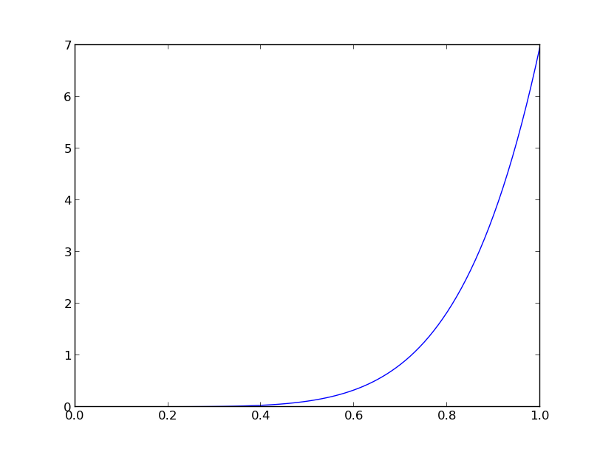
Бывшая жена режиссёра увидела страницу фильма и решила подпортить рейтинг, вместе с любовником проголосовав отрицательно. Итог: alpha = 7, beta = 1 + 2 = 3:
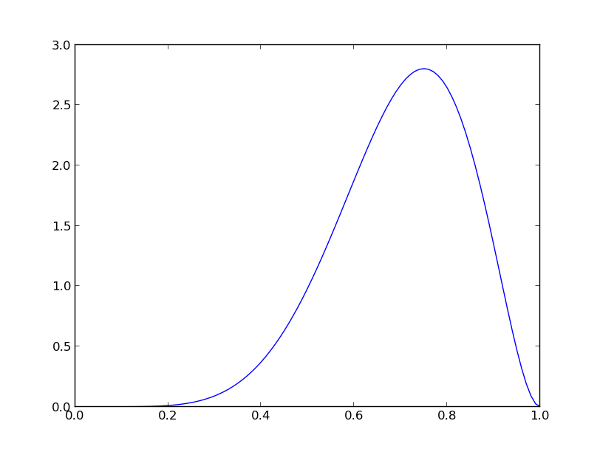
После 8 голосов средняя оценка, с учётом лапласовского сглаживания, будет равна alpha / (alpha + beta) = 7 / 10 = 0.7. Однако из графика видно, что дисперсия получившегося распределения всё ещё высока, а значит наша уверенность в такой оценке — низкая.
Предположим, что в течении первой недели проката за фильм проголосовало ещё 90 человек, причём так, что параметр alpha в итоге оказался равен 70, а beta — 30. Средняя оценка будет, как и раньше, равна 70 / 100 = 0.7, однако график значительно изменится:

Дисперсия на втором графике гораздо меньше. Т.е. при увеличении количества голосов наша уверененность в оценке качества фильма также увеличивается.
Всё это хорошо, но пользователь не хочет видеть какие-то странные графики. Ему нужен рейтинг — цифра, по которой он сможет определить, стоит ли смотреть фильмили лучше пойти почитать книгу. В принципе, имея параметры бета-распределения можно посчитать среднюю оценку и дисперсию, и каким-то образом пытаться их комбинировать (например, делить среднюю оценку на логарифм дисперсии). Но можно пойти и более статистически правильным путём.
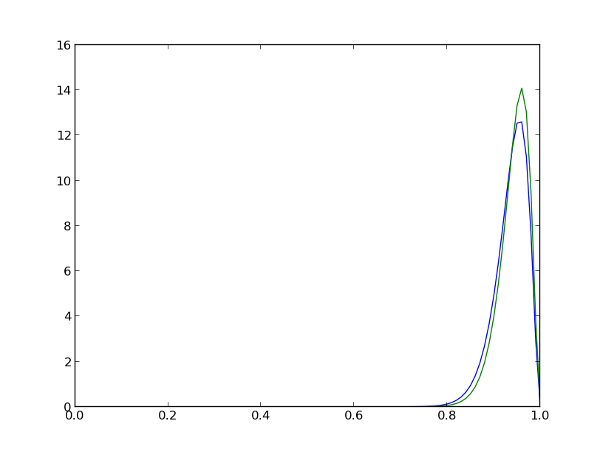
Чтобы разговор был более предметным, возьмём для примера 2 фильма: один из предыдущего раздела с распределением B(70, 30) и другой, более популярный, с распределением B(650, 350). Графики распределений изображены на рисунке ниже:
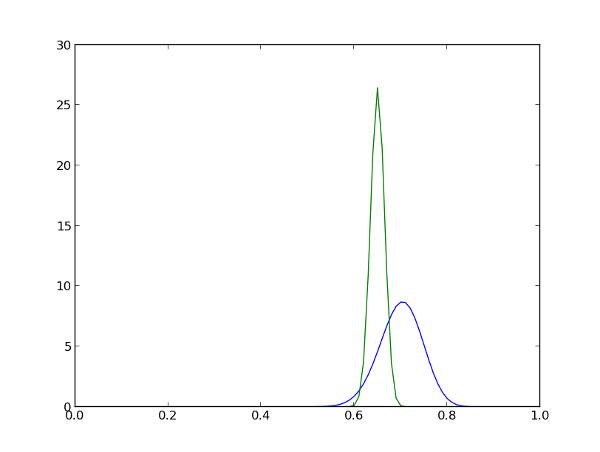
С одной стороны, среднее значение оценок для первого фильма выше — 0.7 против 0.65. Однако, второй фильм посмотрело гораздо больше людей, поэтому ещё неизвестно, какова была бы оценка первого фильма после такого же количества отзывов. Так как же их сравнить?
Один из вариантов сравнения — это посчитать минимальное доверительное качество фильма, число, показывающее минимальную оценку, которую может получить фильм после бесконечного количества отзывов. В статистике не принято доводить всё до абсолюта, поэтому в качестве уровня доверия возьмём не 100%, а стандартные 95%. Это означает, что мы хотим быть на 95% уверены, что фильм не хуже, чем X. Графически это означает, что 95% площади под графиком должно находиться справа от X:
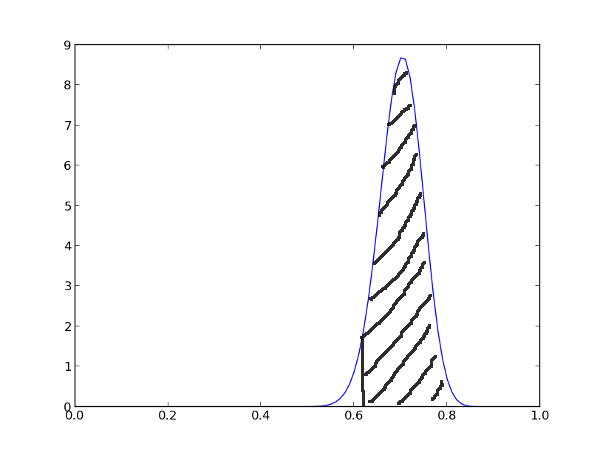
После подсчётов получилось, что с 95% вероятностью первый фильм в конечном итоге понравится как минимум 0.6227 от всех зрителей, а вот второй — 0.6250 из них. Разница всего в две тысячные, но если использовать эти оценки в рейтинге, то второй фильм, даже при меньшей средней оценке, окажется выше в списке.
Те же расчёты можно повторить и для фильмов, указанных в самом начале поста: для фильма с пропорцией 80/20 минимальное доверительное качество будет равно 0.731, а для фильма с пропорцией 9/1 — 0.717, т.е. количество голосов снова перевешивает среднюю оценку. Однако стоит добавить второму фильму всего один голос «за», и наш коэффициент для него становится равен 0.741, выводя его на первое место.
Все коэффициенты, указанные здесь, взяты, по большому счёту, на глаз. Хотя, кажется, они и дают довольно вменяемый результат, в реальном приложении есть смысл попробовать для них разные значения. Например, при большом количестве пользователей, голосующих за фильмы, имеет смысл увеличивать параметры не на 1, а, например, на 0.5 для каждого голоса. Или даже вводить коэффициент затухания, когда каждый следующий голос имеет меньший вес, чем предыдущий — таким образом можно добиться замедления роста коэффициентов.
Кроме того, можно улучшить и изначальную оценку относительно фильма. В данной статье я исходил из того, что изначально мы ничего не знаем ни о самом фильме, ни о других фильмах у нас в системе, поэтому в начале фильму присваивается равномерное распределение (alpha = 1, beta = 1). Однако на практике мы, как правило, что-то уже знаем о фильме заранее и можем использовать эту информацию в качестве априорной оценки. Например, мы можем посчитать среднюю оценку для предыдущих фильмов этого режиссёра и инициализировать параметры бета-распределения соответствующим образом. Даже если мы ничего не знаем о режиссёре (продюсе, сценаристе, актёрском составе), мы можем использовать среднюю оценку по всем фильмам в нашей базе данных.
В принципе, метод можно расширить и для более градированных оценок, например, для шкалы от 0 до 10. В этом случае оценки выше 5 будут прибавляться к параметру alpha, ниже 5 — к beta, а при оценке ровно 5 — и alpha, и beta увеличиваются на 0.5 (привет Хабр!).
Наконец, можно варьировать требуемую степень уверенности в ответе или даже менять подход, используя вместо минимального доверительного качества площадь под графиком внутри некоторого фиксированного интервала.
Аппроксимация нормальным распределением
Вообще, сама формулировка — оценить некоторое значение и нашу уверенность в нём — наталкивает на мысль об использовании модели распределения вероятностей, например, нормального распределения.
Что такое нормальное распределени?!
Для тех, кто прогуливал пары мат. статистики, напомню, что из себя представляет нормальное распределение, да и вообще распределение вероятностей. Допустим, мы пришли на остановку и увидели, как прямо перед нами уехал автобус. Мы знаем, что следующий приедет примерно через 15 минут (на 15й минуте). Ну, может на 16й. Или наоборот, на 14й. В принципе, водитель может поторопиться и приехать уже на 12 минуте, но вероятность этого гораздо ниже. График внизу как раз и показывает распределение вероятностей приезда автобуса в каждую минуту: скорее всего он приедет на 15й минуте, с чуть-чуть меньшей вероятностью — на 14й или 16й, и совсем с небольшой вероятностью на 12й или 18й.
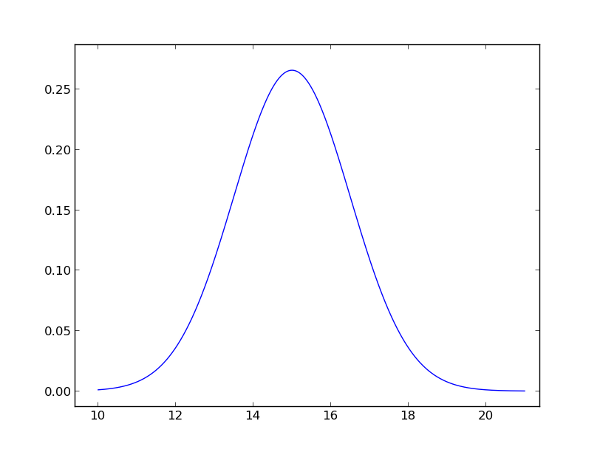
При этом следует понимать, что значение по оси Y — это не вероятность, а плотность вероятности (probability density function, PDF). Сама вероятность высчитывается как площадь под графиком между двумя значениями X1 и X2, например, вероятность, что автобус придёт между 15 и 16 минутой в данном случае равна 0.248. Но об этом позже.
Нормальное распределение характеризуется двумя параметрами — средним значеним (mean, здесь — 15 минут) и дисперсией (variance, разброс), которая показывает степень неопределённости среднего значения: чем больше дисперсия, тем шире график, и тем меньше мы уверены в том, когда же наконец придёт этот автобус.

При этом следует понимать, что значение по оси Y — это не вероятность, а плотность вероятности (probability density function, PDF). Сама вероятность высчитывается как площадь под графиком между двумя значениями X1 и X2, например, вероятность, что автобус придёт между 15 и 16 минутой в данном случае равна 0.248. Но об этом позже.
Нормальное распределение характеризуется двумя параметрами — средним значеним (mean, здесь — 15 минут) и дисперсией (variance, разброс), которая показывает степень неопределённости среднего значения: чем больше дисперсия, тем шире график, и тем меньше мы уверены в том, когда же наконец придёт этот автобус.
Рейтинг, как правило, это просто число, какой-то конечный результат оценивания. А собственно оценивать мы будем предполагаемое качество фильма (кофемолки, статьи, пользователя — нужно подчеркнуть). На графике ниже показаны графики распределений для двух гипотетических фильмов.

Первый фильм (синяя линия) вызвал противоречивые отзывы (среднее значение распределения равно 0.5). В отличие от него, второй фильм (зелёная линия) получил больше положительных, чем отрицательных оценок, однако людей проголосовало гораздо меньше, поэтому и в результате мы уверены гораздо меньше (дисперсия гораздо больше, чем в первом графике).
В принципе, нормальное распределение само по себе уже позволяет неплохо моделировать рейтинг (теоретическое об��снование для этого даёт центральная предельная теорема). Однако в статистике есть и более удобный инструмент для этого.
Бета-распределение
Так же, как и нормальное, бета-распределение задаётся двумя параметрами — alpha > 0 и beta > 0 (записывается как X ~ B(alpha, beta)). Одако в отличие от нормального, всегда имеющего форму колокола, бета-распределение обладает гораздо большей гибкостью. В частности, при alpha = 1 и beta = 1 данное распределение превращается в равномерное (тёмно-синяя линия на рисунке внизу), при alpha < 1 и beta < 1 функция распределения принимает форму колодца (зелёная линия), а при alpha > 1 и beta > 1 становится похожа на нормальное (красная и светло-голубая линии).

programming exercise
Было бы нечестно и дальше продолжать показывать графики и не рассказывать, как их нарисовать и поиграться с параметрами, поэтому здесь и ниже я буду показывать примеры кода для генерации каждого изображения. Примеры будут на Python с использованием библиотек NumPy, SciPy и matplotlib (все три доступны из pip), однако их можно элементарно перенести на R, Matlab/Octave, Java и даже JavaScript.
Для всех примеров понадобатся следующие импорты:
Предыдущий график был сгенерирован следующим кодом:
Для всех примеров понадобатся следующие импорты:
from numpy import *
import scipy.stats as ss
import pylab as plt
Предыдущий график был сгенерирован следующим кодом:
x = arange(101) / 100.
plt.plot(x, ss.beta(1, 1).pdf(x))
plt.plot(x, ss.beta(.7, .7).pdf(x))
plt.plot(x, ss.beta(5, 5).pdf(x))
plt.plot(x, ss.beta(10, 5).pdf(x))
plt.show()
Кроме этого, бета-распределение обладает несколькими интересными свойствами:
- Оно ограничено конечным интервалом. Если мы хотим «запереть» возможные значения в интервал от 0 до 1, то бета-распределение — как раз то, что надо.
- Оно симметрично относительно своих параметров. График B(alpha, beta) будет зеркальным отражением графика B(beta, alpha).
- alpha и beta действуют на разные стороны графика плотности. При увеличении alpha график смещается и наклоняется вправо, при увеличении beta — наоборот, влево.
- Дисперсия при увеличении любого из параметров уменьшается.
Оценки пользователей
А что, если использовать в качестве параметров alpha и beta соответственно количество положительных и количество отрицательных оценок пользователей? При этом изначально бета распределение можно инициализировать единицами для обоих параметров (что, вообще говоря, будет соответствовать лапласовскому сглаживанию). В этом случае изначально наша оценка относительно качества фильма будет равномерно распределена (мы ничего не знаем о нём), а каждый голос будет увеличивать один из параметров, уменьшать дисперсию и сдвигать график либо вправо (alpha параметр, положительные отзывы), либо влево (beta параметр, отрицательные отзывы). При этом наша оценка качества фильма никогда не выйдет за пределы интервала [0..1] и, по сути, будет показывать вероятность того, что фильм понравится среднестатистическому зрителю.
Рассмотрим несколько примеров. Когда появляется новый фильм, про который ещё никто не высказал своё мнение, его параметры alpha и beta будут равны единице, а график плотности будет эквивалентен графику равномерного распределения:

programming exercise
# продолжая предыдущий пример
plt.plot(x, ss.beta(1, 1).pdf(x))
plt.show()
Оказалось, что информацию о фильме загрузил сам режисёр. Сам загрузил, и сам же проголосовал. Естественно, положительно. Да ещё и пятерых своих помощников попросил помочь. Итог: alpha = 1 + 1 + 5 = 7, beta = 1.

programming exercise
# всё аналогично
plt.plot(x, ss.beta(7, 1).pdf(x))
plt.show()
Бывшая жена режиссёра увидела страницу фильма и решила подпортить рейтинг, вместе с любовником проголосовав отрицательно. Итог: alpha = 7, beta = 1 + 2 = 3:

programming exercise
plt.plot(x, ss.beta(7, 3).pdf(x))
plt.show()
После 8 голосов средняя оценка, с учётом лапласовского сглаживания, будет равна alpha / (alpha + beta) = 7 / 10 = 0.7. Однако из графика видно, что дисперсия получившегося распределения всё ещё высока, а значит наша уверенность в такой оценке — низкая.
Предположим, что в течении первой недели проката за фильм проголосовало ещё 90 человек, причём так, что параметр alpha в итоге оказался равен 70, а beta — 30. Средняя оценка будет, как и раньше, равна 70 / 100 = 0.7, однако график значительно изменится:

programming exercise
plt.plot(x, ss.beta(70, 30).pdf(x))
plt.show()
Дисперсия на втором графике гораздо меньше. Т.е. при увеличении количества голосов наша уверененность в оценке качества фильма также увеличивается.
Рейтинг
Всё это хорошо, но пользователь не хочет видеть какие-то странные графики. Ему нужен рейтинг — цифра, по которой он сможет определить, стоит ли смотреть фильм
Чтобы разговор был более предметным, возьмём для примера 2 фильма: один из предыдущего раздела с распределением B(70, 30) и другой, более популярный, с распределением B(650, 350). Графики распределений изображены на рисунке ниже:

programming exercise
plt.plot(x, ss.beta(70, 30).pdf(x))
plt.plot(x, ss.beta(650, 350).pdf(x))
plt.show()
С одной стороны, среднее значение оценок для первого фильма выше — 0.7 против 0.65. Однако, второй фильм посмотрело гораздо больше людей, поэтому ещё неизвестно, какова была бы оценка первого фильма после такого же количества отзывов. Так как же их сравнить?
Один из вариантов сравнения — это посчитать минимальное доверительное качество фильма, число, показывающее минимальную оценку, которую может получить фильм после бесконечного количества отзывов. В статистике не принято доводить всё до абсолюта, поэтому в качестве уровня доверия возьмём не 100%, а стандартные 95%. Это означает, что мы хотим быть на 95% уверены, что фильм не хуже, чем X. Графически это означает, что 95% площади под графиком должно находиться справа от X:

programming exercise
Практически все статистические библиотеки для всех реализованных распределений предоставляют функцию вероятности (cumulative probability function, CDF), которая принимает на вход значение и возвращает вероятность, что случайная величина окажется меньше этого значения. Т.е. по сути функция CDF от некоторого значения X возвращает площадь под графиком между нулём и X. Это отличается от того, что нам нужно, в двух аспектах.
Во-первых, нам нужна площадь с другой стороны — от X до 1. К счастью, как уже говорилось выше, бета-функция является симметричной относительно своих параметров, поэтому вместо прямого бета-распределения B(alpha, beta) мы можем работать с обратным — B(beta, alpha).
Во-вторых, нам нужна функция, которая по заданной степени уверенности (проценту от всей площади графика) вернёт искомое значение X. Чаще всего в мат. пакетах эта функция называется inverse CDF или как-то так, но в SciPy используется название PPF (percent point function, в литературе также встречается под названием quantile funtion).
Итого, чтобы получить значение минимального доверительного качества фильма можно использовать следующий код:
Во-первых, нам нужна площадь с другой стороны — от X до 1. К счастью, как уже говорилось выше, бета-функция является симметричной относительно своих параметров, поэтому вместо прямого бета-распределения B(alpha, beta) мы можем работать с обратным — B(beta, alpha).
Во-вторых, нам нужна функция, которая по заданной степени уверенности (проценту от всей площади графика) вернёт искомое значение X. Чаще всего в мат. пакетах эта функция называется inverse CDF или как-то так, но в SciPy используется название PPF (percent point function, в литературе также встречается под названием quantile funtion).
Итого, чтобы получить значение минимального доверительного качества фильма можно использовать следующий код:
dist1 = ss.beta(70, 30) # распределение для первого фильма, просто для справки
dist2 = ss.beta(650, 350) # распределение для второго фильма, тоже просто для справки
idist1 = ss.beta(30, 70) # распределение, обратное первому
idist2 = ss.beta(350, 650) # распределение, обратное второму
q1 = 1 - idist1.ppf(.95) # минимальное качество первого фильма с уровнем уверенности 95%
q2 = 1 - idist2.ppf(.95) # минимальное качество второго фильма с уровнем уверенности 95%
...
>>> q1
0.62272854953840073
>>> q2
0.62503161244929017
После подсчётов получилось, что с 95% вероятностью первый фильм в конечном итоге понравится как минимум 0.6227 от всех зрителей, а вот второй — 0.6250 из них. Разница всего в две тысячные, но если использовать эти оценки в рейтинге, то второй фильм, даже при меньшей средней оценке, окажется выше в списке.
Те же расчёты можно повторить и для фильмов, указанных в самом начале поста: для фильма с пропорцией 80/20 минимальное доверительное качество будет равно 0.731, а для фильма с пропорцией 9/1 — 0.717, т.е. количество голосов снова перевешивает среднюю оценку. Однако стоит добавить второму фильму всего один голос «за», и наш коэффициент для него становится равен 0.741, выводя его на первое место.
Вариации, достоинства и недостатки
Все коэффициенты, указанные здесь, взяты, по большому счёту, на глаз. Хотя, кажется, они и дают довольно вменяемый результат, в реальном приложении есть смысл попробовать для них разные значения. Например, при большом количестве пользователей, голосующих за фильмы, имеет смысл увеличивать параметры не на 1, а, например, на 0.5 для каждого голоса. Или даже вводить коэффициент затухания, когда каждый следующий голос имеет меньший вес, чем предыдущий — таким образом можно добиться замедления роста коэффициентов.
Кроме того, можно улучшить и изначальную оценку относительно фильма. В данной статье я исходил из того, что изначально мы ничего не знаем ни о самом фильме, ни о других фильмах у нас в системе, поэтому в начале фильму присваивается равномерное распределение (alpha = 1, beta = 1). Однако на практике мы, как правило, что-то уже знаем о фильме заранее и можем использовать эту информацию в качестве априорной оценки. Например, мы можем посчитать среднюю оценку для предыдущих фильмов этого режиссёра и инициализировать параметры бета-распределения соответствующим образом. Даже если мы ничего не знаем о режиссёре (продюсе, сценаристе, актёрском составе), мы можем использовать среднюю оценку по всем фильмам в нашей базе данных.
В принципе, метод можно расширить и для более градированных оценок, например, для шкалы от 0 до 10. В этом случае оценки выше 5 будут прибавляться к параметру alpha, ниже 5 — к beta, а при оценке ровно 5 — и alpha, и beta увеличиваются на 0.5 (привет Хабр!).
Наконец, можно варьировать требуемую степень уверенности в ответе или даже менять подход, используя вместо минимального доверительного качества площадь под графиком внутри некоторого фиксированного интервала.
График Beta-распределения для этой статьи