Смазанные изображения — один из самых неприятных дефектов в фотографии, наравне с расфокусированными изображениями. Ранее я писал про алгоритмы деконволюции для восстановления смазанных и расфокусированных изображений. Эти, относительно простые, подходы позволяют восстановить исходное изображение, если известна точная траектория смаза (или форма пятна размытия).
В большинстве случаев траектория смаза предполагается прямой линией, параметры которой должен задавать сам пользователь — для этого требуется достаточно кропотливая работа по подбору ядра, кроме того, в реальных фотографиях траектория смаза далека от линии и представляет собой замысловатую кривую переменной плотности/яркости, форму которой крайне сложно подобрать вручную.

В последние несколько лет интенсивно развивается новое направлении в теории восстановления изображений — слепая обратная свертка (Blind Deconvolution). Появилось достаточно много работ по этой теме, и начинается активное коммерческое использование результатов.
Многие из вас помнят конференцию Adobe MAX 2011, на которой они как раз показали работу одного из алгоритмов Blind Deconvolution: Исправление смазанных фотографий в новой версии Photoshop
В этой статье я хочу подробнее рассказать — как же работает эта удивительная технология, а также показать практическую реализацию SmartDeblur, который теперь тоже имеет в своем распоряжении этот алгоритм.
Внимание, под катом много картинок!
Часть 1. Теория — Восстановление расфокусированных и смазанных изображений
Часть 2. Практика — Восстановление расфокусированных и смазанных изображений
Часть 3. Повышаем качество — Восстановление расфокусированных и смазанных изображений
Рекомендуется прочитать хотя бы первую теоретическую часть, чтобы лучше понимать, что такое свертка, деконволюция, преобразование Фурье и прочие термины. Хоть я и обещал, что третья часть будет последней, но не смог удержаться и не рассказать про последние веяния в области восстановления изображений.
Я буду рассматривать Blind Decovolution на примере работы американского профессора Rob Fergus «Removing Camera Shake from a Single Photograph». Оригинал статьи можно найти на его страничке: http://cs.nyu.edu/~fergus/pmwiki/pmwiki.php
Это не самая новая работа, в последнее время появилось много других публикаций, которые демонстрируют лучшие результаты — но там используется совсем сложная математика ((для неподготовленного читателя) в ряде этапов, а основной принцип остается тем же. К тому же, работа Фергуса является своего рода «классикой», он одним из первых предложил принципиально новый подход, который позволил автоматически определять ядро смаза даже для очень сложных случаев.
Возьмем фотоаппарат и сделаем смазанный снимок — благо для этого не требуется особенных усилий :)

Введем следующие обозначения:
B — наблюдаемое смазанное изображение
K — ядро размытия (траектория смаза), kernel
L — исходное неразмытое изображение (скрытое)
N — аддитивный шум
Тогда процесс смаза/искажения можно описать в виде следующего выражения
B = K*L+N
Где символ "*" это операция свертки, не путать с обычным умножением!
Что такое свертка, можно прочитать в первой части
В наглядном виде это можно представить следующим образом (опустив для простоты шумовую составляющую):

Так что же является наиболее сложным?
Представим себе простую аналогию — число 11 состоит из двух множителей. Каковы они?
Вариантов решения бесконечно:
11 = 1 x 11
11 = 2 x 5.5
11 = 3 x 3.667
и т.д.
Или, переходя к наглядному представлению:

Т.е. нужно больше информации. Одним из вариантов этого является задание целевой функции — это такая функция, значение которое тем выше (в простом случае), чем ближе получаемый результат к желаемому.
Исследования показали, что несмотря на то, что реальные изображения имеют большой разброс значений отдельных пикселей, градиенты этих значений имеют вид распределения с медленно убывающими границами (Heavy-tailed distribution). Такое распределение имеет пик в окрестности нуля и, в отличие от гауссового распределения, имеет значительно большие вероятности больших значений (вот такое масло масляное).
Это совпадает с интуитивным представлением, что на реальных изображениях в большинстве случаев присутствуют большие области более-менее постоянной яркости, которые заканчиваются объектами с резкими и средними перепадами яркости.
Вот пример гистограммы градиентов для резкого изображения:

И для размытого изображения:
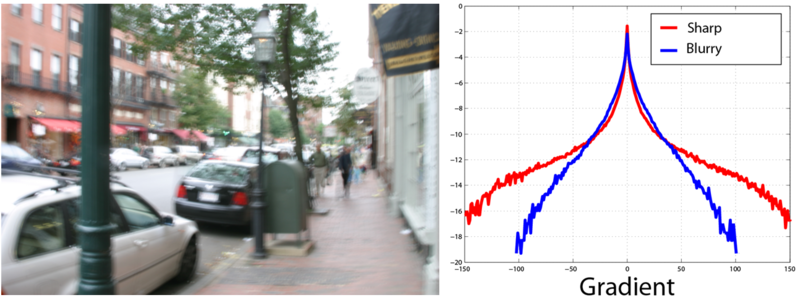
Таким образом мы получили инструмент, которые позволяет нам измерить «качество» получаемого результата с точки зрения четкости и похожести на реальное изображение.
Теперь мы можем сформулировать основные пункты для построение завершенной модели:
1. Ограничения накладываемые моделью искажения B = K*L+N
2. Целевая функция для результата реконструкции — насколько похожа гистограмма градиентов на теоретическое распределение с медленно убывающими границами. Обозначим ее как p(LP)
3. Целевая функция для ядра искажения — положительные значения и низкая доля белых пикселей (т.к. траектория смаза обычно представлена тонкой линией). Обозначим ее как p(K)
Объединим все это в общую целевую функцию следующим образом:

Где q(LP), q(K) распределения, получаемые подходом Variational Bayesian
Далее эта целевая функция минимизируется методом покоординатного спуска с некоторыми дополнениями, которые я не буду описывать из-за их сложности и обилия формул — все это можно прочитать в работе Фергуса.
Этот подход позволяет улучшить качество имеющегося ядра, но им нельзя построить это ядро с нуля, т.к. скорее всего в процессе нахождения решения мы попадем в один из локальных минимумов.
Вначале из входного размытого изображения мы строим пирамиду изображений с разным разрешением. От самого маленького размера до исходного размера.
Далее мы инициализируем алгоритм с помощью ядра размером 3*3 с одним из простых шаблонов — вертикальная линия, горизонтальная линия или гауссово пятно. В качестве универсального варианта можно выбрать последний — гауссово пятно.
Используя алгоритм оптимизации, описанный выше мы улучшаем оценку ядра, используя самый маленький размер изображения в построенной пирамиде.
После этого мы ресайзим полученное уточненное ядро до, скажем, 5*5 пикселей и повторяем процесс уже с изображением следующего размера.
Таким образом на каждом шаге мы чуть-чуть улучшаем ядро и в результате получаем весьма точную траекторию смаза.
Продемонстрируем итеративное построение ядра на примере.
Исходное изображение:

Процесс уточнения ядра:

Первая и третья строки показывают оценку ядра на каждом уровне пирамиды изображений.
Вторая и четвертая строки — оценка неискаженного изображения.
Результат:

Более современные подходы имеют примерно такую идею последовательного уточнения ядра, но используют более изощренные варианты целевой функции для результата реконструкции и ядра искажения. Плюс к этому осуществляют промежуточную и финальную фильтрацию получаемого ядра, чтобы убрать лишний шум и исправить некоторые ошибки в алгоритме уточнения.
Мы реализовали похожий вариант и добавили как новую функцию в SmartDeblur 2.0 — все по-прежнему бесплатно :)
Адрес проекта: smartdeblur.net
(Исходники и бинарники от предыдущей версии можно найти на GitHub: github.com/Y-Vladimir/SmartDeblur )
Пример работы:

Другой пример:
И в заключение, результат работы на изображении c конференции Adobe MAX 2011:
Как видно, результат практически идеален — почти как у Adobe в их демонстрации.
Позже увеличим его, после того как оптимизируем деконволюцию и пирамидальное построение.
Интерфейс выглядит следующим образом:

Для работы с программой требуется лишь загрузить изображение и нажать «Analyze Blur» и согласиться с выбором всего изображения — анализ может занят несколько минут. Если результат не устраивает, можно выбрать другой регион (выделить мышкой на изображении двигая ее вправо-вниз, немного не очевидно, но пока так :) ). Правой кнопкой выделение убирается.
Галочка «Agressive Detection» изменяет параметры, чтобы выделять только самые важные элементы ядра.
Пока что хорошие результаты достигаются далеко не на всех изображениях — поэтому будем очень рады фидбеку, это поможет нам улучшить алгоритмы!
Vladimir Yuzhikov (Владимир Южиков)
В большинстве случаев траектория смаза предполагается прямой линией, параметры которой должен задавать сам пользователь — для этого требуется достаточно кропотливая работа по подбору ядра, кроме того, в реальных фотографиях траектория смаза далека от линии и представляет собой замысловатую кривую переменной плотности/яркости, форму которой крайне сложно подобрать вручную.

В последние несколько лет интенсивно развивается новое направлении в теории восстановления изображений — слепая обратная свертка (Blind Deconvolution). Появилось достаточно много работ по этой теме, и начинается активное коммерческое использование результатов.
Многие из вас помнят конференцию Adobe MAX 2011, на которой они как раз показали работу одного из алгоритмов Blind Deconvolution: Исправление смазанных фотографий в новой версии Photoshop
В этой статье я хочу подробнее рассказать — как же работает эта удивительная технология, а также показать практическую реализацию SmartDeblur, который теперь тоже имеет в своем распоряжении этот алгоритм.
Внимание, под катом много картинок!
Начало
Этот пост является продолжением серии моих постов «Восстановление расфокусированных и смазанных изображений»:Часть 1. Теория — Восстановление расфокусированных и смазанных изображений
Часть 2. Практика — Восстановление расфокусированных и смазанных изображений
Часть 3. Повышаем качество — Восстановление расфокусированных и смазанных изображений
Рекомендуется прочитать хотя бы первую теоретическую часть, чтобы лучше понимать, что такое свертка, деконволюция, преобразование Фурье и прочие термины. Хоть я и обещал, что третья часть будет последней, но не смог удержаться и не рассказать про последние веяния в области восстановления изображений.
Я буду рассматривать Blind Decovolution на примере работы американского профессора Rob Fergus «Removing Camera Shake from a Single Photograph». Оригинал статьи можно найти на его страничке: http://cs.nyu.edu/~fergus/pmwiki/pmwiki.php
Это не самая новая работа, в последнее время появилось много других публикаций, которые демонстрируют лучшие результаты — но там используется совсем сложная математика ((для неподготовленного читателя) в ряде этапов, а основной принцип остается тем же. К тому же, работа Фергуса является своего рода «классикой», он одним из первых предложил принципиально новый подход, который позволил автоматически определять ядро смаза даже для очень сложных случаев.
Модель искажения
И так, приступим.Возьмем фотоаппарат и сделаем смазанный снимок — благо для этого не требуется особенных усилий :)

Введем следующие обозначения:
B — наблюдаемое смазанное изображение
K — ядро размытия (траектория смаза), kernel
L — исходное неразмытое изображение (скрытое)
N — аддитивный шум
Тогда процесс смаза/искажения можно описать в виде следующего выражения
B = K*L+N
Где символ "*" это операция свертки, не путать с обычным умножением!
Что такое свертка, можно прочитать в первой части
В наглядном виде это можно представить следующим образом (опустив для простоты шумовую составляющую):

Так что же является наиболее сложным?
Представим себе простую аналогию — число 11 состоит из двух множителей. Каковы они?
Вариантов решения бесконечно:
11 = 1 x 11
11 = 2 x 5.5
11 = 3 x 3.667
и т.д.
Или, переходя к наглядному представлению:

Целевая функция
Чтобы получить конкретное решение нужно вводить ограничения, как-то описывать модель того, к чему мы стремимся.Т.е. нужно больше информации. Одним из вариантов этого является задание целевой функции — это такая функция, значение которое тем выше (в простом случае), чем ближе получаемый результат к желаемому.
Исследования показали, что несмотря на то, что реальные изображения имеют большой разброс значений отдельных пикселей, градиенты этих значений имеют вид распределения с медленно убывающими границами (Heavy-tailed distribution). Такое распределение имеет пик в окрестности нуля и, в отличие от гауссового распределения, имеет значительно большие вероятности больших значений (вот такое масло масляное).
Это совпадает с интуитивным представлением, что на реальных изображениях в большинстве случаев присутствуют большие области более-менее постоянной яркости, которые заканчиваются объектами с резкими и средними перепадами яркости.
Вот пример гистограммы градиентов для резкого изображения:

И для размытого изображения:

Таким образом мы получили инструмент, которые позволяет нам измерить «качество» получаемого результата с точки зрения четкости и похожести на реальное изображение.
Теперь мы можем сформулировать основные пункты для построение завершенной модели:
1. Ограничения накладываемые моделью искажения B = K*L+N
2. Целевая функция для результата реконструкции — насколько похожа гистограмма градиентов на теоретическое распределение с медленно убывающими границами. Обозначим ее как p(LP)
3. Целевая функция для ядра искажения — положительные значения и низкая доля белых пикселей (т.к. траектория смаза обычно представлена тонкой линией). Обозначим ее как p(K)
Объединим все это в общую целевую функцию следующим образом:

Где q(LP), q(K) распределения, получаемые подходом Variational Bayesian
Далее эта целевая функция минимизируется методом покоординатного спуска с некоторыми дополнениями, которые я не буду описывать из-за их сложности и обилия формул — все это можно прочитать в работе Фергуса.
Этот подход позволяет улучшить качество имеющегося ядра, но им нельзя построить это ядро с нуля, т.к. скорее всего в процессе нахождения решения мы попадем в один из локальных минимумов.
Пирамидальный подход
Решением этой проблемы является итерационный подход к построению ядра искажения.Вначале из входного размытого изображения мы строим пирамиду изображений с разным разрешением. От самого маленького размера до исходного размера.
Далее мы инициализируем алгоритм с помощью ядра размером 3*3 с одним из простых шаблонов — вертикальная линия, горизонтальная линия или гауссово пятно. В качестве универсального варианта можно выбрать последний — гауссово пятно.
Используя алгоритм оптимизации, описанный выше мы улучшаем оценку ядра, используя самый маленький размер изображения в построенной пирамиде.
После этого мы ресайзим полученное уточненное ядро до, скажем, 5*5 пикселей и повторяем процесс уже с изображением следующего размера.
Таким образом на каждом шаге мы чуть-чуть улучшаем ядро и в результате получаем весьма точную траекторию смаза.
Продемонстрируем итеративное построение ядра на примере.
Исходное изображение:

Процесс уточнения ядра:

Первая и третья строки показывают оценку ядра на каждом уровне пирамиды изображений.
Вторая и четвертая строки — оценка неискаженного изображения.
Результат:

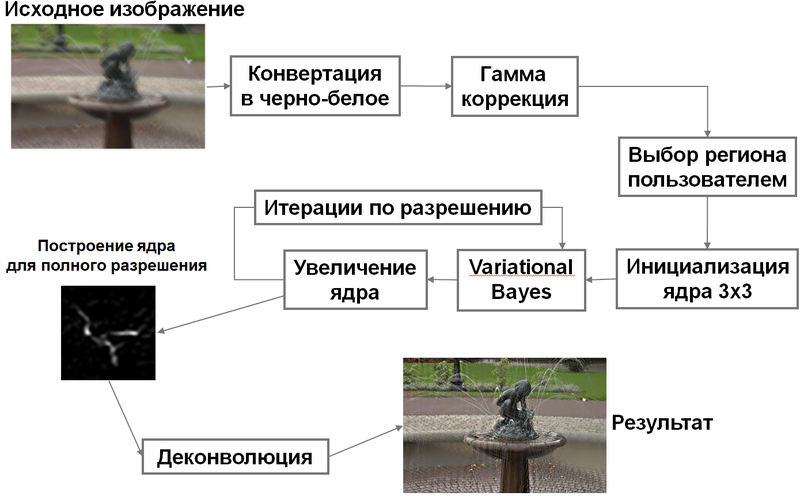
Блок-схема алгоритма
Осталось собрать все вместе и описать алгоритм целиком:
Более современные подходы имеют примерно такую идею последовательного уточнения ядра, но используют более изощренные варианты целевой функции для результата реконструкции и ядра искажения. Плюс к этому осуществляют промежуточную и финальную фильтрацию получаемого ядра, чтобы убрать лишний шум и исправить некоторые ошибки в алгоритме уточнения.
Практическая реализация
Наверное, самое интересное — это поиграться с алгоритмом Blind Deconvolution вживую на реальных изображениях!Мы реализовали похожий вариант и добавили как новую функцию в SmartDeblur 2.0 — все по-прежнему бесплатно :)
Адрес проекта: smartdeblur.net
(Исходники и бинарники от предыдущей версии можно найти на GitHub: github.com/Y-Vladimir/SmartDeblur )
Пример работы:

Другой пример:
 |
 |
 |
И в заключение, результат работы на изображении c конференции Adobe MAX 2011:
 |
 |
 |
Как видно, результат практически идеален — почти как у Adobe в их демонстрации.
Технические детали
Пока что максимальный размер обрабатываемого изображение установлен как 1200*1200. Это связано с тем, что алгоритмы потребляют очень много памяти. Даже на изображении 1000 пикселей — больше гигабайта. Поэтому введено ограничение на размер.Позже увеличим его, после того как оптимизируем деконволюцию и пирамидальное построение.
Интерфейс выглядит следующим образом:

Для работы с программой требуется лишь загрузить изображение и нажать «Analyze Blur» и согласиться с выбором всего изображения — анализ может занят несколько минут. Если результат не устраивает, можно выбрать другой регион (выделить мышкой на изображении двигая ее вправо-вниз, немного не очевидно, но пока так :) ). Правой кнопкой выделение убирается.
Галочка «Agressive Detection» изменяет параметры, чтобы выделять только самые важные элементы ядра.
Пока что хорошие результаты достигаются далеко не на всех изображениях — поэтому будем очень рады фидбеку, это поможет нам улучшить алгоритмы!
--Vladimir Yuzhikov (Владимир Южиков)
