Задачи на разрезание — это та область математики, где, как говорится, мамонт не валялся. Множество отдельных проблем, но по сути нет общей теории. Помимо всем известной теоремы Бойяи-Гервина, других фундаментальных результатов в этой области практически нет. Неопределённость — вечный спутник задач на разрезание. Мы можем, например, разрезать правильный пятиугольник на шесть частей, из которых можно сложить квадрат; однако мы не можем доказать, что пяти частей для этого было бы недостаточно.
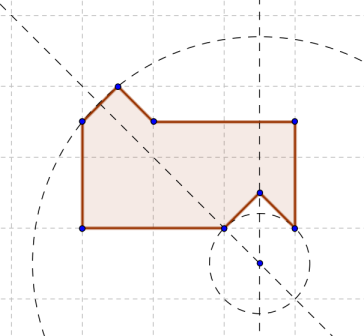
С помощью хитрой эвристики, воображения и поллитры нам порой удаётся найти конкретное решение, но, как правило, мы не обладаем подходящим инструментарием, чтобы доказать минимальность этого решения или же его несуществование (последнее, разумеется, относится к случаю, когда мы решение не нашли). Это печально и несправедливо. И как-то раз я взял чистую тетрадку и решил восстановить справедливость в масштабах одной конкретной задачи: разрезания плоской фигуры на две равных (конгруэнтных) части. В рамках этого цикла статей (их, кстати, будет три) мы с вами, камрады, рассмотрим вот этот забавный многоугольник, изображённый ниже, и попытаемся беспристрастно разобраться, можно ли разрезать его на две равных фигуры, или же таки нет.
Для начала освежим школьный курс геометрии и вспомним, что такое равные фигуры. Яндекс услужливо подсказывает:
Теперь расспросим Википедию про движения. Она расскажет нам, во-первых, что движение — это преобразование плоскости, которое сохраняет расстояния между точками. Во-вторых, там даже приведена классификация движений на плоскости. Все они относятся к одному из следующих трёх типов:
Введём некоторые обозначения. Разрезаемую фигуру мы будем называть фигурой A, а две гипотетеческих равных фигуры, на которые мы будто бы можем её разрезать, обзовём B и C соответственно. Часть плоскости, не занятую фигурой A, мы назовём областью D. В тех случаях, когда в качестве разрезаемой фигуры рассматривается конкретный многоугольник с картинки, мы будем называть его A0.
Так вот, если фигуру A можно разрезать на две равных части B и C, то существует движение, переводящее B в C. Это движение может быть либо параллельным переносом, либо поворотом, либо скользящей симметрией (начиная с этого момента, я больше не оговариваю, что зеркальная симметрия также считается скользящей). На этом нехитром и, я бы даже сказал, очевидном, базисе и будет строиться наше решение. В этой части мы рассмотрим самый простой случай — параллельный перенос. Поворот и скользящая симметрия попадут во вторую и третью часть соответственно.
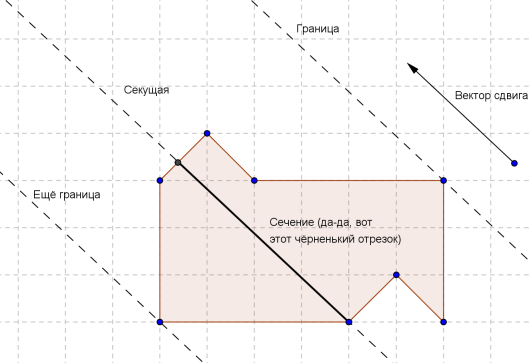
Параллельный перенос задаётся единственным параметром — вектором, на который происходит сдвиг. Введём ещё несколько терминов. Прямую, параллельную вектору сдвига и содержащую хотя бы одну точку фигуры A, будем называть секущей. Пересечение секущей прямой и фигуры A будем называть сечением. Секущую, относительно которой фигура A (за вычетом сечения) целиком лежит в одной полуплоскости, будем называть границей.
Лемма 1. Сечение границей должно содержать более одной точки.
Руководствуясь этой нехитрой леммой, нетрудно понять, что искомый параллельный перенос может происходить лишь вдоль вертикальной оси (в текущей ориентации картинки) Если бы он был в любом другом направлении, хотя бы одно из граничных сечений состояло бы из единственной точки. Это можно понять, мысленно повращав вектор сдвига и посмотрев, что при этом происходит с границами. Чтобы исключить случай вертикального параллельного переноса, нам понадобится более хитрый инструмент.
Лемма 2. Прообраз точки, находящейся на границе фигуры C, находится либо на границе фигур B и C, либо на границе фигуры B и области D.
Теорема 1. Если сечение фигуры A представляет собой отрезок, то его длина кратна длине вектора сдвига.
Следствие из теоремы 1. Любые два сечения, являющиеся отрезками, должны быть соизмеримы.
Используя это следствие, нетрудно показать, что вертикальный параллельный перенос тоже отпадает.
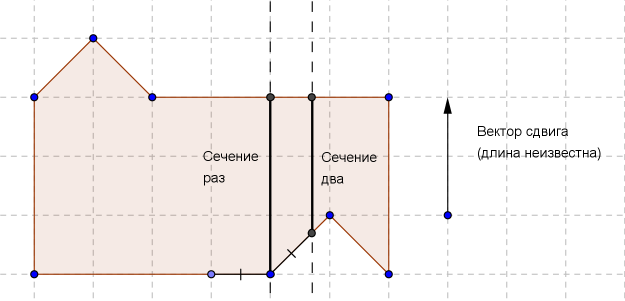
Действительно, сечение раз имеет длину три клетки, а сечение два — три минус корень из двух пополам. Очевидно, эти величины несоизмеримы.
Если фигуру A0 и можно разрезать на две равные фигуры B и C, то B не переводится в C параллельным переносом. Продолжение следует.
С помощью хитрой эвристики, воображения и поллитры нам порой удаётся найти конкретное решение, но, как правило, мы не обладаем подходящим инструментарием, чтобы доказать минимальность этого решения или же его несуществование (последнее, разумеется, относится к случаю, когда мы решение не нашли). Это печально и несправедливо. И как-то раз я взял чистую тетрадку и решил восстановить справедливость в масштабах одной конкретной задачи: разрезания плоской фигуры на две равных (конгруэнтных) части. В рамках этого цикла статей (их, кстати, будет три) мы с вами, камрады, рассмотрим вот этот забавный многоугольник, изображённый ниже, и попытаемся беспристрастно разобраться, можно ли разрезать его на две равных фигуры, или же таки нет.

Введение
Для начала освежим школьный курс геометрии и вспомним, что такое равные фигуры. Яндекс услужливо подсказывает:
Две фигуры на плоскости называются равными, если существует движение, взаимно однозначно переводящее одну фигуру в другую.
Теперь расспросим Википедию про движения. Она расскажет нам, во-первых, что движение — это преобразование плоскости, которое сохраняет расстояния между точками. Во-вторых, там даже приведена классификация движений на плоскости. Все они относятся к одному из следующих трёх типов:
- Параллельный перенос
- Поворот
- Скользящая симметрия (сюда я удобства ради и пользы для включаю зеркальная симметрию, как вырожденный случай, где параллельный перенос производится на нулевой вектор)
Введём некоторые обозначения. Разрезаемую фигуру мы будем называть фигурой A, а две гипотетеческих равных фигуры, на которые мы будто бы можем её разрезать, обзовём B и C соответственно. Часть плоскости, не занятую фигурой A, мы назовём областью D. В тех случаях, когда в качестве разрезаемой фигуры рассматривается конкретный многоугольник с картинки, мы будем называть его A0.
Так вот, если фигуру A можно разрезать на две равных части B и C, то существует движение, переводящее B в C. Это движение может быть либо параллельным переносом, либо поворотом, либо скользящей симметрией (начиная с этого момента, я больше не оговариваю, что зеркальная симметрия также считается скользящей). На этом нехитром и, я бы даже сказал, очевидном, базисе и будет строиться наше решение. В этой части мы рассмотрим самый простой случай — параллельный перенос. Поворот и скользящая симметрия попадут во вторую и третью часть соответственно.
Случай 1: параллельный перенос
Параллельный перенос задаётся единственным параметром — вектором, на который происходит сдвиг. Введём ещё несколько терминов. Прямую, параллельную вектору сдвига и содержащую хотя бы одну точку фигуры A, будем называть секущей. Пересечение секущей прямой и фигуры A будем называть сечением. Секущую, относительно которой фигура A (за вычетом сечения) целиком лежит в одной полуплоскости, будем называть границей.

Лемма 1. Сечение границей должно содержать более одной точки.
Доказательство: очевидно. Ну или более развёрнуто: докажем от противного. Если эта точка принадлежит фигуре B, то её образ (т.е. точка, в которую она перейдёт при параллельном переносе) принадлежит фигуре C => образ принадлежит фигуре A => образ принадлежит сечению. Противоречие. Если эта точка принадлежит фигуре C, то её прообраз (точка, которая при параллельном переносе перейдёт в неё) принадлежит фигуре B, и далее аналогично. Получается, в сечении должно быть хотя бы две точки.
Руководствуясь этой нехитрой леммой, нетрудно понять, что искомый параллельный перенос может происходить лишь вдоль вертикальной оси (в текущей ориентации картинки) Если бы он был в любом другом направлении, хотя бы одно из граничных сечений состояло бы из единственной точки. Это можно понять, мысленно повращав вектор сдвига и посмотрев, что при этом происходит с границами. Чтобы исключить случай вертикального параллельного переноса, нам понадобится более хитрый инструмент.
Лемма 2. Прообраз точки, находящейся на границе фигуры C, находится либо на границе фигур B и C, либо на границе фигуры B и области D.
Доказательство: неочевидно, но сейчас мы это исправим. Напомню, граничной точкой фигуры называется такая точка, что сколь угодно близко от неё найдутся как точки, принадлежащие фигуре, так и точки, не принадлежащие ей. Соответственно, вблизи граничной точки (назовём её O') фигуры C найдутся как точки фигуры C, так и другие точки, принадлежащие либо фигуре B, либо области D. Прообразами точек фигуры C могут быть только точки фигуры B. Следовательно, сколь угодно близко к прообразу точки O' (будет логично назвать его точкой O) найдутся точки фигуры B. Прообразами точек фигуры B могут быть любые точки, не принадлежащие B (то есть либо точки фигуры С, либо точки области D). Аналогично для точек области D. Следовательно, сколь угодно близко к точке O найдутся либо точки фигуры C (и тогда точка O будет на границе B и C), либо точки области D (и тогда прообраз на границе B и D). Если вы сумеете продраться через все эти буквы, то согласитесь, что лемма доказана.
Теорема 1. Если сечение фигуры A представляет собой отрезок, то его длина кратна длине вектора сдвига.
Доказательство: рассмотрим «дальний» конец этого отрезка (т.е. тот конец, прообраз которого также принадлежит отрезку). Этот конец, очевидно, принадлежит фигуре C и является её граничной точкой. Следовательно, его прообраз (кстати говоря, также лежащий на отрезке и отстоящий от образа на длину вектора сдвига) будет либо на границе B и C, либо на границе B и D. Если он на границе B и C, то возьмём также и его прообраз. Будем повторять эту операцию, пока очередной прообраз не перестанет быть на границе C и не окажется на границе D — а это произойдёт как раз на другом конце сечения. В результате мы получим цепочку прообразов, которые разбивают сечение на некоторое количество маленьких отрезочков, длина каждого из которых равняется длине вектора сдвига. Следовательно, длина сечения кратна длине вектора сдвига, ч.т.д.
Следствие из теоремы 1. Любые два сечения, являющиеся отрезками, должны быть соизмеримы.
Используя это следствие, нетрудно показать, что вертикальный параллельный перенос тоже отпадает.

Действительно, сечение раз имеет длину три клетки, а сечение два — три минус корень из двух пополам. Очевидно, эти величины несоизмеримы.
Вывод
Если фигуру A0 и можно разрезать на две равные фигуры B и C, то B не переводится в C параллельным переносом. Продолжение следует.