Недавно на Хабре в одной статье упомянули про вопрос «Что было бы с миром, если бы число Пи равнялось 4?» Я решил слегка поразмышлять на эту тему, используя некоторые (пусть и не самые обширные) знания в соответствующих областях математики. Кому интересно – прошу под кат.
Чтобы представить такой мир, нужно математически реализовать пространство с иным соотношением длины окружности к ее диаметру. Это я и попытался сделать.
Оговорим сразу, что рассматривать я буду только двумерные пространства. Почему? Потому что окружность, собственно, определена в двумерном пространстве (если рассмотреть размерность n>2, то отношение меры (n-1)-мерной окружности к ее радиусу даже не будет константой).
Так что для начала я попытался придумать хоть какое-то пространство, где Пи не равно 3.1415… Для этого я взял метрическое пространство с метрикой, в которой расстояние между двумя точками равно максимуму среди модулей разности координат (т.е. расстояние Чебышева).
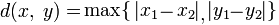
Какой же вид будет иметь единичная окружность в этом пространстве? Возьмем точку с координатами (0,0) за центр этой окружности. Тогда множество точек, расстояние (в смысле заданной метрики) от которых до центра равно 1, есть 4 отрезка, параллельных осям координат, образующих квадрат со стороной 2 и с центром в нуле.
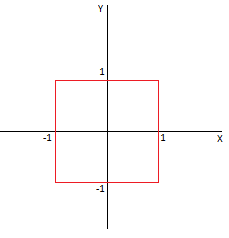
Да, в некоторой метрике это — окружность!
Посчитаем здесь Пи. Радиус равен 1, тогда диаметр, соответственно, равен 2. Можно также рассмотреть определение диаметра как наибольшего расстояния между двумя точками, но даже так оно равно 2. Осталось найти длину нашей «окружности» в данной метрике. Это сумма длин всех четырех отрезков, которые в данной метрике имеют длину max(0,2)=2. Значит, длина окружности равна 4*2=8. Ну а тогда Пи здесь равно 8/2=4. Получилось! Но нужно ли сильно радоваться? Результат этот практически бесполезен, ведь рассматриваемое пространство абсолютно абстрактно, в нем даже не определены углы и повороты. Вы можете представить себе мир, где по факту не определен поворот, и где окружностью является квадрат? Я пытался, честно, но у меня не хватило воображения.
Осознав, что я получил хоть и интересный, но абсолютно бесполезный (в смысле понимания строения мира с иным числом Пи) результат, я решил попытаться построить модель пространства с определенными понятиями углов и поворотов (то есть пространство с заданным невырожденным скалярным произведением). Разумеется, мне хотелось, чтобы метрика осталась метрикой в классическом понимании этого слова (т.е. чтобы расстояние между двумя точками было вещественным и неотрицательным). Но тогда скалярное произведение должно быть положительно определено, откуда вытекает, что пространство должно быть евклидовым. Или хотя бы локально евклидовым, то есть многообразием. Можно не забивать себе голову всеми этими понятиями, а просто читать дальше :)
Признаюсь, я убил некоторое время, пытаясь придумать хитрую евклидову метрику с нехорошим числом Пи. Я считал длины получившихся «окружностей», вспоминая различные интегральные формулы, пока до меня не дошел очевидный факт: если пространство евклидово, то заменой координат можно получить наше обычное пространство
, в котором число Пи известно. Значит и в другом евклидовом пространстве оно не изменит своего значения. Печаль.
Раз нам по-прежнему желательно наличие углов и поворотов, но евклидово пространство нас не устраивает, попробуем рассмотреть псевдоевклидово типа (1,1) (т.к. нас интересуют только двумерные). От обычного евклидового пространства оно отличается тем, что в нем квадрат расстояния между двумя точками (а, как следствие, и скалярное произведение двух векторов) может быть отрицательным. Чтобы особо не мучиться, я взял метрику в которой скалярное произведение в декартовых координатах будет иметь вид
. Какой же вид примет окружность единичного радиуса? Это будет множество точек, задаваемых уравнением 
, то есть… Гипербола.
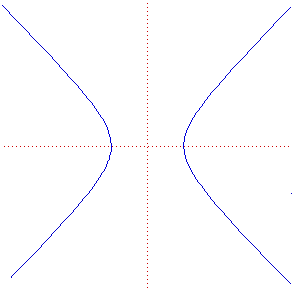
Да-да! В определенном пространстве и это — окружность.
Радиус равен 1, а вот с нахождением длины этой «окружности» есть некоторые сложности. После некоторых поисков информации в интернете, я пришел к выводу, что в псевдоевклидовом пространстве такое понятие как «число Пи» вообще не может быть определено, что, безусловно, плохо.
Если кто-нибудь в комментариях расскажет мне, как формально считать длину кривой в псевдоевклидовом пространстве, я буду очень рад, ибо моих познаний в дифференциальной геометрии, топологии (а также усердного гугления) для этого не хватило.
Не знаю, можно ли писать о выводах после таких не сильно продолжительных исследований, но кое-что сказать можно. Во-первых, попытавшись представить пространство с иным числом Пи, я понял, что оно будет слишком абстрактно, чтобы быть моделью реального мира. Во-вторых, когда если попытаться придумать более удачную модель (похожую на наш, реальный мир), выходит, что число Пи останется неизменным. Если принять за данность возможность отрицательного квадрата расстояния (что для обычного человека — просто абсурд), то Пи не будет определено вовсе! Все это и наводит на мысль, что, возможно, мира с другим числом Пи и вовсе быть не могло? Ведь не зря же Вселенная именно такая, какая она есть. А может быть, это и реально, только обычной математики, физики и человеческого воображения для этого недостаточно. А вы как считаете?
Upd. Узнал точно. Длина кривой в псевдоевклидовом пространстве может быть определена только на каком-либо его евклидовом подпространстве. То есть, в частности, для получившейся в попытке N3 «окружности» вовсе не определено такое понятие как «длина». Соответственно, Пи там тоже посчитать нельзя.
Чтобы представить такой мир, нужно математически реализовать пространство с иным соотношением длины окружности к ее диаметру. Это я и попытался сделать.
Попытка №1.
Оговорим сразу, что рассматривать я буду только двумерные пространства. Почему? Потому что окружность, собственно, определена в двумерном пространстве (если рассмотреть размерность n>2, то отношение меры (n-1)-мерной окружности к ее радиусу даже не будет константой).
Так что для начала я попытался придумать хоть какое-то пространство, где Пи не равно 3.1415… Для этого я взял метрическое пространство с метрикой, в которой расстояние между двумя точками равно максимуму среди модулей разности координат (т.е. расстояние Чебышева).
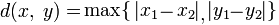
Какой же вид будет иметь единичная окружность в этом пространстве? Возьмем точку с координатами (0,0) за центр этой окружности. Тогда множество точек, расстояние (в смысле заданной метрики) от которых до центра равно 1, есть 4 отрезка, параллельных осям координат, образующих квадрат со стороной 2 и с центром в нуле.
Да, в некоторой метрике это — окружность!
Посчитаем здесь Пи. Радиус равен 1, тогда диаметр, соответственно, равен 2. Можно также рассмотреть определение диаметра как наибольшего расстояния между двумя точками, но даже так оно равно 2. Осталось найти длину нашей «окружности» в данной метрике. Это сумма длин всех четырех отрезков, которые в данной метрике имеют длину max(0,2)=2. Значит, длина окружности равна 4*2=8. Ну а тогда Пи здесь равно 8/2=4. Получилось! Но нужно ли сильно радоваться? Результат этот практически бесполезен, ведь рассматриваемое пространство абсолютно абстрактно, в нем даже не определены углы и повороты. Вы можете представить себе мир, где по факту не определен поворот, и где окружностью является квадрат? Я пытался, честно, но у меня не хватило воображения.
Попытка №2.
Осознав, что я получил хоть и интересный, но абсолютно бесполезный (в смысле понимания строения мира с иным числом Пи) результат, я решил попытаться построить модель пространства с определенными понятиями углов и поворотов (то есть пространство с заданным невырожденным скалярным произведением). Разумеется, мне хотелось, чтобы метрика осталась метрикой в классическом понимании этого слова (т.е. чтобы расстояние между двумя точками было вещественным и неотрицательным). Но тогда скалярное произведение должно быть положительно определено, откуда вытекает, что пространство должно быть евклидовым. Или хотя бы локально евклидовым, то есть многообразием. Можно не забивать себе голову всеми этими понятиями, а просто читать дальше :)
Признаюсь, я убил некоторое время, пытаясь придумать хитрую евклидову метрику с нехорошим числом Пи. Я считал длины получившихся «окружностей», вспоминая различные интегральные формулы, пока до меня не дошел очевидный факт: если пространство евклидово, то заменой координат можно получить наше обычное пространство
, в котором число Пи известно. Значит и в другом евклидовом пространстве оно не изменит своего значения. Печаль.Попытка №3.
Раз нам по-прежнему желательно наличие углов и поворотов, но евклидово пространство нас не устраивает, попробуем рассмотреть псевдоевклидово типа (1,1) (т.к. нас интересуют только двумерные). От обычного евклидового пространства оно отличается тем, что в нем квадрат расстояния между двумя точками (а, как следствие, и скалярное произведение двух векторов) может быть отрицательным. Чтобы особо не мучиться, я взял метрику в которой скалярное произведение в декартовых координатах будет иметь вид
. Какой же вид примет окружность единичного радиуса? Это будет множество точек, задаваемых уравнением 
, то есть… Гипербола.Да-да! В определенном пространстве и это — окружность.
Радиус равен 1, а вот с нахождением длины этой «окружности» есть некоторые сложности. После некоторых поисков информации в интернете, я пришел к выводу, что в псевдоевклидовом пространстве такое понятие как «число Пи» вообще не может быть определено, что, безусловно, плохо.
Если кто-нибудь в комментариях расскажет мне, как формально считать длину кривой в псевдоевклидовом пространстве, я буду очень рад, ибо моих познаний в дифференциальной геометрии, топологии (а также усердного гугления) для этого не хватило.
Выводы:
Не знаю, можно ли писать о выводах после таких не сильно продолжительных исследований, но кое-что сказать можно. Во-первых, попытавшись представить пространство с иным числом Пи, я понял, что оно будет слишком абстрактно, чтобы быть моделью реального мира. Во-вторых, когда если попытаться придумать более удачную модель (похожую на наш, реальный мир), выходит, что число Пи останется неизменным. Если принять за данность возможность отрицательного квадрата расстояния (что для обычного человека — просто абсурд), то Пи не будет определено вовсе! Все это и наводит на мысль, что, возможно, мира с другим числом Пи и вовсе быть не могло? Ведь не зря же Вселенная именно такая, какая она есть. А может быть, это и реально, только обычной математики, физики и человеческого воображения для этого недостаточно. А вы как считаете?
Upd. Узнал точно. Длина кривой в псевдоевклидовом пространстве может быть определена только на каком-либо его евклидовом подпространстве. То есть, в частности, для получившейся в попытке N3 «окружности» вовсе не определено такое понятие как «длина». Соответственно, Пи там тоже посчитать нельзя.
