Отношение между «чистыми» и «прикладными математиками» основаны на доверии и понимании. «Чистые математики» не доверяют «прикладным математикам», а «прикладные математики» не понимают чистых математиков.
Некоторое время назад я столкнулся с тем, что не смог найти доступных материалов, в которых на великом и могучем описывался бы метод погруженной границы. Если в кратце, то это метод вычислительной гидродинамики, который позволяет расчитывать обтекание достаточно сложных по форме и динамике объектов. Так вот русскоязычных публикаций на эту тему было крайне недостаточно. «Не беда, будем читать работы зарубежных коллег» — подумалось мне. Но и тут ждал небольшой подвох — все имеющиеся материалы и публикации по этому методу были очень теоретичны, а мне (не уверен, возможно это не только моя особенность) обычно сложно сделать переход от теоретических выкладок к более-менее рабочему воплощению в коде. Поэтому для таких же несчастных, что и я (и с некоторой долей надежды на советы от умудренных опытом личностей) я решил сделать краткое описание этого метода и предложить самый простой способ его реализации.
Я буду рассматривать только оригинальный метод Пескина, т.к. на мой взгляд он проще, чем метод фиктивных ячеек (ghost-cells), метод усеченных ячеек (cut-cells) и все прочие их модификации.
Итак, википедия говорит нам, что «метод погруженной границы» (immersed boundary method) — это подход к моделированию взаимодействия между жидкостью и обтекаемым объектом (т.к. часто применяется для моделирования тонких волокон в биологических системах, то иногда используют термин «fiber»). И это чертовски верно =)
Основная особенность данного подхода заключается в том, что вводятся две раздельные сетки для расчета течения жидкости (в эйлеровых координатах) и для расчета параметров погруженной границы (тех самых волокон-фибр в лагранжевых координатах). Это позволяет использовать для расчета жидкости простые сетки и быстрые вычислительные методы, перенося всю сложность моделирования на этап взаимодействия с погруженной границей.
С чисто теоретической точки зрения, такой фокус проделывается с помощью добавления в уравнение Навье-Стокса силы воздействия погруженной границы на жидкость (точнее, плотности силы):
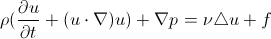
Эта сила некоторым некоторым образом вычисляется на основе расположения расчетных точек погруженной границы, и изменяет течение. Полная система уравнений выглядит так:
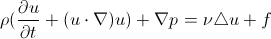
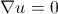
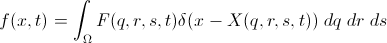
с краевыми условиями на погруженной границе, например, такого вида (условие прилипания aka «no-slip condition»):
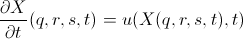
В этой системе уравнений
— есть переменные, которые описывают течение жидкости в области 
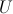с координатами 
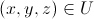, а 
— переменные, которые описывают состояние погруженной границы в области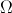 
с координатами 
.Собственно, взаимодействие жидкости и границы скрыто в последних двух уравнениях.
Если рассматривать все это безобразие с точки зрения реализации, то алгоритм для каждого шага по времени будет примерно следующим:
- В каждой точке погруженной границы вычисляем силу напряжения, исходя из ее текущего состояния
- Распределяем по некоторому алгоритму полученную силу на точки жидкости
- Вычисляем параметры течения жидкости с учетом полученной силы
- Интеполируем скорость из точек жидкости на узлы погруженной границы (из-за граничных условий скорость движения границы должна совпадать со скоростью жидкости)
- Изменяем положение узлов границы в соответствии со скоростью
Как можно заметить, в алгоритме есть два неопределенных момента — ничего не говориться о том, как именно определять силу напряжения, а также как вычислять параметры течения жидкости. В этом кроется серьезный плюс данного подхода — эти методы могут быть практически любыми =) Но чтобы быть более близким к реализации, мне придется как минимум рассказать о том, как же вычислять напряжение на границе (второй метод и правда можно выбрать произвольно, лишь бы он был достаточно точен).
На самом деле, крутые парни находят силу, которая образуется на границе, с помощью функционала энергии и учитывают силу растяжения и силу изгиба. Но к моему сожалению, я сам еще совершенно не разобрался с этим моментом. Поэтому можно схитрить и использовать менее точный, но достаточный для расчета метод штрафов (penalty method). Его суть проста — чем дальше граница отклонилась от своего первоначального положения, тем больше возникающая сила. В итоге необходимо только посчитать отклонение и умножить его на некоторый коэффициент жесткости, с которым можно поэксмериментировать.
Вторым тонким моментом в алгоритме является дельта-функция, которая фигурировала в системе уравнений. Нам необходимо иметь ее численный вариант и, по-хорошему, это целая песня, т.к. вариантов ее дискретизации огромная туча. Но в данном случае можно положиться на опыт коллег, которые советуют использовать такую (для трехмерного случая аналогично):
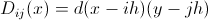
Теперь вместо тысячи слов можно описать получившийся алгоритм в виде кода.
Расчет напряжения на узлах может выглядеть примерно так:
for(int n = 0; n < boundary->nodes_count; ++n) {
Node *node = &boundary->nodes[n];
// get_area возвращает площадь поверхности, которая относится к данной точке
node->x_force = -boundary->stiffness * (node->x - node->x_ref) * boundary->get_area();
node->y_force = -boundary->stiffness * (node->y - node->y_ref) * boundary->get_area();
node->z_force = -boundary->stiffness * (node->z - node->z_ref) * boundary->get_area();
}
Распределение силы на точки жидкости:
for(int n = 0; n < boundary->nodes_count; ++n) {
// для узла границы находим ближайшую расчетную точку жидкости
int x_int = index(boundary->nodes[n].x, COORD_X);
int y_int = index(boundary->nodes[n].y, COORD_Y);
int z_int = index(boundary->nodes[n].z, COORD_Z);
// т.к. в дискретном варианте дельта-функции ненулевыми являются те узлы,
// которые находятся в двух шагах по сетке, то необходимо распределить силу
// на несколько (по две в каждую сторону) точек жидкости
for(int i = x_int-1; i <= x_int + 2; ++i) {
for(int j = y_int-1; j <= y_int + 2; ++j) {
for(int k = z_int-1; k <= z_int + 2; ++k) {
// находим расстояние от узла границы до текущей точки жидкости
long double dist_x = fabs(boundary->nodes[n].x - coord(i, COORD_X));
long double dist_y = fabs(boundary->nodes[n].y - coord(j, COORD_Y));
long double dist_z = fabs(boundary->nodes[n].z - coord(k, COORD_Z));
long double weight_x = delta(dist_x, COORD_X);
long double weight_y = delta(dist_y, COORD_Y);
long double weight_z = delta(dist_z, COORD_Z);
// прибавляем полученную силу к данной точке жидкости
force_X[i][j][k] += (boundary->nodes[n].x_force * weight_x * weight_y * weight_z) * boundary->get_area();
force_Y[i][j][k] += (boundary->nodes[n].y_force * weight_x * weight_y * weight_z) * boundary->get_area();
force_Z[i][j][k] += (boundary->nodes[n].z_force * weight_x * weight_y * weight_z) * boundary->get_area();
}
}
}
Любым угодным методом производим расчет течения. Затем интерполируем скорость на узлы жидкости:
for(int n = 0; n < boundary->nodes_count; ++n)
{
// по аналогии с силой, находим ближайщую точку
int x_int = index(boundary->nodes[n].x, COORD_X);
int y_int = index(boundary->nodes[n].y, COORD_Y);
int z_int = index(boundary->nodes[n].z, COORD_Z);
// и собираем скорость с ближайших точек
for(int i = x_int-1; i <= x_int + 2; ++i)
{
for(int j = y_int-1; j <= y_int + 2; ++j)
{
for(int k = z_int-1; k <= z_int + 2; ++k)
{
long double dist_x = fabs(boundary->nodes[n].x - coord(i, COORD_X));
long double dist_y = fabs(boundary->nodes[n].y - coord(j, COORD_Y));
long double dist_z = fabs(boundary->nodes[n].z - coord(k, COORD_Z));
long double weight_x = delta(dist_x, COORD_X);
long double weight_y = delta(dist_y, COORD_Y);
long double weight_z = delta(dist_z, COORD_Z);
boundary->nodes[n].x_vel += (velocity_U[i][j][k] * weight_x * weight_y * weight_z) * CB(Hx[i]);
boundary->nodes[n].y_vel += (velocity_V[i][j][k] * weight_x * weight_y * weight_z) * CB(Hy[j]);
boundary->nodes[n].z_vel += (velocity_W[i][j][k] * weight_x * weight_y * weight_z) * CB(Hz[k]);
}
}
}
}
Обновляем координаты узлов погруженной границы:
for(int n = 0; n < boundary->nodes_count; ++n)
{
boundary->nodes[n].x += boundary->nodes[n].x_vel;
boundary->nodes[n].y += boundary->nodes[n].y_vel;
boundary->nodes[n].z += boundary->nodes[n].z_vel;
}
Собственно, все. В данном подходе предполагается, что граница является гибкой, однако при достаточно высокой жесткости (она и правда должна быть огромной, учтите в экспериментах) можно симулировать поведение твердой границы.
Отмечу, что на данный момент для расчета течения жидкости я использую метод неполной аппроксимации минимальных невязок, а также приближаю исходную нестационарную проблему серией стационарных расчетов. Это, конечно, не самый лучший вариант, и делать так не стоит — но тем не менее он работает.
Все, отдаю этот текст на растерзание. Принимаются все рационализаторские замечания и предложения, т.к. работа еще очень далека от идеала.
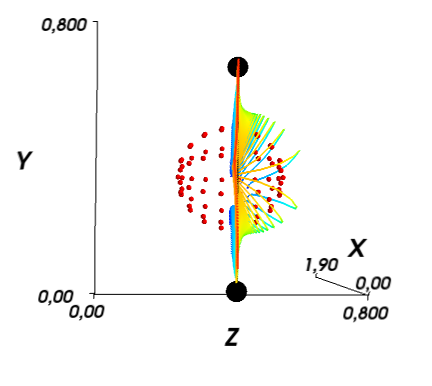
На закуску, несколько картинок с обтеканием сферы при достаточно высокой вязкости (и на достаточно грубой сетке).
