Comments 61
Этот метод годится только для монохромных изображений?
Интересно было бы копнуть в сторону более двух цветов.
Интересно было бы копнуть в сторону более двух цветов.
gpuhacks.wordpress.com/2013/07/08/signed-distance-field-rendering-of-color-bit-planes/
Идея та же, просто разные цвета сохраняются в разных картах. Можно развить идею и использовать все 4 канала текстуры (RGBA) для четырёх различных цветов и комбинировать всё это в шейдере. Естественно число цветов ограничено, как и в векторном редакторе: каждый контур может иметь либо свой цвет, либо градиент, либо текстуру. Кстати говоря, SDF с градиентом сочетается очень хорошо (в RGB храним градиент, в альфе — SDF).
Идея та же, просто разные цвета сохраняются в разных картах. Можно развить идею и использовать все 4 канала текстуры (RGBA) для четырёх различных цветов и комбинировать всё это в шейдере. Естественно число цветов ограничено, как и в векторном редакторе: каждый контур может иметь либо свой цвет, либо градиент, либо текстуру. Кстати говоря, SDF с градиентом сочетается очень хорошо (в RGB храним градиент, в альфе — SDF).
Это же идеальный метод для рендера шрифтов. Плюс получаем базу для создания шейдеров для всевозможных эффектов типа контуров, теней и свечения. Пойду впиливать в проект. Ведь можно заимствовать код? )
Годный пост. :) Пойду пилить в проект.
в С++ коде заметил дефайну с циклом. От неё можно было бы избавиться, если параметры функции объявить как constexpr (C++11).
в С++ коде заметил дефайну с циклом. От неё можно было бы избавиться, если параметры функции объявить как constexpr (C++11).
Учту, спасибо. На определённых тестах дефайн почему-то показал себя лучше, а больше я не разбирался. Хотя в этом define вроде не было цикла, о котором речь? Compare?
Да, Compare. Меня смутил do { } while. А ноль в конце я как-то не заметил. :)
Это старомодная сишная обёртка для дефайна, чтобы его без проблем можно было использовать как функцию. Но поскольку обещал привести пример на Си++, а тут помесь с Си — проверю производительность обоих вариантов.
Так, ассемблерный выхлоп inline ничем не отличается от define. Безо всяких cast. Не знаю, что на меня нашло…
Так, ассемблерный выхлоп inline ничем не отличается от define. Безо всяких cast. Не знаю, что на меня нашло…
Об inline дебагер не спотыкается, а вот с макоросами-псевдофункциями беда, да инлайновые шаблонные функции более громосткие (хотя как сказать — переходы строк экранировать хоть в них не нужно), но зато точно не предоставят сюрпризов при трассировке.
Я «за» inline всеми конечностями. В конкретно данном случае в define не было необходимости, а кажущийся прирост производительности скорее всего был ошибкой. Возможно я static или inline забыл в тот момент дописать или ещё чего. Пофиксил код в посте, чтобы никого не смущать больше.
А у меня редактор это автоматически делает:) Вот и не лень было этим заниматься.
хотя как сказать — переходы строк экранировать хоть в них не нужно
А у меня редактор это автоматически делает:) Вот и не лень было этим заниматься.
Я правильно понял что под «векторностью» тут подразумевают двухцветность?
Под «векторностью» понимается shape — т. е. форма или контур. Задача раскрашивания контура — это уже тема целой отдельной статьи.
Т.е. к векторной графике, векторизации растра, когда картинка в итоге получается запомнена как массив из отрезков, сплайнов и т.п. точек с и их координатами, эта «векторность» отношения не имеет, и речь целиком и полностью только про растр? Откуда тут пошла векторность?
Картинка сохраняется в формате, который ближе всего видеокартам — в виде растрового изображения, но из неё восстанавливается растровый контур любого разрешения без потерь качества. Если совсем свысока взглянуть на любой векторный формат — это математическое описание изображения, по которому можно восстановить растр с любым требуемым разрешением. А кто сказал, что матрица интенсивностей, положенная в основу метода — не математическое описание?:) К сложившемуся термину «вектор» как набору кривых это конечно не имеет отношения.
А зачем здесь
Вы множите на 0.3? Получается если текстура 256х128 вы будете использовать только треть текстуры.
texture2D(tex,gl_FragCoord.xy/vec2(256., 128.)*.3Вы множите на 0.3? Получается если текстура 256х128 вы будете использовать только треть текстуры.
Это масштаб — текстура растягивается как раз на эту треть с целью демонстрации отсутствия искажений при масштабировании. В данном случае мы увидим только кошачий хвост. Почему в примерах такие дикие цифры? Я тестировал в онлайн-редакторе Kick.js, подбирая значения, что называется, «на лету».
Ну тогда бы могли продефайнить/юниформом сделать с соответствующим именем, раз уж все равно множите.
И честно говоря, я все равно не могу увидеть в «простейшем варианте» ничего кроме выборки «темноты» пикселя, и его обработки контрастом. За счёт сильного контраста выделяются линии. Возможно все правильно, я просто не понял алгоритма работы.
В том же kick.js есть кнопочка «Share» можете добавить «живые» примеры к статье (как я понял с текстурами).
И честно говоря, я все равно не могу увидеть в «простейшем варианте» ничего кроме выборки «темноты» пикселя, и его обработки контрастом. За счёт сильного контраста выделяются линии. Возможно все правильно, я просто не понял алгоритма работы.
В том же kick.js есть кнопочка «Share» можете добавить «живые» примеры к статье (как я понял с текстурами).
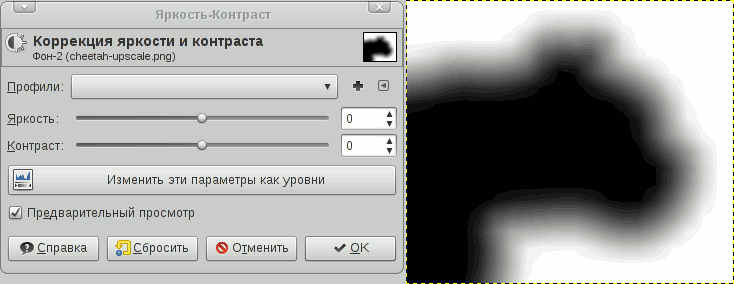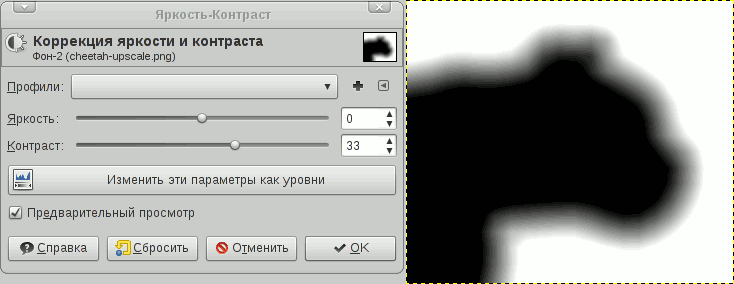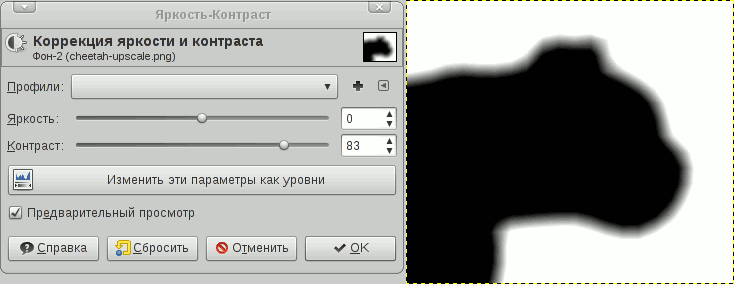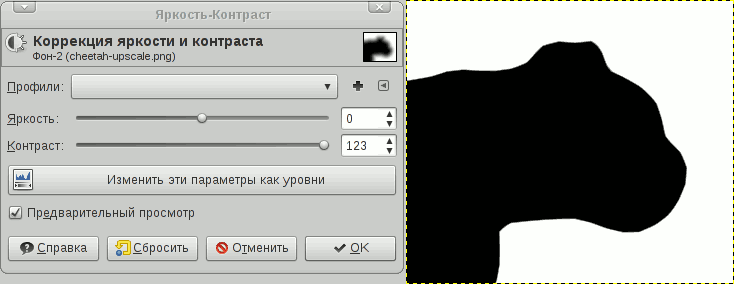
Алгоритм шейдера в общем виде и есть повышение контраста. Контраст повышается настолько, чтобы контур был сглаженным (эффект антиалиасинга). Аналогичную процедуру можно провернуть над SDF-картой в каком-нибудь ГИМПе. Откройте SDF, увеличьте контраст — это и будет результат работы шейдера.
А для этого там надо регистрироваться:)
В том же kick.js есть кнопочка «Share»
А для этого там надо регистрироваться:)
Что-то не очень понятно, что значит получить «векторную графику на видеоускорителе»? Я так понял, оригинальное изображение растровое. И не могли бы вы объяснить, каким образом после фактически размытия изображения после увеличения в 30 раз оно оказалось четче, чем оригинальное (картинка в начале)?
Если говорить максимально простым языком, то информация о контуре изображения была закодирована не одним пикселом, а группой пикселей на некоторой площади. Вот так и получается, что особым образом обрабатывая такую группу пикселей можно получить достаточно четкий контур более высокого разрешения.
Вот зарегистрируется автор на kick.js, добавит живой пример и увидите :)
Когда вы текстуру разрешением 64х64 пытаетесь растянуть до 640х640, каждый пиксель который отобразится на экране линейно интерполируется между двумя ближайшими пикселями, которые есть в текстуре. Допустим, вам необходимо получить цвет 175 пикселя по горизонтали (и какого то там по вертикали). Для этого 640 / 64 = 10 (каждый 10*i-й пиксель для 640х640 это i-й пиксель 64х64). 175/10 = 17,5 Целая часть 17, значит из текстуры берем цвет 17го пикселя, и 18 го, и смешиваем их в пропорции 0,5 (дробная часть). [Математически это все в 2-3 операции происходит]
А если есть линейная интерполяция, есть градиент, а значит есть размытие.
А размытие есть ни что иное как плавный переход от одного цвета к другому.
Разность свечения между самим ярким и самым темным пикселем — есть контраст.
Увеличивая контрастность изображения мы теряем оттенки (градиент/размытость), но тем самым увеличиваем четкость. И казалось бы должны снова появится кубики, но вместо них мы видим линии — это потому что цвета все же интерполируются.
По сути можно те же фокусы и с обычной монохромной картинкой проделывать. Но без размытости контуры будут выглядеть чересчур зубчато.
И я в общем-то согласен, что это ни какая не векторная графика, а растр.
Когда вы текстуру разрешением 64х64 пытаетесь растянуть до 640х640, каждый пиксель который отобразится на экране линейно интерполируется между двумя ближайшими пикселями, которые есть в текстуре. Допустим, вам необходимо получить цвет 175 пикселя по горизонтали (и какого то там по вертикали). Для этого 640 / 64 = 10 (каждый 10*i-й пиксель для 640х640 это i-й пиксель 64х64). 175/10 = 17,5 Целая часть 17, значит из текстуры берем цвет 17го пикселя, и 18 го, и смешиваем их в пропорции 0,5 (дробная часть). [Математически это все в 2-3 операции происходит]
А если есть линейная интерполяция, есть градиент, а значит есть размытие.
А размытие есть ни что иное как плавный переход от одного цвета к другому.
Разность свечения между самим ярким и самым темным пикселем — есть контраст.
Увеличивая контрастность изображения мы теряем оттенки (градиент/размытость), но тем самым увеличиваем четкость. И казалось бы должны снова появится кубики, но вместо них мы видим линии — это потому что цвета все же интерполируются.
По сути можно те же фокусы и с обычной монохромной картинкой проделывать. Но без размытости контуры будут выглядеть чересчур зубчато.
И я в общем-то согласен, что это ни какая не векторная графика, а растр.
Т.е., насколько я понимаю, мы вначале размываем изображение, делая линию контура так сказать, «срединной линией» размывки, потом увеличиваем изображение. Так как изображение размыто, лесенки становятся не так заметны, потому что при увеличении разрешения, грубо говоря, интерполируются не яркости 0 и 100 с шагом 10, а яркости 50 и 60 с шагом 1. А так как при увеличении «срединная линия» никуда не сдвинулась, мы потом, повышая контрастность, все пиксели, которые отличаются от нее на, предположим, -2 градации (т.е. темнее, они оказались внутри контура пумы) делаем черными, а которые на +2 градации (чуть светлее, снаружи контура) — светлыми.
Причем, если бы мы растягивали оригинальное изображение, то ввиду шага в 10 градаций яркости мы не смогли бы подойти к границе на 2 градации — либо на 10б либо на 0.
Причем, если бы мы растягивали оригинальное изображение, то ввиду шага в 10 градаций яркости мы не смогли бы подойти к границе на 2 градации — либо на 10б либо на 0.
То есть, увеличивая мелкое монохромное изображение, есть резон его перед увеличением размыть хитрым способом, а после увеличения вернуть контраст, вместо того, чтобы просто увеличить? Контур получается более гладкий?
Можно увеличить обычное изображение с альфа-каналом и потом увеличить контрастность, чтобы скрыть артефакты интерполяции, но есть два НО:
Подробнее об этих артефактах и недостатках можно посмотреть в оригинальной публикации Valve (есть в конце статьи). Описываемая техника позволяет сильно уменьшить оригинальное изображение по сравнению с оригиналом (экономия видеопамяти) и масштабировать как «вверх» так и «вниз» без значительных искажений. Контур при этом получается плавным и чётким с бесплатным антиалиасингом.
- при уменьшении того же изображения будут видны эффекты «лесенки» из-за особенностей интерполяции;
- при увеличении изображения появится крупная заметная «лесенка» опять же из-за особенностей интерполяции на видеокартах.
Подробнее об этих артефактах и недостатках можно посмотреть в оригинальной публикации Valve (есть в конце статьи). Описываемая техника позволяет сильно уменьшить оригинальное изображение по сравнению с оригиналом (экономия видеопамяти) и масштабировать как «вверх» так и «вниз» без значительных искажений. Контур при этом получается плавным и чётким с бесплатным антиалиасингом.
Я думаю, важно будет заметить, что алгоритм, используемый в статье, может делать ошибки в определении расстояний до ближайших черных пикселей. Его ошибки оцениваются вот в этой статье (Table II, колонка SWEDT). Причина для ошибок, насколько я понимаю, в том, что в доказательстве у авторов статьи [2] в вашем списке есть ошибка: в разделе 4 (доказательство) они предполагают, что ближайший черный пиксель для соседа будет таким же, как у текущего пикселя. Что, очевидно, не так.
И еще вы пишете «Зачем нужно прибавить единицу — не спрашивайте, результат эмпирический и без него получается криво». Возможно (хотя я внимательно не считал), это потому, что вы добавляете границу шириной в один пиксель перед работой алгоритма.
Это точно не из-за границы. Ошибку с единицей я заметил ещё раньше ошибки с однопиксельным бордюром (спасибо матрице самсунга:). Получается едва заметный перепад яркости. А однопиксельный бордюр нужен 1) для производительности 2) для того, чтобы примыкающие к краю контуры не засвечивались (очень сложно объяснить этот эффект, его тоже сложно заметить на глаз). Ещё более странно то, что единицу надо прибавить до извлечения квадратного корня. Тут уже нужно лезть в дебри доказательства, которое я признаться читал по диагонали.
По поводу ошибки в алгоритме — спасибо, добавил в статью. Не думал, что спустя 10 лет вышел «апдейт» публикации. Видно, что простора для развития идеи ещё очень много.
По поводу ошибки в алгоритме — спасибо, добавил в статью. Не думал, что спустя 10 лет вышел «апдейт» публикации. Видно, что простора для развития идеи ещё очень много.
Замечу, что этот апдейт вышел все-таки через 5 лет, не через 10 и, кроме того, это статья от других авторов.
После прочтения вашей статьи я осознал, что именно эту задачу мне предстоит решить в течение ближайших дней (но в 3D)—спасибо вам огромное за статью!—поэтому я немного почитал научные статьи по этой теме. Это оказалась довольно обширная область. И вот что я нашел: есть два очень неплохих обзора алгоритмов EDT: 2008 года и 2011 года.
В обзоре 2008 года рассматриваются только точные алгоритмы, поэтому вашего нет. В нем можно сразу перейти к заключению: из точных быстрее всего (и примерно одинаково) работают алгоритмы Maurer'а и Meijster'а. Алгоритм Маурера, судя по всему, очень сложный для реализации, а вот алгоритм Мейстера выглядит очень привлекательным.
В обзоре 2011 есть точные и неточные алгоритмы. В обзоре самые ценные—таблица 3 и картинка 4. Тот алгоритм, что вы используете, назыавется там EDT-2, он действительно дает ошибки. Что интересно, авторы показывают, что этот алгоритм работает медленне алгоритма Маурера (и, соответственно, Мейстера). Там представлен еще один точный алгоритм поновее—LLT, он описан в этой статье. Но он реально сложный (преобразования Лежандра, то-се) и лишь чуть-чуть быстрее алгоритма Маурера (и, соответственно, Мейстера). Авторы рассматривают еще один супер-алгоритм, FEED, но если присмотреться, то это алгоритм самих авторов, и он не очень популярен. Его основной недостаток—нужно заранее знать или оценить максимальную euclidean distance в картинке (чем она меньше, тем он быстрее). Поэтому его можно не рассматривать :-).
Исходя из всего этого, лично я пока собираюсь остановиться на алгоритме Мейстера. Может быть, еще посмотрю внимательнее на LLT. И может быть, даже опубликую отдельный пост с этими изысканиями.
P.S. В статье про LLT есть еще один алгоритм, NEP, быстрее чем LLT, но он, если почитать, будет работать только с выпуклыми объектами на картинке, так что в общем случае не подходит.
После прочтения вашей статьи я осознал, что именно эту задачу мне предстоит решить в течение ближайших дней (но в 3D)—спасибо вам огромное за статью!—поэтому я немного почитал научные статьи по этой теме. Это оказалась довольно обширная область. И вот что я нашел: есть два очень неплохих обзора алгоритмов EDT: 2008 года и 2011 года.
В обзоре 2008 года рассматриваются только точные алгоритмы, поэтому вашего нет. В нем можно сразу перейти к заключению: из точных быстрее всего (и примерно одинаково) работают алгоритмы Maurer'а и Meijster'а. Алгоритм Маурера, судя по всему, очень сложный для реализации, а вот алгоритм Мейстера выглядит очень привлекательным.
В обзоре 2011 есть точные и неточные алгоритмы. В обзоре самые ценные—таблица 3 и картинка 4. Тот алгоритм, что вы используете, назыавется там EDT-2, он действительно дает ошибки. Что интересно, авторы показывают, что этот алгоритм работает медленне алгоритма Маурера (и, соответственно, Мейстера). Там представлен еще один точный алгоритм поновее—LLT, он описан в этой статье. Но он реально сложный (преобразования Лежандра, то-се) и лишь чуть-чуть быстрее алгоритма Маурера (и, соответственно, Мейстера). Авторы рассматривают еще один супер-алгоритм, FEED, но если присмотреться, то это алгоритм самих авторов, и он не очень популярен. Его основной недостаток—нужно заранее знать или оценить максимальную euclidean distance в картинке (чем она меньше, тем он быстрее). Поэтому его можно не рассматривать :-).
Исходя из всего этого, лично я пока собираюсь остановиться на алгоритме Мейстера. Может быть, еще посмотрю внимательнее на LLT. И может быть, даже опубликую отдельный пост с этими изысканиями.
P.S. В статье про LLT есть еще один алгоритм, NEP, быстрее чем LLT, но он, если почитать, будет работать только с выпуклыми объектами на картинке, так что в общем случае не подходит.
Спасибо за детальный обзор статей по теме:) В статье, которую я смотрел стояла дата 2003 год. Наверное, есть эффективные алгоритмы (есть один с учетом антилалиасинга, который я представил в ссылках), но это всё делалось в рамках OpenSource проекта генератора шрифтов UBFG, поэтому я не сильно вдавался в детали алгоритмов или сравнительный анализ. Если получится сделать быстрее — contributions are welcome:) Когда я делал этот алгоритм для UBFG, я просто задумался, а можно ли это сделать имеющимися OpenSource средствами? Оказалось, что ImageMagick умеет это делать, скорость и качество для большинства разработчиков являются приемлемыми.
P.P.S. Совсем забыл: у обзора 2008 года есть сопутствующий сайт с картинками и исходным кодом.
Что только не придумают, — лишь бы аппаратно векторную графику не реализовывать!
А каким образом можно аппаратно реализовать векторную графику? Может, подкините статей?
www.khronos.org/openvg/
Зря иронизируете, уже целый стандарт есть, причём ему сто лет. NVIDIA тоже что-то пилит. Но опять же это не совсем аппаратная реализация, как и OpenGL, а стандарт. Тот же OpenGL имеет кучу нюансов, аппаратно может поддерживаться лишь операция рисования точек и линий, а остальные недостающие части стандарта реализует драйвер.
Зря иронизируете, уже целый стандарт есть, причём ему сто лет. NVIDIA тоже что-то пилит. Но опять же это не совсем аппаратная реализация, как и OpenGL, а стандарт. Тот же OpenGL имеет кучу нюансов, аппаратно может поддерживаться лишь операция рисования точек и линий, а остальные недостающие части стандарта реализует драйвер.
Ну почему же сразу иронизирую :) Тема-то интересная, вот и хочется узнать побольше. Спасибо, кстати за ссылку. Однако, назвать это аппаратной векторной графикой у меня язык не поворачивается. Ведь, насколько я понял, это всего лишь расширенные операции по рисованию кривых Безье и заливке фигур в дополнение к операциям рисования точек и линий. Чем оно отличается от того же OpenGL, в котором всё это давно уже есть, мне пока решительно не понятно.
Чем оно отличается от того же OpenGL, в котором всё это давно уже есть, мне пока решительно не понятно.
Да собственно ничем. Аппаратных устройств такого рода я пока не встречал (но возможно они существуют, в рамках каких-то специализированных приложений). Дело Кроноса — дать стандарт, а как его будут реализовывать — через OpenGL или аппаратно — головная боль производителей.
Почти все андроиды поддерживают openVG. И это именно аппаратное решение. Фактически openVG нужны те же наборы команд что и для OpenGL (те что в шейдере). В OpenGL ничего нет — в том то и дело. Кривую вы в нем просто так не нарисуете, заливка тела фигуры — будьте добры триангулировать… и т.д. openVG же, напротив, все это делает.
Можно попробовать вершинный шейдер написать, чтобы делал триангуляцию специально подготовленных полигонов, точно как упоминаемая ниже разработка NVideo, суть которой сводится к триангуляции кривых безье на GPU и заливка получившихся фигур градиентами и сплошными цветами, — ну а что еще надо!?
Проблема конечно отраслевая, не то чтобы техническая…
Проблема конечно отраслевая, не то чтобы техническая…
Там не вершинный шейдер и не триангуляция. Там пиксельным шейдером по квадратической/кубической формуле определяется принадлежность текущего пикселя телу или нет. Похоже вы бегло ознакомились со статьей и прочитали только «специальный случай» для которого требовалась триангуляция (разбиение одной кривой в треугольнике на 2 меньших).
И вообще — как это на вершинном шейдере возможно выполнить триангуляцию?
Наверное, автор хотел сказать, в геометрическом шейдере? Там можно, если мне не изменяет память. Но если я правильно понял предлагаемый метод, триангуляцию вообще можно делать на CPU, треугольники играют роль узлов кривых, а интерполяция — в фрагментном шейдере.
Совершенно верно, за исключением того что без триангуляции в 90% можно обойтись. Она нужна только когда одна кривая накладывается на другую. В фрагментном шейдере не совсем интерполяция, скорее там именно построение самой кривой. В упрощенном виде там так
Что есть решение уравнение параболы y = x^2 (квадратическая кривая)
if (texCoord.y-texCoord.x*texCoord.x > 0) discard;Что есть решение уравнение параболы y = x^2 (квадратическая кривая)
Под триангуляцией наверное тут следует понимать перевод кривых Безье в треугольники с учётом заполнения контура. Не исключено, что можно в офф-тайме как и в случае с SDF «запекать» растровые контуры. Остаётся главная проблема — антиалиасинг, что будет нагрузкой на фрагментный шейдр.
Кривая — это точка начала и конца, и одна опорная. Это и есть треугольник — никакой триагуляции.
Исключено — нельзя «запекать». Разве что будете рисовать в фрейм буфер с целью получения текстуры :)) Зачем их запекать?? Одно умножение куда быстрее выборки из текстуры.
Антиалиасинг в статье также детально описан.
Похоже никто не читает ссылок которые дает
Исключено — нельзя «запекать». Разве что будете рисовать в фрейм буфер с целью получения текстуры :)) Зачем их запекать?? Одно умножение куда быстрее выборки из текстуры.
Антиалиасинг в статье также детально описан.
Похоже никто не читает ссылок которые дает
Это не моя ссылка:) Про «запекание» я имел ввиду полученные треугольники сохранять в виде меша — это гораздо компактнее, чем тот же SDF, к тому же их не обязательно грузить в видеопамять. Но треугольники как-то надо получить из исходного вектора (SVG например). Метод растеризации более-менее понятен, а вот как этот набор треугольников получить? Сразу встаёт вопрос синтезирующего софта. Я всё-таки так понимаю часть треуглольников — «внутренние» — получены как раз триангуляцией, а другая часть — внутренний и внешний вектор, к которому и применяется описываемый алгоритм. Поправьте если мой английский совсем плох:
Next, we triangulate the interior of the closed path and form a triangle for each quadratic Bézier curve.
суть которой сводится к триангуляции кривых безье на GPU
Я говорю об этом. Нет там никакой триангуляции кривых безье. Есть триангуляция тела фигуры, мноугольника, SVG path…. Сами кривые не триангулируются (если только не попадают под тот случай когда один треугольник с кривой пересекает другой). Автор наверное представил себе, что кривая строится из множества линий, кои и триангулируются в вершинном (!) шейдере.
Я невнимательно читал, или в статье не описано, как по полученному SDF получить собственно отмасштабированную картинку?
Собственно, в статье есть примеры шейдеров на GLSL. Рисуем картинку любого размера с этим шейдером — из-за интерполяции текстур и выкручивания контраста получаем четкую и гладкую картинку.
Построение SDF объяснялось алгоритмически и затем был приведён пример кода — совершенно верный подход. Для восстановление картинки был приведён только фрагмент кода, без объяснений? Нелогично.
Вообще верное замечание, но алгоритм восстановления картинки из SDF-карты тривиален: увеличиваем или уменьшаем масштаб SDF-карты (хоть на 1600%) и увеличиваем контрастность до значения, позволяющего увидеть четкий контур с антиалиасингом. Это можно проделать в любом графическом редакторе, просто я данный момент не проиллюстрировал и упомянул вскользь:
Степень изменения контраста линейно зависит от масштаба и степени расплывчатости исходника, простыми словами, проще подогнать.
Здесь просто вытягиваем контраст относительно среднего значения (0.5).
Степень изменения контраста линейно зависит от масштаба и степени расплывчатости исходника, простыми словами, проще подогнать.
Ну, я почти уверен, что если прочитать всю статью и заодно ссылки, то этот момент дествительно станет тривиален. Но вы же понимаете, что в нашем мире тексты в интернете читаются по-другому. Быстро, по поверхности, понять о чём пишут. Картинки с SDF дают возможность за пару мгновений осознать сущность преобразования. Картинка с восстановлением и обозначенной линией контура на фоне отмасштабированного SDF позволила бы за пару мгновений осознать шаг реконструкции.
Это одна из модификаций грубого CDA — 8SSEDT. Основная идея — храним дельту по X и Y до ближайшего соседа. По этой дельте мы сможем рассчиатать правильную дистанцию
CDA считает по красной ломаной линии, т.к. просто складывает расстояния на итерациях

а 8SSEDT вычисляет честно гипотенузу.
У вас не приведено откуда берется вот такая «магия»:
Я хочу объяснить. Так как мы храним дельты по осям: dx и dy, а сравнивать нам нужно дистанцию (и записывать минимальную), то нам придется каждый раз вычислять квадрат расстояния dx*dx+dy*dy, чтобы мы могли его сравнить. Авторы решили сэкономить на этом. Для этого они дополинтельно решили хранить квадрат расстояния. Т.е. теперь каждый пиксель несет в себе (dx, dy, Distance^2). Ок, для соседей теперь мы не будем считать расстояние, но мы будем считать новое расстояние каждый раз, когда будем записывать его в текущий пиксель. Авторы соптимизировали и эту часть:
Пусть новый пиксель у нас находится в координатах (dx+1, dy). Квадрат расстояния до него будет (dx+1)^2+dy^2 = dx*dx + 2*dx + 1 + dy*dy = (dx*dx + dy*dy) + 2*dx + 1
А поскольку (dx*dx + dy*dy) = старое расстояние Distace^2, то можно к нему просто прибавить 2*dx + 1, чтобы получить новую дистанцию.
Вот откуда взялось 2 * q.x + 1 и 2 * (q.x + q.y + 1)
А теперь суть. Данный подход выливается вот в такую реализацию:
Так как алгоритм писался в бородатые годы, то ради экономии операций тут куча ветвлений, и как результат — потенциальных ошибок branch prediction. Мне кажется гораздо быстрее будет подсчитать квадрат расстояния налету:
А так же возможно будет быстрее вообще избавиться от хранения квадрата дистанции в изображении. Выкидываем поле f из структуры:
а функцию Compare переписываем вот так:
CDA считает по красной ломаной линии, т.к. просто складывает расстояния на итерациях

а 8SSEDT вычисляет честно гипотенузу.
У вас не приведено откуда берется вот такая «магия»:
h(p, q) {
if q - сосед 1 или 5 {return 2 * q.x + 1}
if q - сосед 3 или 7 {return 2 * q.y + 1}
в остальных случаях {return 2 * (q.x + q.y + 1)}
}
Я хочу объяснить. Так как мы храним дельты по осям: dx и dy, а сравнивать нам нужно дистанцию (и записывать минимальную), то нам придется каждый раз вычислять квадрат расстояния dx*dx+dy*dy, чтобы мы могли его сравнить. Авторы решили сэкономить на этом. Для этого они дополинтельно решили хранить квадрат расстояния. Т.е. теперь каждый пиксель несет в себе (dx, dy, Distance^2). Ок, для соседей теперь мы не будем считать расстояние, но мы будем считать новое расстояние каждый раз, когда будем записывать его в текущий пиксель. Авторы соптимизировали и эту часть:
Пусть новый пиксель у нас находится в координатах (dx+1, dy). Квадрат расстояния до него будет (dx+1)^2+dy^2 = dx*dx + 2*dx + 1 + dy*dy = (dx*dx + dy*dy) + 2*dx + 1
А поскольку (dx*dx + dy*dy) = старое расстояние Distace^2, то можно к нему просто прибавить 2*dx + 1, чтобы получить новую дистанцию.
Вот откуда взялось 2 * q.x + 1 и 2 * (q.x + q.y + 1)
А теперь суть. Данный подход выливается вот в такую реализацию:
static inline void Compare(Grid &g, Point &p, int x, int y, int offsetx, int offsety)
{
int add;
Point other = Get(g, x + offsetx, y + offsety);
if(offsety == 0) {
add = 2 * other.dx + 1;
}
else if(offsetx == 0) {
add = 2 * other.dy + 1;
}
else {
add = 2 * (other.dy + other.dx + 1);
}
other.f += add;
if (other.f < p.f)
{
p.f = other.f;
if(offsety == 0) {
p.dx = other.dx + 1;
p.dy = other.dy;
}
else if(offsetx == 0) {
p.dy = other.dy + 1;
p.dx = other.dx;
}
else {
p.dy = other.dy + 1;
p.dx = other.dx + 1;
}
}
}
Так как алгоритм писался в бородатые годы, то ради экономии операций тут куча ветвлений, и как результат — потенциальных ошибок branch prediction. Мне кажется гораздо быстрее будет подсчитать квадрат расстояния налету:
static inline void Compare(Grid &g, Point &p, int x, int y, int offsetx, int offsety)
{
Point newPoint;
Point other = Get(g, x + offsetx, y + offsety);
newPoint.dx = (other.dx + abs(offsetx));
newPoint.dy = (other.dy + abs(offsety));
newPoint.f = newPoint.dx*newPoint.dx + newPoint.dy*newPoint.dy;
if (newPoint.f < p.f)
{
p = newPoint;
}
}
А так же возможно будет быстрее вообще избавиться от хранения квадрата дистанции в изображении. Выкидываем поле f из структуры:
struct Point
{
short dx, dy;
};
а функцию Compare переписываем вот так:
static inline void Compare(Grid &g, Point &p, int x, int y, int offsetx, int offsety)
{
Point newPoint;
int newDist;
Point other = Get(g, x + offsetx, y + offsety);
newPoint.dx = (other.dx + abs(offsetx));
newPoint.dy = (other.dy + abs(offsety));
newDist = newPoint.dx*newPoint.dx + newPoint.dy*newPoint.dy;
if ( newDist < (p.dx*p.dx + p.dy*p.dy) )
{
p = newPoint;
}
}
Так как мы храним дельты по осям: dx и dy, а сравнивать нам нужно дистанцию (и записывать минимальную), то нам придется каждый раз вычислять квадрат расстояния dx*dx+dy*dy, чтобы мы могли его сравнить. Авторы решили сэкономить на этом.
Это на самом деле я и есть автор этого бреда. С математической точки зрения это выглядит как неоптимизированный код, но на самом деле эта функция написана специально под компилятор (ветвления выкидываются путём подстановки констант) — то есть в финальном скомпилированном варианте не будет практически ни единого ветвления. И доп. переменную с квадратом расстояния тоже делал я:) Поскольку мне надо было добиться скорости алгоритма менее 1 секунды для изображения 4к, получился вот такой монстр. Сделать лучше при той же производительности не получилось (этот код быстрее где-то на 15%).
Но комментарий не мешало бы оставить, так как с бородатых лет я уже сам не помню, что я тут натворил. Причем я потом нашёл такую же оптимизацию в китайской статье, которую приводил в ссылках, но там сам алгоритм неточный.
P.S. То что сейчас в гите — сильно устарело.
Я смотрел ссылку которую вы приводили в моем посте: www.ee.bgu.ac.il/~dinstein/stip2002/LeymarieLevineDistTrans_cvgip92.pdf
Вот эти 2 * (q.dx + q.dy + 1) и 2 * q.dx + 1 предполагают экономию в пару операций умножения и одно сложение, но при этом требуют хранить дистанцию. Копчиком чую, что на современном железе проще сделать пару умножений и сложений вместо лишней записи/чтения значения. Вам не сложно проверить на скорость вариант без f в Point, который я предложил выше?
Вот эти 2 * (q.dx + q.dy + 1) и 2 * q.dx + 1 предполагают экономию в пару операций умножения и одно сложение, но при этом требуют хранить дистанцию. Копчиком чую, что на современном железе проще сделать пару умножений и сложений вместо лишней записи/чтения значения. Вам не сложно проверить на скорость вариант без f в Point, который я предложил выше?
Эта ссылка — оригинальные методы 4SED и 8SED 1992 года. Я нашёл оптимизированный, но неправильный метод. Ещё полезно почитать статью где все алгоритмы собраны — там вроде бы всё правильно и присутствует сравнение, исходя из которого я сделал вывод что 8SED самый быстрый и ленивый из методов, дающих мизерную ошибку (с дейкстрой и графами уж точно не захочется заморачиваться).
Проверил, если не кэшировать дистанцию, время выполнения функции GenerateSDF увеличивается почти в 2 раза. И это я ещё не считаю того, что в конце нужно извлечь корень из дистанции, без кэша это ещё две допполнительные операции умножения. На 4к изображении разница уж очень велика: 0.22 сек против 0.4 сек (не считая копирования в Qt текстуру).
Вот текущий немного кривой код: gist.github.com/scriptum/e5a5961e71465bc67181
Проверил, если не кэшировать дистанцию, время выполнения функции GenerateSDF увеличивается почти в 2 раза. И это я ещё не считаю того, что в конце нужно извлечь корень из дистанции, без кэша это ещё две допполнительные операции умножения. На 4к изображении разница уж очень велика: 0.22 сек против 0.4 сек (не считая копирования в Qt текстуру).
Вот текущий немного кривой код: gist.github.com/scriptum/e5a5961e71465bc67181
Sign up to leave a comment.
Signed Distance Field или как сделать из растра вектор