Comments 96
Я понял, что если автор продолжит обучение математике и напишет статью о том, что 2х2=5, прочитав ее, я соглашусь.
Путём переопределения операции x этого добиться не так уж и сложно. По сути ведь математические операции это всего лишь отношения множеств. Но в этом случае выражение 2x2=5 будет обозначать совершенно не то, что мы обычно подразумеваем.
Но ведь уже есть «лазейка», доказывающая, что 2х2=5 :)
Вспомнился Перельман
Сейчас мы вместе с вами докажем, что дважды два равно пяти. Это можно сделать буквально на пальцах:
Имеем равенство:
16 — 36 = 25 — 45 (1)
Прибавим к левой и правой части 81/4:
16 — 36 + 81/4 = 25 — 45 + 81/4 (2)
Преобразуем выражение:
4*4 — 2*4*9/2 + (9/2)*(9/2) = 5*5 — 2*5*9/2 + (9/2)*(9/2) (3)
Теперь можно заметить, что в левой и правой части выражения (3) записаны произведения вида:
a2-2ab+b2, то есть, квадрат разности: (a-b)2. В нашем случае слева a=4, b=9/2, а справа a=5, b=9/2. Поэтому перепишем выражение (3) в виде квадратов разности:
(4 — 9/2)2 = (5 — 9/2)2 (4)
А следовательно,
4 — 9/2 = 5 — 9/2 (5)
И наконец, получаем долгожданное равенство:
4 = 5
или, если угодно,
2*2 = 5
Попробуйте объяснить, как это возможно, что дважды два равно пяти?
Имеем равенство:
16 — 36 = 25 — 45 (1)
Прибавим к левой и правой части 81/4:
16 — 36 + 81/4 = 25 — 45 + 81/4 (2)
Преобразуем выражение:
4*4 — 2*4*9/2 + (9/2)*(9/2) = 5*5 — 2*5*9/2 + (9/2)*(9/2) (3)
Теперь можно заметить, что в левой и правой части выражения (3) записаны произведения вида:
a2-2ab+b2, то есть, квадрат разности: (a-b)2. В нашем случае слева a=4, b=9/2, а справа a=5, b=9/2. Поэтому перепишем выражение (3) в виде квадратов разности:
(4 — 9/2)2 = (5 — 9/2)2 (4)
А следовательно,
4 — 9/2 = 5 — 9/2 (5)
И наконец, получаем долгожданное равенство:
4 = 5
или, если угодно,
2*2 = 5
Попробуйте объяснить, как это возможно, что дважды два равно пяти?
Разгадка
(4 – 9/2)2 = (5 – 9/2)2
А следовательно,
4 – 9/2 = 5 – 9/2
А следовательно,
4 – 9/2 = 5 – 9/2
Выражение (5) неверно и должно выглядеть так:
|4 — 9/2| = |5 — 9/2|
Соответственно из него уже не следует, что 4=5.
|4 — 9/2| = |5 — 9/2|
Соответственно из него уже не следует, что 4=5.
Всё просто: в равенстве (5) не хватает модуля :).
Как, как… Мы не можем просто так, без условий освободиться от квадратов (4).
Однако, вопрос о делении на ноль ни разу не относится к числу сложных вопросов, и для меня остается загадкой, почему с ним возникает столько проблем.
Думаю, такое объяснение для ребенка далеко не простое.
Однако, вопрос о делении на ноль ни разу не относится к числу сложных вопросов, и для меня остается загадкой, почему с ним возникает столько проблем.Я думаю, потому, что в курсе математического анализа для обозначения бесконечно малых величин используется символ ноля. И там же рассматривается вопрос деления на бесконечно малые, где повсеместно встречаются разнообразные «деления на ноль». К сожалению, при выходе из школы забывается, что там речь шла о бесконечно малых, в памяти отпечатывается только то, что в начальной школе учителя бесстыдно врали на уроках арифметики и на ноль делить всё же можно, ведь в десятом классе показывали! В качестве аргументов приводятся калькуляторы и IEEE 754.
Объяснить, почему на 0 делить нельзя математически очень просто. По тривиальности это доказательство расположено где-то недалеко от утверждений «все простые числа, кроме 2, нечётные» и бинома Ньютона.
Однако, очевидно, что сложность этого вопроса не в этом — это правило, в отличие от нечётности простых чисел, нам интуитивно кажется непонятным.
Кольцо рациональных чисел конструируется естественным образом:
— берём мощности множеств (натуральные числа)
— вводим операцию сложения
— вводим обратные по операции сложения числа (отрицательные)
— вводим операцию умножения
— вводим обратные по этой операции числа.
И тут — упс — пятый пункт выполнить нельзя, ноль мешает.
Причём, что характерно, с этим кольцом можно и дальше работать:
— вводим понятие предела последовательности
— проводим операцию пополнения, получаем множество действительных чисел
— вводим операцию возведения в степень
— доопределяем всюду эту операцию, получаем множество комплексных чисел
А ноль так и болтается. Когнитивный диссонанс.
А теперь совсем немножко философии: если посмотреть на все эти конструкции, то очевидно, что все они строятся по принципу «а теперь давайте попробуем придумать операцию x». Придумали? Вроде получилось, ничего. Невозможность делить на ноль — это следствие нашей неспособности так вообразить себе числа, чтобы на ноль делить было можно. Это и раздражает.
Однако, очевидно, что сложность этого вопроса не в этом — это правило, в отличие от нечётности простых чисел, нам интуитивно кажется непонятным.
Кольцо рациональных чисел конструируется естественным образом:
— берём мощности множеств (натуральные числа)
— вводим операцию сложения
— вводим обратные по операции сложения числа (отрицательные)
— вводим операцию умножения
— вводим обратные по этой операции числа.
И тут — упс — пятый пункт выполнить нельзя, ноль мешает.
Причём, что характерно, с этим кольцом можно и дальше работать:
— вводим понятие предела последовательности
— проводим операцию пополнения, получаем множество действительных чисел
— вводим операцию возведения в степень
— доопределяем всюду эту операцию, получаем множество комплексных чисел
А ноль так и болтается. Когнитивный диссонанс.
А теперь совсем немножко философии: если посмотреть на все эти конструкции, то очевидно, что все они строятся по принципу «а теперь давайте попробуем придумать операцию x». Придумали? Вроде получилось, ничего. Невозможность делить на ноль — это следствие нашей неспособности так вообразить себе числа, чтобы на ноль делить было можно. Это и раздражает.
Я понял, что мой интеллект не достаточен для понимания этого простого объяснения.
Когда я объяснял своему сыну-первокласснику почему нельзя делить на ноль, я действовал так:
Я: У нас есть 4 яблока и 4 мальчика. Надо раздать им имеющиеся яблоки поровну. Сколько яблок будет у каждого мальчика?
Он: 1
Я: У нас есть 4 яблока и 2 мальчика. Надо раздать им имеющиеся яблоки поровну. Сколько яблок будет у каждого мальчика?
Он: 2
Я: Хорошо, теперь у нас есть опять 4 яблока, надо раздать их 1 мальчику. Сколько у него будет яблок?
Он: 4
Я: А теперь, если у нас есть 4 яблока, но мы решили их никому не раздавать, сколько у этого «никого» будет яблок?
Он: Не знаю.
Я: Именно, вопрос о том, сколько яблок будет у «никого» (==0) некорректен при такой постановке задачи. Т.е. посчитать это невозможно в принципе.
Когда я объяснял своему сыну-первокласснику почему нельзя делить на ноль, я действовал так:
Я: У нас есть 4 яблока и 4 мальчика. Надо раздать им имеющиеся яблоки поровну. Сколько яблок будет у каждого мальчика?
Он: 1
Я: У нас есть 4 яблока и 2 мальчика. Надо раздать им имеющиеся яблоки поровну. Сколько яблок будет у каждого мальчика?
Он: 2
Я: Хорошо, теперь у нас есть опять 4 яблока, надо раздать их 1 мальчику. Сколько у него будет яблок?
Он: 4
Я: А теперь, если у нас есть 4 яблока, но мы решили их никому не раздавать, сколько у этого «никого» будет яблок?
Он: Не знаю.
Я: Именно, вопрос о том, сколько яблок будет у «никого» (==0) некорректен при такой постановке задачи. Т.е. посчитать это невозможно в принципе.
На это можно по-детски возразить: «у Никого будет 0 яблок, так как мы все их оставили у себя». Но это неверно. Верно: частное не определено, так как оно результат выполнения алгоритма деления, а его выполнить невозможно, никому не отдавая яблоки. Я об этом писал в своей заметке, описывая вычисления с фасолью.
Если мы определили сущность «Никто» значит можно задать ей и свойство «возможность иметь яблоки». А так как яблок у этой сущности нет (они все у нас) — значит у нее 0 яблок. Т.е., задавая вопрос именно в такой постановке (используя местоимения, одушевляя слово «Никто») — получить ответ можно.
Это зависит от того, инициализируется ли свойство нулем или нет. Если нет — то там «мусор», то самое " не знаю". ;-)
Если мы уже перешли в программирование, то свойство будет инициализировано в момент создания объекта, а так как тип у него будет число, то инициализировано нулем. А объем мы создаем — так как уже обращаемся к нему за значением этого свойства.
Если же говорить без программирования, то вот аллегория: «Никто надел на руки перчатки. Вопрос: каково минимальное число рук у никто?».
Если же говорить без программирования, то вот аллегория: «Никто надел на руки перчатки. Вопрос: каково минимальное число рук у никто?».
А максимальное нас не интересует, важен факт словесного определения сущности.
Ноль гекатонхейров это ноль, а 1 никто — это 1. Поэтому 0*кол-во рук у гекатонхейра = 0, а 1 * мин1рука = 1
Ноль гекатонхейров это ноль, а 1 никто — это 1. Поэтому 0*кол-во рук у гекатонхейра = 0, а 1 * мин1рука = 1
Если начать разбираться взрослому человеку, то наверное к подобному определению можно придти. Напомню, что речь шла о попытке объяснить ребенку невозможность деления на ноль путем введения неопределенности. Однако формулировка вопроса не подразумевает неопределенности. Есть какой-то «никто» и у него есть сколько-то яблок.
свойство будет инициализировано в момент создания объекта, а так как тип у него будет число, то инициализировано нулем.Будет ли там сущность, а будет ли момент создания… Ладно, допустим, будет. Кто вам сказал, что числа инициализируются нулем? Даже если не говорить о моем собственном языке, где я могу инициализировать рандомом, в С++ (к примеру) примитивные типы-данные инициализируются тем, что было на в этом месте памяти до создания объекта (то есть мусором).
В С++ это просто эволюционная недоработка методологии (какой смысл в свойстве объекта неизвестно какого типа?), а если мы сами инициализируем рандомом, то мы об этом знаем, а значит начальные условия и задача меняются:
«Есть никто у которого по умолчанию число яблок = random. Мы не дали ему ничего, сколько у него яблок».
«Есть никто у которого по умолчанию число яблок = random. Мы не дали ему ничего, сколько у него яблок».
Неизвестно какого типа? Wtf?Примитивные типы. Я вам говорю, что если у вас есть какой-то неведомый никто, то чем там у него что инициализируется — неизвестно. Может, нулем, может единицей, а потрогать — нельзя. А вы мне — там нуль и всё. А рандомом инициализируем не мы, а создатель «компилятора», посыл тот же — мы не знаем, сколько яблок было у никого.
Не важно, кто инициализирует, важно что мы знаем об этом.
По поводу типов — тип нужен для того, чтобы заявить об интерфейсе и затем совершать с ним вполне определенные операции. Если мы не уверены в содержимом свойства уже созданного нами объекта (а вдруг там мусор), то смысла в таком типизированном свойстве нет. Если тип int, а на деле там строка, то каким образом мы, зная об интерфейсе объекта, должны, например, складывать другое целое число со свойством?
По поводу типов — тип нужен для того, чтобы заявить об интерфейсе и затем совершать с ним вполне определенные операции. Если мы не уверены в содержимом свойства уже созданного нами объекта (а вдруг там мусор), то смысла в таком типизированном свойстве нет. Если тип int, а на деле там строка, то каким образом мы, зная об интерфейсе объекта, должны, например, складывать другое целое число со свойством?
Если мы не уверены в содержимом свойства уже созданного нами объекта (а вдруг там мусор), то смысла в таком типизированном свойстве нет.
Смысла нет, если после создания объекта первое, что мы собираемся делать — это читать значение объекта. Но кто сказал, что первым действием является обязательно чтение? Запись — это тоже операция, заданная интерфейсом типа (если это не read-only объект, который обязан быть консистентным для чтения с момента создания). Собственно, запись всегда идёт первой после создания, просто в других языках она накрепко прибита к созданию и называется «инициализация значением по-умолчанию». С++ позволяет делать инициализацию в другом месте, не платя за «бесплатную» обязательную дефолтную инициализацию — но отсуствие принудительных дефолтов вовсе не нарушает интерфейс и систему типов. Неинициализированный int всё-равно содержит int-овое значение (хоть и произвольное), а не строку или структуру; и он полностью поддерживает интерфейс всех int-овых операций — можно складывать и умножать и результат будет детерминирован тем значением, что там оказалось.
Смысла нет, если после создания объекта первое, что мы собираемся делать — это читать значение объекта. Но кто сказал, что первым действием является обязательно чтение? Запись — это тоже операция, заданная интерфейсом типа (если это не read-only объект, который обязан быть консистентным для чтения с момента создания). Собственно, запись всегда идёт первой после создания, просто в других языках она накрепко прибита к созданию и называется «инициализация значением по-умолчанию». С++ позволяет делать инициализацию в другом месте, не платя за «бесплатную» обязательную дефолтную инициализацию — но отсуствие принудительных дефолтов вовсе не нарушает интерфейс и систему типов. Неинициализированный int всё-равно содержит int-овое значение (хоть и произвольное), а не строку или структуру; и он полностью поддерживает интерфейс всех int-овых операций — можно складывать и умножать и результат будет детерминирован тем значением, что там оказалось.
Ну и да, ноль — это не всегда правильное дефолтное значение. Вполне можно вообразить ситуации, где правильный дефолт — единица. Скажем, для инициализации сомножителей единица явно лучше, так как она не меняет результат умножения. Или взять матрицы — должна ли матрица быть инициализирована нулями, или это должна быть identity matrix (диагональ инициализирована единицами, остальное — нулями)?
Т.е. видно, что вырисовывается некое правило: хороший дефолт — это identity element. Но для разных операций он разный — для сложения нуль, для умножения единица и т.д.
Т.е. видно, что вырисовывается некое правило: хороший дефолт — это identity element. Но для разных операций он разный — для сложения нуль, для умножения единица и т.д.
Возможно я не совсем ясно передал суть объяснения.
Я не пытался в объяснении ввести сущность «никто». Я пытался объяснить ему, что т.к. отдавать яблоки было некому, то и само понятие о том, сколько яблок у «этого некто» в принципе не имеет смысла.
Я не пытался в объяснении ввести сущность «никто». Я пытался объяснить ему, что т.к. отдавать яблоки было некому, то и само понятие о том, сколько яблок у «этого некто» в принципе не имеет смысла.
Я: А теперь, если у нас есть 4 яблока, но мы решили их никому не раздавать, сколько у этого «никого» будет яблок?
Он: Не знаю.
Я: Именно, вопрос о том, сколько яблок будет у «никого» (==0) некорректен при такой постановке задачи. Т.е. посчитать это невозможно в принципе.
Я: А теперь, если у нас есть 4 яблока, но мы решили их дать минус одному человеку, сколько у этого античеловека будет яблок?
Он: Не знаю.
Кстати, к бобовому калькулятору из статьи это тоже относится.
«Естественный» смысл отрицательных чисел — учет долгов… Это не такая простая и совсем не очевидная тема. А деления на отрицательные числа можно избежать, используя правило знаков.
На бобовом калькуляторе для вычислений в целых числах нужно использовать фасоль двух цветов — красную и белую.
На бобовом калькуляторе для вычислений в целых числах нужно использовать фасоль двух цветов — красную и белую.
Подобные методы математически верны, а вот физический смысл меняется. «Дали четыре яблока минус одному человеку» физического смысла не имело, «один человек вернул четыре яблока» — смысл появился.
И это — не говоря уже о неполиткорректной дискриминации фасоли по цветовому признаку.
И это — не говоря уже о неполиткорректной дискриминации фасоли по цветовому признаку.
Имхо, лучше вместо долгов использовать, скажем, высоты выше/ниже уровня моря. Тогда в дальнейшем будет легче объяснить, что нулевая отметка — это зачастую просто условность, которую можно смещать по ситуации.
К сожалению, с таким подходом трудно объяснить умножение и деление. Там от сдвига нулевой отметки результат будет меняться…
Про относительность нуля — это позже рассказывать, не смешивая с умножением.
Умножение длин — это просто площади прямоугольников, его ещё на натуральных числах (рядах кубиков) объясняют. На целые/вещественные числа распространяется легко по аналогии. Единственное новое — знаки.
Знаки площадей можно демонстрировать, штрихуя полуплоскости (скажем, положительные — правой штриховкой, отрицательные — левой штриховкой) и постулируя, что «отрицательная» площадь — это та, которая оказалась заштрихованной крест-накрест. Для наглядности заменить штриховку поляризатором (заодно рассказать/показать про поляризацию света) или, скажем, решёткой в тюремной камере: «пропускает свет/можно разогнуть и сбежать» — это «положительная площадь», «задерживает свет/нельзя разогнуть и убежать» — «отрицательная площадь».
Умножение длин — это просто площади прямоугольников, его ещё на натуральных числах (рядах кубиков) объясняют. На целые/вещественные числа распространяется легко по аналогии. Единственное новое — знаки.
Знаки площадей можно демонстрировать, штрихуя полуплоскости (скажем, положительные — правой штриховкой, отрицательные — левой штриховкой) и постулируя, что «отрицательная» площадь — это та, которая оказалась заштрихованной крест-накрест. Для наглядности заменить штриховку поляризатором (заодно рассказать/показать про поляризацию света) или, скажем, решёткой в тюремной камере: «пропускает свет/можно разогнуть и сбежать» — это «положительная площадь», «задерживает свет/нельзя разогнуть и убежать» — «отрицательная площадь».
Согласен.
Открывал статью в надежде — Ну вот тут, то наверно и правда по простому объяснят. А нет, и тут обманочка.
Открывал статью в надежде — Ну вот тут, то наверно и правда по простому объяснят. А нет, и тут обманочка.
По-моему, непонимание возникает только если понимать «нельзя» как «запрещают», а не как «результат не определён». Во втором случае «на ноль делить нельзя» по тем же причинам, по которым нельзя к числу прибавить треугольник, например.
Когда я учился во втором классе (боже, как давно это было), в нашем учебнике было вполне понятное объяснение. Дословно не воспроизведу, но по смыслу примерно такое (разумеется, в оригинале оно было без буквенных обозначений, во втором классе-то): «Что значит поделить число A на число B? Это значит, найти число С, которое после умножения на B будет равно A. Если B равно нулю, то каким бы ни было число C, всё равно при умножении будет получаться ноль, а на A. Вывод — делить на ноль нельзя». В своё время меня в мои 8 лет это объяснение полностью удовлетворило.
Хорошая статья. Видно, что математик писал.
Когда я в свое время пристал к маме с этим вопросом, она дала мне калькулятор, велела вычислить 1 / 1, 1 / 0.1, 1 / 0.01, 1 / 0.001 и так далее. Когда у калькулятора кончились разряды, она сказала, что получится число, больше любого другого, поэтому результат нельзя записать. Меня это удовлетворило.
Мама по образованию журналист :)
Мама по образованию журналист :)
Вот, слово «нельзя» прям коробит. «Нельзя» мочить манту. Можно ли сказать, что это действие бессмысленно в каком-то определенном описании Вселенной. И где деление на ноль очень пригодилось бы? Думается вопрос «зачем» делить звучит лучше.
Точка как знак умножения ужасно. Так и хочется прочитать как 1, х вместо 1*х.
Хочу напомнить, что на уроках математики иначе как точкой умножение никогда и не записывали.
А в ПК иначе как * никто не пишет. Для бумаги точка удобно не спутаешь с х например. Но для отображения на мониторах очень плохо писать точку.
А на форуме dxdy.ru за * в формулах наказывают:) Но согласен с критикой — в этой статье точка читается не очень хорошо.
К сожалению, я пока не научился использовать tex на Хабре, а MathJax, который я использую в своем блоге — с ним формулы читабельнее — здесь вроде бы не поддерживается…
В будущих статьях учту ваши замечания.
К сожалению, я пока не научился использовать tex на Хабре, а MathJax, который я использую в своем блоге — с ним формулы читабельнее — здесь вроде бы не поддерживается…
В будущих статьях учту ваши замечания.
Коллеги. Позвольте высказать мнение, что хоть математика и абстрактная наука, но всё-таки некоторые вещи должны быть учтены в контексте. Ещё со школы меня учили, что делят не на число, а на части. Не бывает в конкретном предмете нуля частей. Конкретный предмет может быть только целым.
Однако надо помнить, что есть предметы, а есть вещества/материалы. Предмет нельзя разделить на части, потому что часть уже будет не предметом. Если яблоко разделить на две части, то каждая из частей уже не будет яблоком. Если табуретку разделить на две части, то каждая из частей не будет табуреткой. Можно разделить песок на части, потому что каждая из частей будет песком. Но всё равно — делят на части, а не на число. Можно разделить какое-то свойство предмета на части. Тот же килограмм яблок можно разделить на две части. После деления не должно появляться другой размерности в конечном результате.
Однако надо помнить, что есть предметы, а есть вещества/материалы. Предмет нельзя разделить на части, потому что часть уже будет не предметом. Если яблоко разделить на две части, то каждая из частей уже не будет яблоком. Если табуретку разделить на две части, то каждая из частей не будет табуреткой. Можно разделить песок на части, потому что каждая из частей будет песком. Но всё равно — делят на части, а не на число. Можно разделить какое-то свойство предмета на части. Тот же килограмм яблок можно разделить на две части. После деления не должно появляться другой размерности в конечном результате.
Сначала найдите среднюю скорость пешехода (школьная задача из области физики), а потом уже рассуждайте и том, что
делят не на число, а на части
После деления не должно появляться другой размерности в конечном результате.
Детские вопросы обычно очень сложны
Я предложил ответ на «детский» вопрос.
Нельзя преподавать математику таким образом, чтобы действия, запрещенные вчера, сегодня разрешались.
Но ведь ровно так преподают математику везде. И ровно так она развивалась исторически. Начиная с «корней из минус единицы» и «деления на рациональные и иррациональные числа» и заканчивая теорией полей-колец-групп, где умножают и делят что попало на что попало.
И я никогда не видел с этим педагогической проблемы. Нельзя вываливать на ученика слишком много информации сразу.
И я никогда не видел с этим педагогической проблемы. Нельзя вываливать на ученика слишком много информации сразу.
А никто не говорит, что надо вываливать все сразу. Но нельзя запрещать выполнять правильные с точки зрения математики действия. А то получается какое-то математическое лицемерие — «правильный ответ такой-то, но мы этого еще не проходили, поэтому напишем что нет решений»…
Я так понимаю, исходя из Вашей формулировки иррациональные числа нужно срочно запретить?
Хороший комментарий. Арабский ученый XII века, о котором я писал в своей заметке, видимо, рассуждал аналогичным образом, когда предлагал менять яйца на соль.
Но мы-то уже знаем, что числа делятся на части которые суть числа.
Но мы-то уже знаем, что числа делятся на части которые суть числа.
Если яблоко разделить на две части, то каждая из частей уже не будет яблоком. Если табуретку разделить на две части, то каждая из частей не будет табуреткой. Можно разделить песок на части, потому что каждая из частей будет песком. Но всё равно — делят на части, а не на число. Можно разделить какое-то свойство предмета на части.
…
Что, простите?
Здесь почти всё логично. Неделимый предмет, разделённый на части, утрачивает свой смысл. С яблоком не так очевидно, яблоко ещё можно съесть или вынуть косточки и посадить. Более яркий пример — микропроцессор. Купили себе один помощнее, а с другом поделиться хочется. Отпиливаете ровно половину, отдаёте ему…
С песком, пока мы не дошли до долей грамма, всё наоборот. Делим его, а не ломается.
«Но всё равно — делят на части, а не на число.» — спорное утверждение в общем смысле, но в рамках дробления физических объектов вполне уместное.
С песком, пока мы не дошли до долей грамма, всё наоборот. Делим его, а не ломается.
«Но всё равно — делят на части, а не на число.» — спорное утверждение в общем смысле, но в рамках дробления физических объектов вполне уместное.
Эта грустная история о прекрасной восточной девушке Наноль, которая любит двух прекрасных и мужественных юношей и не может выбрать.
Юноши тоже любят ее. Казалось бы, просто в нынешние–то времена, зажить бы им простой и дружной семьей.
Но трагедия в том, что Наноль делить нельзя.
Юноши тоже любят ее. Казалось бы, просто в нынешние–то времена, зажить бы им простой и дружной семьей.
Но трагедия в том, что Наноль делить нельзя.
Западная, думаете, с дележкой не морочилась бы сильно?
В расширенной комплексной плоскости делить на ноль можно. Точки 0 и бесконечность ничем не выделяются из остальных. Правда это уже не поле.
Простите, но что именно не верно? Есть такое обобщение, и в его рамках делить на 0 можно.
Точно так же, в школе функция это однозначное отображение одного множества на другое, в ТФКП функциями называются обобщенные функции, допускающие многозначность. А ноль и бесконечность являются не более чем точками, бесконечность называется несобственным комплексным числом. Вычет в бесконечности по своей сути ничем не отличается от вычета в нуле и любой другой точке. Договорились, что a/∞ = 0, ∞/a = ∞, a/0 = ∞; 0/0, ∞/∞, 0*∞, ∞±∞объявлены лишенными смысла.
Точно так же, в школе функция это однозначное отображение одного множества на другое, в ТФКП функциями называются обобщенные функции, допускающие многозначность. А ноль и бесконечность являются не более чем точками, бесконечность называется несобственным комплексным числом. Вычет в бесконечности по своей сути ничем не отличается от вычета в нуле и любой другой точке. Договорились, что a/∞ = 0, ∞/a = ∞, a/0 = ∞; 0/0, ∞/∞, 0*∞, ∞±∞объявлены лишенными смысла.
А в записи «a/0 = ∞», в каком именно смысле символ "/" — это деление?
Автор уже упоминал это обобщение в статье, сколько раз можно упоминать его в комментариях?
1) в статье упоминаний нет, упомянута ссылка Wheel theory(к тому же англоязычная), что для подавляющей части аудитории ничего не говорит.
2) ни одного упоминания «ТФКП» на данной странице, есть упоминание «комплексные числа», но в несколько другом, размытом контектсте
3) _возможность_ деления на ноль в не экзотических разделах математики довольно существенна, по моему скромному мнению
2) ни одного упоминания «ТФКП» на данной странице, есть упоминание «комплексные числа», но в несколько другом, размытом контектсте
3) _возможность_ деления на ноль в не экзотических разделах математики довольно существенна, по моему скромному мнению
Почему же мы не можем сказать, что 1/x=∞ — есть некоторое число?
Мне кажется, здесь и кроется подхвох. Кто сказал, что «1/0=∞»?
Это, примерно, как при переходе a^2 = b^2 => a = b, забыть про модуль.
Так можно и к 4=5 прийти.
Мы сами придумали «1/0=∞», исходя из интуиции, а теперь пытаемся подвести решение под ответ.
По идее, 1/x и 2/x — разные числа. Так же разными должны быть 1/0 и 2/0.
Естественно, если мы посчитаем «1/0 = ∞» и «2/0 = ∞», то здесь мы «с водой выбросили ребенка», т.е. теряем делимое, и приходим к 1=0, 1=2 и т.д.
Как дилетантское решение, мы можем выдумать число «анти ноль» (ну или «гипер ноль», чтобы попонтовее), равное 1/0.
Обозначим его, как "^0^" (такая летучая мышко :) ).
И проблема решается:
x/0 = x * ^0^.
И тогда x/0 и y/0 останутся разными числами.
Правда это уже будет из области комплексных чисел, но никаких несостыковок (типа 0=1) уже не будет.
Будет. Операция умножения потеряет свойства ассоциативности и дистрибутивности относительно сложения-вычитания.
Да, согласен, дилетантское решение не подходит.
Но прошу обратить внимание на первую часть комментария.
Кто сказал, что «1/0=∞»?
Но прошу обратить внимание на первую часть комментария.
Кто сказал, что «1/0=∞»?
Если не нравится знак бесконечности, обозначьте это число как-либо еще. Например, omega. Дальнейшее рассуждение, приводящее к равенству всех чисел, не изменится.
Изменится:
1/0 = omega
2/0 = 2*omega
Суть в приравнении 1/0 = 2/0.
Из этого маленького упущения вы в статье и приходите к вопросу «Ну разве это не полная чушь?».
1/0 = omega
2/0 = 2*omega
Суть в приравнении 1/0 = 2/0.
Из этого маленького упущения вы в статье и приходите к вопросу «Ну разве это не полная чушь?».
Да нет же, я исхожу из следующих посылок:
1). Для любого x верно 1*x = x;
2) Для любого x верно x — x = 0;
3) omega есть такое число, что имеет место равенство 0 * omega = 1;
4) Правила 1) и 2) верны и для omega.
1). Для любого x верно 1*x = x;
2) Для любого x верно x — x = 0;
3) omega есть такое число, что имеет место равенство 0 * omega = 1;
4) Правила 1) и 2) верны и для omega.
Ок, тогда чуши нет.
0 * omega = 1
0 * 2 omega = 2 (вместо предполагаемого 0 * omega = 2).
0 * omega = 1
0 * 2 omega = 2 (вместо предполагаемого 0 * omega = 2).
Вы, наверное, имеете в виду
1/0 = omega
2/0 = alpha
Иначе, если «2 omega» — это «2 * omega», как в вашем первом примере, то
0 * omega = 1
(0 * 2) * omega = 2
=>
0 * omega = 1
0 * omega = 2
что возвращает нас к равенству всех чисел.
А если с alpha, то
Однако, сейчас ноль определяется именно из операций, возможных с ним и, ИМХО, глупо было бы использовать то же обозначение для сущности с абсолютно другими свойствами.
1/0 = omega
2/0 = alpha
Иначе, если «2 omega» — это «2 * omega», как в вашем первом примере, то
0 * omega = 1
(0 * 2) * omega = 2
=>
0 * omega = 1
0 * omega = 2
что возвращает нас к равенству всех чисел.
А если с alpha, то
Вторая: отказаться от некоторых привычных правил умножения. В частности, от аксиомы 0⋅x=0. Говорят, что это возможно (см. en.wikipedia.org/wiki/Wheel_theory). Разумеется, этот вариант гораздо интереснее первого, но и он представляет собой такое изменение правил игры, которое сразу выводит нас за рамки классической арифметики.
Однако, сейчас ноль определяется именно из операций, возможных с ним и, ИМХО, глупо было бы использовать то же обозначение для сущности с абсолютно другими свойствами.
Простите, но вы читать умеете? Могу повторить еще раз, если вы сами не можете произвести замену
j на ^0^(2*0) * ^0^ = 0 * ^0^ = 12 * (0*^0^) = 2 * 1 = 2Первая часть комментария — это вопрос «Кто сказал, что «1/0=∞»?»
Здесь мы ставим равенство, которое нужно сначала доказать.
Здесь мы ставим равенство, которое нужно сначала доказать.
Его не надо доказывать, оно равно по определению:
Я пользовался исключительно вашим же определением.
мы можем выдумать число «анти ноль» (ну или «гипер ноль», чтобы попонтовее), равное 1/0.
Обозначим его, как "^0^" (такая летучая мышко :)
И проблема решается:
x/0 = x * ^0^.
Я пользовался исключительно вашим же определением.
Это я понял.
Вы меня убедили, что концепция «анти ноль» сходу не подходит.
Поэтому про неё можно забыть.
Мой вопрос нужно трактовать буквально: как у вас получилось, что x/0 равно бесконечности?
В википедии операция a/0=∞ встречается только в проективной геометрии.
Вы меня убедили, что концепция «анти ноль» сходу не подходит.
Поэтому про неё можно забыть.
Мой вопрос нужно трактовать буквально: как у вас получилось, что x/0 равно бесконечности?
В википедии операция a/0=∞ встречается только в проективной геометрии.
Почему нельзя делить на ноль, даже если очень хочется?
Потому что поле действительных чисел перестанет быть даже кольцом и весь матан нужно будет переделывать сначала, если вообще получится переделать во что-то вменяемое?
По-моему у вас пробел в доказательстве:
А с чего это?
Ранее вы полагаете: 1/0 = :inf: есть некоторое число.
Правило звучит: 0⋅a = 0 не так ли?
0⋅a=0, а с другой стороны поскольку 0=1−1 должно быть выполнено 0⋅a=1⋅a−1⋅a=0 Таким образом, имеем 0=0
В частности, с одной стороны должно быть верно соотношение 0⋅∞=1, а с другой стороны поскольку 0=1−1 должно быть выполнено 0⋅∞=1⋅∞−1⋅∞=0. Таким образом, имеем 1=0,
А с чего это?
0⋅∞=1
Ранее вы полагаете: 1/0 = :inf: есть некоторое число.
Правило звучит: 0⋅a = 0 не так ли?
0⋅a=0, а с другой стороны поскольку 0=1−1 должно быть выполнено 0⋅a=1⋅a−1⋅a=0 Таким образом, имеем 0=0
Если бы мне сказали, что «на ноль делить бесполезно» вместо «на ноль делить нельзя», я бы в своё время это понял быстрее.
Это было бы интуитивней и, даже скажу, логичней.
А так пришлось положиться на авторитет ЕГГОГ и создать исключительную дырку в логике моего мира.
Позже, разобрался, конечно, когда увидел гиперболу.
Впрочем, такая обманка меня не оскорбила. Как и «капуста-журавль».
Это было бы интуитивней и, даже скажу, логичней.
А так пришлось положиться на авторитет ЕГГОГ и создать исключительную дырку в логике моего мира.
Позже, разобрался, конечно, когда увидел гиперболу.
Впрочем, такая обманка меня не оскорбила. Как и «капуста-журавль».
Sign up to leave a comment.
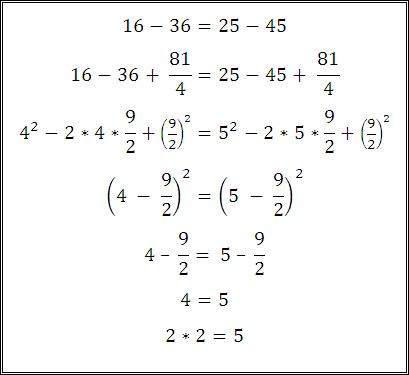

Почему нельзя делить на ноль, даже если очень хочется?