Часть 1.
Здравствуйте.
В этой статье я продолжу рассказ о том, как мы пишем под FireMonkey. Будет добавлено 2 интересных объекта. Оба напомнят нам о векторной алгебре и тригонометрии. Также в посте будут показаны приемы из ООП, которыми мы пользуемся.
Ряд линий (отличаются только пунктиром, точка-тире, точка-точка, etc), которые мы добавили, были сделаны по аналогии с описанием предыдущих примитивов. Теперь время перейти к более сложным фигурам (включая составные).
Первый примитив, который мы добавим, будет линия со стрелкой (стрелкой будет рисоваться обычный треугольник, но меньших размеров).
Для начала введем треугольник который «смотрит вправо». Для этого унаследуем обычный треугольник и перепишем ему метод Polygon, который отвечает за координаты вершин.
Вот так выглядят наши треугольники:

Далее унаследуем так называемый «маленький треугольник»:
Как видим, всё что мы сделали, это переопределили функции уникальные для нового треугольника.
Следующим классом добавим линию со стрелкой, которую унаследуем от обычной линии. В классе будет переопределена только процедура рисования самого примитива, то есть линию будет рисовать базовый класс, а вот треугольник — наследник.
Разбирать тут особо нечего, всё уже указано в комментариях, однако желающим вспомнить, что такое векторная алгебра и каким образом происходит работа с векторной графикой(перемещение, поворот различных фигур и т.д.), рекомендую замечательный пост на Хабре на эту тему, а также статьи «Векторы для чайников. Действия с векторами. Координаты вектора. Простейшие задачи с векторами» и «Линейная зависимость и линейная независимость векторов. Базис векторов. Аффинная система координат».
Как видим по рисунку, наш треугольник на данный момент рисуется только тогда, когда мы рисуем линию слева-направо:

Далее задача становится более интересной. Нам необходимо поворачивать треугольник, прямо перпендикулярно линии, которая его нарисовала. Для этого введем метод GetArrowAngleRotation, который будет рассчитывать угол поворота.
Для этого представим, что наша линия — это гипотенуза прямоугольного треугольника; далее найдем угол с катетом, который и будет углом поворота треугольника относительно линии:

Теперь наша линия выглядит так:
Следующий объект который мы добавим будет отвечать за перемещение фигур.
Алгоритм, которым мы воспользуемся:
1. Нам необходим метод для определения попадания точки в конкретную фигуру, скажем ContainsPt, для каждой фигуры; так как формулы для расчета попадания для каждой фигуры уникальны, пользуемся виртуальными функциями.
2. Следующий метод нам необходим для определения, в какую фигуру мы попали, если они пересекаются. Так как фигуры попадают в список по мере их появления на форме, то для случая пересечения фигур та из фигур, которая находится в начале списка, является последней появившейся, соответственно лежит «сверху». На самом деле, в этой логике есть прокол, однако по��а решим, что это правильно, а исправления оставим для следующего поста.
3. При первом нажатии в фигуру, в которую попали, мы должны изменить её контур или ряд других характеристик.
4. При втором нажатии мы должны переместить фигуру, в которую попали.
Сам класс перемещения будет наследоваться от стандартной фигуры, однако будет в себе хранить фигуру, которую он перемещает, и именно он при втором клике (в прошлом посте я описывал, в чём особенность рисования линий) будет перерисовывать фигуру.
Реализуем методы, которые я описал.
1. Метод определяет, попадает ли точка в фигуру(в нашем случае прямоугольник):
2. Этот метод при нажатии отвечает, нам на вопрос — в какую фигуру мы попали:
3. При первом нажатии в фигуру, в которую попали, мы должны изменить её контур или ряд других характеристик.
Для реализации следующего метода сделаем небольшой рефакторинг. Введем так называемый «контекст рисования»:
Если мы укажем фигуре в контексте рисования что она «перемещаемая», то рисование будет происходить иначе.
4. При втором нажатии мы должны переместить фигуру, в которую попали.
Для начала введём фабричный метод который отвечает за построение фигуры(список фигур необходим нам для того, что бы TmsMover смог обратиться ко всем фигурам, которые нарисованы в рамках текущей диаграммы).
Благодаря использованию классовой функции, мы принципиально разделили создание объекта перемещения и всех остальных фигур. Тем не менее, у этого подхода есть и отрицательная сторона. Например, мы ввели параметр создания aListWithOtherShapes, который совсем не нужен другим фигурам.
В контролере нам необходимо только изменить методы создания фигур:
Вызов CurrentAddedShape.EndTo(aFinish) в случае с мувером вызовет MoveTo, то есть переместит фигуру; перерисовку же, как видно выше, инициирует контролер:
Так как контролер отвечает за логику поведение фигур, то вынесем метод проверки «попадания в фигуру» в контролер, а при создании объектов будем передовать функцию проверки:
Так как для создания объектов необходимо передать 2 параметра, создаем контекст «создания»:
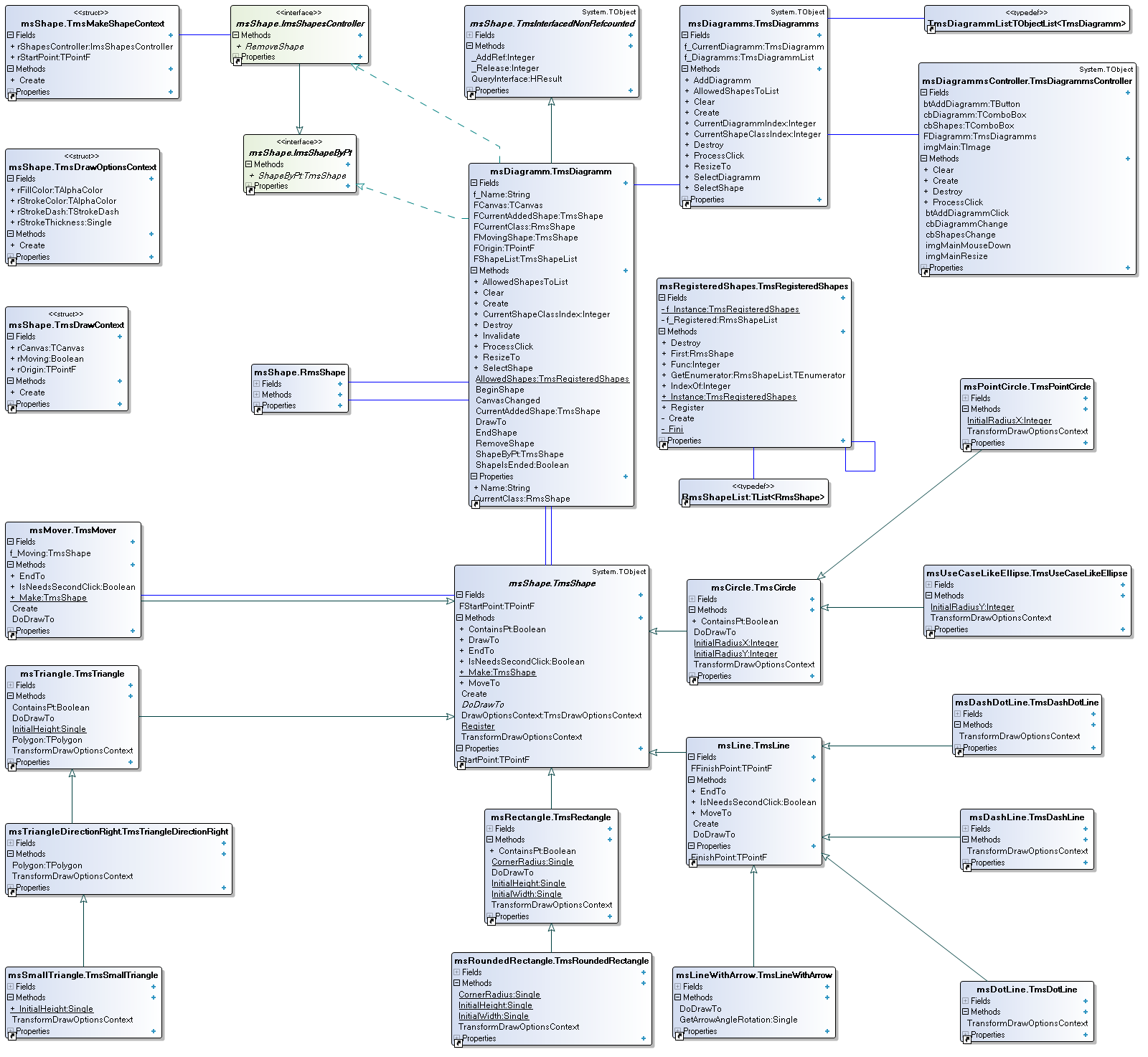
Добавим интерфейсы, которые будет реализовывать контролер, а также добавим класс интерфейсного объекта. В будущем в нём мы реализуем собственный подсчет ссылок.
Слегка изменим TmsMakeShapeContext:
Детальнее об интерфейсах и особенностях работы с ними в Delphi рекомендую 2 интерестных поста:
18delphi.blogspot.com/2013/04/iunknown.html
habrahabr.ru/post/181107
Сделаем наш контролер(TmsDiagramm) унаследованным от TmsInterfacedNonRefcounted и интерфейсов и изменим в методе BeginShape одну строчку.
было:
стало:
В случае с перемещением, метод EndTo который вызывается у мувера, примет такой вид:
В прошлом посте я рассказывал о том, как мы спрятали «уникальные настройки» (цвет заливки, толщина линий и т.д.) в виртуальные методы, которые каждая фигура устанавливает самостоятельно. Например:
Все настройки фигур «упаковываем» в контекст:
В классе TmsShape делаем виртуальную процедуру по аналогии с предыдущим пример. В будущем мы с легкостью расширим количество настроек уникальных для фигуры:
Благодаря контексту, убираем логику (мувер ли мы рисуем ?) из метода рисования и прячем её в конструктор записи:
После чего наш метод для рисования будут выглядеть так:
Всё, что нам осталось для того, чтобы наши объекты перемещались, это написать каждой фигуре метод ContainsPt, который будет проверять, попала ли точка в фигуру. Обычная тригонометрия, все формулы есть на просторах интернета.
Слегка переделаем регистрацию объектов в контейнере. Сейчас каждый класс «регистрирует» сам себя. Вынесем регистрацию в отдельный модуль.
В контейнере допишем метод регистрации:
Ссылка на реппозиторий.
В этом посте мы пытались показать, как благодаря использованию контекстов, интерфейсов и фабричного метода облегчить себе жизнь. Более детально о фабричном методе можно ознакомиться тут и тут.
В следующем посте расскажем о том, как мы «прикручивали» DUnit к FireMonkey. И напишем несколько тестов, некоторые из которых сразу вызовут ошибку.
Часть 3.
Часть 3.1
Здравствуйте.
В этой статье я продолжу рассказ о том, как мы пишем под FireMonkey. Будет добавлено 2 интересных объекта. Оба напомнят нам о векторной алгебре и тригонометрии. Также в посте будут показаны приемы из ООП, которыми мы пользуемся.
Ряд линий (отличаются только пунктиром, точка-тире, точка-точка, etc), которые мы добавили, были сделаны по аналогии с описанием предыдущих примитивов. Теперь время перейти к более сложным фигурам (включая составные).
Первый примитив, который мы добавим, будет линия со стрелкой (стрелкой будет рисоваться обычный треугольник, но меньших размеров).
Для начала введем треугольник который «смотрит вправо». Для этого унаследуем обычный треугольник и перепишем ему метод Polygon, который отвечает за координаты вершин.
function TmsTriangleDirectionRight.Polygon: TPolygon;
begin
SetLength(Result, 4);
Result[0] := TPointF.Create(StartPoint.X - InitialHeight / 2,
StartPoint.Y - InitialHeight / 2);
Result[1] := TPointF.Create(StartPoint.X - InitialHeight / 2,
StartPoint.Y + InitialHeight / 2);
Result[2] := TPointF.Create(StartPoint.X + InitialHeight / 2,
StartPoint.Y);
Result[3] := Result[0];
end;
Вот так выглядят наши треугольники:
Далее унаследуем так называемый «маленький треугольник»:
type
TmsSmallTriangle = class(TmsTriangleDirectionRight)
protected
function FillColor: TAlphaColor; override;
public
class function InitialHeight: Single; override;
end; // TmsSmallTriangle
Как видим, всё что мы сделали, это переопределили функции уникальные для нового треугольника.
Следующим классом добавим линию со стрелкой, которую унаследуем от обычной линии. В классе будет переопределена только процедура рисования самого примитива, то есть линию будет рисовать базовый класс, а вот треугольник — наследник.
procedure TmsLineWithArrow.DoDrawTo(const aCtx: TmsDrawContext);
var
l_Proxy : TmsShape;
l_OriginalMatrix: TMatrix;
l_Matrix: TMatrix;
l_Angle : Single;
l_CenterPoint : TPointF;
l_TextRect : TRectF;
begin
inherited;
if (StartPoint <> FinishPoint) then
begin
l_OriginalMatrix := aCtx.rCanvas.Matrix;
try
l_Proxy := TmsSmallTriangle.Create(FinishPoint);
try
// пока в целях эксперимента укажем поворот 0 градусов,
// что бы убедиться что треугольник рисуется правильно
l_Angle := DegToRad(0);
l_CenterPoint := TPointF.Create(FinishPoint.X , FinishPoint.Y);
// Запомнили начальную матрицу
l_Matrix := l_OriginalMatrix;
// Перенесли начало координат в точку вокруг которой будет осуществлен поворот
l_Matrix := l_Matrix * TMatrix.CreateTranslation(-l_CenterPoint.X, -l_CenterPoint.Y);
// Собственно - сам поворот
l_Matrix := l_Matrix * TMatrix.CreateRotation(l_Angle);
// Вернули начало координат на место
l_Matrix := l_Matrix * TMatrix.CreateTranslation(l_CenterPoint.X, l_CenterPoint.Y);
// собственно применяем нашу матрицу пространства к холсту
aCanvas.SetMatrix(l_Matrix);
// рисуем
l_Proxy.DrawTo(aCanvas, aOrigin);
finally
FreeAndNil(l_Proxy);
end; // try..finally
finally
// Так как мы отрисовали нужную нам фигуру, возвращаем начальную матрицу холсту.
aCanvas.SetMatrix(l_OriginalMatrix);
end;
end;//(StartPoint <> FinishPoint)
end;
Разбирать тут особо нечего, всё уже указано в комментариях, однако желающим вспомнить, что такое векторная алгебра и каким образом происходит работа с векторной графикой(перемещение, поворот различных фигур и т.д.), рекомендую замечательный пост на Хабре на эту тему, а также статьи «Векторы для чайников. Действия с векторами. Координаты вектора. Простейшие задачи с векторами» и «Линейная зависимость и линейная независимость векторов. Базис векторов. Аффинная система координат».
Как видим по рисунку, наш треугольник на данный момент рисуется только тогда, когда мы рисуем линию слева-направо:
Далее задача становится более интересной. Нам необходимо поворачивать треугольник, прямо перпендикулярно линии, которая его нарисовала. Для этого введем метод GetArrowAngleRotation, который будет рассчитывать угол поворота.
Для этого представим, что наша линия — это гипотенуза прямоугольного треугольника; далее найдем угол с катетом, который и будет углом поворота треугольника относительно линии:
function TmsLineWithArrow.GetArrowAngleRotation: Single;
var
l_ALength, l_CLength, l_AlphaAngle, l_X, l_Y, l_RotationAngle: Single;
l_PointC: TPointF;
l_Invert: SmallInt;
begin
Result := 0;
// Формула расчета растояний между двумя точками
l_X := (FinishPoint.X - StartPoint.X) * (FinishPoint.X - StartPoint.X);
l_Y := (FinishPoint.Y - StartPoint.Y) * (FinishPoint.Y - StartPoint.Y);
// Находим длинну гипотенузы прямоугольного треугольника
l_CLength := sqrt(l_X + l_Y);
l_PointC := TPointF.Create(FinishPoint.X, StartPoint.Y);
// Формула расчета растояний между двумя точками
l_X := (l_PointC.X - StartPoint.X) * (l_PointC.X - StartPoint.X);
l_Y := (l_PointC.Y - StartPoint.Y) * (l_PointC.Y - StartPoint.Y);
// Находим длинну катета
l_ALength := sqrt(l_X + l_Y);
// Угол в радианах
l_AlphaAngle := ArcSin(l_ALength / l_CLength);
l_RotationAngle := 0;
l_Invert := 1;
if FinishPoint.X > StartPoint.X then
begin
l_RotationAngle := Pi / 2 * 3;
if FinishPoint.Y > StartPoint.Y then
l_Invert := -1;
end
else
begin
l_RotationAngle := Pi / 2;
if FinishPoint.Y < StartPoint.Y then
l_Invert := -1;
end;
Result := l_Invert * (l_AlphaAngle + l_RotationAngle);
end;
Теперь наша линия выглядит так:
Следующий объект который мы добавим будет отвечать за перемещение фигур.
Алгоритм, которым мы воспользуемся:
1. Нам необходим метод для определения попадания точки в конкретную фигуру, скажем ContainsPt, для каждой фигуры; так как формулы для расчета попадания для каждой фигуры уникальны, пользуемся виртуальными функциями.
2. Следующий метод нам необходим для определения, в какую фигуру мы попали, если они пересекаются. Так как фигуры попадают в список по мере их появления на форме, то для случая пересечения фигур та из фигур, которая находится в начале списка, является последней появившейся, соответственно лежит «сверху». На самом деле, в этой логике есть прокол, однако по��а решим, что это правильно, а исправления оставим для следующего поста.
3. При первом нажатии в фигуру, в которую попали, мы должны изменить её контур или ряд других характеристик.
4. При втором нажатии мы должны переместить фигуру, в которую попали.
Сам класс перемещения будет наследоваться от стандартной фигуры, однако будет в себе хранить фигуру, которую он перемещает, и именно он при втором клике (в прошлом посте я описывал, в чём особенность рисования линий) будет перерисовывать фигуру.
Реализуем методы, которые я описал.
1. Метод определяет, попадает ли точка в фигуру(в нашем случае прямоугольник):
function TmsRectangle.ContainsPt(const aPoint: TPointF): Boolean;
var
l_Finish : TPointF;
l_Rect: TRectF;
begin
Result := False;
l_Finish := TPointF.Create(StartPoint.X + InitialWidth,
StartPoint.Y + InitialHeight);
l_Rect := TRectF.Create(StartPoint,l_Finish);
Result := l_Rect.Contains(aPoint);
end;
2. Этот метод при нажатии отвечает, нам на вопрос — в какую фигуру мы попали:
class function TmsShape.ShapeByPt(const aPoint: TPointF; aList: TmsShapeList): TmsShape;
var
l_Shape: TmsShape;
l_Index: Integer;
begin
Result := nil;
for l_Index := aList.Count - 1 downto 0 do
begin
l_Shape := aList.Items[l_Index];
if l_Shape.ContainsPt(aPoint) then
begin
Result := l_Shape;
Exit;
end; // l_Shape.ContainsPt(aPoint)
end; // for l_Index
end;
3. При первом нажатии в фигуру, в которую попали, мы должны изменить её контур или ряд других характеристик.
Для реализации следующего метода сделаем небольшой рефакторинг. Введем так называемый «контекст рисования»:
type
TmsDrawContext = record
public
rCanvas: TCanvas;
rOrigin: TPointF;
rMoving: Boolean; // - определяем, что текущий рисуемый примитив - двигается
constructor Create(const aCanvas: TCanvas; const aOrigin: TPointF);
end; // TmsDrawContext
Если мы укажем фигуре в контексте рисования что она «перемещаемая», то рисование будет происходить иначе.
procedure TmsShape.DrawTo(const aCtx: TmsDrawContext);
begin
aCtx.rCanvas.Fill.Color := FillColor;
if aCtx.rMoving then
begin
aCtx.rCanvas.Stroke.Dash := TStrokeDash.sdDashDot;
aCtx.rCanvas.Stroke.Color := TAlphaColors.Darkmagenta;
aCtx.rCanvas.Stroke.Thickness := 4;
end
else
begin
aCtx.rCanvas.Stroke.Dash := StrokeDash;
aCtx.rCanvas.Stroke.Color := StrokeColor;
aCtx.rCanvas.Stroke.Thickness := StrokeThickness;
end;
DoDrawTo(aCtx);
end;
4. При втором нажатии мы должны переместить фигуру, в которую попали.
Для начала введём фабричный метод который отвечает за построение фигуры(список фигур необходим нам для того, что бы TmsMover смог обратиться ко всем фигурам, которые нарисованы в рамках текущей диаграммы).
class function TmsShape.Make(const aStartPoint: TPointF; aListWithOtherShapes: TmsShapeList): TmsShape;
begin
Result := Create(aStartPoint);
end;
class function TmsMover.Make(const aStartPoint: TPointF;
aListWithOtherShapes: TmsShapeList): TmsShape;
var
l_Moving: TmsShape;
begin
// Ищём попадание в фигуру
l_Moving := ShapeByPt(aStartPoint, aListWithOtherShapes);
if (l_Moving <> nil) then
Result := Create(aStartPoint, aListWithOtherShapes, l_Moving)
else
Result := nil;
end;
Благодаря использованию классовой функции, мы принципиально разделили создание объекта перемещения и всех остальных фигур. Тем не менее, у этого подхода есть и отрицательная сторона. Например, мы ввели параметр создания aListWithOtherShapes, который совсем не нужен другим фигурам.
type
TmsMover = class(TmsShape)
private
f_Moving: TmsShape;
f_ListWithOtherShapes: TmsShapeList;
protected
procedure DoDrawTo(const aCtx: TmsDrawContext); override;
constructor Create(const aStartPoint: TPointF; aListWithOtherShapes: TmsShapeList; aMoving: TmsShape);
public
class function Make(const aStartPoint: TPointF; aListWithOtherShapes: TmsShapeList): TmsShape; override;
class function IsNeedsSecondClick: Boolean; override;
procedure EndTo(const aFinishPoint: TPointF); override;
end; // TmsMover
implementation
uses
msRectangle,
FMX.Types,
System.SysUtils;
constructor TmsMover.Create(const aStartPoint: TPointF; aListWithOtherShapes: TmsShapeList; aMoving: TmsShape);
begin
inherited Create(aStartPoint);
f_ListWithOtherShapes := aListWithOtherShapes;
f_Moving := aMoving;
end;
class function TmsMover.Make(const aStartPoint: TPointF;
aListWithOtherShapes: TmsShapeList): TmsShape;
var
l_Moving: TmsShape;
begin
l_Moving := ShapeByPt(aStartPoint, aListWithOtherShapes);
if (l_Moving <> nil) then
Result := Create(aStartPoint, aListWithOtherShapes, l_Moving)
else
Result := nil;
end;
class function TmsMover.IsNeedsSecondClick: Boolean;
begin
Result := true;
end;
procedure TmsMover.EndTo(const aFinishPoint: TPointF);
begin
if (f_Moving <> nil) then
f_Moving.MoveTo(aFinishPoint);
f_ListWithOtherShapes.Remove(Self);
// - теперь надо СЕБЯ удалить, так как после выполнения своей функции, мувер не нужен в общем списке
end;
procedure TmsMover.DoDrawTo(const aCtx: TmsDrawContext);
var
l_Ctx: TmsDrawContext;
begin
if (f_Moving <> nil) then
begin
l_Ctx := aCtx;
l_Ctx.rMoving := true;
f_Moving.DrawTo(l_Ctx);
end; // f_Moving <> nil
end;
initialization
TmsMover.Register;
end.
В контролере нам необходимо только изменить методы создания фигур:
procedure TmsDiagramm.BeginShape(const aStart: TPointF);
begin
Assert(CurrentClass <> nil);
FCurrentAddedShape := CurrentClass.Make(aStart, FShapeList);
if (FCurrentAddedShape <> nil) then
begin
FShapeList.Add(FCurrentAddedShape);
if not FCurrentAddedShape.IsNeedsSecondClick then
// - если не надо SecondClick, то наш примитив - завершён
FCurrentAddedShape := nil;
Invalidate;
end; // FCurrentAddedShape <> nil
end;
procedure TmsDiagramm.EndShape(const aFinish: TPointF);
begin
Assert(CurrentAddedShape <> nil);
CurrentAddedShape.EndTo(aFinish);
FCurrentAddedShape := nil;
Invalidate;
end;
Вызов CurrentAddedShape.EndTo(aFinish) в случае с мувером вызовет MoveTo, то есть переместит фигуру; перерисовку же, как видно выше, инициирует контролер:
procedure TmsMover.EndTo(const aFinishPoint: TPointF);
begin
if (f_Moving <> nil) then
f_Moving.MoveTo(aFinishPoint);
f_ListWithOtherShapes.Remove(Self);
// - теперь надо СЕБЯ удалить, так как фигура мувер не нужна в общем списке
end;
procedure TmsShape.MoveTo(const aFinishPoint: TPointF);
begin
FStartPoint := aFinishPoint;
end;
Так как контролер отвечает за логику поведение фигур, то вынесем метод проверки «попадания в фигуру» в контролер, а при создании объектов будем передовать функцию проверки:
type
TmsShapeByPt = function (const aPoint: TPointF): TmsShape of object;
...
class function Make(const aStartPoint: TPointF; aShapeByPt: TmsShapeByPt): TmsShape; override;
...
procedure TmsDiagramm.BeginShape(const aStart: TPointF);
begin
Assert(CurrentClass <> nil);
// Собственно сам вызов
FCurrentAddedShape := CurrentClass.Make(aStart, Self.ShapeByPt);
if (FCurrentAddedShape <> nil) then
begin
FShapeList.Add(FCurrentAddedShape);
if not FCurrentAddedShape.IsNeedsSecondClick then
// - если не надо SecondClick, то наш примитив - завершён
FCurrentAddedShape := nil;
Invalidate;
end;//FCurrentAddedShape <> nil
end;
Так как для создания объектов необходимо передать 2 параметра, создаем контекст «создания»:
type
TmsMakeShapeContext = record
public
rStartPoint: TPointF;
rShapeByPt: TmsShapeByPt;
constructor Create(aStartPoint: TPointF; aShapeByPt: TmsShapeByPt);
end;//TmsMakeShapeContext
Добавим интерфейсы, которые будет реализовывать контролер, а также добавим класс интерфейсного объекта. В будущем в нём мы реализуем собственный подсчет ссылок.
type
TmsInterfacedNonRefcounted = class abstract(TObject)
protected
function QueryInterface(const IID: TGUID; out Obj): HResult; stdcall;
function _AddRef: Integer; stdcall;
function _Release: Integer; stdcall;
end;//TmsInterfacedNonRefcounted
TmsShape = class;
ImsShapeByPt = interface
function ShapeByPt(const aPoint: TPointF): TmsShape;
end;//ImsShapeByPt
ImsShapesController = interface
procedure RemoveShape(aShape: TmsShape);
end;//ImsShapeRemover
Слегка изменим TmsMakeShapeContext:
type
TmsMakeShapeContext = record
public
rStartPoint: TPointF;
rShapesController: ImsShapesController;
constructor Create(aStartPoint: TPointF; const aShapesController: ImsShapesController);
end; // TmsMakeShapeContext
Детальнее об интерфейсах и особенностях работы с ними в Delphi рекомендую 2 интерестных поста:
18delphi.blogspot.com/2013/04/iunknown.html
habrahabr.ru/post/181107
Сделаем наш контролер(TmsDiagramm) унаследованным от TmsInterfacedNonRefcounted и интерфейсов и изменим в методе BeginShape одну строчку.
было:
FCurrentAddedShape := CurrentClass.Make(aStart, Self.ShapeByPt);
стало:
FCurrentAddedShape := CurrentClass.Make(TmsMakeShapeContext.Create(aStart, Self));
В случае с перемещением, метод EndTo который вызывается у мувера, примет такой вид:
procedure TmsMover.EndTo(const aCtx: TmsEndShapeContext);
begin
if (f_Moving <> nil) then
f_Moving.MoveTo(aCtx.rStartPoint);
f_Moving := nil;
aCtx.rShapesController.RemoveShape(Self);
// - теперь надо СЕБЯ удалить
end;
В прошлом посте я рассказывал о том, как мы спрятали «уникальные настройки» (цвет заливки, толщина линий и т.д.) в виртуальные методы, которые каждая фигура устанавливает самостоятельно. Например:
function TmsTriangle.FillColor: TAlphaColor;
begin
Result := TAlphaColorRec.Green;
end;
Все настройки фигур «упаковываем» в контекст:
type
TmsDrawOptionsContext = record
public
rFillColor: TAlphaColor;
rStrokeDash: TStrokeDash;
rStrokeColor: TAlphaColor;
rStrokeThickness: Single;
constructor Create(const aCtx: TmsDrawContext);
end;//TmsDrawOptionsContext
В классе TmsShape делаем виртуальную процедуру по аналогии с предыдущим пример. В будущем мы с легкостью расширим количество настроек уникальных для фигуры:
procedure TmsTriangle.TransformDrawOptionsContext(var theCtx: TmsDrawOptionsContext);
begin
inherited;
theCtx.rFillColor := TAlphaColorRec.Green;
theCtx.rStrokeColor := TAlphaColorRec.Blue;
end;
Благодаря контексту, убираем логику (мувер ли мы рисуем ?) из метода рисования и прячем её в конструктор записи:
constructor TmsDrawOptionsContext.Create(const aCtx: TmsDrawContext);
begin
rFillColor := TAlphaColorRec.Null;
if aCtx.rMoving then
begin
rStrokeDash := TStrokeDash.sdDashDot;
rStrokeColor := TAlphaColors.Darkmagenta;
rStrokeThickness := 4;
end // aCtx.rMoving
else
begin
rStrokeDash := TStrokeDash.sdSolid;
rStrokeColor := TAlphaColorRec.Black;
rStrokeThickness := 1;
end; // aCtx.rMoving
end;
После чего наш метод для рисования будут выглядеть так:
procedure TmsShape.DrawTo(const aCtx: TmsDrawContext);
var
l_Ctx: TmsDrawOptionsContext;
begin
l_Ctx := DrawOptionsContext(aCtx);
aCtx.rCanvas.Fill.Color := l_Ctx.rFillColor;
aCtx.rCanvas.Stroke.Dash := l_Ctx.rStrokeDash;
aCtx.rCanvas.Stroke.Color := l_Ctx.rStrokeColor;
aCtx.rCanvas.Stroke.Thickness := l_Ctx.rStrokeThickness;
DoDrawTo(aCtx);
end;
function TmsShape.DrawOptionsContext(const aCtx: TmsDrawContext): TmsDrawOptionsContext;
begin
Result := TmsDrawOptionsContext.Create(aCtx);
// Получаем уникальные настройки для каждой фигуры
TransformDrawOptionsContext(Result);
end;
Всё, что нам осталось для того, чтобы наши объекты перемещались, это написать каждой фигуре метод ContainsPt, который будет проверять, попала ли точка в фигуру. Обычная тригонометрия, все формулы есть на просторах интернета.
Слегка переделаем регистрацию объектов в контейнере. Сейчас каждый класс «регистрирует» сам себя. Вынесем регистрацию в отдельный модуль.
unit msOurShapes;
interface
uses
msLine,
msRectangle,
msCircle,
msRoundedRectangle,
msUseCaseLikeEllipse,
msTriangle,
msDashDotLine,
msDashLine,
msDotLine,
msLineWithArrow,
msTriangleDirectionRight,
msMover,
msRegisteredShapes
;
implementation
procedure RegisterOurShapes;
begin
TmsRegisteredShapes.Instance.Register([
TmsLine,
TmsRectangle,
TmsCircle,
TmsRoundedRectangle,
TmsUseCaseLikeEllipse,
TmsTriangle,
TmsDashDotLine,
TmsDashLine,
TmsDotLine,
TmsLineWithArrow,
TmsTriangleDirectionRight,
TmsMover
]);
end;
initialization
RegisterOurShapes;
end.
В контейнере допишем метод регистрации:
procedure TmsRegisteredShapes.Register(const aShapes: array of RmsShape);
var
l_Index: Integer;
begin
for l_Index := Low(aShapes) to High(aShapes) do
Self.Register(aShapes[l_Index]);
end;
procedure TmsRegisteredShapes.Register(const aValue: RmsShape);
begin
Assert(f_Registered.IndexOf(aValue) < 0);
f_Registered.Add(aValue);
end;

Ссылка на реппозиторий.
В этом посте мы пытались показать, как благодаря использованию контекстов, интерфейсов и фабричного метода облегчить себе жизнь. Более детально о фабричном методе можно ознакомиться тут и тут.
В следующем посте расскажем о том, как мы «прикручивали» DUnit к FireMonkey. И напишем несколько тестов, некоторые из которых сразу вызовут ошибку.
Часть 3.
Часть 3.1