
Задача корректной симуляции погодных эффектов тянется практически с самого основания игровой индустрии. Погода – неотъемлемая часть нашей жизни, а значит, игры без погодных эффектов не совсем полноценны. Именно поэтому редкая игра обходится без хотя бы очень примитивной погодной симуляции. Поскольку задача весьма стара, то имеется множество устаревших решений, которые и сейчас продолжают использоваться, несмотря на очевидно низкую эффективность. И если с обычным туманом всё просто, то реализация осадков вызывает определенные трудности.
Итак, что же такое дождь или снег в реальном мире?
Это миллиарды мелких частиц, которые более-менее равномерно заполняют собой пространство от самой земли и до облаков. В случае, если бы мы имели неограниченные вычислительные ресурсы – всё, что нужно было бы сделать для симуляции осадков — обработать этот миллиард частиц, равномерно распределенный по локации. Однако, наши вычислительные мощности весьма ограничены и даже миллион частиц в реальном времени посчитать возможно, только если локация будет состоять лишь из одних осадков, без ландшафта, объектов и всего остального. Что уж говорить о миллиарде.
В связи с этим в процессе реализации осадков перед нами возникают три отдельных задачи:
- Уменьшение количества частиц с миллиарда до приемлемых 20-50 тысяч.
- Уменьшение объёма вычислений на каждую частицу до минимума.
- Перенос всех вычи��лений на GPU.
Для начала рассмотрим, как мы будем этого добиваться:
Уменьшать количество частиц мы будем на основе простого умозаключения: наблюдатель не видит весь миллиард частиц. Он не видит частицы позади себя, слишком далеко внизу и вверху. Это уже обрезает количество частиц в 3-4 раза. Но 200 миллионов тоже многовато. Тут нам на помощь приходит небольшая хитрость. Дело в том, что частицы очень маленькие и в реальности уже на расстоянии нескольких метров превращаются в равномерную пелену. Поэтому «честно» нам нужно отрисовывать только частицы перед наблюдателем на расстоянии около 10 метров. 50 000 частиц в таких условиях хватает, чтобы создать видимость очень плотного снегопада. Также, важно понимать, что в реальном мире размер частиц измеряется в миллиметрах. В случае компьютерной симуляции мы можем безболезненно увеличить размер частиц до нескольких сантиметров и это всё равно будет хорошо смотреться, т.к. у наблюдателя нет возможности рассмотреть частицы и сравнить их размеры с предметами вокруг.
Вот так выглядит локация с осадками в виде снега со следующими настройками: Количество частиц 25000 в пределах 15 метров, размер частицы – 10 сантиметров, на расстоянии от 20 до 100 метров белый туман плотностью 80%.

Вот та же локация с отключенными осадками:

Несмотря на то, что размер частиц неестественно большой, наблюдателем это воспринимается абсолютно нормально — ведь он не может оценить расстояние до частицы, и создается ощущение, что большие частицы большие потому, что находятся очень близко. Хотя на самом деле это не так.
Вторая важная задача – уменьшение вычислений для каждой частиц до минимума. Даже 25000 частиц в каждом кадре – это ощутимая нагрузка. Поэтому даже небольшая оптимизация имеет значение. Итак, вспомним: какие вычисления нам нужно проводить над частицей, если считать её честно:
- Появление в случайных координатах XY объёма
- Ускорение за счёт гравитации
- Сопротивление воздуха по Z
- Сопротивление воздуха по X,Y (ветер)
- Пересечение с геометрией (чтобы частицы не проходили сквозь препятствия, например крышу дома, где находится наблюдатель).
Эти параметры весьма важны, если мы работаем над точной симуляцией. Однако, в играх нам важна визуальная составляющая, а не точность физической симуляции. У наблюдателя нет возможности проследить поведение одной конкретной частицы, поэтому можно безболезненно избавиться от случайности и честного расчёта. Даже если частица будет из цикла в цикл проходить один и тот же путь без изменений – наблюдатель этого не заметит, т.к. рядом будут двигаться ещё 24999 частиц по своим путям (пусть даже также зацикленным).
Поэтому:
- Частица всегда появляются в одних и тех же координатах относительно блока. Эти координаты – координаты, переданные через вершинный буфер.
- Ускорение и сопротивление по Z мы игнорируем и считаем, что они друг друга перекрывают. То есть частица движется с постоянной скоростью.
- Игнорируем честные расчеты и просто прибавл��ем к первоначальным XY координатам частицы скорость ветра* время.
- Всю статичную геометрию запекаем в карту высот и просто проверяем Z-позицию частицы и высоту частицы в координатах XY. Если частица опустилась ниже высоты в этой точке – её не рисуем.
Стоит отметить, что упрощённое пересечение с геометрией не всегда работает, а иногда даже может создавать артефакты. Визуально это выглядит как появление частиц из пустоты.
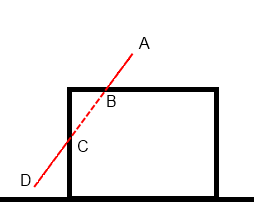
Наша частица начинает свой путь в точке «A», расположенной над домом, и пока она опускается до точки «B» – всё нормально. Она выше геометрии. Как только она пересекла высоту «B», то стала невидимой, т.к. находится под крышей. Это продолжается до тех пор, пока она не пройдет точку «C». Из-за влияния ветра частица переместилась за пределы дома и опять оказалась выше геометрии, вследствие чего она снова становится видимой. Визуально это выглядит так, будто частицы «появляются» из стены дома. Это достаточно неприятный артефакт и стоит иметь в виду, что он существует. Если попытаться «честно» посчитать пересечение вектора частицы с геометрией мы рискуем очень сильно замедлить работу системы осадков. Но есть достаточно простой хинт: модифицировать карту высот в соответствии с отклонение частиц из-за ветра:
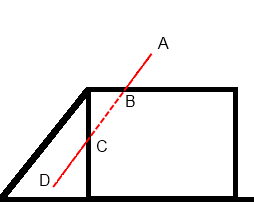
Единственный минус такого решения — придется перестраивать карту высот при изменении ветра.
Игрострой всегда был компромиссом между артефактами и скоростью и этот случай — как раз один из примеров такого компромисса. Артефакт тем более заметен, чем выше скорость ветра.
Последний этап оптимизации – перенос вычислений на GPU. Собственно, никаких особых вычислений после предыдущего шага у нас и не осталось.
XY координаты вычисляются из начальных координат плюс смещение, добавленное ветром:
XY = Start.xy + Wind*Time;
Z координата вычисляется вычитанием из начальной координаты скорости падения, умноженной на время:
Z = Start.z – Speed*Time
Ну, и последнее – видимость частицы определяется сравнением полученной Z координаты с высотой геометрии в этой точке:
IsVisible = MapHeight(XY)<Z
Все эти три операции без проблем переносятся на GPU. Есть ещё расчёт прозрачности с учётом дальности от наблюдателя, применение освещения, и прочие мелочи. Но они и так применяются на GPU и, очевидно, не станут проблемой при переносе.
Прежде чем перейти к описанию конкретной реализации всего вышеописанного, стоит остановиться ещё на одном важном аспекте реализации. А именно, на определении того, в каком месте мира рисовать созданный нами блок частиц и какой формы он должен быть.
Первое, что приходит в голову при реализации – часть цилиндра, с центром в координатах наблюдателя и срезами по граням фрустума.

Это очень соблазнительный вариант, т.к. генерируя частицы только в пределах получившегося куска цилиндра, мы можем работать только с зоной, которую видит наблюдатель. То есть почти все 50000 сгенерированных частиц будут на экране! Очень экономно! Но всё ломается, когда мы даём наблюдателю возможность перемещать и вращать камеру. Для того, чтобы частицы остались внутри фрустума, нам придётся перемещать цилиндр вместе с наблюдателем. То есть независимо от того, как двигается и крутится наблюдатель – он всегда видит одни и те же частицы! Это никуда не годится. Поэтому мы остановимся на другом варианте, в нём достаточно много вырожденных частиц, но при этом вращение и перемещение камеры не ломает работу системы частиц и при перемещении и вращении камеры создаётся ощущение, что мы видим новые частицы, хотя на самом деле это всё тот же блок частиц.
Идея в том, что мы работаем с зоной в виде куба. При первоначальной инициализации частицы в случайном порядке размещаются на XoY плоскости в соответствии с размерами куба.
Координаты частиц заполняют собой квадратный кусок в начале координат мира размером с блок:

Черными точками отмечены координаты частиц, как есть. Красные – это те же частицы, только смещенные на размер блока. Как это работает: у нас есть фрустум наблюдателя. Мы берём и вписываем наш куб во фрустум. Основных условий вписывания три:
1) Блок не вращается. Вписывание проводится только перемещением.
2) Координаты наблюдателя должны содержаться в блоке.
3) Расстояние от наблюдателя до пересечения обеих граней фрустума со сторонами блока должно быть максимально одинаковое.
После вписывания блока во фрустум мы получаем примерно такую картину:

Фрустум гораздо больше нашего блока, но это неважно, т.к. частицы должны быть только в нескольких первых метрах от наблюдателя.
После того как мы получили координаты вписанного блока, считаем XY координаты для каждой частицы с учётом применения ветра. Для простоты в этом примере я буду считать, что ветра нет и, соответственно, координаты частиц не изменили свои XY координаты.

Каждую частицу мы смещаем так, чтобы она попала во вписанный блок. Для этого мы смещаем частицы по X и Y, но смещаем не плавно, а с шагом, равным размеру блока.
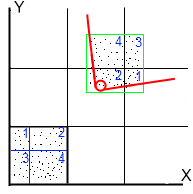
Получится, что частицы перемещаются не каждая сама по себе, а блоками. Например частицы, попавшие в блок «1» переместятся по X на 2 размера, а по Y на 1.
Таким образом, все частицы окажутся внутри зоны на своих проекциях в соответствии со смещением на сетке.
Перемещаясь, наблюдатель будет смещать зону и частицы, соответственно, будут перемещаться на новые проекции.
Например, если из текущей позиции наблюдатель сместится по X вправо, то блоки «4» и «2» уменьшатся, а блоки «3» и «1», наоборот, увеличатся. Частицы, выпавшие из зоны слева, перепрыгнут вправо. В итоге, перемещаясь, наблюдатель будет видеть всё новые частицы, хотя на самом деле это старые частицы, выпавшие из зоны. Та же ситуация с вращением, только зона будет меняться не из-за изменения позиции наблюдателя, а из-за изменения границ фрустума.
Практическая реализация
Все частицы осадков рисуются за один DIP. Буфер вершин инициализируется один раз статически и более не меняется. Каждая частица представляется одной вершиной, со случайными XY в пределах блока. Геометрический шейдер создаёт из вершины частицу. Сделано на примере снега. Для дождя нужно делать не сферические билборды, а цилиндрические. И, соответственно, частица не квадратная, а прямоугольная.
Глобально для всех частиц нам понадобятся следующие данные:
mat4 ModelViewProjectionMatrix; — проекционно-модельно-видовая матрица для перевода координат из пространства модели в пространство камеры и проецирования на плоскость экрана;
float Time; — глобальное время в секундах;
float Speed; — скорость падения частицы;
float Top; — высота, с которой начинают падать частицы;
float Bottom; — высота, на которой заканчивают падать частицы;
float CircleTime; — время, за которое частица перемещается с самой верхней точки в самую нижнюю;
vec2 Wind; — скорость ветра;
float TileSize; — размер блока;
vec2 Border; — координаты блока. Левый верхний угол блока. Правый нижний – это Border+vec2(TileSize,TileSize);
float ParticleSize; — размер частицы;
sampler2D Texture; — текстура частицы.
Атрибуты каждой частицы:
vec2 Position; — позиция. Это значение задаётся случайно в пределах блока. Z-координата не задаётся, т.к. она вычисляется внутри шейдера;
float TimeShift; — смещение частицы во времени относительно 0. Значение задаётся случайно в пределах CircleTime.
Добавив это значение к Time, получим случайную стартовую позицию частицы;
float SpeedScale; — случайное значение в пределах от 0.9 – 1.1. Умножив на это значение Speed, получим немного разную скорость у каждой ча��тицы.
Вершинный шейдер:
uniform mat4 ModelViewProjectionMatrix; uniform float Time; uniform float Speed; uniform float Top; uniform float Bottom; uniform float CircleTime; // (Top-Bottom)/Speed uniform vec2 Wind; uniform float TileSize; uniform vec2 Border; in vec2 Position; in float TimeShift; in float SpeedScale; out vec4 Position3D; void main(void) { float ParticleCircleTime = CircleTime / SpeedScale; float CurrentProgress = mod(Time + TimeShift, ParticleCircleTime); vec3 Pos = vec3(Position.xy + Wind*CurrentProgress , Top - Speed*SpeedScale*CurrentProgress); Pos.x = mod(Pos.x, TileSize); Pos.y = mod(Pos.y, TileSize); float c; c = floor(Border.x/TileSize); if (c*TileSize+Pos.x < Border.x) Pos.x = Pos.x + (c+1)*TileSize; else Pos.x = Pos.x + c*TileSize; c = floor(Border.y/TileSize); if (c*TileSize+Pos.y < Border.y) Pos.y = Pos.y + (c+1)*TileSize; else Pos.y = Pos.y + c*TileSize; Position3D = ModelViewProjectionMatrix * vec4(Pos,1.0); }
Геометрический шейдер:
layout(points) in; layout(triangle_strip, max_vertices=12) out; const vec3 up = vec3(0.0,1.0,0.0); const vec3 right = vec3(1.0,0.0,0.0); uniform vec2 ParticleSize; in vec4 Position3D []; out float TexCoordX; out float TexCoordY; void main(void) { vec3 u = up * vec3(ParticleSize.y); vec3 r = right * vec3(ParticleSize.x); vec3 p = Position3D[0].xyz; float w = Position3D[0].w; gl_Position = vec4 ( p - u - r, w ); TexCoordX = 0.0; TexCoordY = 1.0; EmitVertex (); gl_Position = vec4 ( p - u + r, w ); TexCoordX = 1.0; TexCoordY = 1.0; EmitVertex (); gl_Position = vec4 ( p + u + r, w ); TexCoordX = 1.0; TexCoordY = 0.0; EmitVertex (); EndPrimitive (); // 1st triangle gl_Position = vec4 ( p + u + r, w ); TexCoordX = 1.0; TexCoordY = 0.0; EmitVertex (); gl_Position = vec4 ( p + u - r, w ); TexCoordX = 0.0; TexCoordY = 0.0; EmitVertex (); gl_Position = vec4 ( p - u - r, w ); TexCoordX = 0.0; TexCoordY = 1.0; EmitVertex (); EndPrimitive (); // 2nd triangle }
Фрагментный шейдер:
uniform sampler2D Texture; in float TexCoordX; in float TexCoordY; out vec4 color; void main(void) { color = texture(Texture, vec2(TexCoordX, TexCoordY)); }
Рассмотрим подробнее, что делают приведённые шейдеры.
Все основные операции проводятся в вершинном шейдере. Геометрический шейдер распаковывает точку в объёмную частицу, а фрагментный просто наносит текстуру. В связи с простотой кода, геометрический и фрагментный шейдер рассматриваться не будут.
Рассмотрим вершинный шейдер:
Первое, что нам необходимо сделать — это выяснить, в какой же позиции сейчас находится частица. Позиция у нас привязана ко времени, поэтому время мы и должны вычислить. Это делается двумя операциями:
float ParticleCircleTime = CircleTime / SpeedScale;
float CurrentProgress = mod(Time + TimeShift, ParticleCircleTime);
Первой строкой мы приводим общее время цикла к циклу конкретной частицы. Т.к. цикл у нас зависит от скорости, а скорости отличаются на SpeedScale, то всё, что нам нужно сделать – это разделить общее время цикла на коэффициент скорости.
Второй строкой мы получаем текущее глобальное время частицы, делим на время одного цикла и получаем остаток от деления CurrentProgress. Это и есть время, прошедшее со старта текущего цикла для конкретной частицы.
Следующий этап – вычисление позиции в соответствии с прошедшим временем. Для вычисления XY нужно прибавить к стартовой позиции смещение, полученное от ветра, для Z – отнять скорость падения, умноженную на время.
vec3 Pos = vec3(Position.xy + Wind*CurrentProgress, Top — Speed*SpeedScale*CurrentProgress);
Так как из-за ветра частица могла улететь за пределы блока, нам нужно вернуть её в блок:
Pos.x = mod(Pos.x, TileSize);
Pos.y = mod(Pos.y, TileSize);
В итоге мы получаем координаты частицы в пределах блока.

Однако, нам нужно чтобы частицы были не в начале координат, а вокруг наблюдателя! В связи с этим, мы перемещаем частицы в зону, описанную вокруг фрустума:
c = floor(Border.x/TileSize);
if (c*TileSize+Pos.x < Border.x)
Pos.x = Pos.x + (c+1)*TileSize;
else
Pos.x = Pos.x + c*TileSize;
c = floor(Border.y/TileSize);
if (c*TileSize+Pos.y < Border.y)
Pos.y = Pos.y + (c+1)*TileSize;
else
Pos.y = Pos.y + c*TileSize;

Полученные координаты проецируем на экран: Position3D = ModelViewProjectionMatrix * vec4(Pos,1.0);
Далее уже геометрический шейдер распакует вершину в частицу.
Приведённый код является самой простой реализацией снега. Добавление глобального освещения, точечных источников света и пересечения с геометрией — задачи достаточно простые, думаю вы с ними справитесь самостоятельно. Также не забывайте, что одних частиц не достаточно для создания ливня или снегопада, т.к. частиц не очень много. В этой ситуации поможет туман, с помощью которого создается ощущение снежной или дождевой пелены.
Примечание:
Данная статья написана в рамках так и не опубликованной книги несколько лет назад.
После завершения работы над достаточно большим проектом я оглянулся назад и увидел, что за годы разработки возникали задачи, о которых можно интересно рассказать. В результате чего появилась книга. Книга была написана и отредактирована еще в 2012 году, но нигде не публиковалась, т.к. была не ясна её целевая аудитория.
Сегодня наткнулся на текст этой книги и подумал, что, возможно, некоторые главы из неё будут интересны сообществу Хабра.
В качестве теста публикую главу, посвящённую реализации погодных эффектов. Если статья будет позитивно встречена сообществом, позднее опубликую ещё пару глав.