Данный пост использует попытку ввода измерения терминов в сферической системе координат.
Вводятся понятия абстрактности, фазы деятельности, а также группы и периоды сложности.
Описывается графическая нотация для моделирования, основанная на предлагаемом выделении групп терминов.
1. Сферическая модель мировоззрения
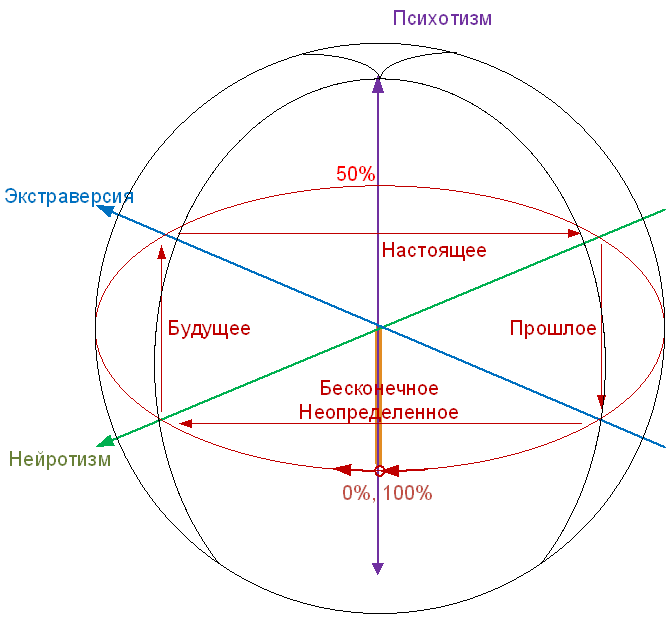
Ганс Юрген Айзенк разработал систему координат для измерения психологических характеристик человека, состоящую из шкал экстраверсии, нейротизма и психотизма.
Данные шкалы используются в психологических тестах по определению типа темперамента человека, а также в тестах по измерению коэффициента интеллекта
Такую систему измерений можно считать трехмерной декартовой системой координат, а, следовательно, можно перейти от декартовых координат к полярным.
Рис. 1 Связь декартовых и полярных координат
В полученной системе координат в этой статье не будет использоваться расстояние от центра системы координат, но будет использоваться угол между точкой и горизонтальной плоскостью, проходящей через центр (аналогично широте в географических координатах Земли), и угол проекции на горизонтальную плоскость (аналогично долготе в географических координатах Земли).
Для полученных шкал сферических координат введем следующие
единицы измерения:
- абстрактность, соответствующую долготе, выражаемую в процентах, и принимающую значение 0% для нижнего полюса, 100% для верхнего полюса, и 50% для точки, расположенной на круге, образованном пересечением сферы и горизонтальной плоскостью;
- фаза, соответствующая долготе, выражаемая в процентах, увеличивающая в направлении часовой стрелки и принимающая значение 0%, а также 100% для биссектрисы между положительным направлением оси нейротизма и отрицательным направлением оси экстраверсии (интроверсией)
Развернем данную сферическую систему координат на плоскость, как это делалось при изготовлении первых карт Земли (цилиндрическая проекция Меркатора). При этом верхний и нижний полюсы переходят в горизонтальные линии.
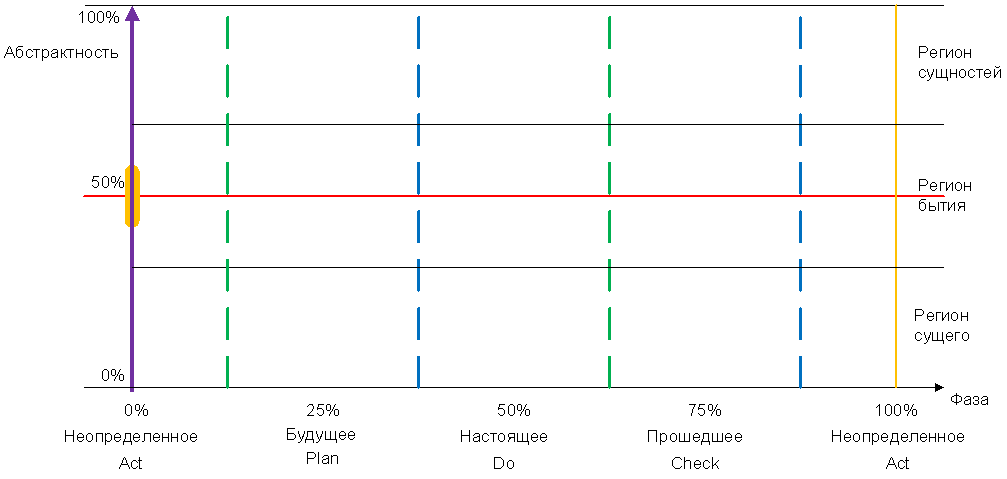
Рис. 2 Полярные координаты с выделенными регионами
Автором была исследована возможность использования полученной системы координат для определения численных значений терминов методик моделирования предметной области, в частности, распространенных методик SADT и UML, при этом были получены положительные результаты.
2. Периодическая таблица сложности
По мере расширения списка анализируемых терминов появилась потребность выделения новых горизонтальных уровней на шкале абстрактности, в которых была выявлена группировка по типу фаз сигмоиды.
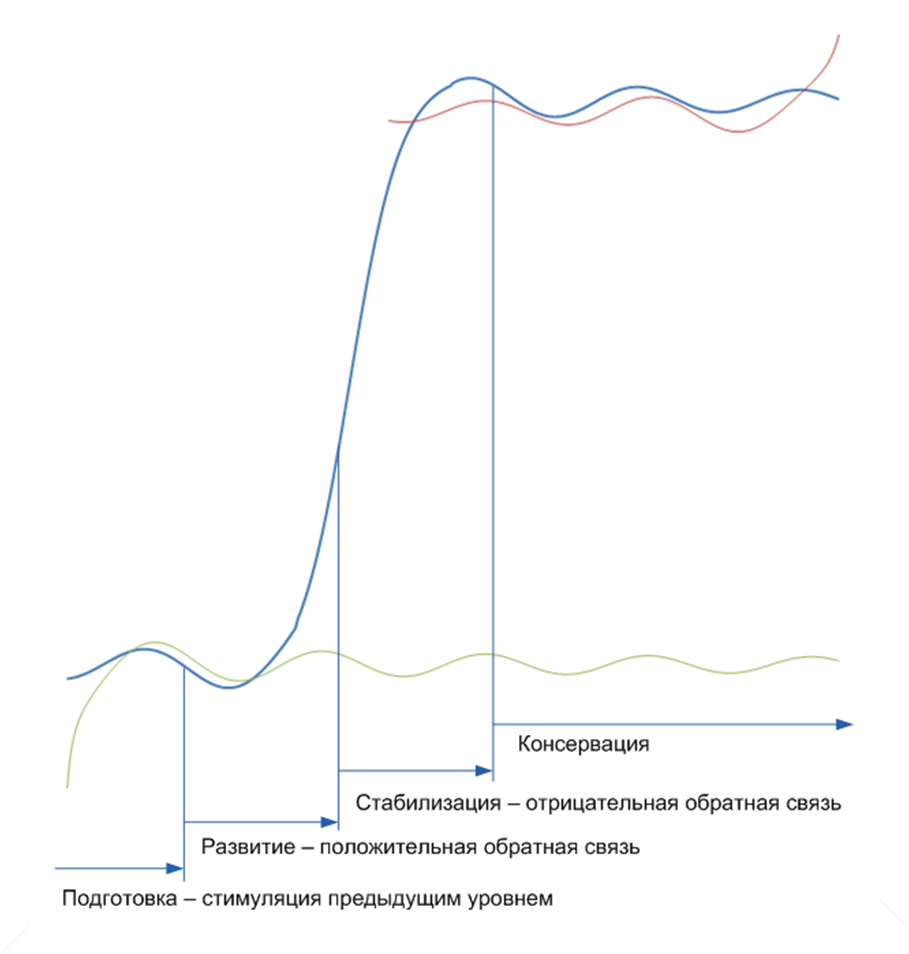
Рис. 3 Усложнение в виде цепочки сигмоид
Для отдельных элементов усложнения (по аналогии с периодической таблицей химических элементов Д.И. Менделеева) предлагается использование терминов группа сложности и период сложности.
Периоды сложности показаны на рисунке 3. Предлагается
следующее объяснение для их выделения:
- подготовительный этап характеризуется потребностями компенсации
возмущений от предыдущего уровня; - этап развития связан с появлением положительной обратной связи, стимулирующей развитие;
- этап стабилизации связан с появлением отрицательной обратной связи, ограничивающей развитие;
- - этап консервации характеризуется стабильным существованием, и не входит в отдельные группировки терминов.
На данный момент выделено три группы сложности терминов моделирования. Группы сложности симметрично распространяются от верхнего и нижнего полюсов.
При этом предлагается соответствие групп и периодов с предметами университетского образования (Таблица 1).
Таблица 1.
Предлагаемая классификация образовательных предметов
| Группа |
Период |
Абстрактные |
Конкретные |
| Случайное |
Стабилизация |
Логика |
Квантовая физика |
| Элементы |
Подготовка |
Математика |
Физика |
| Развитие |
Философия |
Химия |
|
| Стабилизация |
Культуроведение |
Биология |
|
| Процессы |
Подготовка |
Политология |
Психология |
| Развитие |
Менеджмент |
Социология |
|
| Стабилизация |
Маркетинг |
Экономика |
|
| Общество |
Подготовка |
Связи с общественностью |
Синергетика |
| Развитие |
Управление качеством |
Технология |
Для периода «развитие» группы «случайное» предлагаются термины будущее для абстрактного и прошлое для конкретного.
2. Графические примитивы туннельного моделирования
Для отображения уровня сложности предлагается система обозначений, на основе меток с левой стороны прямоугольного элемента моделирования. Для обозначений предлагается использование пар треугольников. Треугольники в паре могут иметь закрашенное и не закрашенное состояние, что позволяет использовать аналог двоичного кода.
Для построения блок-схем программ необходимо также иметь элементы для операций ветвления и цикла. Эти элементы приведены на рисунках 5 и 6.
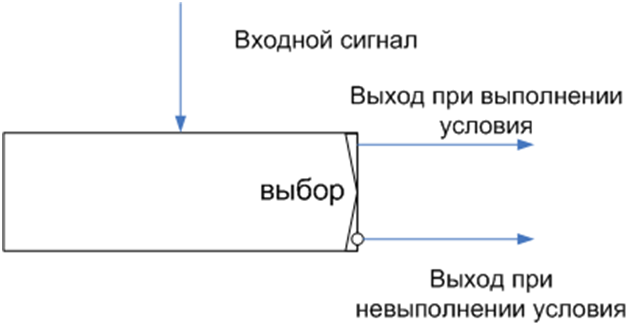
Рисунок 5 Моделирование выбора из двух альтернатив

Рисунок 6. Моделирование цикла
Фазы, соответствующие элементам цикла Деминга-Шугарта -Act-Plan-Do-Check-
обозначаются специальными символами в правой части прямоугольника элемента
моделирования.

Рисунок 7. Элементы цикла Деминга-Шухарта
Основной настраиваемый элемент моделирования содержит меню, позволяющее выбрать особенности изображения.
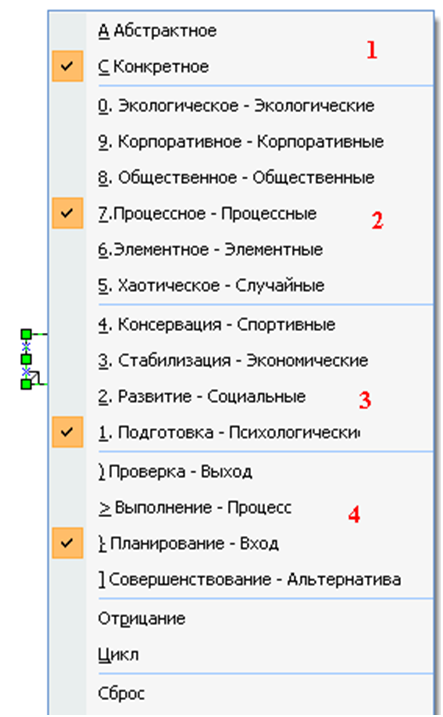
Рис. 8. Меню настройки вида прямоугольника
Уточнение вида изображения производится последовательным уточнением по группам пунктов меню:
- абстрактность
- группа сложности
- период сложности
- элемент цикла Деминга-Шухарта
Иерархической декомпозиции могут быть подвергнуты как прямоугольники, так и стрелки
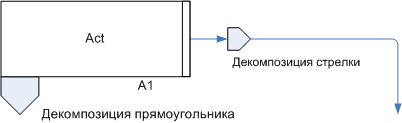
Рис. 9. Представление стрелок декомпозиции
Остальные элементы можно заимствовать из устоявшихся методик моделирования – UML, SADT, BPMN, ДРАКОН, Archimate.
4. Предложение по проекции бытия на сферу мировоззрения
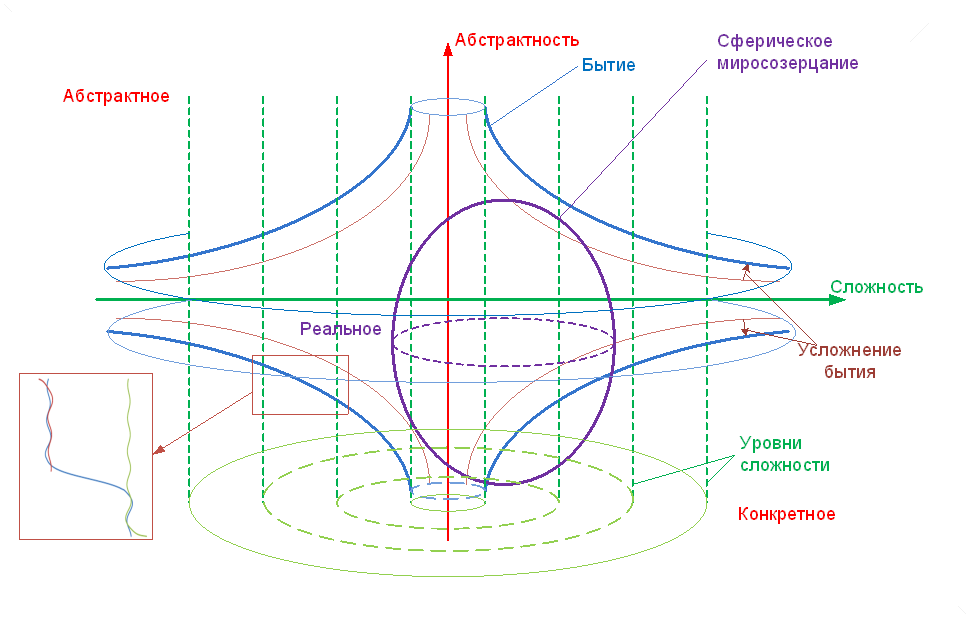
При рассмотрении сферической модели возникает парадокс между сложностью центральной области и «недостатком места» для отображения этой сложности.
Для объяснения такого несовпадения можно предположить гиперболическую зависимость сложности по мере удаления от полюсов.
Иллюстрацией такого взгляда может служить рисунок 10:
Рисунок 10. Проекция бытия на сферу миросозерцания
С учетом перспективных областей можно предложить расширение классификации наук Огюста Конта с учетом симметричного дуализма Рене Декарта

Рисунок 11. Предложение по последовательности анализа
Краткий справочник по элементам нотации приведен на рис.12.
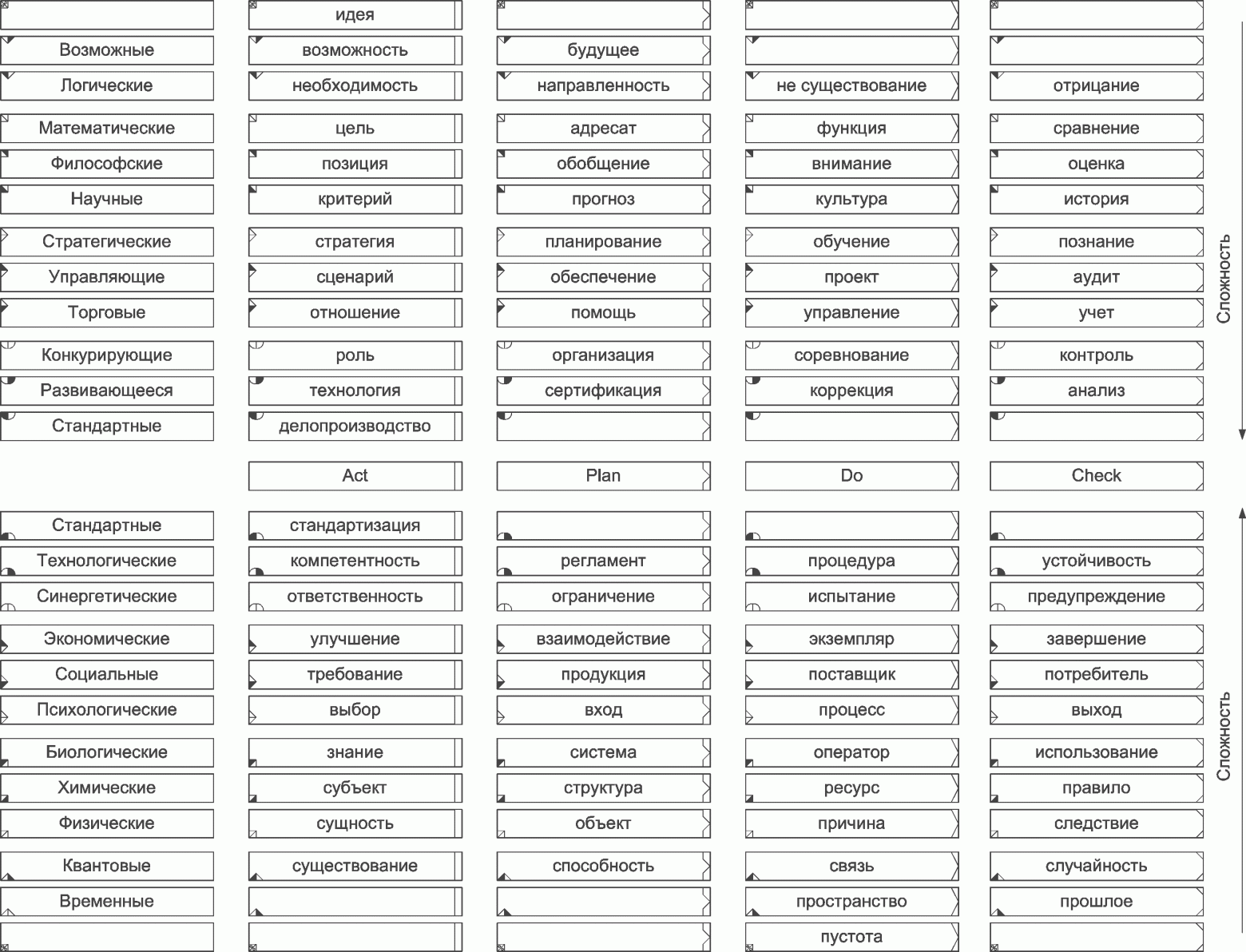
Рисунок 12. Обозначения для разделов знания
Темы на Хабрахабре:
Туннельное моделирование — версия 1.0
Соотношение абстрактности и сложности при моделировании
habrahabr.ru/post/254275
Уровни сложности моделирования
habrahabr.ru/post/238599
Презентация идеологии
habrahabr.ru/post/177131
Преобразование подхода Захмана
habrahabr.ru/post/267749
ISO 15926 vs Семантика: сравнительный анализ семантических моделей
habrahabr.ru/post/178973
Создаем новую OS. Действительно новую, реально операционную, и правда – систему
habrahabr.ru/company/intel/blog/300884
Литература:
ru.wikipedia.org/wiki/Теория_функциональных_систем
ru.wikipedia.org/wiki/Айзенк,_Ганс_Юрген
Карамышев С.В. Куда вывезет S-кривая?
www.metodolog.ru/01493/01493.html
Жаров А. Будущее. Эволюция продолжается
fan.lib.ru/z/zharow_a/2050buduschee.shtml
Нариньяни А.С. Между Знанием и Незнанием – Наивная Топография
viperson.ru/articles/aleksandr-narinyani-mezhdu-znaniem-i-neznaniem-naivnaya-topografiya
Диффузия инноваций в Википедии
ru.wikipedia.org/wiki/Диффузия_инноваций
Пятифакторная модель личности человека
https://ru.wikipedia.org/wiki/Большая_пятёрка_(психология)