Comments 12
Да, я делала преобразования над искусственными сигналами, чтобы показать, что и в идеальном случае не все гладко.
Согласна, что очень многое зависит от того, как именно исполнялось проиведение, я вскользь упомянула об этом в конце статьи. Моя же цель заключалась в том, чтобы показать, что уже на этапе дискретизации сигнала существует вероятность ошибки.
Согласна, что очень многое зависит от того, как именно исполнялось проиведение, я вскользь упомянула об этом в конце статьи. Моя же цель заключалась в том, чтобы показать, что уже на этапе дискретизации сигнала существует вероятность ошибки.
Если исходный «аккорд» представляет собой сумму незатухающих «чистых синусоид» (по форме) и в выборке укладывается целое число периодов всех (каждой) составляющих аккорд «синусоид», то возможно произвести прямое и обратное преобразование Фурье и восстановить исходный сигнал без искажений.
dt = 0.001;
T = 1;
t=0:dt:T;
Зачем же вы пытаетесь сигнал с частотой 3440 Гц дискретизовать с частотй 1000 Гц? Конечно ничего не получится.
FFT также работает с комплексными числами и отличается тем, что размер самого преобразования обязательно является степенью двойки,— это неправда. Можно и степень тройки, и любая комбинация небольших простых множителей.
Согласна, допустила значимую ошибку. Конечно же по теореме Котельникова здесь точность совершенно не гарантируется.
Попробовала запустить тот же код, поменяв значение параметра dt на 0.0001. График получился следующий:
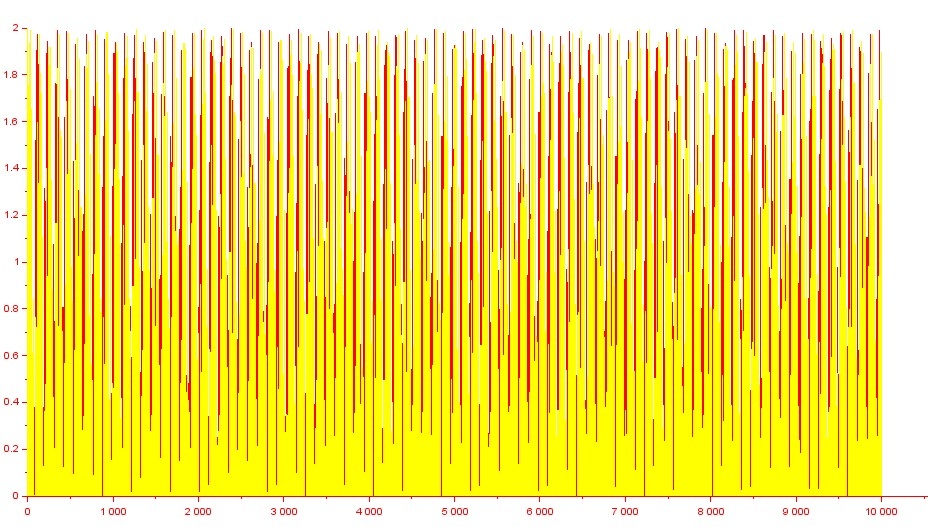
Не похоже, что это сдвиг по фазе.
Попробовала запустить тот же код, поменяв значение параметра dt на 0.0001. График получился следующий:

Не похоже, что это сдвиг по фазе.
И в первом, и в этом варианте выглядит так, будто новый сигнал — зеркальное отражение исходного. Не знаю, на каком языке вы пишете, но вы уверены, что вам нужно
fft(x, -1), а не что-то вроде ifft(x)? Дело в том, что дважды применённое прямое преобразование — это в точности разворот вектора.Действительно, если почитать документацию (автор использует Scilab), то там про второй параметр написано:
Так что действительно, автор дважды применила прямое преобразование.
sign
an integer. with possible values 1 or -1. Select direct or inverse transform. The default value is -1 (direct transform).
Так что действительно, автор дважды применила прямое преобразование.
обычный синус имеет ограниченный спектр, неограничен по времени.
прекрасно представляется гармониическим рядом из одного слагаемого.
при этом балуясь с ффт, если не понимать математики этого процесса, можно получать весьма неожиданные результаты.
рекомендую ознакомление с полной формулировкой теоремы Котельникова.
прекрасно представляется гармониическим рядом из одного слагаемого.
при этом балуясь с ффт, если не понимать математики этого процесса, можно получать весьма неожиданные результаты.
рекомендую ознакомление с полной формулировкой теоремы Котельникова.
Вот результаты работы программы — график исходного сигнала, спектр и восстановленный сигнал — обратное преобразование Фурье.
Можно увидеть, что сигнал полностью восстанавливается.
Сигнал задается как сумма трех гармоник
xdata(i) = 16 * COS(th * 30) 'amp & Hz
xdata(i) = xdata(i) + 6 * COS(th * 6) 'amp & Hz
xdata(i) = xdata(i) + 4 * SIN(th * 14) 'amp & Hz


Можно увидеть, что сигнал полностью восстанавливается.
Сигнал задается как сумма трех гармоник
xdata(i) = 16 * COS(th * 30) 'amp & Hz
xdata(i) = xdata(i) + 6 * COS(th * 6) 'amp & Hz
xdata(i) = xdata(i) + 4 * SIN(th * 14) 'amp & Hz


Sign up to leave a comment.
Ограниченность преобразования Фурье или почему стоит доверять своему слуху