Друзья, на прошедшей в прошлом году конференции PG Day'15 Russia один из наших докладчиков, Joseph Conway, представил интересный материал об использовании созданного и поддерживаемого им уже больше десяти лет расширения PL/R, которое позволяет использовать язык для статистического анализа R внутри всеми любимой базы данных. Хочу предложить вашему вниманию follow-up статью, созданную на основе материалов, представленных в докладе Joe. Задача данной публикации — обзорно познакомить вас с возможностями языка PL/R. Надеюсь, что вы найдете представленную здесь информацию полезной для себя.
Последние тенденции в области Big Data поощряют сближение аналитики и данных, в то время как PL/R ненавязчиво предоставляет такой сервис вот уже 12 лет! Если вдруг вы не в курсе, PL/R – это расширение для PostgreSQL, позволяющее использовать R, язык для математических расчетов, прямо из PostgreSQL для того, чтобы легко и просто получать развернутую аналитику. Расширение доступно и активно совершенствуется с 2003 года. Оно работает со всеми поддерживаемыми версиями PostgreSQL и со всеми свежими версиями R. Тысячи людей во всем мире уже оценили его удобство и эффективность. Давайте же разберемся, что такое PL/R, обсудим достоинства и недостатки такого подхода к анализу данных и рассмотрим несколько примеров для наглядности.
Для начала дадим определения базовым понятиям. R – это язык программирования для статистической обработки данных и работы с графикой, а также свободная программная среда вычислений с открытым исходным кодом. А PostgreSQL – это мощная свободная объектно-реляционная система управления базами данных, которая активно разрабатывается вот уже более 25 лет и заработала отличную репутацию благодаря своей надежности, а также корректности и целостности данных. И, наконец, PL/R. Как уже было сказано выше, это процедурный обработчик языка R для PostgreSQL, позволяющий писать SQL-функции на R.
Итак, в чем же преимущества PL/R? Во-первых, PL/R способствует развитию человеческих знаний и навыков, так как математика, статистика, базы данных и веб – это разные специализации, но все их придётся в той или иной мере освоить для работы с PL/R. Во-вторых, это расширение стимулирует улучшение “железа”, поскольку вам потребуется сервер, способный выдержать анализ больших наборов данных. В-третьих, вырастет эффективность обработки, так как вам больше не придется передавать большие наборы данных через всю сеть, и пропускная способность увеличится. В-четвертых, вы можете быть уверены, что анализ будет проводиться последовательно. В-пятых, PL/R делает систему любой сложности понятной и поддерживаемой. И, наконец, благодаря богатой функциональности и огромной экосистеме PL/R расширяет возможности R.
Но, конечно же, есть и минусы. Пользователю PostgreSQL скорее всего покажется, что PL/R работает медленнее, особенно на простых задачах. А для программиста на R усложнится процесс отладки и анализ станет менее гибким. Кроме того, обоим придётся учить новый язык.
Примерно вот так выглядит стандартная функция в R:
Создание функций в PL/R несколько отличается, но схоже с другими PL в PostgreSQL:
Приведем пример:
Сложно перечислить всё, что можно делать с помощью PL/R, но давайте подробно остановимся на некоторых важных свойствах, таких как:
Благодаря совместимости с PostgreSQL, мы можем создавать прототипы с помощью R, а затем перемещаться в PL/R для выполнения в “продакшене”. Также несомненным плюсом является то, что все запросы выполняются в текущей базе данных. Параметры настроек драйвера и подключения игнорируются, поэтому dbDriver, dbConnect, dbDisconnect и dbUnloadDriver не требуют затраты дополнительных усилий:
Давайте приведем пару примеров для наглядности. Допустим, нам нужно обратиться к PostgreSQL из R для решения знаменитой задачи коммивояжёра, которую позже мы рассмотрим подробно:
А вот так выглядит та же функция в PL/R:
Вот что нам в итоге выводит R:
И та же функция в PL/R:
Как вы видите, результат одинаковый.
Теперь поговорим об агрегатах (aggregates). Одним из самых полезных свойств PostgreSQL является возможность писать свои собственные агрегатные функции. Агрегаты в PostgreSQL можно расширять с помощью команд SQL. При этом указывается функция перехода между состояниями (state transition function) и, иногда, финальная функция (final function). Начальное условие функции перехода также может быть задано. И этими преимуществами вы можете пользоваться, работая с PL/R.
Приведем пример функции PL/R, реализующей новый агрегат. До недавнего времени это было невозможно сделать из PostgreSQL, функциональность GROUPING SETS появилась только в версии 9.5, в то время как PL/R позволяет делать это в любых версиях PG. Я создам агрегатную функцию на основе реальных данных одной производственной компании и назову её quartile:
R позволяет выводить данные в виде симпатичных графиков. В данном случае была использована коробчатая диаграмма:
По графику видно, что одна из производственных станций менее продуктивна по сравнению с остальными, и нужно принять меры, чтобы это исправить.
Отдельно стоит остановиться на оконных функциях (window functions). Они доступны в PostgreSQL, начиная с версии 8.4, и отлично подходят для статистического анализа. Оконные функции схожи с агрегатными, но, в отличие от них, не группируют строки, а позволяют производить расчеты в наборах строк, связанных с текущей строкой, имея доступ не только к текущей строке результата запроса. Иными словами, ваши данные разбиты на секции, и есть окно, которое скользит по этим секциям и выдаёт результат для каждой группы данных:
Немногие процедурные языки PostgreSQL поддерживают оконные функции, но в PL/R они весьма полезны. Приведем пример: создадим таблицу случайных данных, симулирующую доходы и цены на акции.
И напишем функцию для того чтобы выяснить, можно ли предсказать доходы в этом году, основываясь на показателях прошлого года, методом простой регрессии.
Как вы видите, функция посчитала нам зависимость доходов от показателей прошлых лет.
Последнее, о чем стоит поговорить подробно, это механизмы возврата объектов R и способы их хранения.
Приведем пример с биржевыми данными. Для этого возьмем Hi-Low-Close данные из Yahoo для любого “тикера” (stock ticker). Построим график с линиями Боллинджера и объёмом. Нам потребуются дополнительные R пакеты, которые можно получить из R следующей командой:
Теперь составим запрос:
Для типового сервера потребуе��ся экранный буфер, чтобы создать график:
Теперь вызовем функцию из PHP для тикера CYMI:
И вот такой график мы получаем на выходе:
Согласитесь, удивительно, что мы можем написать десяток строк на PL/R и меньше дюжины строк в PHP, а в итоге получить такое подробное визуальное отображение и анализ наших данных.
Чтобы закрепить информацию, рассмотрим более сложные примеры. Думаю, многие знакомы с законом Бенфорда, или законом первой цифры, который описывает вероятность появления определённой первой значащей цифры в распределениях величин, взятых из реальной жизни. Но некоторые не знают о его существовании и сами распределяют данные так, как им нужно, вместо того, чтобы применить закон.
Закон Бенфорда можно использовать для выявления потенциального мошенничества: с его помощью можно построить примерную геометрическую последовательность на основании нескольких начальных значений, а потом сравнить с реальными данными и найти несоответствия. Такой метод можно применять к графикам продаж, данным переписи, отчетам о затратах и т.д.
Рассмотрим пример с данными Калифорнийской программы по оптимизации энергозатрат. Для начала создадим и заполним таблицу с данными об инвестициях в проект (данные доступны по ссылке http://open-emv.com/data):
Теперь напишем функцию закона Бенфорда:
И запустим сравнение:
Похоже, что реальные данные соответствуют прогнозируемым, так что признаки мошенничества в данном случае отсутствуют.
Вернемся к задаче коммивояжёра. Это одна из самых известных задач комбинаторной оптимизации, заключающаяся в поиске самого выгодного маршрута, проходящего хотя бы раз через указанные города, с последующим возвратом в исходный город. В условиях задачи указываются критерии выгодности маршрута (кратчайший, наиболее дешёвый, совокупный критерий и так далее) и соответствующие матрицы расстояний, стоимости и тому подобного. Как правило, указывается, что маршрут должен проходить через каждый город только один раз. Давайте рассмотрим именно этот вариант.
Для начала создадим и наполним таблицу со всеми городами, которые нужно посетить:
Чтобы получить результат, мне придется написать пару вспомогательных запросов. Первый создаст маршрут, который я хочу получить на выходе:
А второй – данные, которые я ввожу в plr_modules, и тип итоговых данных:
Создадим основную функцию PL/R:
Теперь нам нужно установить функцию make.route():
И функцию make.map():
Запускаем функцию получения TSP метки:
Расширенный режим просмотра:
Таким образом, мы получили порядок, в котором стоит посещать эти города, расстояние между ними и т.д. Кроме того, у нас есть и наглядное решение задачи коммивояжёра:
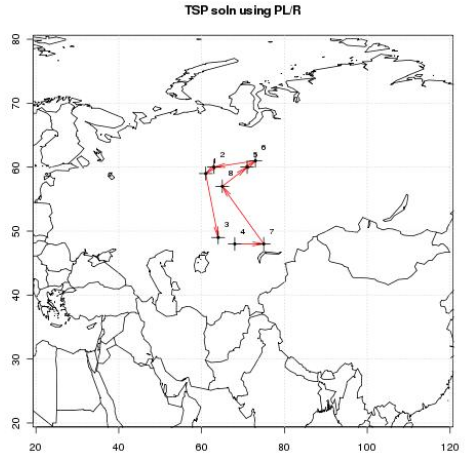
Рассмотрим еще один пример, на этот раз с сейсмическими данными.
Когда происходи�� землетрясение, оно обычно длится 15-20 секунд, и сейсмологи собирают данные об интенсивности его колебаний. То есть у нас есть временные ряды (timeseries) данных в формате осциллограммы (waveform data). Данные хранятся в виде массива чисел с плавающей запятой (floats), зарегистрированных во время сейсмического события с постоянной частотой выборки. Они доступны из онлайн-источников в отдельных файлах для каждой активности. В каждом файле находится около 16000 элементов.
Загрузим 1000 сейсмических активностей с помощью PL/pgSQL:
Это можно сделать и по-другому, с помощью R, и это займет в два раза меньше времени – тот редкий случай, когда использование PL/R ускоряет, а не замедляет процесс:
Создадим осцилограмму:
Получаем вот такую картинку для конкретного землетрясения:
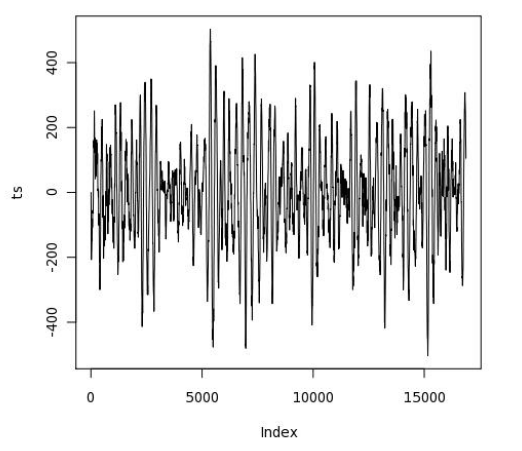
Теперь её нужно проанализировать, чтобы, например, узнать, как лучше проектировать здания в зоне с подобной сейсмической активностью. Вы наверняка помните из школьного курса физики такое понятие как «резонансная частота». На всякий случай напомню, что это такая частота колебаний, при которой амплитуда колебаний резко возрастает. Эта частота определяется свойствами системы. То есть в зоне с сейсмической активностью нужно проектировать строения таким образом, чтобы их резонансная частота не совпадала с частотой землетрясений. Это можно сделать с помощью R:
И вот так выглядит окончательный результат, показывающий частоту вибраций и их амплитуду:
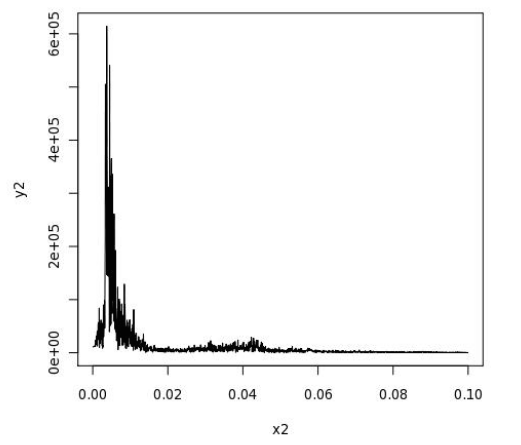
Имея такой график перед глазами, архитектор может сделать расчеты и спроектировать строение, которое не рухнет при первом же подземном толчке.
Как вы видите, у PL/R есть множество сфер применения, так как он позволяет связать продвинутую аналитику с базами данных и одновременно использовать функциональность R и PostgreSQL со всеми их преимуществами. Надеюсь, эта статья окажется вам полезна, и вы найдете применение столь эффективному и многофункциональному инструменту.
Приглашаем вас также ознакомиться с исходными материалами, на основе которых была подготовлена данная статья: презентация и видео с выступления Joe Conway на PG Day'15 Russia. Если тема применения PL/R кажется вам интересной, обязательно поделитесь своими соображениями и идеями. Кто знает, возможно, мы организуем доклад на эту тему на предстоящем PG Day'16 в июле. Как обычно, ждем ваших комментариев.

Последние тенденции в области Big Data поощряют сближение аналитики и данных, в то время как PL/R ненавязчиво предоставляет такой сервис вот уже 12 лет! Если вдруг вы не в курсе, PL/R – это расширение для PostgreSQL, позволяющее использовать R, язык для математических расчетов, прямо из PostgreSQL для того, чтобы легко и просто получать развернутую аналитику. Расширение доступно и активно совершенствуется с 2003 года. Оно работает со всеми поддерживаемыми версиями PostgreSQL и со всеми свежими версиями R. Тысячи людей во всем мире уже оценили его удобство и эффективность. Давайте же разберемся, что такое PL/R, обсудим достоинства и недостатки такого подхода к анализу данных и рассмотрим несколько примеров для наглядности.
Для начала дадим определения базовым понятиям. R – это язык программирования для статистической обработки данных и работы с графикой, а также свободная программная среда вычислений с открытым исходным кодом. А PostgreSQL – это мощная свободная объектно-реляционная система управления базами данных, которая активно разрабатывается вот уже более 25 лет и заработала отличную репутацию благодаря своей надежности, а также корректности и целостности данных. И, наконец, PL/R. Как уже было сказано выше, это процедурный обработчик языка R для PostgreSQL, позволяющий писать SQL-функции на R.
Итак, в чем же преимущества PL/R? Во-первых, PL/R способствует развитию человеческих знаний и навыков, так как математика, статистика, базы данных и веб – это разные специализации, но все их придётся в той или иной мере освоить для работы с PL/R. Во-вторых, это расширение стимулирует улучшение “железа”, поскольку вам потребуется сервер, способный выдержать анализ больших наборов данных. В-третьих, вырастет эффективность обработки, так как вам больше не придется передавать большие наборы данных через всю сеть, и пропускная способность увеличится. В-четвертых, вы можете быть уверены, что анализ будет проводиться последовательно. В-пятых, PL/R делает систему любой сложности понятной и поддерживаемой. И, наконец, благодаря богатой функциональности и огромной экосистеме PL/R расширяет возможности R.
Но, конечно же, есть и минусы. Пользователю PostgreSQL скорее всего покажется, что PL/R работает медленнее, особенно на простых задачах. А для программиста на R усложнится процесс отладки и анализ станет менее гибким. Кроме того, обоим придётся учить новый язык.
Примерно вот так выглядит стандартная функция в R:
func_name <- function(myarg1 [,myarg2...]) {
function body referencing myarg1 [, myarg2 ...]
}
Создание функций в PL/R несколько отличается, но схоже с другими PL в PostgreSQL:
CREATE OR REPLACE FUNCTION func_name(arg-type1 [, arg-type2 ...])
RETURNS return-type AS $$
function body referencing arg1 [, arg2 ...]
$$ LANGUAGE 'plr';
CREATE OR REPLACE FUNCTION func_name(myarg1 arg-type1 [, myarg2 arg-type2 ...])
RETURNS return-type AS $$
function body referencing myarg1 [, myarg2 ...]
$$ LANGUAGE 'plr';
Приведем пример:
CREATE EXTENSION plr;
CREATE OR REPLACE FUNCTION test_dtup(OUT f1 text, OUT f2 int)
RETURNS SETOF record AS $$
data.frame(letters[1:3],1:3)
$$ LANGUAGE 'plr';
SELECT * FROM test_dtup();
f1 | f2
----+----
a | 1
b | 2
c | 3
(3 rows)
Сложно перечислить всё, что можно делать с помощью PL/R, но давайте подробно остановимся на некоторых важных свойствах, таких как:
- совместимость с PostgreSQL;
- кастомные агрегаты SQL;
- оконные функции;
- перевод объекта R в bytea (двоичные строки).
Благодаря совместимости с PostgreSQL, мы можем создавать прототипы с помощью R, а затем перемещаться в PL/R для выполнения в “продакшене”. Также несомненным плюсом является то, что все запросы выполняются в текущей базе данных. Параметры настроек драйвера и подключения игнорируются, поэтому dbDriver, dbConnect, dbDisconnect и dbUnloadDriver не требуют затраты дополнительных усилий:
dbDriver(character dvr_name)
dbConnect(DBIDriver drv, character user, character password, character host, character dbname, character port, character tty, character options)
dbSendQuery(DBIConnection conn, character sql)
fetch(DBIResult rs, integer num_rows)
dbClearResult (DBIResult rs)
dbGetQuery(DBIConnection conn, character sql)
dbReadTable(DBIConnection conn, character name)
dbDisconnect(DBIConnection conn)
dbUnloadDriver(DBIDriver drv)
Давайте приведем пару примеров для наглядности. Допустим, нам нужно обратиться к PostgreSQL из R для решения знаменитой задачи коммивояжёра, которую позже мы рассмотрим подробно:
tsp_tour_length<-function() {
require(TSP)
require(fields)
require(RPostgreSQL)
drv <- dbDriver("PostgreSQL")
conn <- dbConnect(drv, user="postgres", dbname="plr", host="localhost")
sql.str <- "select id, st_x(location) as x, st_y(location) as y, location from stands"
waypts <- dbGetQuery(conn, sql.str)
dist.matrix <- rdist.earth(waypts[,2:3], R=3949.0)
rtsp <- TSP(dist.matrix)
soln <- solve_TSP(rtsp)
dbDisconnect(conn)
dbUnloadDriver(drv)
return(attributes(soln)$tour_length)
}
А вот так выглядит та же функция в PL/R:
CREATE OR REPLACE FUNCTION tsp_tour_length()
RETURNS float8 AS $$
require(TSP)
require(fields)
require(RPostgreSQL)
drv <- dbDriver("PostgreSQL")
conn <- dbConnect(drv, user="postgres", dbname="plr", host="localhost")
sql.str <- "select id, st_x(location) as x, st_y(location) as y, location from stands"
waypts <- dbGetQuery(conn, sql.str)
dist.matrix <- rdist.earth(waypts[,2:3], R=3949.0)
rtsp <- TSP(dist.matrix)
soln <- solve_TSP(rtsp)
dbDisconnect(conn)
dbUnloadDriver(drv)
return(attributes(soln)$tour_length)
$$ LANGUAGE 'plr' STRICT;
Вот что нам в итоге выводит R:
tsp_tour_length()
[1] 2804.581
И та же функция в PL/R:
SELECT tsp_tour_length();
tsp_tour_length
------------------
2804.58129355858
(1 row)
Как вы видите, результат одинаковый.
Теперь поговорим об агрегатах (aggregates). Одним из самых полезных свойств PostgreSQL является возможность писать свои собственные агрегатные функции. Агрегаты в PostgreSQL можно расширять с помощью команд SQL. При этом указывается функция перехода между состояниями (state transition function) и, иногда, финальная функция (final function). Начальное условие функции перехода также может быть задано. И этими преимуществами вы можете пользоваться, работая с PL/R.
Приведем пример функции PL/R, реализующей новый агрегат. До недавнего времени это было невозможно сделать из PostgreSQL, функциональность GROUPING SETS появилась только в версии 9.5, в то время как PL/R позволяет делать это в любых версиях PG. Я создам агрегатную функцию на основе реальных данных одной производственной компании и назову её quartile:
CREATE OR REPLACE FUNCTION r_quartile(ANYARRAY)
RETURNS ANYARRAY AS $$
quantile(arg1, probs = seq(0, 1, 0.25), names = FALSE)
$$ LANGUAGE 'plr';
CREATE AGGREGATE quartile (ANYELEMENT) (
sfunc = array_append,
stype = ANYARRAY,
finalfunc = r_quantile,
initcond = '{}'
);
SELECT workstation, quartile(id_val)
FROM sample_numeric_data
WHERE ia_id = 'G121XB8A' GROUP BY workstation;
workstation | quantile
-------------+---------------------------------
1055 | {4.19,5.02,5.21,5.5,6.89}
1051 | {3.89,4.66,4.825,5.2675,5.47}
1068 | {4.33,5.2625,5.455,5.5275,6.01}
1070 | {4.51,5.1975,5.485,5.7575,6.41}
(4 rows)
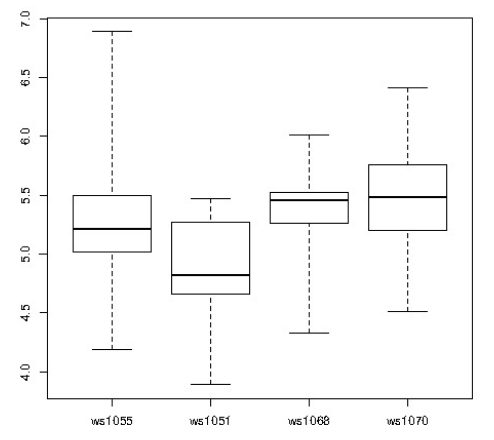
R позволяет выводить данные в виде симпатичных графиков. В данном случае была использована коробчатая диаграмма:

По графику видно, что одна из производственных станций менее продуктивна по сравнению с остальными, и нужно принять меры, чтобы это исправить.
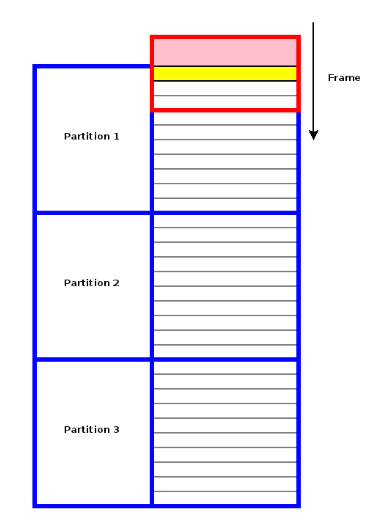
Отдельно стоит остановиться на оконных функциях (window functions). Они доступны в PostgreSQL, начиная с версии 8.4, и отлично подходят для статистического анализа. Оконные функции схожи с агрегатными, но, в отличие от них, не группируют строки, а позволяют производить расчеты в наборах строк, связанных с текущей строкой, имея доступ не только к текущей строке результата запроса. Иными словами, ваши данные разбиты на секции, и есть окно, которое скользит по этим секциям и выдаёт результат для каждой группы данных:

Немногие процедурные языки PostgreSQL поддерживают оконные функции, но в PL/R они весьма полезны. Приведем пример: создадим таблицу случайных данных, симулирующую доходы и цены на акции.
CREATE TABLE test_data (
fyear integer,
firm float8,
eps float8
);
INSERT INTO test_data
SELECT (b.f + 1) % 10 + 2000 AS fyear,
floor((b.f+1)/10) + 50 AS firm,
f::float8/100 + random()/10 AS eps
FROM generate_series(-500,499,1) b(f);
CREATE OR REPLACE FUNCTION r_regr_slope(float8, float8)
RETURNS float8 AS
$BODY$
slope <- NA
y <- farg1
x <- farg2
if (fnumrows==9) try (slope <- lm(y ~ x)$coefficients[2])
return(slope)
$BODY$ LANGUAGE plr WINDOW;
И напишем функцию для того чтобы выяснить, можно ли предсказать доходы в этом году, основываясь на показателях прошлого года, методом простой регрессии.
SELECT *, r_regr_slope(eps, lag_eps) OVER w AS slope_R
FROM (
SELECT firm AS f,
fyear AS fyr,
eps,
lag(eps) OVER (PARTITION BY firm ORDER BY firm, fyear) AS lag_eps
FROM test_data
) AS a
WHERE eps IS NOT NULL
WINDOW w AS (PARTITION BY firm ORDER BY firm, fyear ROWS 8 PRECEDING);
f | fyr | eps | lag_eps | slope_r
---+------+-------------------+-------------------+-------------------
1 | 1991 | -4.99563754182309 | |
1 | 1992 | -4.96425441872329 | -4.99563754182309 |
1 | 1993 | -4.96906093481928 | -4.96425441872329 |
1 | 1994 | -4.92376988714561 | -4.96906093481928 |
1 | 1995 | -4.95884547665715 | -4.92376988714561 |
1 | 1996 | -4.93236254784279 | -4.95884547665715 |
1 | 1997 | -4.90775520844385 | -4.93236254784279 |
1 | 1998 | -4.92082695348188 | -4.90775520844385 |
1 | 1999 | -4.84991340579465 | -4.92082695348188 | 0.691850614092383
1 | 2000 | -4.86000917562284 | -4.84991340579465 | 0.700526929134053
Как вы видите, функция посчитала нам зависимость доходов от показателей прошлых лет.
Последнее, о чем стоит поговорить подробно, это механизмы возврата объектов R и способы их хранения.
Приведем пример с биржевыми данными. Для этого возьмем Hi-Low-Close данные из Yahoo для любого “тикера” (stock ticker). Построим график с линиями Боллинджера и объёмом. Нам потребуются дополнительные R пакеты, которые можно получить из R следующей командой:
install.packages(c('xts','Defaults','quantmod','cairoDevice','RGtk2'))
Теперь составим запрос:
CREATE OR REPLACE FUNCTION plot_stock_data(sym text)
RETURNS bytea AS
$$
library(quantmod)
library(cairoDevice)
library(RGtk2)
pixmap <- gdkPixmapNew(w=500, h=500, depth=24)
asCairoDevice(pixmap)
getSymbols(c(sym))
chartSeries(get(sym), name=sym, theme="white", TA="addVo();addBBands();addCCI()")
plot_pixbuf <- gdkPixbufGetFromDrawable(NULL, pixmap,
pixmap$getColormap(),0, 0, 0, 0, 500, 500)
buffer <- gdkPixbufSaveToBufferv(plot_pixbuf, "jpeg", character(0), character(0))$buffer
return(buffer)
$$ LANGUAGE plr;
Для типового сервера потребуе��ся экранный буфер, чтобы создать график:
Xvfb :1 -screen 0 1024x768x24
export DISPLAY=:1.0
Теперь вызовем функцию из PHP для тикера CYMI:
<?php
$dbconn = pg_connect("...");
$rs = pg_query($dbconn, "select plr_get_raw(plot_stock_data('CYMI'))");
$hexpic = pg_fetch_array($rs);
$cleandata = pg_unescape_bytea($hexpic[0]);
header("Content-Type: image/png");
header("Last-Modified: " . date("r", filectime($_SERVER['SCRIPT_FILENAME'])));
header("Content-Length: " . strlen($cleandata));
echo $cleandata;
?>
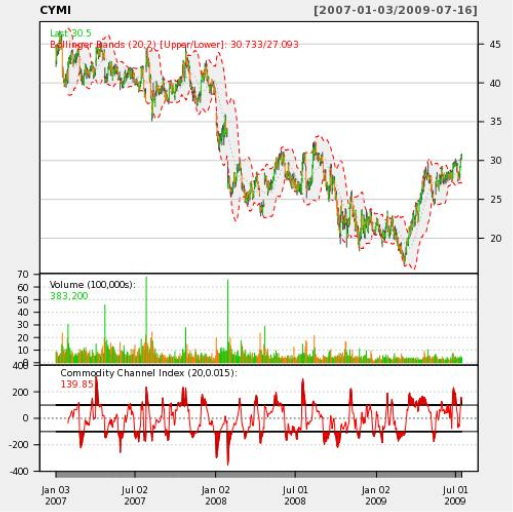
И вот такой график мы получаем на выходе:

Согласитесь, удивительно, что мы можем написать десяток строк на PL/R и меньше дюжины строк в PHP, а в итоге получить такое подробное визуальное отображение и анализ наших данных.
Чтобы закрепить информацию, рассмотрим более сложные примеры. Думаю, многие знакомы с законом Бенфорда, или законом первой цифры, который описывает вероятность появления определённой первой значащей цифры в распределениях величин, взятых из реальной жизни. Но некоторые не знают о его существовании и сами распределяют данные так, как им нужно, вместо того, чтобы применить закон.
Закон Бенфорда можно использовать для выявления потенциального мошенничества: с его помощью можно построить примерную геометрическую последовательность на основании нескольких начальных значений, а потом сравнить с реальными данными и найти несоответствия. Такой метод можно применять к графикам продаж, данным переписи, отчетам о затратах и т.д.
Рассмотрим пример с данными Калифорнийской программы по оптимизации энергозатрат. Для начала создадим и заполним таблицу с данными об инвестициях в проект (данные доступны по ссылке http://open-emv.com/data):
CREATE TABLE open_emv_cost(value float8, district int);
COPY open_emv_cost FROM 'open-emv.cost.csv' WITH delimiter ',';
Теперь напишем функцию закона Бенфорда:
CREATE TYPE benford_t AS (
actual_mean float8,
n int,
expected_mean float8,
distorion float8,
z float8
);
CREATE OR REPLACE FUNCTION benford(numarr float8[])
RETURNS benford_t AS
$$
xcoll <- function(x) {
return ((10 * x) / (10 ^ (trunc(log10(x)))))
}
numarr <- numarr[numarr >= 10]
numarr <- xcoll(numarr)
actual_mean <- mean(numarr)
n <- length(numarr)
expected_mean <- (90 / (n * (10 ^ (1/n) - 1)))
distorion <- ((actual_mean - expected_mean) / expected_mean)
z <- (distorion / sd(numarr))
retval <- data.frame(actual_mean,n,expected_mean,distorion,z)
return(retval)
$$ LANGUAGE plr;
И запустим сравнение:
SELECT * FROM benford(array(SELECT value FROM open_emv_cost));
-[ RECORD 1 ]-+----------------------
actual_mean | 38.1936561918275
n | 240
expected_mean | 38.8993031865999
distorion | -0.0181403505195804
z | -0.000984036908080443
Похоже, что реальные данные соответствуют прогнозируемым, так что признаки мошенничества в данном случае отсутствуют.
Вернемся к задаче коммивояжёра. Это одна из самых известных задач комбинаторной оптимизации, заключающаяся в поиске самого выгодного маршрута, проходящего хотя бы раз через указанные города, с последующим возвратом в исходный город. В условиях задачи указываются критерии выгодности маршрута (кратчайший, наиболее дешёвый, совокупный критерий и так далее) и соответствующие матрицы расстояний, стоимости и тому подобного. Как правило, указывается, что маршрут должен проходить через каждый город только один раз. Давайте рассмотрим именно этот вариант.
Для начала создадим и наполним таблицу со всеми городами, которые нужно посетить:
CREATE TABLE stands (
id serial primary key,
strata integer not null,
initage integer
);
SELECT AddGeometryColumn('','stands','boundary','4326','MULTIPOLYGON',2);
CREATE INDEX "stands_boundary_gist" ON "stands" USING gist ("boundary" gist_geometry_ops);
SELECT AddGeometryColumn('','stands','location','4326','POINT',2);
CREATE INDEX "stands_location_gist" ON "stands" USING gist ("location" gist_geometry_ops);
INSERT INTO stands (id,strata,initage,boundary,location)
VALUES
(
1,1,1,
GeometryFromText(
'MULTIPOLYGON(((59.250000 65.000000,55.000000 65.000000,55.000000 51.750000,
60.735294 53.470588, 62.875000 57.750000, 59.250000 65.000000 )))', 4326
),
GeometryFromText('POINT( 61.000000 59.000000 )', 4326)
), (
2,2,1,
GeometryFromText(
'MULTIPOLYGON(((67.000000 65.000000,59.250000 65.000000,62.875000 57.750000,
67.000000 60.500000, 67.000000 65.000000 )))', 4326
),
GeometryFromText('POINT( 63.000000 60.000000 )', 4326 )
), (
3,3,1,
GeometryFromText(
'MULTIPOLYGON(((67.045455 52.681818,60.735294 53.470588,55.000000 51.750000,
55.000000 45.000000, 65.125000 45.000000, 67.045455 52.681818 )))', 4326
),
GeometryFromText('POINT( 64.000000 49.000000 )', 4326 )
)
;
Чтобы получить результат, мне придется написать пару вспомогательных запросов. Первый создаст маршрут, который я хочу получить на выходе:
INSERT INTO stands (id,strata,initage,boundary,location)
VALUES
(
4,4,1,
GeometryFromText(
'MULTIPOLYGON(((71.500000 53.500000,70.357143 53.785714,67.045455 52.681818,
65.125000 45.000000, 71.500000 45.000000, 71.500000 53.500000 )))', 4326
),
GeometryFromText('POINT( 68.000000 48.000000 )', 4326)
), (
5,5,1,
GeometryFromText(
'MULTIPOLYGON(((69.750000 65.000000,67.000000 65.000000,67.000000 60.500000,
70.357143 53.785714, 71.500000 53.500000, 74.928571 54.642857, 69.750000 65.000000 )))', 4326
),
GeometryFromText('POINT( 71.000000 60.000000 )', 4326)
), (
6,6,1,
GeometryFromText(
'MULTIPOLYGON(((80.000000 65.000000,69.750000 65.000000,74.928571 54.642857,
80.000000 55.423077, 80.000000 65.000000 )))', 4326
),
GeometryFromText('POINT( 73.000000 61.000000 )', 4326)
), (
7,7,1,
GeometryFromText(
'MULTIPOLYGON(((80.000000 55.423077,74.928571 54.642857,71.500000 53.500000,
71.500000 45.000000, 80.000000 45.000000, 80.000000 55.423077 )))', 4326
),
GeometryFromText('POINT( 75.000000 48.000000 )', 4326)
), (
8,8,1,
GeometryFromText(
'MULTIPOLYGON(((67.000000 60.500000,62.875000 57.750000,60.735294 53.470588,
67.045455 52.681818, 70.357143 53.785714, 67.000000 60.500000 )))', 4326
),
GeometryFromText('POINT( 65.000000 57.000000 )', 4326)
)
;
А второй – данные, которые я ввожу в plr_modules, и тип итоговых данных:
DROP TABLE IF EXISTS events CASCADE;
CREATE TABLE events
(
seqid int not null primary key, -- visit sequence #
plotid int, -- original plot id
bearing real, -- bearing to next waypoint
distance real, -- distance to next waypoint
velocity real, -- velocity of travel, in nm/hr
traveltime real, -- travel time to next event
loitertime real, -- how long to hang out
totaltraveldist real, -- cummulative distance
totaltraveltime real -- cummulaative time
);
SELECT AddGeometryColumn('','events','location','4326','POINT',2);
CREATE INDEX "events_location_gist" ON "events" USING gist ("location" gist_geometry_ops);
CREATE TABLE plr_modules (
modseq int4 primary key,
modsrc text
);
Создадим основную функцию PL/R:
CREATE OR REPLACE FUNCTION solve_tsp(makemap bool, mapname text)
RETURNS SETOF events AS
$$
require(TSP)
require(fields)
sql.str <- "select id, st_x(location) as x, st_y(location) as y, location from stands;"
waypts <- pg.spi.exec(sql.str)
dist.matrix <- rdist.earth(waypts[,2:3], R=3949.0)
rtsp <- TSP(dist.matrix)
soln <- solve_TSP(rtsp)
tour <- as.vector(soln)
pg.thrownotice( paste("tour.dist=", attributes(soln)$tour_length))
route <- make.route(tour, waypts, dist.matrix)
if (makemap) {
make.map(tour, waypts, mapname)
}
return(route)
$$
LANGUAGE 'plr' STRICT;
Теперь нам нужно установить функцию make.route():
INSERT INTO plr_modules VALUES (
0,
$$ make.route <-function(tour, waypts, dist.matrix) {
velocity <- 500.0
starts <- tour[1:(length(tour))-1]
stops <- tour[2:(length(tour))]
dist.vect <- diag( as.matrix( dist.matrix )[starts,stops] )
last.leg <- as.matrix( dist.matrix )[tour[length(tour)],tour[1]]
dist.vect <- c(dist.vect, last.leg )
delta.x <- diff( waypts[tour,]$x )
delta.y <- diff( waypts[tour,]$y )
bearings <- atan( delta.x/delta.y ) * 180 / pi
bearings <- c(bearings,0)
for( i in 1:(length(tour)-1) ) {
if( delta.x[i] > 0.0 && delta.y[i] > 0.0 ) bearings[i] <- bearings[i]
if( delta.x[i] > 0.0 && delta.y[i] < 0.0 ) bearings[i] <- 180.0 + bearings[i]
if( delta.x[i] < 0.0 && delta.y[i] > 0.0 ) bearings[i] <- 360.0 + bearings[i]
if( delta.x[i] < 0.0 && delta.y[i] < 0.0 ) bearings[i] <- 180 + bearings[i]
}
route <- data.frame(seq=1:length(tour), ptid=tour, bearing=bearings, dist.vect=dist.vect,
velocity=velocity, travel.time=dist.vect/velocity, loiter.time=0.5)
route$total.travel.dist <- cumsum(route$dist.vect)
route$total.travel.time <- cumsum(route$travel.time+route$loiter.time)
route$location <- waypts[tour,]$location
return(route)}$$
);
И функцию make.map():
INSERT INTO plr_modules VALUES (
1,
$$make.map <-function(tour, waypts, mapname) {
require(maps)
jpeg(file=mapname, width = 480, height = 480, pointsize = 10, quality = 75)
map('world2', xlim = c(20, 120), ylim=c(20,80) )
map.axes()
grid()
arrows(
waypts[tour[1:(length(tour)-1)],]$x,
waypts[tour[1:(length(tour)-1)],]$y,
waypts[tour[2:(length(tour))],]$x,
waypts[tour[2:(length(tour))],]$y,
angle=10, lwd=1, length=.15, col="red"
)
points( waypts$x, waypts$y, pch=3, cex=2 )
points( waypts$x, waypts$y, pch=20, cex=0.8 )
text( waypts$x+2, waypts$y+2, as.character( waypts$id ), cex=0.8 )
title( "TSP soln using PL/R" )
dev.off()
}$$
);
Запускаем функцию получения TSP метки:
-- only needed if INSERT INTO plr_modules was in same session
SELECT reload_plr_modules();
SELECT seqid, plotid, bearing, distance, velocity, traveltime, loitertime, totaltraveldist
FROM solve_tsp(true, 'tsp.jpg');
NOTICE: tour.dist= 2804.58129355858
seqid | plotid | bearing | distance | velocity | traveltime | loitertime | totaltraveldist
-------+--------+---------+----------+----------+------------+------------+-----------------
1 | 8 | 131.987 | 747.219 | 500 | 1.49444 | 0.5 | 747.219
2 | 7 | -90 | 322.719 | 500 | 0.645437 | 0.5 | 1069.94
3 | 4 | 284.036 | 195.219 | 500 | 0.390438 | 0.5 | 1265.16
4 | 3 | 343.301 | 699.683 | 500 | 1.39937 | 0.5 | 1964.84
5 | 1 | 63.4349 | 98.2015 | 500 | 0.196403 | 0.5 | 2063.04
6 | 2 | 84.2894 | 345.957 | 500 | 0.691915 | 0.5 | 2409
7 | 6 | 243.435 | 96.7281 | 500 | 0.193456 | 0.5 | 2505.73
8 | 5 | 0 | 298.855 | 500 | 0.59771 | 0.5 | 2804.58
(8 rows)
Расширенный режим просмотра:
\x
SELECT * FROM solve_tsp(true, 'tsp.jpg');
NOTICE: tour.dist= 2804.58129355858
-[ RECORD 1 ]---+---------------------------------------------------
seqid | 1
plotid | 3
bearing | 104.036
distance | 195.219
velocity | 500
traveltime | 0.390438
loitertime | 0.5
totaltraveldist | 195.219
totaltraveltime | 0.890438
location | 0101000020E610000000000000000050400000000000804840
-[ RECORD 2 ]---+---------------------------------------------------
[...]
Таким образом, мы получили порядок, в котором стоит посещать эти города, расстояние между ними и т.д. Кроме того, у нас есть и наглядное решение задачи коммивояжёра:

Рассмотрим еще один пример, на этот раз с сейсмическими данными.
Когда происходи�� землетрясение, оно обычно длится 15-20 секунд, и сейсмологи собирают данные об интенсивности его колебаний. То есть у нас есть временные ряды (timeseries) данных в формате осциллограммы (waveform data). Данные хранятся в виде массива чисел с плавающей запятой (floats), зарегистрированных во время сейсмического события с постоянной частотой выборки. Они доступны из онлайн-источников в отдельных файлах для каждой активности. В каждом файле находится около 16000 элементов.
Загрузим 1000 сейсмических активностей с помощью PL/pgSQL:
DROP TABLE IF EXISTS test_ts;
CREATE TABLE test_ts (
dataid bigint NOT NULL PRIMARY KEY,
data double precision[]
);
CREATE OR REPLACE FUNCTION load_test(int)
RETURNS text AS
$$
DECLARE
i int;
arr text;
sql text;
BEGIN
arr := pg_read_file('array-data.csv', 0, 500000);
FOR i IN 1..$1 LOOP
sql := $i$INSERT INTO test_ts(dataid,data) VALUES ($i$ || i || $i$,'{$i$ || arr || $i$}')$i$;
EXECUTE sql;
END LOOP;
RETURN 'OK';
END;
$$ LANGUAGE plpgsql;
SELECT load_test(1000);
load_test
-----------
OK
(1 row)
Time: 37336.539 ms
Это можно сделать и по-другому, с помощью R, и это займет в два раза меньше времени – тот редкий случай, когда использование PL/R ускоряет, а не замедляет процесс:
DROP TABLE IF EXISTS test_ts_obj;
CREATE TABLE test_ts_obj (
dataid serial PRIMARY KEY,
data bytea
);
CREATE OR REPLACE FUNCTION make_r_object(fname text)
RETURNS bytea AS
$$
myvar<-scan(fname,sep=",")
return(myvar);
$$ LANGUAGE 'plr' IMMUTABLE;
INSERT INTO test_ts_obj (data)
SELECT make_r_object('array-data.csv')
FROM generate_series(1,1000);
INSERT 0 1000
Time: 12166.137 ms
Создадим осцилограмму:
CREATE OR REPLACE FUNCTION plot_ts(ts double precision[])
RETURNS bytea AS
$$
library(quantmod)
library(cairoDevice)
library(RGtk2)
pixmap <- gdkPixmapNew(w=500, h=500, depth=24)
asCairoDevice(pixmap)
plot(ts,type="l")
plot_pixbuf <- gdkPixbufGetFromDrawable(
NULL, pixmap, pixmap$getColormap(), 0, 0, 0, 0, 500, 500
)
buffer <- gdkPixbufSaveToBufferv(
plot_pixbuf,
"jpeg",
character(0),
character(0)
)$buffer
return(buffer)
$$ LANGUAGE 'plr' IMMUTABLE;
SELECT plr_get_raw(plot_ts(data)) FROM test_ts WHERE dataid = 42;
Получаем вот такую картинку для конкретного землетрясения:

Теперь её нужно проанализировать, чтобы, например, узнать, как лучше проектировать здания в зоне с подобной сейсмической активностью. Вы наверняка помните из школьного курса физики такое понятие как «резонансная частота». На всякий случай напомню, что это такая частота колебаний, при которой амплитуда колебаний резко возрастает. Эта частота определяется свойствами системы. То есть в зоне с сейсмической активностью нужно проектировать строения таким образом, чтобы их резонансная частота не совпадала с частотой землетрясений. Это можно сделать с помощью R:
CREATE OR REPLACE FUNCTION plot_fftps(ts bytea)
RETURNS bytea AS
$$
library(quantmod)
library(cairoDevice)
library(RGtk2)
fourier<-fft(ts)
magnitude<-Mod(fourier)
y2 <- magnitude[1:(length(magnitude)/10)]
x2 <- 1:length(y2)/length(magnitude)
mydf <- data.frame(x2,y2)
pixmap <- gdkPixmapNew(w=500, h=500, depth=24)
asCairoDevice(pixmap)
plot(mydf,type="l")
plot_pixbuf <- gdkPixbufGetFromDrawable(
NULL, pixmap, pixmap$getColormap(), 0, 0, 0, 0, 500, 500
)
buffer <- gdkPixbufSaveToBufferv(
plot_pixbuf, "jpeg", character(0), character(0)
)$buffer
return(buffer)
$$ LANGUAGE 'plr' IMMUTABLE;
SELECT plr_get_raw(plot_fftps(data)) FROM test_ts_obj WHERE dataid = 42;
И вот так выглядит окончательный результат, показывающий частоту вибраций и их амплитуду:

Имея такой график перед глазами, архитектор может сделать расчеты и спроектировать строение, которое не рухнет при первом же подземном толчке.
Как вы видите, у PL/R есть множество сфер применения, так как он позволяет связать продвинутую аналитику с базами данных и одновременно использовать функциональность R и PostgreSQL со всеми их преимуществами. Надеюсь, эта статья окажется вам полезна, и вы найдете применение столь эффективному и многофункциональному инструменту.
Приглашаем вас также ознакомиться с исходными материалами, на основе которых была подготовлена данная статья: презентация и видео с выступления Joe Conway на PG Day'15 Russia. Если тема применения PL/R кажется вам интересной, обязательно поделитесь своими соображениями и идеями. Кто знает, возможно, мы организуем доклад на эту тему на предстоящем PG Day'16 в июле. Как обычно, ждем ваших комментариев.