Хабр Курсы для всех
РЕКЛАМА
Практикум, Хекслет, SkyPro, авторские курсы — собрали всех и попросили скидки. Осталось выбрать!
Хабр доступен 24/7 благодаря поддержке друзей
Комментарии 386
Определенный интеграл от функции — есть площадь — не проще было ли найти площадь четверти круга?
Наверное именно простейшего решения от Вас и добивались?
Наверное именно простейшего решения от Вас и добивались?
Не совсем вас понял.
Площадь какого круга вы имеете в виду?
Может я и правда пропустил простейшее решение?
Площадь какого круга вы имеете в виду?
Может я и правда пропустил простейшее решение?
Перейдите в полярные координаты, например.
Интеграл в полярных координатах не равен площади.
Да, верно. Требуется преобразование кординат х и у в р и ф. Просто я предположил, что может упроститься формула. Однако, я ошибся, навскидку кривая получается вообще невообразимой. Во-первых надо сместиться на пи/2 с точкой отсчета, во-вторых дикие формулы с арктангенсами не дают надежды на ростое сокращение.
Тонкий вопрос связан с тем, что вы фактически все равно используете в промежуточных вычислениях (в выводе конечной формулы) косинус, когда вы говорите «я бы представил косинус как...»
Вы, конечно, можете его не упоминать и пропустить этот элемент в цепочке, но я не уверен, что про результат можно сказать, что он получен вообще без использования косинуса.
Вы, конечно, можете его не упоминать и пропустить этот элемент в цепочке, но я не уверен, что про результат можно сказать, что он получен вообще без использования косинуса.
Площадь круга с радиусом 1 равна Пи.
Другое дело что функция «четверти круга» и синус — это разные функции.
Другое дело что функция «четверти круга» и синус — это разные функции.
Представьте график функции sin(x) в интервале от нуля до пи – это будет полукруг. Вот его площадь – это и будет результат вычисления этого интеграла в этом промежутке.
Четверть круга вам мало поможет при нахождении интеграла от синуса.
deleted
Про площадь — хорошая подсказка. Круг тут не причем.
Нарисовать график (мы знаем несколько опорных точек) и посчитать «по клеточкам». Вполне приближенное значение получится
Нарисовать график (мы знаем несколько опорных точек) и посчитать «по клеточкам». Вполне приближенное значение получится
Читал, как заклинания…
Магия…
Магия…
Пора освежить знания, а то тоже больше половины ничего не понял (:
Я придумал новый способ собеседования. Даём каждому из кандидатов текст с математическими выкладками, где сложность материала постепенно растёт от начала к концу.
Побеждает тот кандидат, который, двигаясь от начала текста к концу, перестанет понимать о чём речь, позже других.
Отдельный вопрос: как проверить, где кандидат действительно понимает, а где уже нет.
Ответ: например пригласить какого-нибудь прожённого до мозга костей гуманитария и заставить кандидата объяснять материал ему, ведь как гласит известное высказывание: «если вы не можете объяснить что-то простым языком — вы этого не понимаете».
Побеждает тот кандидат, который, двигаясь от начала текста к концу, перестанет понимать о чём речь, позже других.
Отдельный вопрос: как проверить, где кандидат действительно понимает, а где уже нет.
Ответ: например пригласить какого-нибудь прожённого до мозга костей гуманитария и заставить кандидата объяснять материал ему, ведь как гласит известное высказывание: «если вы не можете объяснить что-то простым языком — вы этого не понимаете».
Где же столько свежих прожжённых гуманитариев найти?..
Суд по своему опыту собеседований могу сказать — есть действительно интересные собеседники, которые всю встречу проводят как обычный дружеский разговор, могут спокойно угостить тортиком и позвать разговаривать в бильярдную комнату. А есть му@#ки, которые приходят на собеседование «подвешивать», «вгонять в ступор» и всячески доказывать свое превосходство, крутизну и ошеломительное остроумие постороннему человеку. Как правило — следствие личной неудовлетворенности, либо же тошнотворное состояние в текущей организации. В общем, не заморачивайтесь, я бы не хотел работать с таким вот индивидуумом в одном помещении. Очень многие здесь будут смотреть на вас, как на бога математики. В том числе и я.
А рассказ, задачи и ход мышления интересный, заставил разрыть вику в разделе математики и взять в руки листик с ручкой. Спасибо.
А рассказ, задачи и ход мышления интересный, заставил разрыть вику в разделе математики и взять в руки листик с ручкой. Спасибо.
Странность еще в том, что мой собеседователь производил впечатление адекватного человека, совсем не муд… ка (как вы выразились). Часть его вопросов была абсолютно релевантна вакансии. То есть я не могу сказать, что он меня пытался однозначно «завалить».
Да и эти были вполне приемлемыми (за исключением того, что нельзя было пользоваться ручкой с бумагой).
Но вот как он интерпретировал мои ответы — это уже другой вопрос.
Да и эти были вполне приемлемыми (за исключением того, что нельзя было пользоваться ручкой с бумагой).
Но вот как он интерпретировал мои ответы — это уже другой вопрос.
Как видите, быть адекватным человеком и производить впечатление адекватного человека — совершенно разные вещи.
Да, забыл добавить. Проводя собеседования по программированию всегда предлагаю ручку-бумагу. Блок-схемы рисовать самое то. Но, честно говоря, попав на чисто математическое собеседование и услышав требование обойтись без ручки и бумаги я бы вежливо извинился и попрощался бы с товарищами, не раздумывая ни минуты. Математика — не тот предмет, в котором можно без последствий ткнуть пальцем в воздух и получить нужное решение.
Да, забыл добавить. Проводя собеседования по программированию всегда предлагаю ручку-бумагу. Блок-схемы рисовать самое то. Но, честно говоря, попав на чисто математическое собеседование и услышав требование обойтись без ручки и бумаги я бы вежливо извинился и попрощался бы с товарищами, не раздумывая ни минуты. Математика — не тот предмет, в котором можно без последствий ткнуть пальцем в воздух и получить нужное решение.
Можно ещё предположить, что искали кандидата с определённым складом мышления, чтобы потом можно было с ним общаться сразу на достаточно глубоком уровне обобщений, аналогий и умолчаний, не пробиваясь каждый раз через «аксиомы и определения». И «А» считал, что способность «вычислить интеграл синуса без косинуса», не пытаясь обмануть систему — или хотя бы порассуждать об этом — подходящий тестовый вопрос. Другой вопрос — найдут ли они кого-нибудь подходящего, а если найдут — смогут ли закончить хотя бы один проект, или будут радостно разрабатывать метаархитектуры исключительно на категорных принципах — и считать, что средства оправдывают цель :)
Вот, например, на одном из собеседований у меня спросили, в чём задача ORM. Я ответил — в конвертировании данных различного формата и их связей в нативные объекты языка программирования и обратно.
Оказывается, правильный ответ был — «задача ORM в предоставлении абстракции». Вот так, без дополнений и пояснений.
Оказывается, правильный ответ был — «задача ORM в предоставлении абстракции». Вот так, без дополнений и пояснений.
Согласен, такие мудаки не стоят того чтобы тратить свое время
>> есть му@#ки, которые приходят на собеседование «подвешивать», «вгонять в ступор» и всячески доказывать свое превосходство, крутизну и ошеломительное остроумие постороннему человеку.
Особенно круто, когда эти м%даки — нет, не твое будущее начальство. А твои будущие подчиненные. Которых не пойми с какой радости отправили тебя собеседовать, и которые со второй минуты разговора сразу говорят — «ну, будем тебя валить»(почти дословно). Нет, это не шутка была.
Особенно круто, когда эти м%даки — нет, не твое будущее начальство. А твои будущие подчиненные. Которых не пойми с какой радости отправили тебя собеседовать, и которые со второй минуты разговора сразу говорят — «ну, будем тебя валить»(почти дословно). Нет, это не шутка была.
Когда мне приходилось брать на работу экономистов, вероятно, часто я в их глазах выглядел этаким самодуром. Но, что поделаешь, когда требуемый уровень навыков и опыта кандидату даже приблизительно неизвестен?
Вполне возможно, что Вы просто не до конца поняли требования к вакансии и решили, что она Вам подходит, хотя она требует качественно другого уровня знаний.
А возможно произошел обычный личностный диссонанс. За Ваш счет попытались самоутвердиться.
Определить наличие необходимых аналитических способностей у кандидата можно точно лишь в двух случаях.
1. Известна необходимая методика анализа и требуется определенная степень владения методикой
2. Есть критерии оценки правильно проведенного анализа и требуется такой анализ продемонстрировать
Однако, есть ситуации, когда качество анализа проверить без серьезных затрат нельзя. Тогда все упирается в интуицию нанимателя и харизму нанимаемого
Вполне возможно, что Вы просто не до конца поняли требования к вакансии и решили, что она Вам подходит, хотя она требует качественно другого уровня знаний.
А возможно произошел обычный личностный диссонанс. За Ваш счет попытались самоутвердиться.
Определить наличие необходимых аналитических способностей у кандидата можно точно лишь в двух случаях.
1. Известна необходимая методика анализа и требуется определенная степень владения методикой
2. Есть критерии оценки правильно проведенного анализа и требуется такой анализ продемонстрировать
Однако, есть ситуации, когда качество анализа проверить без серьезных затрат нельзя. Тогда все упирается в интуицию нанимателя и харизму нанимаемого
Вариант с разложением на комплексные экспоненты — наверно, самый очевидный вариант, при запрете на косинус. В случае, если бы это не проканало, я бы предложил заменить функцию косинус по определению: отношение прилежащего катета к гипотенузе:)
Вопрос про pi = 3 на мой взгляд некорректный. Действительно, очевидно, что поменялось бы всё на свете.
а на вопрос про pi^2 = 10 я бы ответил, что в таком случае pi было бы равно корню из 10.
Вопрос про pi = 3 на мой взгляд некорректный. Действительно, очевидно, что поменялось бы всё на свете.
а на вопрос про pi^2 = 10 я бы ответил, что в таком случае pi было бы равно корню из 10.
а на вопрос про pi^2 = 10 я бы ответил, что в таком случае pi было бы равно корню из 10.
Во-первых, мне этот вопрос задан не был (это был комментарий от самого собеседователя).
Что он имел в виду — я точно не знаю.
Но я думаю, что не все так просто, как вы думаете, имелось в виду что-то другое.
Мне, просто, кажется, что на такие вопросы ждут не верного ответа, а чтобы вы быстро и уверенно смогли навешать им лапши на уши.
Вот вы попросили человека А уточнить его ограничение на косинус. Я думаю, тут надо было трактовать это на своё усмотрение. Генерировать побыстрее ответ. А потом, если он к чему-то — ответить, что нюансы, которые не были оговорены, вы трактовали на своё усмотрение и что ваш ответ никак не противоречит условию.
Вот вы попросили человека А уточнить его ограничение на косинус. Я думаю, тут надо было трактовать это на своё усмотрение. Генерировать побыстрее ответ. А потом, если он к чему-то — ответить, что нюансы, которые не были оговорены, вы трактовали на своё усмотрение и что ваш ответ никак не противоречит условию.
Если бы пи было равно трем я бы подумал о переходе в пи-ричную систему счисления. По крайней мере это вопрос либо самого числового поля, либо топологии пространства.
Но я бы точно не стал бы вспоминать о формулах, поскольку число пи выводится как отношение длины окружности к ее диаметру и все остальные применния лишь связаны с этим топологическим свойством отношения минимального периметра для максимальной площади к его проекции.
Но я бы точно не стал бы вспоминать о формулах, поскольку число пи выводится как отношение длины окружности к ее диаметру и все остальные применния лишь связаны с этим топологическим свойством отношения минимального периметра для максимальной площади к его проекции.
Нет, разговор о возможности изменения системы счисления, в которой бы Pi=3 не стоял. То есть банально принимаем число 3 за Pi.
Я это сразу предложил (забыл написать здесь).
Ваше же второе утверждение достаточно глубокое, конечно. Но оно не закончено. Требуется продолжить, что бы было дальше, какие св-ва были у того пр-ва, где отношение длины окружности (в определении того пространства) к ее диаметру было бы другим (3)? Что дальше? Если бы там как-то изменились физические законы, то как именно? Приведите пример.
Я это сразу предложил (забыл написать здесь).
Ваше же второе утверждение достаточно глубокое, конечно. Но оно не закончено. Требуется продолжить, что бы было дальше, какие св-ва были у того пр-ва, где отношение длины окружности (в определении того пространства) к ее диаметру было бы другим (3)? Что дальше? Если бы там как-то изменились физические законы, то как именно? Приведите пример.
Формально ничего не изменится, ведь топология это связанность, а не соотношения. Тот же периметр, та же площадь, только проекция будет не на прямую линию, а на что-то типа цепной линии. Таким образом получится, что весь мир как бы провисает во времени, время движется нелинейно, а так, что из любой точки оно выглядит самым быстрым прямо сейчас, все более удаленное будущее развивается медленнее, как и прошлое.
Получился бы такой парадокс застывшего времени, как в бесконечном прошлом, так и в бесконечном будущем.
В случае с пи как корнь из десяти цепная линия была бы чуть более пологой.
Это как если на доску нагрузить гири и они, ргибая доску скатываются ближе к ее центру.
Ничего более существенного, кроме математических казусов и трансформации значений физических констант с миром бы не случилось.
По сути это как смотреть на мир через искажающую линзу или зеркало. Меняется восприятие, но не мир.
Получился бы такой парадокс застывшего времени, как в бесконечном прошлом, так и в бесконечном будущем.
В случае с пи как корнь из десяти цепная линия была бы чуть более пологой.
Это как если на доску нагрузить гири и они, ргибая доску скатываются ближе к ее центру.
Ничего более существенного, кроме математических казусов и трансформации значений физических констант с миром бы не случилось.
По сути это как смотреть на мир через искажающую линзу или зеркало. Меняется восприятие, но не мир.
А не вышло бы так, что пространство с отношением периметра к диаметру равным трём оказалось бы очень выпуклым?
Тут-то и подкрадывается «Большой Пц» в виде «Большого схлопывания». А поскольку метрика уж очень чрезмерно выпукла, то БПц/БСхл наступит очень чрезмерно быстро. Типа через минут 5 после Большого взрыва.
Тут-то и подкрадывается «Большой Пц» в виде «Большого схлопывания». А поскольку метрика уж очень чрезмерно выпукла, то БПц/БСхл наступит очень чрезмерно быстро. Типа через минут 5 после Большого взрыва.
Ну тут действительно не совсем понятно, что именно подразумевается под запретом косинуса и насколько далеко эти запреты распространяются. В решении с экспонентами мы получаем, как верно заметил автор, тот же косинус, но записанный в виде формулы. Если так, то можно не городить огород, а просто в самом очевидном решении в первообразной использовать не -cos, а -sqrt(1-sin^2). По смыслу это то же самое, что косинус, замаскированный под экспоненты. А если и такой вариант запрещен, то можно довести задачу до абсурда, сказав, что тогда и синус оказывается автоматически запрещенным, так как выводится из этой формулы через косинус.
Вы прекрасный математический анти-демагог!
Но синус и есть форма косинуса.
(И наеборот)
(И наеборот)
В принципе, верно, можно было бы ответить, что вычислить предложенный интеграл от синуса совсем без применения косинуса не удастся, т.к. сам синус — это фактически сдвинутый на Pi/2 косинус.
Я об этом сразу даже не подумал, хотя это лежало на поверхности.
Но если верный ответ предусматривал именно это решение, то это сродни задачке «А и Б сидели на трубе».
Я об этом сразу даже не подумал, хотя это лежало на поверхности.
Но если верный ответ предусматривал именно это решение, то это сродни задачке «А и Б сидели на трубе».
Решение с экспонентами нельзя использовать, на мой взгляд. Как подсчитать exp(i*Pi)? Единственный известный мне способ — это через ту же формулу эйлера разложить ее на синус и косинус*i. Опять получаем косинус. Ну или в ряд раскладывать, но это ничем не лучше, чем разложить в ряд синус и проинтегрировать его. Или косинус считать через известный уже ряд.
Ну или в ряд раскладывать, но это ничем не лучше, чем разложить в ряд синус и проинтегрировать его. Или косинус считать через известный уже ряд
В том-то и проблема, что если разложить в ряд синус, а потом проинтегрировать, то получится ряд для минус косинуса, я об этом писал. Как вы будете еще считать без применения косинуса? Можете показать решение?
Решение с экспонентами нельзя использовать, на мой взгляд. Как подсчитать exp(i*Pi)?
Здесь вопрос, что именно имел в виду интервьюер. Может он хотел, чтобы в самом решении не использовалось написание cos нигде? Тогда такой вариант пройдет, т.к. мы полагаем exp(i*Pi)=-1 известным фактом и не проверяем, как он был получен.
P.S. А как бы вы сами стали решать это задачу?
Пока интервьювер не объяснит, что значит — не использовать косинус, никак. Задача из серии «сколько лампочек в аудитории?». И сиди думай, принес ли интервьювер свою лампочку, и сколько. Если без объяснения — то просто сказал бы, что ответ площадь под графиком. Любое численное значение посчитанное через какие-либо известные значения каких-либо функций рано или поздно упирается в значения первообразной от синуса, что и есть косинус.
Вот здесь
интересное решение без косинуса, посмотрите.
интересное решение без косинуса, посмотрите.
Не корню из 3, а плюс-минус корню из 3. Мне кажется, вариант с отрицательным пи подвнсил бы уже спросившего
Я бы ответил, что если бы число Pi равнялось 3, то длина окружности, равнялась бы, скажем 2LuR, где Lu — это 3.14…
В том смысле, что Pi — это всего лишь имя числа имеющего определённое значение и высчитывающегося определённым образом, а не наоборот.
В том смысле, что Pi — это всего лишь имя числа имеющего определённое значение и высчитывающегося определённым образом, а не наоборот.
Он некорректный не потому, что поменялось бы всё на свете, а потому что этого просто не может быть, как не может быть 2*2=5.
Да ну… а вас не смущает, что 2*8 в десятичной системе равно 16, а шестнадцатиричной 10. Это с одной стороны.
С другой же, можно представить себе «мир», где pi равно 3. Так же, как я могу себе представить что pi равно 3.14 или 3.14159. До какого знака после запятой вы обычно округляете пи? 3.14? Так я вам заявляю:
Ну или как в симпсонах, для привлечения внимания :).
С другой же, можно представить себе «мир», где pi равно 3. Так же, как я могу себе представить что pi равно 3.14 или 3.14159. До какого знака после запятой вы обычно округляете пи? 3.14? Так я вам заявляю:
это некорректно не потому, что поменялось бы всё на свете, а потому что этого просто не может быть, как не может быть 2*2=5Выражение пи равно 3, как правило означает всего лишь, что точностью в вычислении можно принебречь (я округлил до 0 знака). Всё.
Ну или как в симпсонах, для привлечения внимания :).
Почему не может? Я плоховато помню линейную алгебру, но вроде бы никто не запрещает создать свою конечную группу и на ней объявить умножение таким образом, чтобы 2*2 было равно 5.
а на вопрос про pi^2 = 10 я бы ответил, что в таком случае pi было бы равно корню из 10.Как скучно. Можно было бы предположить, что пи равно минус корню из десяти. И начать рассуждения а том, что получится с пространством, если пи будет отрицательным.
Может получилось бы «вогнать в ступор» собеседуещего.
Если вы таким образом искали ответ на риторический вопрос «почему человек A — говнюк?», то вы явно не по адресу. Также вы сами прекрасно понимаете, что подобными вопросами аналитический уровень человека проверить невозможно. Поэтому если в следующий раз вы попадете в аналогичную ситуацию — сэкономьте себе время и просто напишите в твиттере, что представитель компании X проводящий собеседование на позицию аналитика — говнюк. Нужно просто быть более толстокожим и не обижаться на ерунду.
Интересный случай, но более интересен ответ на вопрос про два шара:) Правда ли, что можно отвечать так: возьмём ограниченное метрическое пространство (например, сферу или поверхность тора), и выберем в нём два шара радиуса R_1 и R_2 большего, чем максимальное расстояние между точками в этом пространстве? Тогда эти шары совпадут (каждый заполнит всё пространство) и каждый будет лежать внутри другого. И есть ли более красивое решение?
Прикольное решение :)
Я, правда, забыл уточнить, что «внутри» означает то, что шары не должны совпадать друг с другом полностью как множества.
Я, правда, забыл уточнить, что «внутри» означает то, что шары не должны совпадать друг с другом полностью как множества.
Хорошо) Тогда возьмём в качестве пространства, ну, например, квадрат (с евклидовой метрикой). Первый шар имеет центр в вершине квадрата (и в этом пространстве представляет собой сектор), центр второго — на некотором небольшом расстоянии от него. Его радиус можно выбрать чуть меньше и он всё равно покроет весь сектор.
Отрезок [0,3]. Берем шар радиуса 3/2 с центром в точке 2 и шар радиуса 2 с центром в точке 3.
Минимальный пример, конечно, пространство из двух точек.
Минимальный пример, конечно, пространство из двух точек.
А не из трёх ли, если хочется именно строгое включение?
Да, верно, чтобы было строгое включение нужно три точки (насколько я помню). Достаточно построить шары на треугольнике со сторонами 3,4,5.
Точки нашего пр-ва — это вершины треугольника.
Первый шар — с центром с вершиной при прямом угле и радиусом 4.1 В этот шар войдут три точки.
Второй шар — в любой другой вершине и с радиусом 4.2. В этот шар войдут только две точки.
Метрика евклидова из R2
Точки нашего пр-ва — это вершины треугольника.
Первый шар — с центром с вершиной при прямом угле и радиусом 4.1 В этот шар войдут три точки.
Второй шар — в любой другой вершине и с радиусом 4.2. В этот шар войдут только две точки.
Метрика евклидова из R2
Да, три, глупость сказал. Можно взять точки 0, 1 и 2 на прямой c обычным расстоянием.
Ну а тогда для нестрогого включения минимальный пример вообще из одной точки.
Да, все верно, вроде. Пример получился еще проще, чем у меня.
Что мы имеем: очень простой пример для задачи, которая формулируется очень непривычно.
Хотя пример и выглядит предельно простым, мне кажется, все равно нужно определенное чутье или опыт, чтобы быстро такой пример придумать.
Грубо говоря, не каждый человек, которому дали определение метрического пр-ва, сразу сможет построить такой пример.
Мне кажется так. Может я ошибаюсь.
Что мы имеем: очень простой пример для задачи, которая формулируется очень непривычно.
Хотя пример и выглядит предельно простым, мне кажется, все равно нужно определенное чутье или опыт, чтобы быстро такой пример придумать.
Грубо говоря, не каждый человек, которому дали определение метрического пр-ва, сразу сможет построить такой пример.
Мне кажется так. Может я ошибаюсь.
Про шары. От меня до соседа 2 метра, но когда я отправляю сообщение ему и в ЦОД. Latency между мной и ЦОДом — 0,2. А latency я — ЦОД — сосед = 0,4.
Вы меня подвесили.
Погодите. Не совсем вас понял.
Вы фактически можете подразумевать две вещи под метрикой:
1. Метрика из R^3 (в метрах)
2. latency (в мс)
Это две разные метрики.
Какую из этих двух метрик вы используете, чтобы построить этот пример?
Не должно быть такого, что один шар вы считаете по одной метрике, а другой — по другой.
Вы фактически можете подразумевать две вещи под метрикой:
1. Метрика из R^3 (в метрах)
2. latency (в мс)
Это две разные метрики.
Какую из этих двух метрик вы используете, чтобы построить этот пример?
Не должно быть такого, что один шар вы считаете по одной метрике, а другой — по другой.
Да, вы правы. Я тут вырезал два круга из бумаги, скомкал большой и впрессовал его в маленький. То есть выполнил N+1-мерное преобразование в N-мерном пространстве.
Поясню. Я имел в виду, что я при времени 0,3 охватываю только две точки (включая себя), а ЦОД при времени 0,25 охватывает три точки (включая себя).
Директор по кадрам Гугла рассказал все, что нужно знать, вот в этой статье:
www.nytimes.com/2013/06/20/business/in-head-hunting-big-data-may-not-be-such-a-big-deal.html?pagewanted=all&_r=2&
Вкратце: Гугл проанализировал десятки тысяч собеседований и их связь с последующей полезностью нанятых сотрудников, и не обнаружил таковой практически вовсе. Зато стало ясно, что обычные методики собеседований ничего не стоят. В частности, головоломки типа «а мы хотим посмотреть, как он мыслит в нестандартной ситуации и под давлением», бесполезны абсолютно и в основном нужны для повышения ч.с.в. интервьюера. Также абсолютно бесполезно смотреть на оценки в дипломе, поэтому Гугл больше ими не интересуется.
А что работает? Вроде бы немного работают вопросы типа «расскажите о сложной ситуации в своей работе, и как вы из нее выбрались», да и то не факт.
В общем, даже Гугл не знает, как проводить собеседования, чего же вы хотите от несчастных гуманитариев из HR, которые верят в сказки, рассказанные им на трехдневных тренингах, и от таких же несчастных тимлидов, которые не знают что спросить, и спрашивают, что вспомнят из статей о Гугле и Эппле? :)
www.nytimes.com/2013/06/20/business/in-head-hunting-big-data-may-not-be-such-a-big-deal.html?pagewanted=all&_r=2&
Вкратце: Гугл проанализировал десятки тысяч собеседований и их связь с последующей полезностью нанятых сотрудников, и не обнаружил таковой практически вовсе. Зато стало ясно, что обычные методики собеседований ничего не стоят. В частности, головоломки типа «а мы хотим посмотреть, как он мыслит в нестандартной ситуации и под давлением», бесполезны абсолютно и в основном нужны для повышения ч.с.в. интервьюера. Также абсолютно бесполезно смотреть на оценки в дипломе, поэтому Гугл больше ими не интересуется.
А что работает? Вроде бы немного работают вопросы типа «расскажите о сложной ситуации в своей работе, и как вы из нее выбрались», да и то не факт.
В общем, даже Гугл не знает, как проводить собеседования, чего же вы хотите от несчастных гуманитариев из HR, которые верят в сказки, рассказанные им на трехдневных тренингах, и от таких же несчастных тимлидов, которые не знают что спросить, и спрашивают, что вспомнят из статей о Гугле и Эппле? :)
вот пара цитат:
«we found that brainteasers are a complete waste of time. How many golf balls can you fit into an airplane? How many gas stations in Manhattan? A complete waste of time. They don’t predict anything. They serve primarily to make the interviewer feel smart. Instead, what works well are structured behavioral interviews, where you have a consistent rubric for how you assess people, rather than having each interviewer just make stuff up.»
«Years ago, we did a study to determine whether anyone at Google is particularly good at hiring. We looked at tens of thousands of interviews, and everyone who had done the interviews and what they scored the candidate, and how that person ultimately performed in their job. We found zero relationship. It’s a complete random mess, except for one guy who was highly predictive because he only interviewed people for a very specialized area, where he happened to be the world’s leading expert.»
«we found that brainteasers are a complete waste of time. How many golf balls can you fit into an airplane? How many gas stations in Manhattan? A complete waste of time. They don’t predict anything. They serve primarily to make the interviewer feel smart. Instead, what works well are structured behavioral interviews, where you have a consistent rubric for how you assess people, rather than having each interviewer just make stuff up.»
«Years ago, we did a study to determine whether anyone at Google is particularly good at hiring. We looked at tens of thousands of interviews, and everyone who had done the interviews and what they scored the candidate, and how that person ultimately performed in their job. We found zero relationship. It’s a complete random mess, except for one guy who was highly predictive because he only interviewed people for a very specialized area, where he happened to be the world’s leading expert.»
Некоторые вопросы задаются не с целью решить «достаточно умный или недостаточно», а с целью понять, как этого человека потом правильно «готовить» и справимся ли мы с этой готовкой.
Грубый пример: Загадки не решает, но код нормально пишет. Гм… Может быть у нас есть достаточно задач без загадок?
Мне вообще кажется, что при минимальном фильтре бездельников и неадекватов, «полезность в перспективе» гораздо больше зависит от того, как человека готовят, чем от начальных умений этого человека.
Грубый пример: Загадки не решает, но код нормально пишет. Гм… Может быть у нас есть достаточно задач без загадок?
Мне вообще кажется, что при минимальном фильтре бездельников и неадекватов, «полезность в перспективе» гораздо больше зависит от того, как человека готовят, чем от начальных умений этого человека.
В одной любопытной книге рассказывают про похожее исследование в армии США.
Результаты те же: за исключением совсем специальных навыков, единственное с чем коррелирует успех человека на службе — это IQ. С другими тестами он связан ровно настолько, насколько эти тесты связаны с IQ.
Результаты те же: за исключением совсем специальных навыков, единственное с чем коррелирует успех человека на службе — это IQ. С другими тестами он связан ровно настолько, насколько эти тесты связаны с IQ.
Вопрос про Pi = 3 на самом деле крутой! Мне бы понравился :) Правда он хоть что-то показывает только если не «подвешивает» человека полностью. А ещё может показать что-то, что не ожидает собеседующий. Но если собеседующие с этим готовы мириться, то вполне хороший вопрос! :)
Вот в вашем случае вы показали кругозор и начитанность. И это дало собеседующему какую-то информацию. Дало информацию, значит вопрос был полезен. Все, больше тут обсуждать нечего.
А тот факт, что человек что-то написал про не очень удачное собеседование у себя в fb, вероятно означает, что собеседует он мало, неопытный и мало реальных чудиков повидал. Зачем его бедненького, маленького, неопытного сразу на хабре мочить? :)
Вот в вашем случае вы показали кругозор и начитанность. И это дало собеседующему какую-то информацию. Дало информацию, значит вопрос был полезен. Все, больше тут обсуждать нечего.
А тот факт, что человек что-то написал про не очень удачное собеседование у себя в fb, вероятно означает, что собеседует он мало, неопытный и мало реальных чудиков повидал. Зачем его бедненького, маленького, неопытного сразу на хабре мочить? :)
Собеседование проводили идиоты, да. Так бывает, переживать не надо, так как даже если бы вы его прошли — вам потом с ними работать. А зачем?
Вопрос про pi = 3 некорректен. Пи — это не физическая константа, а математическая, и мир, в котором pi = 3 не возможен в принципе, в отличие от мира с другой скоростью света или гравитационной постоянной.
Почему не возможен в принципе?
Докажите, что невозможно существование пространства, в котором отношение длины окружности (в терминах того пр-ва) к диаметру было бы равным 3, а не 3.14159...?
Для меня это не совсем очевидно.
Докажите, что невозможно существование пространства, в котором отношение длины окружности (в терминах того пр-ва) к диаметру было бы равным 3, а не 3.14159...?
Для меня это не совсем очевидно.
Пи — это не свойство простраства. Это константа, которая одновременно обладает многими свойствами. Вот к примеру, рассмотрим решение дифференциального уравнения x'' = -x. Как видно, никаких пространств в этом уравнении не фигурирует, однако период любого решения этого уравнения будет равен 2*pi. Тот факт, что пи — это отношение длины окружности к диаметру на евклидовой плоскости равно пи — лишь одно из свойств данной константы.
Как это не фигурирует никакого пространства? Производная считается через предел, предел это понятие топологическое.
Тут, конечно, можно сказать, что это уравнение в кольце с дифференциальным оператором, но в таком случае я не стал бы что-то утвеждать про «любое решение».
Тут, конечно, можно сказать, что это уравнение в кольце с дифференциальным оператором, но в таком случае я не стал бы что-то утвеждать про «любое решение».
Это уравнение на функциях вещественной переменной.
Рассмотрим произвольное арифметическое свойство пи. Ну например, 1 + 1/2^2 + 1/3^2 +… = pi^2/6. Как вы тут можете изменить пространство, чтобы пи стало равно 3?
Рассмотрим произвольное арифметическое свойство пи. Ну например, 1 + 1/2^2 + 1/3^2 +… = pi^2/6. Как вы тут можете изменить пространство, чтобы пи стало равно 3?
Мне не очевидно, почему в какой-нибудь изощренной метрике этот ряд не может сойтись к 3/2.
Довольно очевидно: потому что никакой метрики здесь нет.
Это же вещественные числа. На них есть естественная норма. Более того, метрика здесь вообще не причём. Тот факт что этот ряд сходится к pi^2/6 формулируется в терминах целочисленной арифметики, без всяких метрик. В частности, можно доказать, что сколько бы первых его членов вы не взяли, их сумма будет меньше чем 1.8.
Сумма ряда это предел частичных сумм, как же тут без метрики (или хотя бы топологии или чего-нибудь такого)?
И вообще, слева стоит предел последовательности рациональных чисел. Он не рационален. А уж где мы его возьмём, в вещественных числах или в p-адических — отдельный вопрос.
> их сумма будет меньше чем 1.8.
Вот это к тому, что «естественная норма» согласована со структурой упорядоченного поля, но никак не про «формулируется в терминах целочисленной арифметики».
И вообще, слева стоит предел последовательности рациональных чисел. Он не рационален. А уж где мы его возьмём, в вещественных числах или в p-адических — отдельный вопрос.
> их сумма будет меньше чем 1.8.
Вот это к тому, что «естественная норма» согласована со структурой упорядоченного поля, но никак не про «формулируется в терминах целочисленной арифметики».
Нет, я конечно понимаю, что можно назвать стулья столами, а жигулёвское пиво односолодовым виски. И тогда у нас будут и свиньи летать и число пи будет равно трём.
Только это будет уже не число пи в традиционном понимании.
Только это будет уже не число пи в традиционном понимании.
Это вопрос к тому, почему традиционное понимание именно таковое. Ворос сути, природы наблюдаемого мира.
Есть, к примеру, такое свойство пи, как трансцендентность. Это значит, его нельзя выразить конечной арифметической формулой. А бесконечные прогрессии уже имеют заложенные в их способе определния явные и неявные отношения, то есть — метрику.
Есть, к примеру, такое свойство пи, как трансцендентность. Это значит, его нельзя выразить конечной арифметической формулой. А бесконечные прогрессии уже имеют заложенные в их способе определния явные и неявные отношения, то есть — метрику.
В соседнем комментарии я уже написал, что для того, чтобы прийти к понятию пи никакого наблюдаемого мира не нужно.
И трансцендентность — это не про представимость арифметической формулой. Это тот факт, что число не является корнем полинома с целыми коэффициентами, что неэквивалентно тому, что вы сказали.
И трансцендентность — это не про представимость арифметической формулой. Это тот факт, что число не является корнем полинома с целыми коэффициентами, что неэквивалентно тому, что вы сказали.
Так я ж не спорю! Я просто говорю, что все эти «арифметические свойства» не являются реально арифметическими, потому что сильно используют свойства поля вещественных чисел.
Это как с запретом на использование косинуса в посте: даже если вы его явно не пишете, он всё равно там. Можно его глубже запрятать, но избавиться от него не удастся.
Это как с запретом на использование косинуса в посте: даже если вы его явно не пишете, он всё равно там. Можно его глубже запрятать, но избавиться от него не удастся.
Вещественные числа можно определить на основе натуральных. И потом, я тут приводил примеры, что это равенство выливается во вполне определённые целочисленные неравенства. Можно вообще вещественные числа не упоминать.
Вы, возможно, удивитесь (хотя как выпускник кафедры алгебры не должны), но p-адические числа с тем же успехом вводятся на основе натуральных, надо только пополнение брать по другому нормированию.
Я, видимо, что-то упустил, но я никак не вижу, как избавиться от использования вещественных чисел в определении вещественного числа (которое ни в какие меньшие разумные структуры не попадает).
Я, видимо, что-то упустил, но я никак не вижу, как избавиться от использования вещественных чисел в определении вещественного числа (которое ни в какие меньшие разумные структуры не попадает).
Вещественное число определяется исключительно на основе порядка, определённого на рациональных числах, согласованного с операциями умножения и сложения: вещественным числом x называется любое подмножество множества рациональных чисел Q (отличное от пустого множества и самого Q), которое вместе с каждым своим элементом a содержит все числа, большие его. Числа, задаваемые множествами {x: x>q} и {x: x>=q}, где q — рациональное число, считаются эквивалентными. Они задают вещественное число, которое считается равным числу q.
Пока никаких метрики и топологии не потребовалось. Возможно, они пригодятся дальше, при доказательстве корректности и определении арифметических операций.
Пока никаких метрики и топологии не потребовалось. Возможно, они пригодятся дальше, при доказательстве корректности и определении арифметических операций.
Вы по существу записали то же самое другми словами. Между стандартной метрикой на Q и стандартным порядком там же нет никакой разницы.
Я понимаю, что вы с Олегом мне пытаетесь сообщить, что вещественные числа выделяются среди других пополнений поля рациональных. Я же говорю про то, что когда вы берете предел последовательности (сумма ряда, ага), то надо всегда помнить, в какой топологии этот предел берется.
Как я уже говорил выше: «даже если вы его явно не пишете, он всё равно там». Хотя кажется, что в этой формуле кроме Pi есть только арифметические операции и целые числа, это не так — там есть многоточие, в котором спрятана вся топологическая часть.
Я понимаю, что вы с Олегом мне пытаетесь сообщить, что вещественные числа выделяются среди других пополнений поля рациональных. Я же говорю про то, что когда вы берете предел последовательности (сумма ряда, ага), то надо всегда помнить, в какой топологии этот предел берется.
Как я уже говорил выше: «даже если вы его явно не пишете, он всё равно там». Хотя кажется, что в этой формуле кроме Pi есть только арифметические операции и целые числа, это не так — там есть многоточие, в котором спрятана вся топологическая часть.
Порядок, конечно определяет какую-нибудь интервальную топологию, но пока необходимости в ней нет. Вы можете взять её хоть дискретной — конструкция останется той же самой. Где спрятан предел в определении числа как монотонного подмножества рациональных чисел? Да, после того, как мы введём топологию эпсилон-окрестностей, мы докажем, что наше вещественное число — это нижняя грань некоторого подмножества образов рациональных чисел в нашем построенном множестве R. Но до того мы этого сказать не сможем (нижняя грань где? Вещественных чисел ещё нет, мы их только определяем), да и не захотим, пока в конструкции это не нужно.
Я правильно понимаю, что ваш вопрос таков: если у нас есть только натуральные числа, и мы не знаем никакой геометрии, почему нам придёт в голову пополнить рациональные числа именно до вещественных, а не до p-адических?
Ответ: потому, что вещественные числа тупо полезнее, даже в той же теории чисел или комбинаторике. Ну вот чему, к примеру равна вероятность, что в случайной перестановке из n элементов есть элемент, оставшийся на своём месте? Она равна примерно 1/e. Я может быть чего-то не догоняю, но я не уверен, что тот же факт можно вывести с помощью p-адических чисел.
Ответ: потому, что вещественные числа тупо полезнее, даже в той же теории чисел или комбинаторике. Ну вот чему, к примеру равна вероятность, что в случайной перестановке из n элементов есть элемент, оставшийся на своём месте? Она равна примерно 1/e. Я может быть чего-то не догоняю, но я не уверен, что тот же факт можно вывести с помощью p-адических чисел.
а что такое целочисленная арифметика?
Например, арифметика Пеано.
Сумма первых 7-и членов этого ряда уже больше 3/2.
Забавно, почему Вы назвали арифметическое свойство предела бесконечной последовательности арифметическим свойством числа пи :)
Вопрос то куда проще. Вот, Вы измеряете доступными способами число пи, и обнаруживаете его равным трем. Каким Вы видите мир? Возможен ли такой мир без разрушения топологии?
Вы же вместо решния задачи ограничиваете свою возможность ее решить, вводя дополнительные ограничния, ри которых задача решния не имеет.
А весь вопрос заключен в способности наблюдателя производить измерения и определения понятия круга для произвольной топологии.
Вопрос то куда проще. Вот, Вы измеряете доступными способами число пи, и обнаруживаете его равным трем. Каким Вы видите мир? Возможен ли такой мир без разрушения топологии?
Вы же вместо решния задачи ограничиваете свою возможность ее решить, вводя дополнительные ограничния, ри которых задача решния не имеет.
А весь вопрос заключен в способности наблюдателя производить измерения и определения понятия круга для произвольной топологии.
Давайте поговорим о том, что такое число пи. Вот предположим, мы с вами — программы в памяти компьютера и никакого пространства у нас вообще нет. Ни двумерного, ни трёхмерного — никакого. Есть байтики.
Но мы какие попало программы, мы у умные, и поэтому изобрели математику. Ни о какой геометрии, конечно, речь не идёт, так как у нас нет пространства. Но вот натуральные числа мы придумали. Потом придумали рациональные, чтобы можно было оценивать, к примеру, вероятности. Потом пришли к концепции полноты пространства и определили вещественные числа и придумали анализ.
И тут хлоп, мы внезапно обнаружили, что во многих наших формулах появляется одна и та же константа. Продолжили мы экспоненту на комплексные числа — а у неё период 2*X*i оказался. Или посчитали сумму приведённого выше ряда, она оказалась равна X^2/6. Ну и так далее. Во многих-многих формулах вылезает одна и та же константа. Ну и решили её назвать pi. Вот и сказочке конец.
А то что вы спрашиваете — это не про значение пи, а про то, что мы померили длину какой-то окружности, и она оказалась в 3 раза больше её диаметра. Ну что поделаешь, кривое пространство, с кем не бывает. Только pi-то тут причём?
Но мы какие попало программы, мы у умные, и поэтому изобрели математику. Ни о какой геометрии, конечно, речь не идёт, так как у нас нет пространства. Но вот натуральные числа мы придумали. Потом придумали рациональные, чтобы можно было оценивать, к примеру, вероятности. Потом пришли к концепции полноты пространства и определили вещественные числа и придумали анализ.
И тут хлоп, мы внезапно обнаружили, что во многих наших формулах появляется одна и та же константа. Продолжили мы экспоненту на комплексные числа — а у неё период 2*X*i оказался. Или посчитали сумму приведённого выше ряда, она оказалась равна X^2/6. Ну и так далее. Во многих-многих формулах вылезает одна и та же константа. Ну и решили её назвать pi. Вот и сказочке конец.
А то что вы спрашиваете — это не про значение пи, а про то, что мы померили длину какой-то окружности, и она оказалась в 3 раза больше её диаметра. Ну что поделаешь, кривое пространство, с кем не бывает. Только pi-то тут причём?
Вы попали в старую ловушку формальной логики. Во-первых, Вы не проверили, появится ли у Вас пи, или нет, до тех пор, пока Вы не свяжете топологически два пространства чисел. Пока Вы находитесь в операциях над числами расширяющими поля, у Вас не появится тригонометрия. Пока Вы не введете ортогональность, у Вас не будет периодичности, а поле комплексных чисел не приведет Вас к тригонометрии, Вы не сможете ее определить.
Пока у Вас нет связанного пространства, у Вас нет топологии и нет никаких особых чисел. Все особые числа определены операционно. И одномерные преобразования сами по себе никогда не дают дополнительной метрики. Она не нужна.
Пока у Вас нет связанного пространства, у Вас нет топологии и нет никаких особых чисел. Все особые числа определены операционно. И одномерные преобразования сами по себе никогда не дают дополнительной метрики. Она не нужна.
Какие пространства чисел? И причём тут пи? И где я упоминал тригонометрию?
То то и оно, что Вы ее не упомянули. Значит не понимаете, как двумерность определяет пи, но никакие операции без двумерности числа пи не дадут никогда.
Можете проверить Вашу модель с программами в памяти. Приведите логическую последовательность, которая выявляет в свойствах чисел и операций над ними число пи и Вы увидите, что это свойства ортогональной связи (или какой-то другой) чисел, помимо определенных над полем операций.
Как только дойдете до функций, задумайтесь хорошенько, чем они отличаются от операций.
Можете проверить Вашу модель с программами в памяти. Приведите логическую последовательность, которая выявляет в свойствах чисел и операций над ними число пи и Вы увидите, что это свойства ортогональной связи (или какой-то другой) чисел, помимо определенных над полем операций.
Как только дойдете до функций, задумайтесь хорошенько, чем они отличаются от операций.
Мне кажется, вы троллите. Что такое «ортогональная связь чисел»? Я в посте выше написал последовательность выведения числа пи без геометрии. Если нужно, могу подробнее, я в ней все шаги хорошо понимаю.
Да, мне интересно увидеть введение числа пи в рамках теории множеств или полей чисел.
А что такого? Натуральные числа в теории множеств вводятся. Рациональные получаются автоматом. Вещественные — как сечения рациональных. Функции в теории множеств сразу есть. Непрерывность и прочий анализ выводятся с эпсилонами по Коши. Дальше естественным образом появлется экспонента и тригонометрические функции как решения дифференциальных уравнений.
Не так уж и автоматом (выше упоминали про p-адические числа). Но если мы догадаемся использовать архимедову метрику и будем поддерживать линейный порядок, то вещественных чисел, в самом деле, не избежать. При условии, что в нашем мире вообще есть конечные множества (и, как следствие, натуральные числа). У нас они возникли, потому что мы видим мир в виде множества изолированных объектов. А если бы математику решили начать сразу с каких-нибудь волновых функций, то до понятия числа могли бы не дойти вообще. Но я не очень пытался такое представить.
Ортогональная связь это, к примеру, комплексные числа. Где возникает, по сути, вектор. Это и есть топология. Я бы хотел увидеть введение комплексной плоскости вне определения топологии и топологических свойств
Комплексные числа появляются не как векторы, а чисто алгебраически, как алгебраическое замыкание вещественных. Появились они из несколких разных задач никак не связанных с геометрией.
Только без введения геометрии возникает вопрос полноты этих чудесных чисел
Одно дело, корни уравнений с вещественными числсми, совсем другое, понимание ортогональности действительной и мнимой части и введение плоскости комплексных чисел и применение к ней геометрии, которая была взята из реального мира.
Попробуйте остаться в рамках одномерного мира для выведения пи. И вот уже в таком мире комплексные числа будут не получившей развития причудой. Найдите негеометрический способ возведения в комплексную степень. И помните, у вас нет углов, синусов, векторов. Ваш мир однообразен, он не может обнаружить периодичность через геометрию. Все числа изначально последовательны, где это Вы встречали периодичность?
Одно дело, корни уравнений с вещественными числсми, совсем другое, понимание ортогональности действительной и мнимой части и введение плоскости комплексных чисел и применение к ней геометрии, которая была взята из реального мира.
Попробуйте остаться в рамках одномерного мира для выведения пи. И вот уже в таком мире комплексные числа будут не получившей развития причудой. Найдите негеометрический способ возведения в комплексную степень. И помните, у вас нет углов, синусов, векторов. Ваш мир однообразен, он не может обнаружить периодичность через геометрию. Все числа изначально последовательны, где это Вы встречали периодичность?
Легко.
Комплексные числа появились когда придумали формулы для корней кубического уравнения. С ними была следующая проблема: в формуле для абсолютно законных вещественных корней появлялись квадратные корни из отрицательных чисел. Ладно бы уравнение изначально не имело вещественных корней, тогда это никого бы не смутило, но тут-то корень был и его в каком-то смыле можно было вычислить… Собственно, для этого и пришлось придумывать комплексные числа как костыли для проведения этих вычислений.
Как видите, никакой ортогональности и геометрии.
Комплексные числа появились когда придумали формулы для корней кубического уравнения. С ними была следующая проблема: в формуле для абсолютно законных вещественных корней появлялись квадратные корни из отрицательных чисел. Ладно бы уравнение изначально не имело вещественных корней, тогда это никого бы не смутило, но тут-то корень был и его в каком-то смыле можно было вычислить… Собственно, для этого и пришлось придумывать комплексные числа как костыли для проведения этих вычислений.
Как видите, никакой ортогональности и геометрии.
Нет, Вы все еще не видите. Сделайте формализацию комплексных чисел без геометрии. Далеко Вы уйдете? Пока не была введена комплексная плоскость и геометрические преобразования не были применены, это был просто способ показать на неполноту поля вещественных чисел.
Как Вы будете исследовать без представлений о геометрии? Предложите идею.
Как Вы будете исследовать без представлений о геометрии? Предложите идею.
Я что-то не понял. Вводим i, и дальше естественным образом продолжаем все операции. Вполне можно обойтись без геометрического представления.
Обойдитесь. Ввели i. Следующий шаг — какой?
Если честно, я уже начал утомляться пересказывать всю математику.
Но ладно. Итак, мы хотим, чтобы на корни из отрицательных чисел распространились арифметические действия, и эти действия сохранили все свои свойства.
sqrt(-a) = sqrt(-1 * a) = sqrt(-1) * sqrt(a) = i * sqrt(a)
a * i + b * i = (a + b) * i
i * i = sqrt(-1) * sqrt(-1) = -1
(a + b*i) * (c + d*i) = a*c + a*(d*i) + (b*i)*c + (b*i)*(d*i) = a*c + (a*d)*i + (b*c)*i + (b*d) * (i*i) = (a*c — b*d) + (a*d + b*c) * i
Ну и так далее.
Но ладно. Итак, мы хотим, чтобы на корни из отрицательных чисел распространились арифметические действия, и эти действия сохранили все свои свойства.
sqrt(-a) = sqrt(-1 * a) = sqrt(-1) * sqrt(a) = i * sqrt(a)
a * i + b * i = (a + b) * i
i * i = sqrt(-1) * sqrt(-1) = -1
(a + b*i) * (c + d*i) = a*c + a*(d*i) + (b*i)*c + (b*i)*(d*i) = a*c + (a*d)*i + (b*c)*i + (b*d) * (i*i) = (a*c — b*d) + (a*d + b*c) * i
Ну и так далее.
И при чем здесь пи? Вы суть дискуссии помните?
Ох. Ладно. Следующие два шага:
a^2 + b^2 = |(a + b*i) * (a — b*i)| = |a + b*i| * |a — b*i|
Определили модуль как sqrt(a^2 + b^2). Раз есть модуль, есть сходимость.
Определяем exp(z) = 1 + z/1! + z^2/2! + z^3/3! +…
Замечаем что существует такое Z отличное от 0, что exp(Z) = 1. Определяем pi = Z / (2*i).
a^2 + b^2 = |(a + b*i) * (a — b*i)| = |a + b*i| * |a — b*i|
Определили модуль как sqrt(a^2 + b^2). Раз есть модуль, есть сходимость.
Определяем exp(z) = 1 + z/1! + z^2/2! + z^3/3! +…
Замечаем что существует такое Z отличное от 0, что exp(Z) = 1. Определяем pi = Z / (2*i).
Не пойдет. Как Вы определили модуль? Это геометрическая связь а и б. Введенная метрика, имеющая смысл как рассояние в пространстве.
Далее еще хуже. Зачем Вы определили пи? Чем оно Вашем случае особенное? Так можно определить любое число.
Более того, Вы просто развернулиисторический процесс.
Приведите вывод экспоненты как степенного ряда. Зачем она могла понадобиться, в решении каких задач?
Далее еще хуже. Зачем Вы определили пи? Чем оно Вашем случае особенное? Так можно определить любое число.
Более того, Вы просто развернулиисторический процесс.
Приведите вывод экспоненты как степенного ряда. Зачем она могла понадобиться, в решении каких задач?
Модуль я определил пользуясь исключительно свойством |a| * |b| = |a * b|. Я определил модуль чтобы определить сходимость ряда.
Экспонента была придумана для того, чтобы облегчить умножение. Переводили числа в их экспоненты по таблице, складывали и переводили обратно. Использовалась именно экспонента, а не любая друга степенная функция, поскольку exp(x) при малых x очень близко к 1 + x, что сильно облегчает вычисления.
Вывод степенного ряда для экспоненты посмотрите в учебнике. Использовать его для того, чтобы продолжить экспоненту на комплексные числа — естественное решение.
Наконец, почему я определил пи — а) потому что вы просили определить его без геометрии, б) потому что точно та же констата вылезает при решении многих других задач, включая решение приведённого мной дифура и сумму ряда с обратными квадратами.
Увы, это будет мой последний вам ответ. Право слово, я готов найти своему времени лучшее применение, чем пересказ учебников.
Экспонента была придумана для того, чтобы облегчить умножение. Переводили числа в их экспоненты по таблице, складывали и переводили обратно. Использовалась именно экспонента, а не любая друга степенная функция, поскольку exp(x) при малых x очень близко к 1 + x, что сильно облегчает вычисления.
Вывод степенного ряда для экспоненты посмотрите в учебнике. Использовать его для того, чтобы продолжить экспоненту на комплексные числа — естественное решение.
Наконец, почему я определил пи — а) потому что вы просили определить его без геометрии, б) потому что точно та же констата вылезает при решении многих других задач, включая решение приведённого мной дифура и сумму ряда с обратными квадратами.
Увы, это будет мой последний вам ответ. Право слово, я готов найти своему времени лучшее применение, чем пересказ учебников.
Мне Ваши ответы и не нужны. Оказалось все очень просто, Вы не понимаете, как и откуда появляются все эти пи. Для Вас это просто странная константа которая отовсюду лезет сама собой.
Однако соглашаться с Вами в этом резона нет. Вы прагматик, пользуетесь математикой утилитарно и не любите ее исследовать.
Студентам все подают на блюдечке, чего еще ожидать-то. Применять научились и то — отлично.
Вот только зачем Вы тут трудились — непонятно, Вы так и не поняли своей ошибки. Зато уверены, что сделали свое дело хорошо.
И вот это очень плохо.
Однако соглашаться с Вами в этом резона нет. Вы прагматик, пользуетесь математикой утилитарно и не любите ее исследовать.
Студентам все подают на блюдечке, чего еще ожидать-то. Применять научились и то — отлично.
Вот только зачем Вы тут трудились — непонятно, Вы так и не поняли своей ошибки. Зато уверены, что сделали свое дело хорошо.
И вот это очень плохо.
Вы случайно не имеете в виду теорию, по которой «pi» возникает как проявление инвариантности пространства при поворотах, а «e» — как проявление существования преобразований подобия? Где-то я такое видел. Наверное, можно попытаться принять её за основу. Но почему это лучше, чем идти через теорию множеств, архимедову метрику и матанализ, не знаю. Можно придумать много наборов аксиом, все они дадут одну математику (в её современном понимании, где есть такие понятия, как «аксиома», «теорема», «доказательство» и «закон исключенного третьего»).
Одна система аксиом лучше другой, если она состоит из меньшего количества эмпирических утверждений и даёт сравнимое пространство следствий… Иначе говоря, вариант, когда Пи лезет само по себе из разных аксиом хуже варианта, когда аксиома про Пи одна, а всё остальное, что Пи упоминает, из неё так или иначе следует.
Этого свойства не достаточно для однозначного определения модуля. f(x)=1 обладает ровно таким же свойством.
Само собой, модуль на комплексных числах должен быть продолжением вещественного.
И ещё должно выполняться неравенство треугольника. На всякий случай.
Как только Вы этот модуль используете как меру расстояния между числами при определении предела — в этот момент Вы превращаете поле действительных чисел в метрическое пространство, о чем Вам тут уже давно намекают.
Но число pi от этого не становится более геометрическим. Хотя, конечно, оно является следствием использования архимедовой метрики.
Как бы сказать. Конечно, по-идее оно будет метрическим. Но для того, чтобы говорить о пределах и т.п., знать об этом вовсе не нужно. Более того, вещественный анализ был придуман задолго до понятия метрического пространства.
Когда придумывали анализ, пространство тоже было только евклидовым и мера казалась естественной и единственной. С тех пор математика на месте не стояла. Посмотрите уже на определение предела последовательности. Там обязательно или используется или мера или топологические св-ва пространства.
Вероятно, вы имели в виду не меру, а метрику, но не суть.
Вы возможно удивитесь, но я готов дать определение предела последовательности вещественных чисел, не употребляя слов «метрика» и «топология».
Вы возможно удивитесь, но я готов дать определение предела последовательности вещественных чисел, не употребляя слов «метрика» и «топология».
Ну, модуль и расстояние сами по себе — это одномерные понятия, и Пи тут ещё нету.
Я прекрасно знаю всю эту математику, не надо ее пересказывать. Просто доведите рассуждения до конца, там где у Вас хоп и получается пи без геометрии.
Вы сами себя утомляете, не вздумайте на меня обижаться.
Вы сами себя утомляете, не вздумайте на меня обижаться.
Ну, раз вы такой умный, расскажите нам, неучам, пожалуйста, в чем соль. Я без троллинга и без наезда, я абсолютно серьезно.
Соль увы, не излагается в нескольких абзацах. Просто нужно знать, что мат. анализ, который излагается на первых курсах вузов — это частный случай, однако имеющий широчайшее применение в нашем почти евклидовом приземном пространстве. Понятие метрики (или сразу нормы) применяется уже при определении предела и дальше, таким образом, присутствует в большинстве результатов. Однако даже в нерелятивистской физике иногда нужны другие определения пространства аргумента функции.
Здесь вообще можно вспомнить и о матричном представлении комплексных чисел, чтобы все операции распространить?
Двумерность, и все её геометрические следствия, в том числе и Пи, возникают при введении операций произведения и обратной ей операции извлечения корня.
Первый раз — чуть раньше появились. «В рамках формального решения задачи по вычислению двух чисел, которые в сумме дают 10, а при перемножении дают 40». При этом получилось квадратное уравнение и комплексные корни.
А где перемножение — там уже двумерность, при представлении перемножаемого в виде прямоугольника на числовой плоскости. С её метрикой.
А где перемножение — там уже двумерность, при представлении перемножаемого в виде прямоугольника на числовой плоскости. С её метрикой.
Чтобы понять, что пространство рациональных чисел не полно вам не нужна метрика — дело в том, что если вы возьмете наиболее естественную для Q топологию (с базой открытых отрезков (x1, 2)), то вы не найдете никакой метрики, которая бы индуцировала такую топологию и, при этом, была бы полна.
После того, как это становится понятным, следующим шагом является ввод какой-нибудь удобной метрики (например, наиболее простой — задаваемой модулем разности) и пополнение пространства пределами.
Кстати, R не единственное такое расширение Q. Вы можете, например, определить такие объекты, как ультрафильры и построить с помощью них другие интересные пространства — например, пространство гиперреальных чисел, в котором будут существовать объективные бесконечно малые и бесконечно большие. Однако, все эти конструкции значительно менее тривиальны, чем евклидова метрика.
Исходя из вышесказанного я бы все-таки сделал вывод, что пи можно сконструировать без какой-либо геометрии.
После того, как это становится понятным, следующим шагом является ввод какой-нибудь удобной метрики (например, наиболее простой — задаваемой модулем разности) и пополнение пространства пределами.
Кстати, R не единственное такое расширение Q. Вы можете, например, определить такие объекты, как ультрафильры и построить с помощью них другие интересные пространства — например, пространство гиперреальных чисел, в котором будут существовать объективные бесконечно малые и бесконечно большие. Однако, все эти конструкции значительно менее тривиальны, чем евклидова метрика.
Исходя из вышесказанного я бы все-таки сделал вывод, что пи можно сконструировать без какой-либо геометрии.
Устроит один конкретный пример вывода числа пи без геометрии
В дополнение к тому, что я писал выше: если у нас есть только вещественные числа (и никакой геометрии), и мы решим на них дифференциальное уравнение y'' = -y, мы получим синус. Чем не вывод пи без геометрии?
Нельзя. Связь времени и пространства это уже топологияи именно в ней содержится это самое пи.
Откуда Вы возьмете эту связь, если у Вас нет пространства, а значит нет времени и нет движения?
Ортогональность измерний пространстваи времен задает геометрю пространства и порождает пи как один из параметров связи.
Ие ещекозыри в рукаве?
Откуда Вы возьмете эту связь, если у Вас нет пространства, а значит нет времени и нет движения?
Ортогональность измерний пространстваи времен задает геометрю пространства и порождает пи как один из параметров связи.
Ие ещекозыри в рукаве?
Да, планшет пока не средство для работы. Так, котят полайкать. Никак не найду достойную клавиатуру. Стандартная от самсунга — тупая. Умная — не отрабатывет все нажатия и ридумывает страшные замены… в результате отправляю текст шизодного маньяка
Нет никакого времени и пространства.
Есть функции вещественной переменной. Мы задаёмся вопросом, какая функция отвечает функциональному соотношению y''(x) = -y(x).
Есть функции вещественной переменной. Мы задаёмся вопросом, какая функция отвечает функциональному соотношению y''(x) = -y(x).
В каком базисе? Если Вы не вводите базис, у Вас нет и поисков функций.
Вы говорите о соотношении, подумайте, пи относится к свойствам этого соотношения или нет?
Базис это геометрия.
Вы говорите о соотношении, подумайте, пи относится к свойствам этого соотношения или нет?
Базис это геометрия.
Какой базис?! Это функция действительной переменной. Одномерная.
Дифференцируем по ней же? Посмотрите у это одна переменная. Х другая.
y — это не переменная. Это функция. Для определения производной y(x) по x не нужны никакие базисы.
Жесть. Вы утверждаете, что между х и у не вводится связь?
Вы утверждаете, что у семейства функций нет единого базиса?
Декарт не нужен. Я умываю руки, можете минусовать сколько влезет.
Вы утверждаете, что у семейства функций нет единого базиса?
Декарт не нужен. Я умываю руки, можете минусовать сколько влезет.
Для определения производной нужно вводить понятие предела, а для него обязательно разбираться со свойствами пространства аргумента и того утверждения, что это действительные числа не достаточно. Обязательно потребуется или введение метрики или какое-либо описание топологических свойств. В том определении, которое Вы почему-то считаете единственно возможным, пространство аргумента — это множество действительных числ (непрерывное упорядоченное поле) с метрикой m(a,b) = {b-a при b >= a и a-b в остальных случаях}. Однако даже на том же поле действительных чисел можно ввести другие, например, метрики и получить совсем другие производные.
Однако даже на том же поле действительных чисел можно ввести другие, например, метрики и получить совсем другие производные.
Хм. Когда мы вводим метрику на поле, мы хотим, чтобы сложение и умножение оставались в этой новой метрике непрерывными. А ещё было бы неплохо, чтобы dist(a+c,b+c)=dist(a,b) и dist(0,a*b)=dist(0,a)*dist(0,b). Есть ли хоть одна нетрадиционная метрика с этими условиями, не сводящаяся к автоморфизму поля R?
У Вас уже тут x и y, это уже два измерения. Приплыли. Плоскость и её свойства уже все с Вами.
Я вот могу и 5 переменных в одной формуле написать, а в 5-мерном пространстве никогда не жил.
Ну, я в двумерных и одномерных тоже не бывал, но вот свойства их изучать мне это не мешает.
Жить не жил, а работать приходилось...
А в каком месте вы перешли от геометрии к топологии? Топологические пространства можно найти где угодно, и действительно, без них не очень удобно определять полноту, непрерывные функции и т.п. (эпсилон-дельта подход матана это хорошо, но он не более, чем скрытая топология). Но откуда возьмётся геометрия? Да, её построят в качестве математического курьёза (метрическое пространство, элементами которого являются пары действительных чисел; метрика определяет топологию). Так же, как мы строим многомерные пространства, пространства Лобачевского и пространства последовательностей с метрикой L_\infty. Но число pi, которое там будет появляться, мы, скорее всего встретим, как интеграл от sqrt(1-x^2) — объект, давно знакомый нам по работе с числами и функциями (правда, зачем он нам понадобился — сказать трудно. Если мы существа одномерные, то интеграл — путь, пройденный при переменной скорости, а если программы — то очередной математический курьёз?) Но в любом случае, pi приходит не из геометрии, а из матанализа.
Давайте вернемся к полноте целых чисел. Мы же понимаем, что рациональные дроби это не шаг в сторону полноты. Как от целых чисел перейти к вещественным? Здесь топология как обобщение метрики — анахронизм. Нельзя определить обобщение метрики, если у нас нет метрики. Нельзя ввести метрику без пространства. Вводя пространство мы вводим связанность. Связанность имеет скрытые параметры связи, которые мы потом радостно вычислим.
Итак, у нас есть целые числа, что дальше?
Ввели мы умножение, деление, степень, корень, мнимые числа.
Как мы свяжем мнимые числа с действительными? Как поймем неполноту и исследуем дополнение, не введя второго измерения с присущими ему свойствами связи в виде угла вектора?
Итак, у нас есть целые числа, что дальше?
Ввели мы умножение, деление, степень, корень, мнимые числа.
Как мы свяжем мнимые числа с действительными? Как поймем неполноту и исследуем дополнение, не введя второго измерения с присущими ему свойствами связи в виде угла вектора?
Про переход от вещественным к комплексным написал выше.
Про переход от целым к вещественным:
1. От целых к рациональным один шаг.
2. Определяем вещественные числа как сечения рациональных. Сечение — разбиение рациональных на два множества таких что в одном все элементы меньше всех элементов другого.
Про переход от целым к вещественным:
1. От целых к рациональным один шаг.
2. Определяем вещественные числа как сечения рациональных. Сечение — разбиение рациональных на два множества таких что в одном все элементы меньше всех элементов другого.
Уже этот переход под вопросом. Зачем он? Для чего не хватает рациональных дробей? Для иррациональных чисел, возникающих при извлечении корней. Их не представить конечными дробями. Но нет способа получить любые иррациональные числа. И, что у нас с полнотой? Нет ее. И как движущий наш прогресс механизм поисков полноты — сломался.
Для чего вещественные числа? Например для того, чтобы можно было работать с непрерывными функциями, а это очень-очень полезная возможность, даже если вокруг нас нет никакого пространства.
Вот мы и пришли к функциям. Функции это отображения одного пространства в другое. Привет топологии и скрытым параметрам связи.
Функция — это отображение любого множества в любое. Для того, чтобы рассматривать функции, никакая топология не нужна.
А что такое отображение как не определение связи?
Далее происходит обобщение до пространства и введение метрики.
Как только мы это сделаем, мы спрячем пи. Которое потом начнет всплывать.
Если все еще не видите, попробуйте не обобщая отображения до геометрически инвариантной связи (ортогональность, дающая возможность вычислять расстояние) определить число пи хоть в каких-то вычислениях как особое число, связывющее числа внутри поля или множества.
Далее происходит обобщение до пространства и введение метрики.
Как только мы это сделаем, мы спрячем пи. Которое потом начнет всплывать.
Если все еще не видите, попробуйте не обобщая отображения до геометрически инвариантной связи (ортогональность, дающая возможность вычислять расстояние) определить число пи хоть в каких-то вычислениях как особое число, связывющее числа внутри поля или множества.
Наша беседа зашла в тупик.
Я Вам больше скажу. Пи это обобщение поворота отображения одного множества в другое по их функции связи. Чисто геометрический казус. Где бы Вы ни нашли пи, будет и ортогональная связь множеств, с заданной формулой расстояния между парами значений из множеств. Как только уберете метрику, исчезнет и пи.
Если бы вы не использовали некие термины, понятные только вам и не имеющие какого-либо общепринятого значения, на ваши вопросы было бы гораздо проще ответить.
Для начала попробуйте ответить на следующие вопросы:
1. Что такое «скрытые параметры связи»?
2. Что такое «связность» в вашем понимании?
Для начала попробуйте ответить на следующие вопросы:
1. Что такое «скрытые параметры связи»?
2. Что такое «связность» в вашем понимании?
Если бы Вы не утверждали, что число пи особое само по себе, вне геометрии, не пришлось бы забираться в то, где математика исследует сама себя.
Итак, когда мы определяем функцию — это связанность множеств. Надеюсь это понятно.
Когда мы определяем анализ мы определяем базис — метрику связи любых пар в множестве. Например, расстояние. Так мы определяем пространство и его топологию.
Введя эту связь мы определяем явные параметры.
Теперь, анализируя связанные метрикой множества, мы можем обнаруживать некоторые неявные связи, некие константы, инвариантные в этом пространстве.
Это значит, что геометрические параметры никогда не являлись свойствами чисел или несвязанных их множеств, только свойствами введенных связей между множествами
Итак, когда мы определяем функцию — это связанность множеств. Надеюсь это понятно.
Когда мы определяем анализ мы определяем базис — метрику связи любых пар в множестве. Например, расстояние. Так мы определяем пространство и его топологию.
Введя эту связь мы определяем явные параметры.
Теперь, анализируя связанные метрикой множества, мы можем обнаруживать некоторые неявные связи, некие константы, инвариантные в этом пространстве.
Это значит, что геометрические параметры никогда не являлись свойствами чисел или несвязанных их множеств, только свойствами введенных связей между множествами
Все-таки вещь, которую Вы называете базисом, принято называть базой (хотя базис тоже допустим, но так никто не говорит, потому что можно перепутать с базисом векторного пространства). Топологию можно определить и без метрики, просто постулировав. Функцию никто связанностью никогда не называет. Все-таки нужно использовать нормальную терминологию, иначе Вас не будут понимать.
Теперь по сути. Если вы возьмете пространство R', удовлетворяющее следующим аксиомам:
1. R' — поле.
2. R' линейно упорядочено.
3. R' полно по Дедекинду (нет сечений без точных граней одновременно сверху и снизу).
То такое пространство будет обычным R с точностью до гомоморфизма с алгебраической точки зрения.
Теперь мы можем рассмотреть последовательности в этом пространстве, которые определяются функциями f: N->R. Линейной упорядоченности пространства достаточно, чтобы сконструировать на нем фильтры. Категорные пределы по этим фильтрам дадут способ сопоставить каждой последовательности число из R или установить расходимость такой последовательности.
Частичные суммы ряда являются как раз последовательностями. Конструкция предела, описанная выше, позволяет сопоставить ряд элементу R. Таким образом бы можем вычислять различные числа, типа пи, e и т.п.
Если двигаться дальше, то можно рассмотреть функции R->R и синтетически, с помощью того же аппарата определить дифференциальный оператор. Спектром этого оператора будут экспоненты.
Теперь, если мы рассмотрим алгебраическое замыкание этого R, мы получим C. Поскольку у нас есть экспоненты и pi, мы можем вычислить exp(i*pi), чисто алгебраически.
Ну и так далее. Я это все к чему — я не утверждал, что геометрия не нужна, я просто утверждал, что определение pi через окружность в R^2 гораздо естественнее и фундаментальнее, чем определение, которое зависит от кривизны. Конструкция, приведенная выше — просто в доказательство моих слов, о том, что впринципе, для определения этих объектов достаточно только алгебры и базовой теории множеств.
Теперь по сути. Если вы возьмете пространство R', удовлетворяющее следующим аксиомам:
1. R' — поле.
2. R' линейно упорядочено.
3. R' полно по Дедекинду (нет сечений без точных граней одновременно сверху и снизу).
То такое пространство будет обычным R с точностью до гомоморфизма с алгебраической точки зрения.
Теперь мы можем рассмотреть последовательности в этом пространстве, которые определяются функциями f: N->R. Линейной упорядоченности пространства достаточно, чтобы сконструировать на нем фильтры. Категорные пределы по этим фильтрам дадут способ сопоставить каждой последовательности число из R или установить расходимость такой последовательности.
Частичные суммы ряда являются как раз последовательностями. Конструкция предела, описанная выше, позволяет сопоставить ряд элементу R. Таким образом бы можем вычислять различные числа, типа пи, e и т.п.
Если двигаться дальше, то можно рассмотреть функции R->R и синтетически, с помощью того же аппарата определить дифференциальный оператор. Спектром этого оператора будут экспоненты.
Теперь, если мы рассмотрим алгебраическое замыкание этого R, мы получим C. Поскольку у нас есть экспоненты и pi, мы можем вычислить exp(i*pi), чисто алгебраически.
Ну и так далее. Я это все к чему — я не утверждал, что геометрия не нужна, я просто утверждал, что определение pi через окружность в R^2 гораздо естественнее и фундаментальнее, чем определение, которое зависит от кривизны. Конструкция, приведенная выше — просто в доказательство моих слов, о том, что впринципе, для определения этих объектов достаточно только алгебры и базовой теории множеств.
Проблема чисто алгебраического подхода в бесцельности. Нет движущего фактора определять именно эти числа. Ценность этих чисел в удобстве. Вы предложили рассмотреть принцип полноты.
Да, действительно, можно получить больше вещественных чисел с помощью пределов. Доказано ли, что все?
Насчет терминологии у меня есть извинение. Я увлекаюсь обратной стороной математики. Причина проста. Гёдель вполне доказал, что нужно выходить за рамки формальных систем, чтобы их проверить.
Числа это не первое обобщение. Неупорядоченные счетные множества самометричны. Я понимаю, что это еще один термин. Однако, выводя из них дальнейшие обобщения, хорошо видно, где свойства чисел, где свойства операций. Над числами, где свойства метрик.
Топологию можно формально ввести без метрик, да. Но без введения метрик эта топология неаналитична.
Предмет то спора оказался не так уж прост
1. Особые числа это свойство топологии (связанности по семейству метрик) или свойство операций над числами
2. Можно ли ввести функции без определения топологии отображения и разделения множеств на непересекающиеся. Здесь вопрос к базе и к базису. Их следует различать, однако у них одно обобщение.
3. Реальна ли в принципе алгебра без геометрических методов (т.е. без определения геометрических свойствих как расстояние) при введении второго измерения для определения функций как геометрии отображений.
А причина спора проста. Насколько связно математик должен представлять главные обобщения, чтобы ответить на вопрос о наблюдаемом мире при тех или иных вычисленных значениях модели этого мира?
Что если синус окажется больше единицы?
Это ведь вопрос того, что значит синус и что значит единица.
И если обобщения этого порядка по сути заучены, знания невозможно применить к ситуации.
Да, действительно, можно получить больше вещественных чисел с помощью пределов. Доказано ли, что все?
Насчет терминологии у меня есть извинение. Я увлекаюсь обратной стороной математики. Причина проста. Гёдель вполне доказал, что нужно выходить за рамки формальных систем, чтобы их проверить.
Числа это не первое обобщение. Неупорядоченные счетные множества самометричны. Я понимаю, что это еще один термин. Однако, выводя из них дальнейшие обобщения, хорошо видно, где свойства чисел, где свойства операций. Над числами, где свойства метрик.
Топологию можно формально ввести без метрик, да. Но без введения метрик эта топология неаналитична.
Предмет то спора оказался не так уж прост
1. Особые числа это свойство топологии (связанности по семейству метрик) или свойство операций над числами
2. Можно ли ввести функции без определения топологии отображения и разделения множеств на непересекающиеся. Здесь вопрос к базе и к базису. Их следует различать, однако у них одно обобщение.
3. Реальна ли в принципе алгебра без геометрических методов (т.е. без определения геометрических свойствих как расстояние) при введении второго измерения для определения функций как геометрии отображений.
А причина спора проста. Насколько связно математик должен представлять главные обобщения, чтобы ответить на вопрос о наблюдаемом мире при тех или иных вычисленных значениях модели этого мира?
Что если синус окажется больше единицы?
Это ведь вопрос того, что значит синус и что значит единица.
И если обобщения этого порядка по сути заучены, знания невозможно применить к ситуации.
Проблема чисто алгебраического подхода в бесцельности. Нет движущего фактора определять именно эти числа. Ценность этих чисел в удобстве. Вы предложили рассмотреть принцип полноты.
Не могу согласиться на счет бесцельности — алгебраические и даже арифметические структуры имеют очень богатое поведение и, на самом деле, довольно жестки. Например, практически в любой формальной системе у вас будут аксиомы Пеано, соответственно будут простые числа — это настолько самодостаточная и богатая структура, что ее, имхо, будут изучать вечно.
В этом смысле действительные числа тоже уникальны — это единственное линейно-упорядоченное поле, в котором существуют все пределы. И комплексные, как их алгебраическое замыкание — тоже уникальны. Еще с алгебраической точки зрения, комплексные числа уникальны тем, что это самая сложная коммутативная алгебра с делением.
Опять же, e важно тем, что оно позволяет сконструировать спектр дифференциальных операторов, pi тем, что exp(i*pi) = -1 и т.п.
Я к тому, что все эти вещи берутся действительно не с потолка.
Да, действительно, можно получить больше вещественных чисел с помощью пределов. Доказано ли, что все?
Таким образом можно получить топологически полное пространство со структурой поля, обладающее всеми свойствами, которые мы обычно хотим от точек геометрической прямой. Конечно, мы можем расширять дальше, добавляя всякие странные числа типа гиперреальных.
Топологию можно формально ввести без метрик, да. Но без введения метрик эта топология неаналитична.
Фишка в том, что «решеточная» процедура определения пределов, которую я описал, сама по себе индуцирует стандартную метрику на R, то есть, такая метрика опять же является выделенной — мы ее не вводим, а она получается сама.
А топология без метрики вводится весьма часто. Хороший пример — топология Зарисского.
3. Реальна ли в принципе алгебра без геометрических методов (т.е. без определения геометрических свойствих как расстояние) при введении второго измерения для определения функций как геометрии отображений.
Алгебра может быть как сама по себе, так и с геометрией. Геометрия тоже. Правда союз весьма продуктивен. Вы, наверное, удивитесь, если узнаете, насколько интенсивно используется геометрия в, например, теории чисел.
Важно, чтобы было понимание общей картины. Без понимания того, откуда что берется и зачем оно нужно весьма сложно.
PS: arcsin(2) = Pi/2 — i*log(2 + sqrt(3))
2. Можно ли ввести функции без определения топологии отображения и разделения множеств на непересекающиеся.
У понятия функции вполне конкретное определение. Никакой топологии в нем нет. Функции из A в B определяются в не зависимости от того, пересекаются множества A и B или не пересекаются. В математике постоянно встречается ситуация, когда A и B совпадают. Действительные функции от одной переменной к примеру.
Вещественные числа не непрерывны… Между ними гиперреальные понатыканы в бесконечных количествах
Кто минусует? Имейте смелость признаться.
Вот мой комментарий:
сумма это ряда — да, равна (3.1415...)^2/6 всегда (как вы и утверждаете).
Но!
То, что сумма этого ряда в любых метриках равна (Pi*)^2/6 — возможно, неверно.
Где Pi* — отношения длины окружности к диаметру в каком-нибудь другом пр-ве с другой метрикой.
Что именно используется для выведения этого св-ва?
Вот, например, при выведении формулы Валлиса используется площадь круга.
сумма это ряда — да, равна (3.1415...)^2/6 всегда (как вы и утверждаете).
Но!
То, что сумма этого ряда в любых метриках равна (Pi*)^2/6 — возможно, неверно.
Где Pi* — отношения длины окружности к диаметру в каком-нибудь другом пр-ве с другой метрикой.
Что именно используется для выведения этого св-ва?
Вот, например, при выведении формулы Валлиса используется площадь круга.
Это свойство выводится в рамках аксиоматики Пеано, или любой другой разумной и достаточно сильной аксиоматики (Цермело-Френкеля, Кантора и т.д.)
Я имею в виду, что при выводе этой формулы используется же по существу определение, что Pi — отношение длины окружности к ее диаметру в нашем евклидовом пр-ве (т.е. каноническое определение Pi)?
Вот что я имел в виду.
То есть вопрос был немного другой (связан примерно с тем, о чем мы говорили в другой ветке этой дискуссии), не об аксиоматике.
P.S. Может я вас неправильно понял.
Вот что я имел в виду.
То есть вопрос был немного другой (связан примерно с тем, о чем мы говорили в другой ветке этой дискуссии), не об аксиоматике.
P.S. Может я вас неправильно понял.
undone
Возможно в первую очередь нужно думать в таком духе, что само по себе целое число это нечто совсем иной природы, нежели дробное. В целых числах можно посчитать что-то в штуках. И что было бы если бы пи было равно трем штукам относительно других штук в этом мире?
Математика как раз крайне гибкий и адаптивный инструмент. Мнимые числа дали очень мощный инструмент, хотя все знают, что квадратный корнь из отрицательных чисел не имеет решения в поле вещественных чисел.
Если Вы зададитесь вопросом искривления плоскости, то найдете решение искривления, для которого пи будет равно трем. Это не самая сложная геометрическая задача.
Если Вы зададитесь вопросом искривления плоскости, то найдете решение искривления, для которого пи будет равно трем. Это не самая сложная геометрическая задача.
Только проблема в том, что пи определяется не на абы-какой окружности, а на окружности в R^2 со стандартной метрикой.
Мы же ищем способ так искривить пространство, чтобы не изменив топологию для любой окружности в этом пространстве получить отношение длины к диаметру равное трем. Никто не говорит, что кривизна должна быть постоянной и, более того, статичной. Весь вопрос в том, чем является точка в пространстве.
Но я и правда ошибся. Задача тривиальна только для конкретной окружности.
Однако я и рассматриваю центрированный в наблюдателе мир. То есть измерения делает некий точечный наблюдатель и он всегда восринимает лишь направление на топологической поверхности
Ведь вопрос можно сформулировать так: каким увидит мир наблюдатель, выяснивший, что вего мире значение пи равно трем
Но я и правда ошибся. Задача тривиальна только для конкретной окружности.
Однако я и рассматриваю центрированный в наблюдателе мир. То есть измерения делает некий точечный наблюдатель и он всегда восринимает лишь направление на топологической поверхности
Ведь вопрос можно сформулировать так: каким увидит мир наблюдатель, выяснивший, что вего мире значение пи равно трем
Есть два нюанса — первый заключается в том, что речь шла изначально не об окружностях, а о пи, а у него есть несколько взаимозаменяемых общепринятых определений и то, которое вы пытаетесь использовать, в них не входит. Конечно, можно использовать любое другое, нравящееся вам, определение, но если бы математики так делали, то дальше примитивных понятийных споров бы ничего не продвинулось.
Второй нюанс следующий — евклидова метрика в некотором смысле универсальна, так как локально любое гладкое многообразие является евклидовым (касательное пространство — всегда R^n), поэтому, если вы хотите определять какие-то универсальные константы, то, наверное, имеет смысл это все-таки сделать в R^n.
Второй нюанс следующий — евклидова метрика в некотором смысле универсальна, так как локально любое гладкое многообразие является евклидовым (касательное пространство — всегда R^n), поэтому, если вы хотите определять какие-то универсальные константы, то, наверное, имеет смысл это все-таки сделать в R^n.
Во-первых, нет, такое искривление вы не найдёте. Если рассматривать гладкие двумерные многообразия, то максимум, чего вы можете добиться — это чтобы длина всех окружностей с некоторым фиксированным радиусом r0 была равна 3*r0. Но если устремить радиус к нулю, то отношение длины окружности к радиусу устремится к пи.
Во-вторых, из того, что вы нашли странное пространство, в котором какая-то характеристика равна 3, ещё не следует что вы можете назвать эту константу pi. Пи — это вполне определённая константа, а не свойство произвольно выбранного пространства. Помимо геометрических свойств, она вылезает в анализе, теории чисел и многих других областях математики.
Во-вторых, из того, что вы нашли странное пространство, в котором какая-то характеристика равна 3, ещё не следует что вы можете назвать эту константу pi. Пи — это вполне определённая константа, а не свойство произвольно выбранного пространства. Помимо геометрических свойств, она вылезает в анализе, теории чисел и многих других областях математики.
Вы не рассматриваете гладкие самоподобные преобразования, верно? Только монотонные?
Эээ… Я про преобразования не говорил, я говорил в терминах гладких многообразий.
Вопрос к тому, что Вы по факту уходите в сложившуюся терминологию не вдаваясь в то, зачем она так сложилась. Не буду дальше дискутировать, чтобы не портить себе репутацию минусами тех, кто не понимает сказанного, но общий смысл заключен в том, что евклидовы метрики как раз всего лишь хорошо формализованы, но это вовсе не значит, что не найдется фрактальной метрики, формализация которой окажется более тривиальной и сложные задачи окажутся простыми.
Математика это не только применение уже известных свойств, но и выведение новых. А дЛя выведения новых нужно хорошо понимать, где введенные ограничения связаны лишь с трудностью вычислений.
Фрактальные метрики это весьма перспективная тема. И неизбитая и необходимая. Мы же знаем, что пространство неоднородно. А какова природа этой неоднородности сказать не можем.
Математика отнюдь не пострадает от исследований комплекснозначных метрик. Это не говоря еще об обобщениях, ведь топология — не единственное возможное обобщение метрики
Математика это не только применение уже известных свойств, но и выведение новых. А дЛя выведения новых нужно хорошо понимать, где введенные ограничения связаны лишь с трудностью вычислений.
Фрактальные метрики это весьма перспективная тема. И неизбитая и необходимая. Мы же знаем, что пространство неоднородно. А какова природа этой неоднородности сказать не можем.
Математика отнюдь не пострадает от исследований комплекснозначных метрик. Это не говоря еще об обобщениях, ведь топология — не единственное возможное обобщение метрики
Я не против новых абстракций. Я лишь против того, чтобы вот так прямо представлять пространство с другим пи. Даже если ограничиться определением пи как отношения длины окружности к диаметру, пространство, в котором оно будет постоянным и отличным от 3.14… будет настолько математически отличным от нашего, что говорить о его «физических» свойствах бессмысленно.
Если говорить о наиболее существенном определении числа пи, то тут есть глубочайшая философская проблема.
Первая часть этой проблемы заключается в том, что человек воспринимает мир как результат электромагнитного взаимодействия. По этой причине мир воспринимается трехмерным. И В этом смысле число пи это просто проекция фронта любой электромагнитной волны во времени на воображаемую бесконечно удаленную вечную сферу. То есть это топология восприятия, не более того.
Вторая часть этой проблемы заключена в том, что человек дав одно определение вынужден строить модель определений, ограниченную этим первым. И если исходить из определения признаков и обобщений чисто топологически, то первый признак это точка, второй -различение двух точек как разных, третий — различение относительных расстояний между двумя точками, четвертый различение изменчивости расстояний и т.п.
То есть по факту, трехмерность мира это вопрос уже достаточно развитых обобщений, исходная же топология безмерна.
Вы же оперируя следствиями пытаетесь судить дажене о причинах, а о самом характере причин.
Первая часть этой проблемы заключается в том, что человек воспринимает мир как результат электромагнитного взаимодействия. По этой причине мир воспринимается трехмерным. И В этом смысле число пи это просто проекция фронта любой электромагнитной волны во времени на воображаемую бесконечно удаленную вечную сферу. То есть это топология восприятия, не более того.
Вторая часть этой проблемы заключена в том, что человек дав одно определение вынужден строить модель определений, ограниченную этим первым. И если исходить из определения признаков и обобщений чисто топологически, то первый признак это точка, второй -различение двух точек как разных, третий — различение относительных расстояний между двумя точками, четвертый различение изменчивости расстояний и т.п.
То есть по факту, трехмерность мира это вопрос уже достаточно развитых обобщений, исходная же топология безмерна.
Вы же оперируя следствиями пытаетесь судить дажене о причинах, а о самом характере причин.
Вот интересно все же, тот кто минусанул, понимает, о чем речь? Или так, по праву большего рейтинга? Стыдобища.
>По этой причине мир воспринимается трехмерным.
Как получается этот вывод?
Как получается этот вывод?
Можете порекомендовать литературу по первой части проблемы?
Я вот смотрю на этот спор и удивляюсь. Хотя тут спорить вообще не о чем. Канонически число Пи определяется через e2pi=1. И это выражение не подвержено никаким топологическим и геометрическим трансформациям. Соответственно, оба числа e и pi неизменны при любом раскладе — просто потому, что математика такова — это базовые концепции.
Соответственно, как бы ни усирался интервьюер в своем упорстве узнать, что случится, если число Пи будет иметь другое значение, можно ответить просто и однозначно: число Пи не может быть другим в этом его подлинно арифметическом смысле. Это просто невозможно. То есть любые потуги интервьюера намекнуть о другом значении числа Пи говорят о его полной математической безграмотности. Посудите сами, давайте тогда пофантазируем, что будет если число e будет не 2.718…, а, например, 2. Сие есть бред чистой воды, к математике никакого отношения не имеющий.
Далее интересный момент. В наблюдаемом мире арифметическое значение числа Пи совпадает с геометрическим значением, вычисляемым по известному отношению длины окружности к ее радиусу для нашего плоского пространства Минковского. Вот это все уже имеет отношение как раз к геометрии/топологии. Да, в неевклидовой геометрии и связанных с ней топологических пространствах это отношение (длины окружности к ее радиусу) может быть другим, не равным каноническому Пи. И в этом есть одновременно загадка, но и решение некоторых проблем Космологии. Почему эти числа совпадают в нашем пространстве, почему мы находимся в таком исключительном выделенном пространстве?
Я не более месяца назад читал препринт по теор.физике. Смысл там такой: на деле все указывает на то, что наше пространство все же неевклидово. Но для тех, кто находится внутри пространства, геометрия всегда будет равна геометрии плоского пространства Минковского. причем, только по той причине, что такова математика и выражение e2pi=1 будет всегда верно. Такой вот всеобъемлющий закон природы. Мы просто обязаны воспринимать наше пространство плоским, потому что иначе невозможна классическая алгебра, что есть фундамент математики и, соответственно, геометрии, топологии и прочая прочая. Виртуально мы можем придумать любое пространство и описывать его как нам удобно, но фактическим пространством, где мы находимся, может быть только плоское пространство. Иначе полный крэш.
Из этого вытекает, что реально нет никакой лямбды в уравнениях Эйнштейна. Нет никакой темной энергии, нет того статического поля, привносящего отрицательную энергию, дающую отталкивание. Есть лишь искривление нашего пространства, и надо произвести преобразования из одного пространства в другое, учитывая ту лямбду. Так мы получим реальную конфигурацию нашего пространства. И у этого подхода уйма последствий, вплоть до объяснения почему скорость света именно такая, а не другая, и почему разного рода физические константы именно такие. И эта реальная кривизна зависит от расширения Вселенной, и даже от ее возраста. То есть она меняется. Также там есть свои интересные моменты в описании гравитации, почему тела притягиваются. В общем, это такая новая продуктивная тема для исседований. А всё только лишь из-за двух чисел pi и e. Получается, что математика не просто описывает Вселенную, а сама математика действительно лежит в основе Вселенной. По мне — абсолютная красота.
Соответственно, как бы ни усирался интервьюер в своем упорстве узнать, что случится, если число Пи будет иметь другое значение, можно ответить просто и однозначно: число Пи не может быть другим в этом его подлинно арифметическом смысле. Это просто невозможно. То есть любые потуги интервьюера намекнуть о другом значении числа Пи говорят о его полной математической безграмотности. Посудите сами, давайте тогда пофантазируем, что будет если число e будет не 2.718…, а, например, 2. Сие есть бред чистой воды, к математике никакого отношения не имеющий.
Далее интересный момент. В наблюдаемом мире арифметическое значение числа Пи совпадает с геометрическим значением, вычисляемым по известному отношению длины окружности к ее радиусу для нашего плоского пространства Минковского. Вот это все уже имеет отношение как раз к геометрии/топологии. Да, в неевклидовой геометрии и связанных с ней топологических пространствах это отношение (длины окружности к ее радиусу) может быть другим, не равным каноническому Пи. И в этом есть одновременно загадка, но и решение некоторых проблем Космологии. Почему эти числа совпадают в нашем пространстве, почему мы находимся в таком исключительном выделенном пространстве?
Я не более месяца назад читал препринт по теор.физике. Смысл там такой: на деле все указывает на то, что наше пространство все же неевклидово. Но для тех, кто находится внутри пространства, геометрия всегда будет равна геометрии плоского пространства Минковского. причем, только по той причине, что такова математика и выражение e2pi=1 будет всегда верно. Такой вот всеобъемлющий закон природы. Мы просто обязаны воспринимать наше пространство плоским, потому что иначе невозможна классическая алгебра, что есть фундамент математики и, соответственно, геометрии, топологии и прочая прочая. Виртуально мы можем придумать любое пространство и описывать его как нам удобно, но фактическим пространством, где мы находимся, может быть только плоское пространство. Иначе полный крэш.
Из этого вытекает, что реально нет никакой лямбды в уравнениях Эйнштейна. Нет никакой темной энергии, нет того статического поля, привносящего отрицательную энергию, дающую отталкивание. Есть лишь искривление нашего пространства, и надо произвести преобразования из одного пространства в другое, учитывая ту лямбду. Так мы получим реальную конфигурацию нашего пространства. И у этого подхода уйма последствий, вплоть до объяснения почему скорость света именно такая, а не другая, и почему разного рода физические константы именно такие. И эта реальная кривизна зависит от расширения Вселенной, и даже от ее возраста. То есть она меняется. Также там есть свои интересные моменты в описании гравитации, почему тела притягиваются. В общем, это такая новая продуктивная тема для исседований. А всё только лишь из-за двух чисел pi и e. Получается, что математика не просто описывает Вселенную, а сама математика действительно лежит в основе Вселенной. По мне — абсолютная красота.
А можно вопрос?
Вот смотрите, у нас есть, допустим, два определения Pi.
Определение 1 -геометрическое в нашем евклидовом пр-ве.
Определение 2 — через сумму ряда (или произведение)
При этом определение №1 является первичным (по крайней мере, с т.з. истории).
У нас получается, что в нашем евклидовом пр-ве числа, определенные 1-м и 2-м способом, совпадают и равны 3.1415..., но
для какого-то другого про-ва возможно ли, что определение №1 в нем приводит в другой константе (допустим, 3), а определение через ряд остается равным 3.1415....?
Таким образом, если мы зафиксируем для Pi именно определение №1, а не через сумму ряда, то оно может меняться от пр-ва к пр-ву?
Вот смотрите, у нас есть, допустим, два определения Pi.
Определение 1 -геометрическое в нашем евклидовом пр-ве.
Определение 2 — через сумму ряда (или произведение)
При этом определение №1 является первичным (по крайней мере, с т.з. истории).
У нас получается, что в нашем евклидовом пр-ве числа, определенные 1-м и 2-м способом, совпадают и равны 3.1415..., но
для какого-то другого про-ва возможно ли, что определение №1 в нем приводит в другой константе (допустим, 3), а определение через ряд остается равным 3.1415....?
Таким образом, если мы зафиксируем для Pi именно определение №1, а не через сумму ряда, то оно может меняться от пр-ва к пр-ву?
[Терминологическая придирка] Если пространство евклидово, то число пи в нём будет какое надо.
По существу. Если мы рассмотрим искривлённое пространство, в котором отношение длины окружности к диаметру не будет равно пи, то в любом «нормальном» случае у разных окружностей это отношение будет разным. Дело в том, что гладкие пространства в малой окрестности любой точки должны хорошо приближаться евклидовым пространством, соответственно, для маленьких окружностей отношение длины к диаметру будет близко к pi. При этом нормальное опредление длины кривой, если я не ошибаюсь, у нас есть только для гладких пространств.
Я не готов с уверенностью утверждать, что в принципе невозможно придумать пространство в котором длины всех окружностей будут в 3 раза больше их диаметра, но в любом случае даже если это возможно, получившееся пространство будет не очень полезным, типа вашего пространства, в котором большой шар лежит в малом.
По существу. Если мы рассмотрим искривлённое пространство, в котором отношение длины окружности к диаметру не будет равно пи, то в любом «нормальном» случае у разных окружностей это отношение будет разным. Дело в том, что гладкие пространства в малой окрестности любой точки должны хорошо приближаться евклидовым пространством, соответственно, для маленьких окружностей отношение длины к диаметру будет близко к pi. При этом нормальное опредление длины кривой, если я не ошибаюсь, у нас есть только для гладких пространств.
Я не готов с уверенностью утверждать, что в принципе невозможно придумать пространство в котором длины всех окружностей будут в 3 раза больше их диаметра, но в любом случае даже если это возможно, получившееся пространство будет не очень полезным, типа вашего пространства, в котором большой шар лежит в малом.
Я вас примерно понял (вернее будет сказать немного понял)
На самом деле очень интересно, что за страшным потоком формул и разных непонятных конструкций скрываются вещи, которые можно объяснить если не на доступном языке, то хотя бы доступно с некоторым уровнем упрощения.
P.S. Если честно, в свое время дифгем вообще мимо ушей пропустил :(
На самом деле очень интересно, что за страшным потоком формул и разных непонятных конструкций скрываются вещи, которые можно объяснить если не на доступном языке, то хотя бы доступно с некоторым уровнем упрощения.
P.S. Если честно, в свое время дифгем вообще мимо ушей пропустил :(
Я вижу, вы умный человек с сильным математическим образованием.
Скажите откровенно, насколько ваши знания, которые вы получили в университете, пригодились вам на работе?
Если можно оценить в процентах (примерно, хотя бы диапазон).
Если нельзя — то как-то неформально, но чтобы была какая-то интересная информация.
Скажите откровенно, насколько ваши знания, которые вы получили в университете, пригодились вам на работе?
Если можно оценить в процентах (примерно, хотя бы диапазон).
Если нельзя — то как-то неформально, но чтобы была какая-то интересная информация.
Спасибо за комплимент.
Я учился на матмехе СПбГУ и работаю программистом в Google. Из полученных знаний хоть как-то полезны процентов 30, может быть. Темы связанные с computer science у нас были на спецкурсах, но и помимо них есть анализ, линейная алгебра, комбинаторика, теорвер — все эти дисциплины вполне релевантны.
Хотя, конечно, будь моя воля, я бы сейчас по-другому построил своё обучение.
Я учился на матмехе СПбГУ и работаю программистом в Google. Из полученных знаний хоть как-то полезны процентов 30, может быть. Темы связанные с computer science у нас были на спецкурсах, но и помимо них есть анализ, линейная алгебра, комбинаторика, теорвер — все эти дисциплины вполне релевантны.
Хотя, конечно, будь моя воля, я бы сейчас по-другому построил своё обучение.
Ну то есть все тополого-геометрические знания не требуются особо?
А в какой степени линейная алгебра, анализ и теорвер востребованы?
Теорвер же может быть достаточно абстрактный и загруженный, если изучать со всякими борелевскими сигма-алгебрами, интегралами Лебега и т.п.?
Анализ 4-ый семестр идет что-то типа поверхностных и двойных интегралов, тоже, наверное, не используется на работе?
Фактически из математики используется то, что давали на 1-1.5 курсах, плюс теорвер и дискретная математика?
Ну 30% — это еще неплохой показатель, как мне кажется, для программиста.
А в какой степени линейная алгебра, анализ и теорвер востребованы?
Теорвер же может быть достаточно абстрактный и загруженный, если изучать со всякими борелевскими сигма-алгебрами, интегралами Лебега и т.п.?
Анализ 4-ый семестр идет что-то типа поверхностных и двойных интегралов, тоже, наверное, не используется на работе?
Фактически из математики используется то, что давали на 1-1.5 курсах, плюс теорвер и дискретная математика?
Ну 30% — это еще неплохой показатель, как мне кажется, для программиста.
С топологией я как-то не сталкивался.
Линейная алгебра используется, к примеру, во всех оптимизациях. Часто возможные конфигурации рассматриваются как многомерные веркторы, и к чему-нибудь применяется поиск совственных векторов.
Сигма-алгебры не встречаются.
Двойные интегралы могут, наверное, пригодиться в отдельных областях, но вряд ли часто.
Линейная алгебра используется, к примеру, во всех оптимизациях. Часто возможные конфигурации рассматриваются как многомерные веркторы, и к чему-нибудь применяется поиск совственных векторов.
Сигма-алгебры не встречаются.
Двойные интегралы могут, наверное, пригодиться в отдельных областях, но вряд ли часто.
Ну понятно, в целом достаточно ограниченное применение математики. Все, что нужно, можно уместить максимум в два года.
Хотя меня всегда поражало, как одни области математики связаны с другими. Та же теория чисел, которая используется в криптографии (и может тоже иметь в программировании), связана с тем же комплексным анализом.
Хотя меня всегда поражало, как одни области математики связаны с другими. Та же теория чисел, которая используется в криптографии (и может тоже иметь в программировании), связана с тем же комплексным анализом.
Комплексный анализ нужен также для преобразований Фурье, которые в программировании вполне встречаются.
Скорее, в 4 года. В лучшем случае, 3.5. Остальные полтора-два года потратить на углублённое изучение того, что заинтересовало. Не забывайте про численные методы — это ещё год довольно плотного изучения, а знать их надо хотя бы на уровне «как и почему это работает».
Абстрактная топология не требуется, хотя иногда приходится анализировать всякие сходимости (в том числе, функциональных рядов). Геометрию использую на 146% от университетского курса, правда, большей частью для развлечения — для личных проектов. Но и в работе наглядно представлять траектории и проекции в «600-мерном пространстве» иногда приходится (и начальник, кажется, понимает, что я имею в виду). Теория меры и интеграл Лебега — вряд ли. Поверхностные интегралы, криволинейные преобразования пространств, нетривиальная топология — используются довольно часто. Теория чисел (та, где конечные поля) — тоже.
Скажите откровенно, насколько ваши знания, которые вы получили в университете, пригодились вам на работе?
У меня тоже получается процентов 30. Возможно, чуть больше (40-45). Думаю, что это достаточно много — никогда не знаешь, что именно пригодится в дальнейшем, и неплохо бы, чтобы потенциально полезные знания были под рукой. Сложись жизнь чуть иначе — востребованными оказались бы не комплексные числа и рациональные функции, а какие-нибудь уравнения в частных производных и квантовая физика.
Аргументация к авторитету. Неубедительно.
А зачем им быть гладкими? Сядьте в вершину конуса с подходящим углом при вершине, и отношение длины окружности к диаметру будет всегда равно 3. Если вы — существо трёхмерное, возьмите сферический конус в 4D. Правда, чтобы потом уйти из этой вершины, нужно очень гибкое тело, как у амёбы или осьминога — иначе можно порезаться. Но это дело техники, в неоднородных пространствах твёрдые тела, скорее всего, не будут существовать (хотя земляне как-то существуют, несмотря на гравитационное искривление?)
На конусе этим свойством будут обладать только окружности с центром в вершине.
А я не спорю. Но любые такие окружности.
Можно добавить больше вершин. У окружностей длиной 6R будет ограничен радиус, зато возможных центров станет больше.
Можно добавить больше вершин. У окружностей длиной 6R будет ограничен радиус, зато возможных центров станет больше.
И что доказывает этот пример? Будет несколько семейств окружностей с таким свойством. Возвращаясь к исходному вопросу, это как-то скажется на значении пи? Нельзя даже утверждать, что мы нашли пример пространства где все окружности такие.
Хорошо. Хотите, чтобы все окружности были такими — возьмите плоскость с 6-угольными кругами:
dist((0,0),(x,y))=max(|x|+|y|/sqrt(3),|y|*2/sqrt(3)).
Повороты останутся только на 60 градусов, некоторые отрезки превратятся в параллелограммы. Но длина каждой окружности будет ровно 6*R, независимо от центра и радиуса. На остальную математику — наплевать, кому она нужна…
А если взять метрику L_1 или L_\infty, то там длина окружности будет 8*R. И этот пример тоже ничего не доказывает.
dist((0,0),(x,y))=max(|x|+|y|/sqrt(3),|y|*2/sqrt(3)).
Повороты останутся только на 60 градусов, некоторые отрезки превратятся в параллелограммы. Но длина каждой окружности будет ровно 6*R, независимо от центра и радиуса. На остальную математику — наплевать, кому она нужна…
А если взять метрику L_1 или L_\infty, то там длина окружности будет 8*R. И этот пример тоже ничего не доказывает.
Да, согласен, это хороший пример. С физикой на таком пространстве, правда, могут возникнуть проблемы, по крайней мере нашу физику на него будет перенести сложно.
Можно уточняющий вопрос?
Как вы в таком пространстве считаете длину окружности (т.е. фактически шестиугольника)?
То есть как нам получить, что длина одной стороны этого шестиугольного круга равна R?
Мне понятно, как посчитать расстояние от одной точки до любой другой, распространив вашу формулу следующим образом:
dist((x1,y1),(x2,y2))=max(|x1-x2|+|y1-y2|/sqrt(3),|y1-y2|*2/sqrt(3))
Но как посчитать длину кривой в этой метрике?
Да, это прямые в метрике R2 и там все было бы понятно, но у нас-то другая метрика.
Как вы в таком пространстве считаете длину окружности (т.е. фактически шестиугольника)?
То есть как нам получить, что длина одной стороны этого шестиугольного круга равна R?
Мне понятно, как посчитать расстояние от одной точки до любой другой, распространив вашу формулу следующим образом:
dist((x1,y1),(x2,y2))=max(|x1-x2|+|y1-y2|/sqrt(3),|y1-y2|*2/sqrt(3))
Но как посчитать длину кривой в этой метрике?
Да, это прямые в метрике R2 и там все было бы понятно, но у нас-то другая метрика.
Любой отрезок в L2 остаётся подмножеством отрезка и в «многоугольных» метриках. Сторона шестиугольника идёт в том же направлении, что и направление от центра к вершине (и длина его такая же), так что длина этой стороны действительно равна R. То есть, ответ на вопрос «как нам получить» — перенести сторону так, чтобы одна вершина оказалась в центре. Тогда вторая окажется точно на «окружности» (в вершине шестиугольника), то есть её длина будет как раз R.
Любой отрезок в L2 остаётся подмножеством отрезка и в «многоугольных» метриках.
Да, вот примерно это я и хотел узнать, т.к. дальнейшие рассуждения примерно понятны.
Ведь только в определенных случаях (а именно, в случаях отрезка) мы можем вычислить длину кривой (в нашем случае — отрезка) как расстояние между его крайними точками. Так?
Мне просто было интересно, не может ли произойти такого, что при переходе из одной метрики в другую отрезки в первой метрике перестают быть отрезками во второй метрике?
Кстати, что такое «отрезок» или «прямая» в произвольном метрическом пр-ве? Это же понятие не всегда будет определено? В отличие, скажем, от шара или сферы?
Да, вот примерно это я и хотел узнать, т.к. дальнейшие рассуждения примерно понятны.
Ведь только в определенных случаях (а именно, в случаях отрезка) мы можем вычислить длину кривой (в нашем случае — отрезка) как расстояние между его крайними точками. Так?
Мне просто было интересно, не может ли произойти такого, что при переходе из одной метрики в другую отрезки в первой метрике перестают быть отрезками во второй метрике?
Кстати, что такое «отрезок» или «прямая» в произвольном метрическом пр-ве? Это же понятие не всегда будет определено? В отличие, скажем, от шара или сферы?
Что вообще такое отрезок?
Правильно ли определить отрезок так, что это множество точек с двумя выделенными точками А и B, такими, что для любой другой точки C из этого множества неравенство треугольника обращается в строгое равенство, то есть:
d(A,B)=d(A,C)+d(C,B)
Правильно ли определить отрезок так, что это множество точек с двумя выделенными точками А и B, такими, что для любой другой точки C из этого множества неравенство треугольника обращается в строгое равенство, то есть:
d(A,B)=d(A,C)+d(C,B)
Да, есть такое определение. В некоторых случаях отрезки выглядят нормально, как кусочки геодезических. В других — становятся толстыми, например, параллелограммами. Это когда «окружность» имеет прямые (в обычном смысле) участки. А иногда от отрезка остаются только начало и конец. Например, если мы определим метрику на сфере как декартово (трёхмерное) расстояние между точками. Тоннель со сферой почти не пересекается :)
Число Пи является константой в Эвклидовой геометрии, которая приближена к реальности по свойствам.
Однако, например, можно задать геометрию на плоскости сферы — тогда отношение диаметра к длине окружности уже не будет равным Пи.
Соответственно, вопрос «что будет, если Pi = 3» можно трактовать, как «как бы выглядело пространство (и соответствующая ему выдуманная физическая вселенная), в котором бы Pi = 3».
Однако, например, можно задать геометрию на плоскости сферы — тогда отношение диаметра к длине окружности уже не будет равным Пи.
Соответственно, вопрос «что будет, если Pi = 3» можно трактовать, как «как бы выглядело пространство (и соответствующая ему выдуманная физическая вселенная), в котором бы Pi = 3».
1. Число пи появляется в математике в тысяче мест и помимо евклидовой геометрии. Некоторые из них я в комментариях уже привёл.
2. На сфере отношение длины окружности к диаметру будет разным для разных окружностей, и при радиусе стремящемся к 0 будет стремиться к тому же pi. Этот же факт будет верен для всех других гладких поверхностей.
3. Такое пространство практически невозможно.
2. На сфере отношение длины окружности к диаметру будет разным для разных окружностей, и при радиусе стремящемся к 0 будет стремиться к тому же pi. Этот же факт будет верен для всех других гладких поверхностей.
3. Такое пространство практически невозможно.
Число пи появляется в математике в тысяче мест и помимо евклидовой геометрии.
То, что оно появляется в тысяче мест — это итак понятно. Это объясняется свойствами этого числа, исходящими из его определения: отношение длины окружности к диаметру, а также тем, что все сводится к банальным пространствам, вроде (x, y, z), где можно выделить обычные плоскости, т.е. можно любое искривленное пространство или его подпространства выразить через традиционные понятия, где наше Пи будет иметь место.
Кроме того, мнимые числа тоже выражают плоское двумерное пространство, где применимы тригонометрические операции, т.е. где применимы мнимые числа, там может возникнуть и Пи, грубо говоря.
На сфере отношение длины окружности к диаметру будет разным для разных окружностей, и при радиусе стремящемся к 0 будет стремиться к тому же pi. Этот же факт будет верен для всех других гладких поверхностей.
Я не спорю. Я лишь привел пример пространства и геометрии, основанной на этом пространстве, где отношение длины окружности к диаметру отличается от обычного значения Пи.
Такое пространство практически невозможно.
Это если мы рассматриваем непрерывное гладкое пространство.
А вопрос сводится именно к тому, чтобы оценить свойства и примерно предстваить пространство, где отношение длин окружностей к диаметрам всегда равно трем.
Понятно, что оно не будет евклидовым и, кроме того, будет иметь крайне необычные свойства — дырки, «порталы», вырвиглазную многомерность, неоднородность длин или что еще похуже.
Например, я могу дать такое определение некоего пространства с метрикой: в этом пространстве длины всех окружностей равны трем, а их диаметры — единице. Оно будет отвечать условиям вопроса.
Свойства этого пространства могут казаться парадоксальными, но, например, свойства геометрии Лобачевского тоже выглядят парадоксальными с точки зрения Евклидовой.
Я где-то там выше в комментариях написал уже один раз длинную телегу о том, как получается число пи ну вообще безо всякой евклидовой геометрии. В частности и про то, что комплексные числа изначально не из геометрических соображений появились.
Пример пространства с другой длинной окружности здесь где-то уже привели — просто берём норму L1 вместо L2 — и отношение длины окружности к радиусу становится равно 4. Без всяких вырвиглазных свойств. Но на это пространство не «натягивается» наша традиционная физика, так что говорить о том, что будет, если у нас пи внезапно станет равно 3-м не приходится.
Пример пространства с другой длинной окружности здесь где-то уже привели — просто берём норму L1 вместо L2 — и отношение длины окружности к радиусу становится равно 4. Без всяких вырвиглазных свойств. Но на это пространство не «натягивается» наша традиционная физика, так что говорить о том, что будет, если у нас пи внезапно станет равно 3-м не приходится.
Отношение будет не 4, а 8. В пространстве L1 pi=4 (насколько я понимаю, это максимально возможное его значение). Минимальное — как раз 3. Но это то pi, которое используется в остальной математике.
Я где-то там выше в комментариях написал уже один раз длинную телегу о том, как получается число пи ну вообще безо всякой евклидовой геометрии. В частности и про то, что комплексные числа изначально не из геометрических соображений появились.
Если мы получаем число Пи вне Евклидовой геометрии — это означает, что мы проводим манипуляции, которые имеют геометрический смысл, который в том или ином виде сводится к делению длины некоторой окружности к ее диаметру.
В частности, например, выражение sin/cos через экспоненту с мнимыми степенями/коэффициентами — это следствие того, что мнимые числа можно выразить через точки на двухмерной плоскости, с соответствующими последствиями.
Иными словами, в самом числе Пи нет никакого божственного промысла. Если мы получили это значение каким-либо способом, то значит наши преобразования можно выразить геометрически, сводя все к определению значения Пи.
Но на это пространство не «натягивается» наша традиционная физика, так что говорить о том, что будет, если у нас пи внезапно станет равно 3-м не приходится.
Конечно не «натягивается». Наша физика строится на мире, где априори применима только Евклидова геометрия.
И если мы выдумываем мир в неевклидово пространстве, то все, что мы можем — только «подогнать» некоторые свойства вселенной максимально близо к нашим (различные коэффициенты, константы), где это возможно, не ломая целостность придуманного пространства.
Поэтому я и привел свою трактовку вопроса, которая мне кажется более корректной: как бы выглядело пространство (и соответствующая ему выдуманная физическая вселенная), в котором бы Pi = 3.
Речи о нашей вселенной, как вы видите, даже и нет.
Если мы получаем число Пи вне Евклидовой геометрии — это означает, что мы проводим манипуляции, которые имеют геометрический смысл, который в том или ином виде сводится к делению длины некоторой окружности к ее диаметру.
И какой же геометрический смысл имеет определение pi как наименьшего положительного x: f(x)=0, где f(x)+(d2f/dx2)(x)=0, f(0)=0, (df/dx)(0)=2?
Или как суммы ряда 4/1-4/3+4/5-4/7+...?
И какой же геометрический смысл имеет определение pi как наименьшего положительного x: f(x)=0, где f(x)+(d2f/dx2)(x)=0, f(0)=0, (df/dx)(0)=2?
Подставьте вместо f(x) — sin(x) и смысл, я думаю, вам будет понятен.
Иными словами, множество функций, удовлетворяющих этим свойствам, выражаются тем или иным образом через тригонометрические функции.
(UPD: возможно, sin(x) здесь не лучший пример, т.к. я не учел (df/dx)(0)=2, но это не отменяет моего утверждения о сводимости к тригонометрическим функциям.)
Или как суммы ряда 4/1-4/3+4/5-4/7+...?
Это ряд Мадхавы-Лейбница, который является, по сути, «умноженным на 4» рядом Лейбница. Собственно, сам ряд Лейбница можно получить из разложения арктангенса 1 в ряд Тейлора.
Источник: http://ru.wikipedia.org/wiki/%D0%A0%D1%8F%D0%B4_%D0%9B%D0%B5%D0%B9%D0%B1%D0%BD%D0%B8%D1%86%D0%B0
Во-первых, не sin(x), а 2*sin(x). Во-вторых, вам как-то геометрически придётся доказать, что вторая производная по углу отношения катета к гипотенузе ведёт себя нужным образом (не обращаясь к матанализу!), и объяснить геометрический смысл ряда Тейлора (который сам по себе к геометрии тоже не относится) — и доказать (опять же, геометрически), что у арктангенса он именно такой. Иначе получится, что вы с помощью математики провели кучу выкладок, и только после них получили удобный вам результат, который можно интерпретировать в терминах евклидовой геометрии.
Во-первых, не sin(x), а 2*sin(x).
Да, про sin(x) да, я уже сделал UPD.
Во-вторых, вам как-то геометрически придётся доказать, что вторая производная по углу отношения к… (пока не буду приводить всю цитату)
Вы уже занимаетесь софистикой.
Во-первых, я свел ваши примеры к тригонометрическим функциям.
Во-вторых, очевидно, что тригонометрические функции имеют геометрический смысл (не просто геометрический, а связанный с окружностями — это важно), как и операции с ними.
В-третьих, из первого и второго следует, что приведенные вами выражения можно преобразовать в выражения, геометрический смысл которых очевиден (если нет, то я могу его вам привести).
Но, тем не менее, если вы так этого просите, пытаясь меня убедить, что число Пи имеет какое-то сверхестественное значение вне его исходного опоределения, то тогда пожалуйста:
Во-вторых, вам как-то геометрически придётся доказать, что вторая производная по углу отношения катета к гипотенузе ведёт себя нужным образом (не обращаясь к матанализу!)
Начнем с того, что мы имеем некоторый математический аппарат на множестве вещественных чисел, которое имеет 1-1 соответствие с некоторым множеством отрезков различной длины в евклидовом пространстве.
Начнем с того, что sin/cos имеют не просто геометрический смысл, а также можно выразить длиной некоторого отрезка: мы рисуем оси x и y, проводим единичную окружность от центра координат, и рисуем прямую под углом фи от оси x. От точки пересечения прямой и коружности проводим перпендикуляр к оси x — получаем отрезок, соответствующий значению sin(фи).
Далее, очевидно, что все операции над полем вещественных чисел имеют свои геометрические аналоги (сложение, умножение, деление преобразуются в аналогичные операции над отрезками).
Далее, вспомним определение производной, который в том или ином виде сводится к некоему пределу некоторых операций над полем вещественных чисел, то есть можно все это свести к операциям над отрезками.
Хотя, чего мы вообще возимся с этим полем вещественных чисел?
Взаимнооднозначное соответствие поля Вещественных числе и некоторого поля конечных отрезков очевидна.
Таким образом наша вся математика построена на геометрических отрезках, где мы и определяем и понятия производных и ряды Тейлора и даже доказываем, что ряд Лейбница выводится из ряда Тейлора для арктангенса…
А на самом деле
Надеюсь, вы не сильно обиделись над тем. что я позволил себе поглумиться над вашим комментарием? Ваше утверждение «Иначе получится, что вы с помощью математики провели кучу выкладок, и только после них получили удобный вам результат, который можно интерпретировать в терминах евклидовой геометрии» выглядит, мягко говоря, глупо. В математике нельзя просто взять и получить «удобный результат» из неоткуда. Если выражение сводится к тригонометрическим функциям — это априори означает, что заданное выражение можно геометрически выразить (простите за тафтологию) через соответствующие геометрические сущности. То есть, особая роль числа Пи в таких выражениях теряет свой мистический смысл. Например в функции f(x) = 2*x у числа Пи нет никакого особенного смысла.
Вопрос, как всегда, в том, что первично. Либо мы считаем, что первична и истинна геометрия (причём евклидова), а вещественные числа, операции над ними и функции возникли как попытка «математизировать» эту геометрию, либо наоборот — что первична теория множеств, а натуральный ряд, вещественные числа, геометрия и т.п. — всего лишь частные конструкции над этой теорией (геометрия — только некоторые соотношения между парами или тройками вещественных чисел и их множествами — в конечном итоге, система полиномиальных уравнений). Оба подхода имеют право на существование, оба одинаково неверны. И как определять синус — в конечном итоге, вопрос вкуса. Всё равно определения эквивалентны.
Я не вижу противоречий в том, что вы говорите, просто, возможно, вы не совсем понимаете мой посыл из-за фразы «геометрический смысл».
Поэтому, переформулирую посыл, чтобы он не вызывал лишних вопросов.
Число Пи не имеет никакого особого* значения в математике. Единственное место в математике, где число Пи обладает каким-то особым* смыслом — это тригонометрические функции, т.к. они геометрически выражаются через единичную окружность и, соответственно, углы, выраженные через Пи, создают предсказуемые значения.
Таким образом, отсюда я делаю утверждение, что любое выражение, где Пи имеет «особое*» значение, выражается так или иначе через тригонометрические функции всегда.
*под особым смыслом, подразумевается, что использование Пи в качестве аргумента приводит к какому-нибудь «особому в данном контексте» результату: что-нибудь по аналогии 0 или 1 от синуса/косинуса, или какие-нибудь целые/рациональные значения в функциях, где подобные результаты крайне неочевидны, а то и вообще зачастую трансценденты, если не используется значение, выражаемое через Пи. Так же под особым смыслом подразумевается выражение Пи через какие-либо ряды, вычисления и прочее. Стоит также учитывать, что для любого случайного числа можно создать ряд, который к нему сводится, поэтому, ряд Лейбница выделяется только потому, что в нем нет членов, выражаемых через Пи.
Поэтому, переформулирую посыл, чтобы он не вызывал лишних вопросов.
Число Пи не имеет никакого особого* значения в математике. Единственное место в математике, где число Пи обладает каким-то особым* смыслом — это тригонометрические функции, т.к. они геометрически выражаются через единичную окружность и, соответственно, углы, выраженные через Пи, создают предсказуемые значения.
Таким образом, отсюда я делаю утверждение, что любое выражение, где Пи имеет «особое*» значение, выражается так или иначе через тригонометрические функции всегда.
*под особым смыслом, подразумевается, что использование Пи в качестве аргумента приводит к какому-нибудь «особому в данном контексте» результату: что-нибудь по аналогии 0 или 1 от синуса/косинуса, или какие-нибудь целые/рациональные значения в функциях, где подобные результаты крайне неочевидны, а то и вообще зачастую трансценденты, если не используется значение, выражаемое через Пи. Так же под особым смыслом подразумевается выражение Пи через какие-либо ряды, вычисления и прочее. Стоит также учитывать, что для любого случайного числа можно создать ряд, который к нему сводится, поэтому, ряд Лейбница выделяется только потому, что в нем нет членов, выражаемых через Пи.
То, что пи не имеет «особого значения», я согласен. Оно такое же «особое», как sqrt(3), ln(2), exp(1), C и прочие константы, возникающие в самых разных местах. Более того, pi=ln(-1)/sqrt(-1) (одно из значений). Но почему вы говорите, что оно имеет «особый смысл» именно в геометрии, а не, скажем в теории вероятностей, где оно совершенно непостижимым образом забралось в центральную предельную теорему, и теперь все вынуждены писать это 1/sqrt(2*pi*sigma)?
Но почему вы говорите, что оно имеет «особый смысл» именно в геометрии
Оно не то, чтобы имеет там особый смысл. Просто число Пи определено через геометрические примитивы: окружность и ее диаметр.
Эти примитивы, конечно, можно выразить и аналитически, оторвавшись от геометри в целом.
Но так или иначе, даже аналитическое определение числа Пи будет, в первую очередь, неразрывно связано с тригонометрическими функциями. А уже через них число Пи преобретает свое значение в математике.
То есть число Пи не было выдумано из головы или не было рассчитано из функций синуса/косинуса. Сначала просто «поделили» длину окружности на диаметр, а уже после этого обнаружилась связь этого числа с тригонометрическими функциями (опять же, объясняемая геометрически), которые распротсранились вообще по множеству уголков всех разделов математики.
Да, кстати, обитатели одномерного мира, вообще ничего не знающие об углах, тем не менее могут быть знакомы с «гармоническими» функциями, известными нам как синус и косинус. Для них это функция колебания двух тел, соединённых пружинкой. Как вы им будете объяснять, что их гармонические функции — на самом деле тригонометрические, и что для понимания их истинного смысла просто необходимо выйти в двумерное пространство и понять, что такое катет и гипотенуза?
А вы уверены, что гармонические колебания двух тел на пружинке вообще возможны физически в одномерном пространстве?
Т.к. иначе с тем же успехом можно в одномерном пространстве организовать колебания, которые объясняются линейными функциями :)
Т.к. иначе с тем же успехом можно в одномерном пространстве организовать колебания, которые объясняются линейными функциями :)
Если у них есть динамическая система, имеющая состояние устойчивого равновесия, зависимость энергии этой системы от виртуальных координат дважды дифференцируема, и выполняется закон сохранения энергии, то малое отклонение системы от состояния равновесия приведёт к гармоническим колебаниям (нужно ещё что-то сказать про вторые производные, но не помню, что именно). Условий много, но в «физическом», а не цифровом мире они вполне естественны. Ведь силы взаимодействия даже в нашем мире не всегда описываются законом Кулона, так что у них сила притяжения/отталкивания вполне может зависеть от расстояния.
Например, можно представить себе «пружинку» как цепочку атомов ненулевой длины, которые притягиваются, когда между ними есть зазор, но начинают отталкиваться, когда проникают друг в друга (сила отталкивания зависит от глубины проникновения). Надо посчитать наиболее правдоподобную модель, но линейный участок зависимости силы от длины пружинки там может найтись.
Например, можно представить себе «пружинку» как цепочку атомов ненулевой длины, которые притягиваются, когда между ними есть зазор, но начинают отталкиваться, когда проникают друг в друга (сила отталкивания зависит от глубины проникновения). Надо посчитать наиболее правдоподобную модель, но линейный участок зависимости силы от длины пружинки там может найтись.
Вы же понимаете, что утверждаете, по сути, то, что если у них есть система с гармоническими колебаниями, то у них есть система с гармоническими колебаниями?
Я к чему клоню.
Синус/косинус в гармонических колебаниях возникают тоже неслучайно.
В случае маятника, например, они там возникают вполне очевидным образом.
Но, например, в случае пружины тригонометрия возникает в момент, когда деформация сжатия/растяжения пружины преобразуется в деформацию кручения материала.
В случае одномерного пространства вращению взяться неоткуда, поэтому можно лишь рассматривать линейные тела. Однако, в этом случае гармонические колебания могут возникнуть только если мы вводим в созданную нами одномерную вселенную закон, по которому некий материал (или одномерные частицы в нем) допускает гармонические колебания.
Я к чему клоню.
Синус/косинус в гармонических колебаниях возникают тоже неслучайно.
В случае маятника, например, они там возникают вполне очевидным образом.
Но, например, в случае пружины тригонометрия возникает в момент, когда деформация сжатия/растяжения пружины преобразуется в деформацию кручения материала.
В случае одномерного пространства вращению взяться неоткуда, поэтому можно лишь рассматривать линейные тела. Однако, в этом случае гармонические колебания могут возникнуть только если мы вводим в созданную нами одномерную вселенную закон, по которому некий материал (или одномерные частицы в нем) допускает гармонические колебания.
Мы можем оперировать многомерными аналитическими пространствами и исследовать их свойства. Почему же одномерники не смогут найти такое свойство двумерного пространства, как Пи?
Потому что они найдут его раньше, как период гармонических колебаний. Уже потом, изучая фазовые пространства, они назовут один катет треугольника «положением», другой — «импульсом», гипотенузу — «энергией», а угол — «временем», и обнаружат геометрические свойства синуса. Может быть… Но могут обойтись без углов вообще — им это понятие не нужно. Разве что для многофакторного анализа… Но это будет потом.
Мы говорим о непротиворечащих одна другой вещах. Вы говорите, что к любому свойству pi можно притянуть за уши его геометрическое определение. Я же говорю, что может и можно, но совсем не обязательно от него отталкиваться. В частности, разрабатывая математику в сильно неевклидовом мире, в точно также упрёмся в константу pi, вне зависимоти от того, будет в нашем мира отношение длины окружности к диаметру постоянным или нет.
Что касается исходного вопроса из поста, то у меня к нему две претензии: Во-первых, я не согласен, что «pi как свойство пространство» корректно называть pi, во всяком случае в математике так никто не делает. Во-вторых, из постановки вопроса видно, что автор ожидает, что в нашем мире можно поменять пи, а всё остальное оставить. Это принципиально не так. Мы, конечно, можем задаться принципиальным вопросом описания всех возможных нормированных пространств, в которых все окружности имеют длину и эта длина в 6 раз больше радиуса, но этот вопрос — чисто математический, и до описания физических свойств таких пространств там ещё далеко.
Что касается исходного вопроса из поста, то у меня к нему две претензии: Во-первых, я не согласен, что «pi как свойство пространство» корректно называть pi, во всяком случае в математике так никто не делает. Во-вторых, из постановки вопроса видно, что автор ожидает, что в нашем мире можно поменять пи, а всё остальное оставить. Это принципиально не так. Мы, конечно, можем задаться принципиальным вопросом описания всех возможных нормированных пространств, в которых все окружности имеют длину и эта длина в 6 раз больше радиуса, но этот вопрос — чисто математический, и до описания физических свойств таких пространств там ещё далеко.
Однако, вопрос будет вполне корректный, если переформулировать, что будет, если соотношение длины окружности к диаметру равнялось бы трем.
Визуально такое пространство можно представить, как провисающий гамак — веревки гамака в данном случае будут являться геодезическими линиями.
А вот пространство, где l /d > Pi представить намного сложнее, во всяком случае мне не приходит в голову ни одна аналогия, где пространство было бы искажено однородно.
Визуально такое пространство можно представить, как провисающий гамак — веревки гамака в данном случае будут являться геодезическими линиями.
А вот пространство, где l /d > Pi представить намного сложнее, во всяком случае мне не приходит в голову ни одна аналогия, где пространство было бы искажено однородно.
Кстати, не факт, что скорость света и гравитационная постоянная не следуют из числа Pi и не столь же фундаментальны.
Как известно, если долго спорить, то в итоге приходишь к выяснению определений. Математическое пи, то есть отношение длины окружности к её диаметру в Евклидовом пространстве, равно константе 3,1415926… и появляется в разных математических формулах и рядах.
А вот реальное отношение длины окружности к диаметру в нашем пространстве не обязательно равно пи, и даже меняется в зависимости от локальной кривизны пространства, если судить по ответам в math.stackexchange.com/questions/53023/could-pi-have-a-different-value-in-a-different-universe и physics.stackexchange.com/questions/28065/pi-and-the-curvature-of-space.
А вот реальное отношение длины окружности к диаметру в нашем пространстве не обязательно равно пи, и даже меняется в зависимости от локальной кривизны пространства, если судить по ответам в math.stackexchange.com/questions/53023/could-pi-have-a-different-value-in-a-different-universe и physics.stackexchange.com/questions/28065/pi-and-the-curvature-of-space.
Вы не совсем правы, ответил выше, со второго абзаца.
Мой профессор высказался бы категоричнее: «вы совсем не правы».
Так как дело всего лишь в точности вычисления.
Мой профессор высказался бы категоричнее: «вы совсем не правы».
Так как дело всего лишь в точности вычисления.
Один из вариантов ответа — «с инженерных калькуляторов пропадет кнопка Pi» — вполне валиден, на мой взгляд.
После этого поста я понял одно — я ничего не смыслю в математике.
С запретом на косинус сразу вспоминается формула эйлера и ряд тригонометрических формул, которыми можно заменить косинус на совокупность других тригонометрических функций, да даже банальный cos(x) = sin(x — pi/2).
Про Pi=3 я бы ответил, что так как pi это не какая-то абстрактная величина, а вполне себе осязаемая и есть отношение длины окружности к её диаметру, то либо система исчисления в таком мире такая, что наши 3.14 просто равны их 3, то есть в основе у них не натуральные числа, а производные от пи.
Либо этот мир был бы с искажённым пространством, не изотропным, например если взять круг и сплюснуть его до овала, то можно получить радиус, равный ровно 3, то есть возможно одно измерение такого пространства было бы сужено и был бы эффект как у 4:3 фильма, растянутого на экран 16:9 — все толстые карлики.
Не жалейте, что не пошли к ним работать.
Про Pi=3 я бы ответил, что так как pi это не какая-то абстрактная величина, а вполне себе осязаемая и есть отношение длины окружности к её диаметру, то либо система исчисления в таком мире такая, что наши 3.14 просто равны их 3, то есть в основе у них не натуральные числа, а производные от пи.
Либо этот мир был бы с искажённым пространством, не изотропным, например если взять круг и сплюснуть его до овала, то можно получить радиус, равный ровно 3, то есть возможно одно измерение такого пространства было бы сужено и был бы эффект как у 4:3 фильма, растянутого на экран 16:9 — все толстые карлики.
Не жалейте, что не пошли к ним работать.
да даже банальный cos(x) = sin(x — pi/2)
Хм, тоже верно, но здесь есть один момент, как мне кажется.
Когда вы пишете, что первообразная sin(x) будет равна -sin(x-Pi/2), вы как бы пропускаете, что неявно используете cos(x). То есть это трюк, и я не уверен, можно ли его было использовать. Ведь если писать все действия последовательно, должно быть тогда так:
интеграл от sin(x) от 0 до Pi =-cos(x)|0..Pi=-sin(x-Pi/2)|0...Pi
То есть в выводе конечной формулы cos присутствует.
То же самое, если мы заменим cos(x) на 1/sec(x), неявно cos будет использоваться в промежуточных вычислениях.
Разве нет?
P.S. Мог ошибиться в знаках, ну вы поняли.
Хм, тоже верно, но здесь есть один момент, как мне кажется.
Когда вы пишете, что первообразная sin(x) будет равна -sin(x-Pi/2), вы как бы пропускаете, что неявно используете cos(x). То есть это трюк, и я не уверен, можно ли его было использовать. Ведь если писать все действия последовательно, должно быть тогда так:
интеграл от sin(x) от 0 до Pi =-cos(x)|0..Pi=-sin(x-Pi/2)|0...Pi
То есть в выводе конечной формулы cos присутствует.
То же самое, если мы заменим cos(x) на 1/sec(x), неявно cos будет использоваться в промежуточных вычислениях.
Разве нет?
P.S. Мог ошибиться в знаках, ну вы поняли.
1. Интеграл можно взять численно с любой нужной точностью. Как площадь фигуры под графиком:
integral = 0
dx = 1e-6
x = 0
while (x < PI) {
integral += sin(x) * dx;
x += dx
}
Самое грубое приближение, но работать будет. Я думаю, это был вопрос про умение искать простые решения. И ответ больше подходит для программиста, а не для сурового математика.
2. Про шары — ХЗ. Я бы рассуждать начал от математического определения шара (геометрическое место точек, расстояние которых до центра <= радиуса) и от определения «внутри». Взять какую-нибудь функцию расстояния, в которой шаром бы считалась какая-то хрень, вывернутая наизнанку. И тогда шар большего радиуса действительно будет содержаться в меньшем.
3. Про пи — тоже ХЗ. Главное её применение, насколько я понимаю, это связывать радиус окружности с её длиной. Получилось бы, что если Земля летает вокруг солнца на том же расстоянии, как сейчас, то по факту её линейная скорость бы снизилась (т.к. длина орбиты уменьшилась). Снизилась бы кинетическая энергия при той же массе. Из закона сохранения энергии следует, что пропорционально уменьшилась бы и энергия гравитационного взаимодействия. А там «свободной» можно считать только гравитационную постоянную. Что из этого следует — хз. Наверняка, рассуждения придут к какому-то фундаментальному противоречию, которое и будет доказывать нереальность исходного предположения. Это ли вообще интересовало интервьюера, не знаю.
В топик призывается интервьюер. Наверняка ведь читает. Может пояснит, что имелось в виду? Интересно же.
integral = 0
dx = 1e-6
x = 0
while (x < PI) {
integral += sin(x) * dx;
x += dx
}
Самое грубое приближение, но работать будет. Я думаю, это был вопрос про умение искать простые решения. И ответ больше подходит для программиста, а не для сурового математика.
2. Про шары — ХЗ. Я бы рассуждать начал от математического определения шара (геометрическое место точек, расстояние которых до центра <= радиуса) и от определения «внутри». Взять какую-нибудь функцию расстояния, в которой шаром бы считалась какая-то хрень, вывернутая наизнанку. И тогда шар большего радиуса действительно будет содержаться в меньшем.
3. Про пи — тоже ХЗ. Главное её применение, насколько я понимаю, это связывать радиус окружности с её длиной. Получилось бы, что если Земля летает вокруг солнца на том же расстоянии, как сейчас, то по факту её линейная скорость бы снизилась (т.к. длина орбиты уменьшилась). Снизилась бы кинетическая энергия при той же массе. Из закона сохранения энергии следует, что пропорционально уменьшилась бы и энергия гравитационного взаимодействия. А там «свободной» можно считать только гравитационную постоянную. Что из этого следует — хз. Наверняка, рассуждения придут к какому-то фундаментальному противоречию, которое и будет доказывать нереальность исходного предположения. Это ли вообще интересовало интервьюера, не знаю.
В топик призывается интервьюер. Наверняка ведь читает. Может пояснит, что имелось в виду? Интересно же.
этж классика =)
предположим a = b, тогда
a^2 = ab, домножим на π
πa^2 = πab (1)
кстати заметим что 3b^2 = 3a^2 = 3ab, вычтем из (1) то что мы заметили
πa^2 — 3ab = πab — 3b^2
добавим 3ab к обоимчастямуравнения
πa^2 = πab — 3b^2 + 3ab
и вычтем πab
πa^2 — πab =3ab — 3b^2
добавим ab
πa^2 — πab + ab = 3ab — 3b^2 + ab = 4ab — 3b^2
вычтем b^2
πa^2 — πab + ab — b^2 = 4ab — 3b^2 — b^2 = 4ab — 4b^2
немного алгебры
πa(a — b) + b(a — b) = 4b(a — b) => πa + b = 4b => πa = 3b
но ведь a=b, тогда
πa = 3b => πa = 3a => π = 3
предположим a = b, тогда
a^2 = ab, домножим на π
πa^2 = πab (1)
кстати заметим что 3b^2 = 3a^2 = 3ab, вычтем из (1) то что мы заметили
πa^2 — 3ab = πab — 3b^2
добавим 3ab к обоимчастямуравнения
πa^2 = πab — 3b^2 + 3ab
и вычтем πab
πa^2 — πab =3ab — 3b^2
добавим ab
πa^2 — πab + ab = 3ab — 3b^2 + ab = 4ab — 3b^2
вычтем b^2
πa^2 — πab + ab — b^2 = 4ab — 3b^2 — b^2 = 4ab — 4b^2
немного алгебры
πa(a — b) + b(a — b) = 4b(a — b) => πa + b = 4b => πa = 3b
но ведь a=b, тогда
πa = 3b => πa = 3a => π = 3
У меня одного сложилось впечатление, что A — высокомерный мудак?
ну и к предыдущему абсурду, добавлю еще капельку абсурдного рассуждения -)
Что если pi = 3. По определению — это отношение длины окружности к диаметру. Если попробовать представить что это, то мне например на ум приходит только конус; учитывая что я нахожусть в евклидовом пространстве (конечно это не так, но в масштабах комнаты в которой я нахожусь оно вполне эвклидово). Итак линии образующие поверхность конуса становятся радиусами, основание конуса становится той самой окружностью, длина которой равна 3*диаметр. А вот сам диаметр, который по определению является прямой, становиться не совсем прямой, а сломаной линией. И вообще конус — это 3д тело, а не 2д, так что заменить все круги конусами кажется не очень хорошей идеей, а тем более сделать какие то выводы. Тут мы вспопинаем о геометриях риммана или лобачевского, но ни одна нам не подходит, и подходящую мы врядли вспомним. Но все они характеризуются кривизной (вот ту я даже формул не помню, но продолжим =), а кривизна кривой в точке определеяется через производную, но наш «диаметр» в точке «центре окружности (вершине конуса)» имеет точку сингулярности и в ней очевидно производная не существует. Получается что все точки пространства станут сингулярностями и такое возможно в черной дыре. чтд. -)
Что если pi = 3. По определению — это отношение длины окружности к диаметру. Если попробовать представить что это, то мне например на ум приходит только конус; учитывая что я нахожусть в евклидовом пространстве (конечно это не так, но в масштабах комнаты в которой я нахожусь оно вполне эвклидово). Итак линии образующие поверхность конуса становятся радиусами, основание конуса становится той самой окружностью, длина которой равна 3*диаметр. А вот сам диаметр, который по определению является прямой, становиться не совсем прямой, а сломаной линией. И вообще конус — это 3д тело, а не 2д, так что заменить все круги конусами кажется не очень хорошей идеей, а тем более сделать какие то выводы. Тут мы вспопинаем о геометриях риммана или лобачевского, но ни одна нам не подходит, и подходящую мы врядли вспомним. Но все они характеризуются кривизной (вот ту я даже формул не помню, но продолжим =), а кривизна кривой в точке определеяется через производную, но наш «диаметр» в точке «центре окружности (вершине конуса)» имеет точку сингулярности и в ней очевидно производная не существует. Получается что все точки пространства станут сингулярностями и такое возможно в черной дыре. чтд. -)
Сотрудника компании X, случаем, не Олег зовут?
К сожалению, нередко собеседующие пытаются самоутверждаться за счёт собеседуемого.
Про интеграл. В институте рассказывали, как интегрировать, когда посчитать первообразную тяжело или невозможно. Интеграл — это площадь под кривой. Строите график. Потом вырезаете из бумаги площадь, соответствующую интегралу. Взвешиваете. Потом из той же бумаги вырезаете квадрат 1х1 (в единицах измерения, в которых строили график). Взвешиваете. Площадь квадрата 1 ед^2. Делите вес фигуры на вес этого квадрата. Получаете величину площади, а значит и сам интеграл.
Про Pi. Возможно, что имелось ввиду, что угловая скорость вращения — это o = 2 * Pi / T, где o — угловая скорость, а T — период обращения. Если предположить, что угловая скорость Земли и не меняется и для простоты она круговая, то из-за изменения Pi, будет меняться период обращения вокруг Солнца, т.е. длительность года. А намёк про Pi^2 мог быть связан с другой формулой: Fграв. = o^2 * R или Fграв. = 4 * Pi^2 * R / T^2, а Fграв. = G * M * m / R^2. Опять же можно порассуждать про длительность года, если R для Земли не меняется.
Про интеграл. В институте рассказывали, как интегрировать, когда посчитать первообразную тяжело или невозможно. Интеграл — это площадь под кривой. Строите график. Потом вырезаете из бумаги площадь, соответствующую интегралу. Взвешиваете. Потом из той же бумаги вырезаете квадрат 1х1 (в единицах измерения, в которых строили график). Взвешиваете. Площадь квадрата 1 ед^2. Делите вес фигуры на вес этого квадрата. Получаете величину площади, а значит и сам интеграл.
Про Pi. Возможно, что имелось ввиду, что угловая скорость вращения — это o = 2 * Pi / T, где o — угловая скорость, а T — период обращения. Если предположить, что угловая скорость Земли и не меняется и для простоты она круговая, то из-за изменения Pi, будет меняться период обращения вокруг Солнца, т.е. длительность года. А намёк про Pi^2 мог быть связан с другой формулой: Fграв. = o^2 * R или Fграв. = 4 * Pi^2 * R / T^2, а Fграв. = G * M * m / R^2. Опять же можно порассуждать про длительность года, если R для Земли не меняется.
Да, есть такие формулы (про Pi).
Я их не помнил, хоть они и простейшие. Признаю это.
Другой вопрос, почему угловая скорость не изменится? Может быть изменение Pi приведет к такому глубокому изменению всего и вся (поверить в это вполне можно), что угловая скорость тоже изменится сама по себе? И насколько она изменится?
То есть, я имею в виду, что сразу два аргумента в этой формуле могут измениться: и Pi и угловая скорость. Возможно ли это?
Вообще есть чисто формальный подход, основанный на анализе этой изолированной формулы, но не факт, что он правилен без какого-то более комплексного анализа ситуации с изменением Pi.
Насколько это критично для данной вакансии и именно ли это хотел проверить интервьюер — другой вопрос.
Я их не помнил, хоть они и простейшие. Признаю это.
Другой вопрос, почему угловая скорость не изменится? Может быть изменение Pi приведет к такому глубокому изменению всего и вся (поверить в это вполне можно), что угловая скорость тоже изменится сама по себе? И насколько она изменится?
То есть, я имею в виду, что сразу два аргумента в этой формуле могут измениться: и Pi и угловая скорость. Возможно ли это?
Вообще есть чисто формальный подход, основанный на анализе этой изолированной формулы, но не факт, что он правилен без какого-то более комплексного анализа ситуации с изменением Pi.
Насколько это критично для данной вакансии и именно ли это хотел проверить интервьюер — другой вопрос.
>К сожалению, нередко собеседующие пытаются самоутверждаться за счёт собеседуемого.
Согласен, на таких тратить время не хочу
Согласен, на таких тратить время не хочу
Задача интервьюера (на выбор):
1. Нанять людей из того-же ВУЗа, что и он сам, где им показали запретную магию, как посчитать этот интеграл правильным образом
2. Отсеять любых кандидатов с глубокими знаниями математики, чтобы чувствовать себя самым крутым математиком
3. Выплеснуть ненависть к математикам основанную на зависти, что они находят такие решения, которые он не понимает
4. Нанять докторов математических наук на должность аналитиков и готовых платить безумные деньги
1. Нанять людей из того-же ВУЗа, что и он сам, где им показали запретную магию, как посчитать этот интеграл правильным образом
2. Отсеять любых кандидатов с глубокими знаниями математики, чтобы чувствовать себя самым крутым математиком
3. Выплеснуть ненависть к математикам основанную на зависти, что они находят такие решения, которые он не понимает
4. Нанять докторов математических наук на должность аналитиков и готовых платить безумные деньги
5. Найти человека, который для решения задач не вспоминает занимательные факты из институтской программы, а умеет изобретать их на лету.
Найти человека, который сможет быстро и убедительно доказать клиенту что два равно трём, и что это не баг, а фича.
При этом клиент должен остаться доволен и поражён глубиной знаний своего собеседника.
При этом клиент должен остаться доволен и поражён глубиной знаний своего собеседника.
Вы не рассматривали данный вопрос как провокацию Вас в случае цейтнота и жестких начальных условий? Задача сама интересна по постановке, но не факт, что требовалось ее решение.
Если рассматривать постановку задачи в контексте проверки знаний математики, то тест вы возможно бы и сдали (хотя бы показав примерный ход размышлений)
Если рассматривать это, как оценку Ваших действий в сложных условиях, то тест вы провалили.
Допускаю, что начальной целью интервьюер ставил одну задачу, а после того как Вы не смогли предложить решение повысил свою самооценку тем, что «подвесил» кандидата, тем более с мат. образованием.
Если рассматривать постановку задачи в контексте проверки знаний математики, то тест вы возможно бы и сдали (хотя бы показав примерный ход размышлений)
Если рассматривать это, как оценку Ваших действий в сложных условиях, то тест вы провалили.
Допускаю, что начальной целью интервьюер ставил одну задачу, а после того как Вы не смогли предложить решение повысил свою самооценку тем, что «подвесил» кандидата, тем более с мат. образованием.
Каждый раз жду историю о том, как кандидат обыгрывает интервьюера (можно вымышленную).
Уважаемый автор,
как было бы здорово прочитать ваш пост в другом аспекте: смотрите, какие интересные задачи мне задали на собеседовании, давайте вместе их попробуем решить. А так… Вы выносите на всеобщее обозрение свою личную обиду на человека, который позволил себе проявить бестактность. Увы, это было всегда, люди не идеальны — но зачем умножать общее количество «мирового негатива» еще дальше? Вы получили ценный опыт, тот сотрудник наверняка тоже сделал какие-то выводы — все счастливы)
Касательно задачи про Pi == 3, есть разные статьи на эту тему.
как было бы здорово прочитать ваш пост в другом аспекте: смотрите, какие интересные задачи мне задали на собеседовании, давайте вместе их попробуем решить. А так… Вы выносите на всеобщее обозрение свою личную обиду на человека, который позволил себе проявить бестактность. Увы, это было всегда, люди не идеальны — но зачем умножать общее количество «мирового негатива» еще дальше? Вы получили ценный опыт, тот сотрудник наверняка тоже сделал какие-то выводы — все счастливы)
Касательно задачи про Pi == 3, есть разные статьи на эту тему.
Автор работу ищет. Какого черта он должен терять время на таких умников?
Ладно г-ну А нехрен делать на работе и он развлекается поглаживая свое ЧСВ. Но почему за счет других людей?
Пусть идет в любую флудильню и сверкает там всеми своими гранями.
Автор! К черту предрассудки с «джентельменским» поведением. Огласите контору и спасите от мудака многих других. У вас может и не все так драматично, но есть же люди которые ищут работу и найти ее надо в сжатые сроки. То что он удалил обсуждение в фейсбуке значит только одно — ему по шапке надают если про такие его развлечения узнают.
Ладно г-ну А нехрен делать на работе и он развлекается поглаживая свое ЧСВ. Но почему за счет других людей?
Пусть идет в любую флудильню и сверкает там всеми своими гранями.
Автор! К черту предрассудки с «джентельменским» поведением. Огласите контору и спасите от мудака многих других. У вас может и не все так драматично, но есть же люди которые ищут работу и найти ее надо в сжатые сроки. То что он удалил обсуждение в фейсбуке значит только одно — ему по шапке надают если про такие его развлечения узнают.
То что А поступил не вполне корректно — факт.
Смысл моего комментария в том, что хабр — не место для обсуждения плохого поведения людей, для этого есть zadolba.li. и прочие подобные. Жаловаться на людей и обстоятельства — не самое лучшее, чему можно посветить время, свое и читателей. Здесь очень много одаренных людей, стремящихся использовать свои интеллектуальные и творческие способности для создания удивительных вещей, смелых проектов и открытий — так не будем же опускаться до уровня А, публично комментируя чье-то поведение.
Сэкономить время тем, кто ищет работу — мотив хороший, однако:
1. Для меня бы это не стало сигналом «туда не ходи». Может это в целом вполне хорошая компания, я бы не стал делать выводы по одному человеку.
2. Опять же, хабр это не «черный список работодателей».
Смысл моего комментария в том, что хабр — не место для обсуждения плохого поведения людей, для этого есть zadolba.li. и прочие подобные. Жаловаться на людей и обстоятельства — не самое лучшее, чему можно посветить время, свое и читателей. Здесь очень много одаренных людей, стремящихся использовать свои интеллектуальные и творческие способности для создания удивительных вещей, смелых проектов и открытий — так не будем же опускаться до уровня А, публично комментируя чье-то поведение.
Сэкономить время тем, кто ищет работу — мотив хороший, однако:
1. Для меня бы это не стало сигналом «туда не ходи». Может это в целом вполне хорошая компания, я бы не стал делать выводы по одному человеку.
2. Опять же, хабр это не «черный список работодателей».
По п.п. 1 и 2:
Где вы у меня увидели «черный список работодателей»?
Покажите точную цитату, пожалуйста.
Я нигде не говорил, что это плохая компания.
Более того, я так не думаю ни до, ни после собеседования.
Я не исключаю для себя возможности в будущем рассмотреть какие-то другие вакансии этой компании.
Вас никто не просит комментировать чье-то поведение, если вам это неприятно.
Комментируйте содержание собеседования (задачки), если вам интересно.
У меня больше половины топика посвящены именно задачкам и ходу их решения, а не описанию чьего-либо поведения.
Выше было показано, насколько глубокий анализ может быть сделан.
И несколько людей его сделали, за что им большое спасибо!
Если вам есть что сказать — скажите.
За ссылку выше — спасибо.
Где вы у меня увидели «черный список работодателей»?
Покажите точную цитату, пожалуйста.
Я нигде не говорил, что это плохая компания.
Более того, я так не думаю ни до, ни после собеседования.
Я не исключаю для себя возможности в будущем рассмотреть какие-то другие вакансии этой компании.
так не будем же опускаться до уровня А, публично комментируя чье-то поведение
Вас никто не просит комментировать чье-то поведение, если вам это неприятно.
Комментируйте содержание собеседования (задачки), если вам интересно.
У меня больше половины топика посвящены именно задачкам и ходу их решения, а не описанию чьего-либо поведения.
Выше было показано, насколько глубокий анализ может быть сделан.
И несколько людей его сделали, за что им большое спасибо!
Если вам есть что сказать — скажите.
За ссылку выше — спасибо.
зачем такой откровенный стеб еще и решать?
Ну что я бы на вашем месте радовался
1. Вы избежали работы в коллективе с непорядочными руководителями что есть благо :) Помимо этого на лицо непонимание и прочие антиплюшки
2. Благодаря вашему пусть не совсем приятному опыту на хабре получили удовольствие много достаточно умных людей. Что есть несомненное благо
1. Вы избежали работы в коллективе с непорядочными руководителями что есть благо :) Помимо этого на лицо непонимание и прочие антиплюшки
2. Благодаря вашему пусть не совсем приятному опыту на хабре получили удовольствие много достаточно умных людей. Что есть несомненное благо
У меня было на нескольких собеседованиях совсем аналогичные ситуации. Я лично такому не удивляюсь, хотя обидно.
автор, какие 367 теорем пифагора?? это не собеседование а хрень собачья. уже на второй теореме я спрошу целесообразность задаваемого «а что если» и необходимость использования её в работе, а на третьей просто пошлю на фиг. (а на четвертой могу и в морду дать:) соискатель же не дурак, и видит что над ним просто издеваются
Я бы на подсчёт интеграла без косинуса ответил так. Нарисовал полукруг. Сказал, что проекция малой дуги длиной dl на диаметр равна dl*sin(a). Поэтому длина диаметра — интеграл от синуса, как раз от 0 до pi. А эта длина равна 2.
Про pi=3 — даже не знаю, что они хотели бы услышать. В голову приходит, что тогда было бы возможно sin(x)>x при некоторых x>0 (например, x=1/4, sin(x)=(sqrt(6)-sqrt(2))/4=0.2588...). Но в целом — ничего интересного бы не произошло, не считая того, что такого мира существовать не может. Были бы проблемы с правильными многоугольниками, у которых 6 и более вершин — но в какой-нибудь сферической геометрии они и так есть…
Про pi=3 — даже не знаю, что они хотели бы услышать. В голову приходит, что тогда было бы возможно sin(x)>x при некоторых x>0 (например, x=1/4, sin(x)=(sqrt(6)-sqrt(2))/4=0.2588...). Но в целом — ничего интересного бы не произошло, не считая того, что такого мира существовать не может. Были бы проблемы с правильными многоугольниками, у которых 6 и более вершин — но в какой-нибудь сферической геометрии они и так есть…
Здравствуйте!
Простите, не совсем понял ваше решение про интеграл без косинуса.
Можете его расписать чуть подробнее (т.е. шаг от выражения dl*sin(a) до уже интегральной формулы)?
Идею я вашу понял, но у меня получается иначе:
Чтобы вычислить длину диаметра d, параметризуем его через угол a:
x(a)=cos(a), y(a)=0; a принимает значения от 0 до Pi,
тогда d=интеграл от 0 до Pi sqrt(((cos'(a))^2)) da=интеграл от 0 до Pi sqrt(((sin(a))^2) da = интеграл от 0 до Pi sin(a) da
использовал формулу для вычисления длины параметризованной кривой отсюда
Отсюда 2=интеграл от 0 до Pi sin(a) da
Но! Здесь проблема в том, что cos фигурирует в промежуточных вычислениях.
Простите, не совсем понял ваше решение про интеграл без косинуса.
Можете его расписать чуть подробнее (т.е. шаг от выражения dl*sin(a) до уже интегральной формулы)?
Идею я вашу понял, но у меня получается иначе:
Чтобы вычислить длину диаметра d, параметризуем его через угол a:
x(a)=cos(a), y(a)=0; a принимает значения от 0 до Pi,
тогда d=интеграл от 0 до Pi sqrt(((cos'(a))^2)) da=интеграл от 0 до Pi sqrt(((sin(a))^2) da = интеграл от 0 до Pi sin(a) da
использовал формулу для вычисления длины параметризованной кривой отсюда
Отсюда 2=интеграл от 0 до Pi sin(a) da
Но! Здесь проблема в том, что cos фигурирует в промежуточных вычислениях.
Действуем по определению интеграла как предела интегральных сумм.
У нас есть полуокружность, параметризованная углом от 0 до pi. Разбиваем её на N дуг равной длины.
Пусть одна из дуг идёт от угла a до b. Берём хорду, соединяющую её конечные точки. Перпендикуляр к ней пересекает диаметр под углом (a+b)/2, поэтому проекция хорды на диаметр равна L*sin((a+b)/2), где L — длина хорды. Сумма проекций равна 2, откуда следует, что. интегральная сумма равна 2*(pi/(N*L)). Но N*L стремится к pi (длина дуги — предел длин ломаных, приближающих её), т.е. предел интегральных сумм равен 2.
Сплошная геометрия и никаких косинусов. Судя по следующему вопросу, могло и пройти.
У нас есть полуокружность, параметризованная углом от 0 до pi. Разбиваем её на N дуг равной длины.
Пусть одна из дуг идёт от угла a до b. Берём хорду, соединяющую её конечные точки. Перпендикуляр к ней пересекает диаметр под углом (a+b)/2, поэтому проекция хорды на диаметр равна L*sin((a+b)/2), где L — длина хорды. Сумма проекций равна 2, откуда следует, что. интегральная сумма равна 2*(pi/(N*L)). Но N*L стремится к pi (длина дуги — предел длин ломаных, приближающих её), т.е. предел интегральных сумм равен 2.
Сплошная геометрия и никаких косинусов. Судя по следующему вопросу, могло и пройти.
Вы забыли, надо ещё и без бумаги и ручки.
Нарисовать можно пальцем в воздухе, это не проблема.
Мое мнение:
Бумага нужна не только для промежуточных вычислений (хотя это самое важное, безусловно).
Бумага с ручкой также позволяет вспомнить то, что вы давно помнили, но забыли.
Когда вы нарисуете что-то (даже график того же синуса, круг, на котором изображен угол, радиус, Pi, или даже само изображение SIN), может, извлечение информации, относящейся к этой области данных из долговременной памяти происходит быстрее и легче, чем если вы только подумаете об этом.
Так как, возможно, какие-то ассоциации начнут проявлять свою активность, если на вход подан зрительный образ.
P.S. не претендую на научность.
Бумага нужна не только для промежуточных вычислений (хотя это самое важное, безусловно).
Бумага с ручкой также позволяет вспомнить то, что вы давно помнили, но забыли.
Когда вы нарисуете что-то (даже график того же синуса, круг, на котором изображен угол, радиус, Pi, или даже само изображение SIN), может, извлечение информации, относящейся к этой области данных из долговременной памяти происходит быстрее и легче, чем если вы только подумаете об этом.
Так как, возможно, какие-то ассоциации начнут проявлять свою активность, если на вход подан зрительный образ.
P.S. не претендую на научность.
По поводу интеграла — имхо «подсчитать без косинуса» звучит странно, но я бы разбил на две части по Pi/2 и сделал замену x = arcsin(tau). Тогда интеграл превращается в алгебраический.
Может просто сотрудник компании, который проводил собеседование имел в виду другого кандидата? Которого он действительно ввел в ступор на целых 10 минут. И задает одни и те же вопросы каждому кандидату и тупо смотрит на их реакцию )))
А мне кажется, сотрудник А хотел проверить, помнит ли кандидат значения функции sin(x) при определенных значениях. Если мы вспомним из школьного курса математики, что sin(0)=0, sin(pi/2)=1 и sin(pi)=0, и представим себе синусоиду (которая будет частью окружности, которая пересекается с абсциссой в точке 0 и 2), решение было бы мгновенным, не так ли? Либо кандидату ответ нужно было помнить наизусть?
Я не знаю, что за организация, куда устраивался кандидат, и что за должность его ждала, возможно, такие вещи и вправду нужны для этой должности. Но выкладывать что-то в фейсбуке и т.д. об этом мне кажется недопустимым, или интервьюер сам не наигрался еще? Он что, хотел разобраться, почему кандидаты не знают таких вещей? Или что за цель он преследовал? Неужели столько много времени у человека, чтобы сидеть и строчить в фейсбук про это? А то, что само по себе интервью это некий стресс, из-за которого из головы может вылететь все что угодно он не учел? Или этот вопрос настолько простой, что на него должен был ответить любой, разбуди его среди ночи?
Я не знаю, что за организация, куда устраивался кандидат, и что за должность его ждала, возможно, такие вещи и вправду нужны для этой должности. Но выкладывать что-то в фейсбуке и т.д. об этом мне кажется недопустимым, или интервьюер сам не наигрался еще? Он что, хотел разобраться, почему кандидаты не знают таких вещей? Или что за цель он преследовал? Неужели столько много времени у человека, чтобы сидеть и строчить в фейсбук про это? А то, что само по себе интервью это некий стресс, из-за которого из головы может вылететь все что угодно он не учел? Или этот вопрос настолько простой, что на него должен был ответить любой, разбуди его среди ночи?
Синусоида — совсем не окружность.
Намотать её на цилиндр с подходящим сечением — станет окружностью.
Не понял, приведите, пожалуйста, пример такого цилиндра. Синусоида — даже не эллипс, чтобы получить из нее окружность надо наложить ее на весьма странную и искревленную поверхность. После такого преобразования уже нельзя будет просто взять и подсчитать площадь. В любом случае, найти площать под синусоидой без использования тригонометрических функций, через площать каких-то известных фигур — так просто не выйдет.
Да, скорее всего, не получится. Можно добиться того, чтобы она вся лежала на одной сфере (но уравнение сечения цилиндра будет очень непростым). Чтобы кривая «свёрнутой» синусоиды осталась именно окружностью, она должна быть плоским сечением, значит, прямое сечение цилиндра должно быть эллипсом, а длина эллиптической дуги через синус не выражается. Вряд ли что-нибудь получится.
Интересно, как в 17-м веке считали площадь под дугой циклоиды (и длину её дуги). Интегралов тогда ещё не было.
Интересно, как в 17-м веке считали площадь под дугой циклоиды (и длину её дуги). Интегралов тогда ещё не было.
Конечно, я имел ввиду не окружность в ее полном понимании, этот термин привел для наглядности, наверное, нужно было написать по-другому (дуги например).
Все равно, непонятно. Как из фактов, что синусоида — это дуга, проходящая через точки (0,0), (0.5, Pi) и (1, 0), найти площадь под ней, при чем мгновенно (как написанно у вас)?
Честно говоря, математически я вам объяснить не смогу, так как просто не вспомню сейчас (не математик, и не занимался такими вещами как расчеты интегралов и т.д. больше 10 лет). Кстати точки немного другие (0,0) (0,5pi, 1) (pi,0).
Скорее всего, дело связано с пределами, которые обозначены в задаче и самой функцией sin(x). Эта задача становится очень простой, когда вы знаете на нее ответ. Нас учили в школе представлять графики функций, через какие точки они проходят, чтобы запомнить некоторые значения, которые часто используются в задачах. Замените значения 0,5pi и pi на 1 и 2 на оси абсцисс образно, и вы увидите ответ.
Посчитайте тот же пример с верхним пределом 0,5pi с использованием первообразной (cos(x)) вы увидите, что ответ будет 1. Очень просто запомнить, не так ли?
Конечно, это работает только с такими целыми пределами (pi) и невозможно быстро посчитать, если бы верхним пределом было бы какое-то число, не кратное pi. Вот что имелось ввиду.
Скорее всего, дело связано с пределами, которые обозначены в задаче и самой функцией sin(x). Эта задача становится очень простой, когда вы знаете на нее ответ. Нас учили в школе представлять графики функций, через какие точки они проходят, чтобы запомнить некоторые значения, которые часто используются в задачах. Замените значения 0,5pi и pi на 1 и 2 на оси абсцисс образно, и вы увидите ответ.
Посчитайте тот же пример с верхним пределом 0,5pi с использованием первообразной (cos(x)) вы увидите, что ответ будет 1. Очень просто запомнить, не так ли?
Конечно, это работает только с такими целыми пределами (pi) и невозможно быстро посчитать, если бы верхним пределом было бы какое-то число, не кратное pi. Вот что имелось ввиду.
1) ну если sin^2 ( x ) + cos^2 ( x ) = 1
а косинус использовать нельзя — то исходя из формулы можно и без косинуса? корень из единицы минус квадрат синуса? может это имелось в виду?
2) возможно (хотя вряд ли), целью собеседования являлось выяснение как поведет себя кандидат, перед которым ставится непонятная/некорректная задача — начнет ли нервничать? начнет ли фантазировать? начнет ли задавать уточняющие вопросы? в общем — как себя поведет?
а косинус использовать нельзя — то исходя из формулы можно и без косинуса? корень из единицы минус квадрат синуса? может это имелось в виду?
2) возможно (хотя вряд ли), целью собеседования являлось выяснение как поведет себя кандидат, перед которым ставится непонятная/некорректная задача — начнет ли нервничать? начнет ли фантазировать? начнет ли задавать уточняющие вопросы? в общем — как себя поведет?
что было бы в мире, если бы Pi было бы равным 3.
You Aren't Gonna Need It.
You Aren't Gonna Need It.
Если отбросить в сторону собственно рассуждения по сути вопросов — мне кажется странным способ проведения собеседования с математиком с запретом использовать бумагу и ручку.
Вообще любой кандидат это кот в мешке, по идее собеседование должно оценить его уровень как специалиста, и как-то «вскрыть» его с тем чтобы понять каково будет с ним работать как с человеком.
Судя по описанию, у интервьювера скорее была цель «опустить» — остаётся только гадать зачем. Часто это используется для того чтобы снизить зарплатные требования.
Вообще любой кандидат это кот в мешке, по идее собеседование должно оценить его уровень как специалиста, и как-то «вскрыть» его с тем чтобы понять каково будет с ним работать как с человеком.
Судя по описанию, у интервьювера скорее была цель «опустить» — остаётся только гадать зачем. Часто это используется для того чтобы снизить зарплатные требования.
По содержанию фейсбуковской заметки А и его дальнейшим действиям (стирание записи с разоблачающими комментариями и последующее стыдливое помалкивание) можно сделать однозначный вывод что А:
1)Высокомерен.
2)Труслив.
3)Некомпетентен.
4)Нетактичен.
Оборони Б-г от таких начальников.
1)Высокомерен.
2)Труслив.
3)Некомпетентен.
4)Нетактичен.
Оборони Б-г от таких начальников.
это называется профнепригдность
Я извиняюсь, но мне кажется, что вы пытаетесь составить своё мнение о человеке, которого никогда в жизни не видели, опираясь лишь на цитату одной единственной записи в социальной сети. Может быть у него какая-то серьёзная проблема в семье, или собеседование совпало с обострением депрессии, или может быть у него полгода секса не было, или автор статьи умолчал о своём хамском поведении (Я только предполагаю, перебираю варианты и не пытаюсь никого оправдать). Вся ситуация, описанная в статье, по большей части подана со стороны соискателя. А мнение противоположной стороны практически не видно.
Это напоминает мне фильм Акиры Куросавы «Расёмон». В этом фильме режиссёр показал несколько точек зрения на одно и то же событие от разных свидетелей. Оказалось, что восприятие ситуации у каждого участника была своё собственное. Очень рекомендую к просмотру.
Это напоминает мне фильм Акиры Куросавы «Расёмон». В этом фильме режиссёр показал несколько точек зрения на одно и то же событие от разных свидетелей. Оказалось, что восприятие ситуации у каждого участника была своё собственное. Очень рекомендую к просмотру.
Если построить интеграл от Sin(X), то станет очевидно, что это точно такая же синусоида, как и исходная, только смещённая по X на 3Pi/2. Что, кстати, доказывается через формулы приведения:
-Cos(x)=Sin(3Pi/2+X)
Далее просто подставляем 0 и Pi… Но вот как, не зная формул приведения и не имея бумажки (или настолько развитого воображения, чтобы графики в уме строить) прийти к такому выводу?
Тут сразу вспоминаются школьные олимпиады по информатике за 11 класс, которые в своё время напрочь убили у меня желание поступать на ФПМ. Потому что шёл-то я на олимпиаду по программированию, а получил задачки по чистой математике, где требовалось сперва вывести нетривиальную формулу, потом доказать методом мат.индукции, что она верна, ну и когда такая формула есть, то задача решается двумя строчками кода и тем самым не представляет ни малейшего интереса.
-Cos(x)=Sin(3Pi/2+X)
Далее просто подставляем 0 и Pi… Но вот как, не зная формул приведения и не имея бумажки (или настолько развитого воображения, чтобы графики в уме строить) прийти к такому выводу?
Тут сразу вспоминаются школьные олимпиады по информатике за 11 класс, которые в своё время напрочь убили у меня желание поступать на ФПМ. Потому что шёл-то я на олимпиаду по программированию, а получил задачки по чистой математике, где требовалось сперва вывести нетривиальную формулу, потом доказать методом мат.индукции, что она верна, ну и когда такая формула есть, то задача решается двумя строчками кода и тем самым не представляет ни малейшего интереса.
В этой статье для меня осталось много непонятного (например я не могу представить мир где пи=3 в принципе, хотя пытался делать это и раньше) но что действительно непонятно так это зачем был введен действующий персонаж B, он же представитель HR? Наплодили сущностей, я всю статью ждал когда же этот хр наконец выйдет на сцену и в качестве какого персонажа, негативного или позитивного :)
Знакомая ситуация: иногда на собеседованиях предлагают решить проблему при условии неполной информации, для этого требуется сообразительность, смекалка, иногда знания. Но в любом случае это не должно быть в тягость, как и любое другое собеседование.
Мой личный опыт-если человек, проводящий собеседование начинает мудрить, ну там ставить задачи из разряда давайте отменим косинус и число ПИ, не может четко сформулировать какую задачу он ставит, какие данные известны а какие нет-я просто встаю и ухожу, ибо собеседование, начавшееся плохо не может хорошо закончится.Также, если кто-то просит написать программу более 10 строк, взять интеграл, решить дифур или по другому продемонстрировать свои навыки и умения-я встаю и ухожу. Для демонстрации навыков и умений будет 3 месяца испытательного срока, и если им что-то не понравится (или мне не понравится) мы расстанемся.
Лично я рассматриваю собеседования как общение людей, которые заинтересованы друг в друге а не как попытки друг друга наколоть. Если кто-то во мне не заинтерисован или мне не нравится отношение, то зачем мне мучатся?
Мой личный опыт-если человек, проводящий собеседование начинает мудрить, ну там ставить задачи из разряда давайте отменим косинус и число ПИ, не может четко сформулировать какую задачу он ставит, какие данные известны а какие нет-я просто встаю и ухожу, ибо собеседование, начавшееся плохо не может хорошо закончится.Также, если кто-то просит написать программу более 10 строк, взять интеграл, решить дифур или по другому продемонстрировать свои навыки и умения-я встаю и ухожу. Для демонстрации навыков и умений будет 3 месяца испытательного срока, и если им что-то не понравится (или мне не понравится) мы расстанемся.
Лично я рассматриваю собеседования как общение людей, которые заинтересованы друг в друге а не как попытки друг друга наколоть. Если кто-то во мне не заинтерисован или мне не нравится отношение, то зачем мне мучатся?
Ещё вариант ответа на «что если pi=3»:
Можно начать дебагинг мира и математики. Выбрать факты, из которых сейчас следует, что pi>3, и начать их проверять. Посчитать углы правильного треугольника. Сторону вписанного правильного 6-угольника. Площадь вписанного правильного 12-угольника. Если получим 60 гр, 1, 3 (как в нашем мире) — то что-то не так с утверждением pi=3. Если они другие — изменились формулы расчётов, надо искать, в каком месте.
Ещё можно посчитать сумму 4*(1-1/3+1/5-....-1/15). Сейчас она больше 3. Если pi=3 — значит, либо сумма ряда перестала равняться pi (и изменились свойства арктангенса), либо частичная сумма стала меньше 3 — значит, изменилась арифметика, можно искать противоречия в аксиоматике Пеано (и в случае успеха требовать Нобелевскую премию по математике :) )
Можно начать дебагинг мира и математики. Выбрать факты, из которых сейчас следует, что pi>3, и начать их проверять. Посчитать углы правильного треугольника. Сторону вписанного правильного 6-угольника. Площадь вписанного правильного 12-угольника. Если получим 60 гр, 1, 3 (как в нашем мире) — то что-то не так с утверждением pi=3. Если они другие — изменились формулы расчётов, надо искать, в каком месте.
Ещё можно посчитать сумму 4*(1-1/3+1/5-....-1/15). Сейчас она больше 3. Если pi=3 — значит, либо сумма ряда перестала равняться pi (и изменились свойства арктангенса), либо частичная сумма стала меньше 3 — значит, изменилась арифметика, можно искать противоречия в аксиоматике Пеано (и в случае успеха требовать Нобелевскую премию по математике :) )
Пословицы в тему отсюда:
Один дурак может больше спросить, чем сто умных — ответить.
Один дурак скажет — сто мудрецов не разберут.
От старых дураков и молодым житья нет.
// В последней пословице под возрастом можно понимать стаж работы в компании Х.
В геометрии на сфере отношение диаметра окружности к её длине не равно Pi, кстати.
А шар большего диаметра внутри малого — там метрику с помощью инверсии надо делать, так? Хотя что значит «внутри» тогда, надо еще разобраться.
Один дурак может больше спросить, чем сто умных — ответить.
Один дурак скажет — сто мудрецов не разберут.
От старых дураков и молодым житья нет.
// В последней пословице под возрастом можно понимать стаж работы в компании Х.
В геометрии на сфере отношение диаметра окружности к её длине не равно Pi, кстати.
А шар большего диаметра внутри малого — там метрику с помощью инверсии надо делать, так? Хотя что значит «внутри» тогда, надо еще разобраться.
У вас ошибка в статье. Крупная известная компания, в которой открыта вакансия аналитика не X, а Y.
как вариант, аналитика-аналитике рознь. в фундаментальной науке принято все подвергать сомнению и докапываться до основ. если таким методом пытаться разораться в бизнес-процессах, скорее всего окажется, что в роли фундаментальных констант здесь выступят человеческая глупость и алчность. но какой в этом прок? часто работа аналитика сводится к тому, чтобы в проблеме клиента определить выгодный аспект, предложить свой вариант и убедить в том, что он единственно правильный. возможно, А искал себе на роль аналитика хитрого пройдоху, способного «продавать» решение, нежели неуверенного в себе математика.
// нельзя использовать cos. а почему, собственно? может на вашем калькуляторе нужная кнопка опять сломалась? sin же работает — давайте посчитаем — не проблема, всего в стопятсот раз дороже выйдет. кстати, вычислительные комплексы, которые я разрабатываю на текущем месте работы у ваших прямых конкурентов, обеспечивают беспрецедентную отказоустойчивость при работе с любыми тригонометрическими функциями…
// нельзя использовать cos. а почему, собственно? может на вашем калькуляторе нужная кнопка опять сломалась? sin же работает — давайте посчитаем — не проблема, всего в стопятсот раз дороже выйдет. кстати, вычислительные комплексы, которые я разрабатываю на текущем месте работы у ваших прямых конкурентов, обеспечивают беспрецедентную отказоустойчивость при работе с любыми тригонометрическими функциями…
Кстати, небольшим жонглированием с заменой переменных можно обойтись без косинуса:
Хорошее решение. Вроде ошибка в знаке в нижней строчке, но это несущественно (придирка).
Только не все вспомнят (или успеют вывести) производную арксинуса на собеседовании, особенно, без бумажки.
Только не все вспомнят (или успеют вывести) производную арксинуса на собеседовании, особенно, без бумажки.
Если уж писать решение, то полностью. Используем подстановку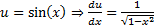 
и получаем
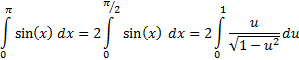
Теперь используем подстановку
и получим
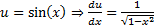и получаем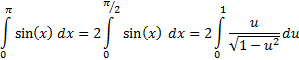Теперь используем подстановку
и получим
А собеседующим был… Альберт Эйнштейн
Раз уж тут собралось такое количество математиков и им сочувствующих, вот вам задачка, которой я любил троллить своих одноклассников и одногруппников во время учёбы. =)
— Назовите число, в два раза большее минус единицы
— Назовите число, в два раза большее минус единицы
— Назовите число, в два раза большее минус единицы
Прикольная задачка!
Решение, на мой взгляд, выглядит следующим образом:
пусть А — искомое число, тогда должно одновременно выполняться два условия:
1) А>-1 ( т.к. А больше -1)
2) А=(-1)*2 (т.к. А в точности равно удвоенному значению -1)
Из этих двух условий вытекает противоречие: -2>-1
Отсюда я бы лично сделал вывод, что отношения вида «X в N раз больше Y» для случая, если любое из чисел X или Y отрицательно, а N положительно, некорректны, во всяком случае, если мы работаем в обычной арифметике.
Проблема здесь в том, что ваше предложение содержит сразу два различных условия, которые в случае отрицательных чисел являются взаимно противоречивыми.
С другой стороны, для положительных чисел эти два условия они являются избыточными (можно оставить только условие A=2*B).
Чтобы не было противоречия, я бы порекомендовал говорить просто «назовите число, которое равно удвоенному значению -1»
Ответ -1/2 должен подойти. Больше? Да. Отношение — двойка? Да. А что не 2*х, это проблемы спрашивающего.
Я поздно прочитал этот топик, и ужасно удручает то, что люди плюсуют несущего чушь eterevsky и минусуют его оппонентов…
По поводу pi=3…
Вспоминается куръёз как в одном из американских штатов пи законодательно приравняли четырём. И вроде как мироздание целёхонько до сих пор… )))
На самом деле просто меняется система счисления (пусть даже и применительно только к этой константе).
Вспоминается куръёз как в одном из американских штатов пи законодательно приравняли четырём. И вроде как мироздание целёхонько до сих пор… )))
На самом деле просто меняется система счисления (пусть даже и применительно только к этой константе).
Зарегистрируйтесь на Хабре, чтобы оставить комментарий
История одного собеседования, или как в компании X кандидата «вешали»