Постановка задачи
Это вторая, итоговая статья. Напоминаю цель: есть двигатель постоянного тока. Задача — разработать, собрать и протестировать устройство, позволяющиее реализовать контур управления с заданием тока применительно к этому двигателю. Желаемое время переходного процесса на застопоренном двигателе (без противо-ЭДС) — не более 10мс.
Текст разбит на две статьи:
- 1. Измерение сопротивления и индуктивности двигателя
- 2. Разработка управляющего контура
Напоминаю, как выглядит макет управляющего железа:

Желаемый результат
Вся система как чёрный ящик
Итак, вся затея состоит в том, что я хочу напрямую задавать силу тока, протекающего через мой двигатель. Если объединить контроллер и двигатель воедино, то я бы хотел получить примерно следующее:

Здесь J(t) — это задание по току, I(t) — это ток, протекающий через двигатель. Я бы хотел, чтобы входной и выходной сигналы были бы связаны по закону τ I'(t) + I(t) = J(t). Этот закон выбран произвольно, просто мне нравится такое дифференциальное уравнение. Умными словами оно называется апериодическим звеном первого порядка. Контроллеры, подчиняющиеся такому закону даже имееют свой собственный символ на некоторых схемах:

Вот реакция подобного звена на единичное ступенчатое воздействие:
Это красивая экспоненциальная сходимость без разнообразных колебаний, поэтому такая форма и была выбрана. Постоянная тау в формуле τ I'(t) + I(t) = J(t) называется постоянной времени, это то время, за которое процесс достигнет 63% своего конечного значения при реакции на единичный скачок. Если определить время переходного процесса как время достижения 98% конечного значения, то это примерно 5 тау. В постановке задачи у нас время переходного процесса не должно превосходить 10мс, поэтому возьмём τ = 0,002.
Приоткроем чёрный ящик
Если же чёрный ящик приоткрыть, то выглядеть он будет как-то так:

На вход чёрного ящика подаём сигнал J(t), на выход получаем протекающий ток I(t). Внутри чёрного ящика два подъящика: двигатель со своим диффуром, связывающим напряжение на клеммах U(t) с протекающим через него током I(t), и непосредственно регулятор, который должен подавать напряжение U(t) в зависимости от задания тока J(t) и реально протекающего тока I(t).
Давайте скажем, что регулятор берёт на вход ошибку E(t) — это разница между желаемой силой тока и реальной, и на выход даёт напряжение U(t). Наша задача найти диффур, который связывает E(t) и U(t), тогда будет понятно, как программировать ардуину контроллера.
Итак, мы хотим, чтобы задание тока и реальный ток были бы связаны по выбранному нами закону:
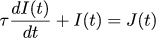
Применим к нему преобразование Лапласа (с нулевыми начальными значениями):
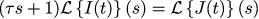
И составим следующую пропорцию:

На всякий случай, в теории управления эта пропорция называется передаточной функцией.
Определим ошибку E(t) как разницу между желаемой и реальной силой тока:
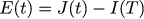
Для настройки контура тока зафиксируем вал двигателя, таким образом угловая скорость уходит из диффура двигателя:
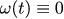
В предыдущей статье мы вывели связь между напряжением на клеммах мотора и силой протекающего тока (при зафиксированном роторе):
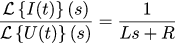
Давайте поделим эту пропорцию на пропорцию из уравнения (1):
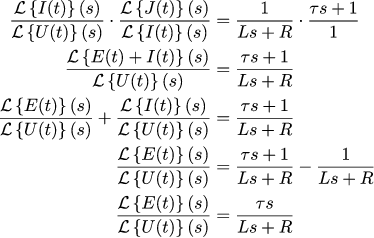
Почти закончили, осталось перейти от координат Лапласа к обычным временным. Для начала раскроем пропорцию:
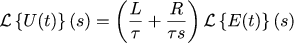
Вооружившись таблицами преобразования Лапласа, можно увидеть следующее:
А это значит, что напряжение U(t) и ошибка задания E(t) должны быть связаны по следующему закону:
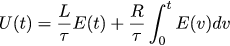
Таким образом, выбрав поведение всей системы как апериодическое звено первого порядка, мы получаем, что необходимый регулятор есть не что иное, как обычный ПИ-регулятор.
Воплощение в жизнь
Сишный код регулятора можно посмотреть тут. Программа вполне стандартная, единственное, что следует отметить, так это то, что у атмеги не хватает здоровья работать с плавающими точками. Поэтому вся работа ведётся с фиксированной точкой и целочисленными переменными.
Проверка работы регулятора
Для проверки работы регулятора зададим ему на вход меандр и синусоидальный сигнал.
Меандр
Вот тут можно взять данные эксперимента: из нулевого начального состояния зададим желаемую силу тока в I0=4А и измерим реально протекающий ток.
Затем давайте посчитаем на бумаге, по какому закону должен изменяться протекающий ток в таких условиях. Это один-в-один совпадает с тем, что мы делали в предыдущей статье:
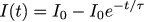
Попробуем подобрать значение параметра, чтобы теоретическая кривая наилучшем образом аппроксимировала реальные данные и сравним с выбранной нами ранее постоянной времени. Код подбора параметра можно взять здесь.
Вот результат работы управляющего контура на полупериоде меандра:
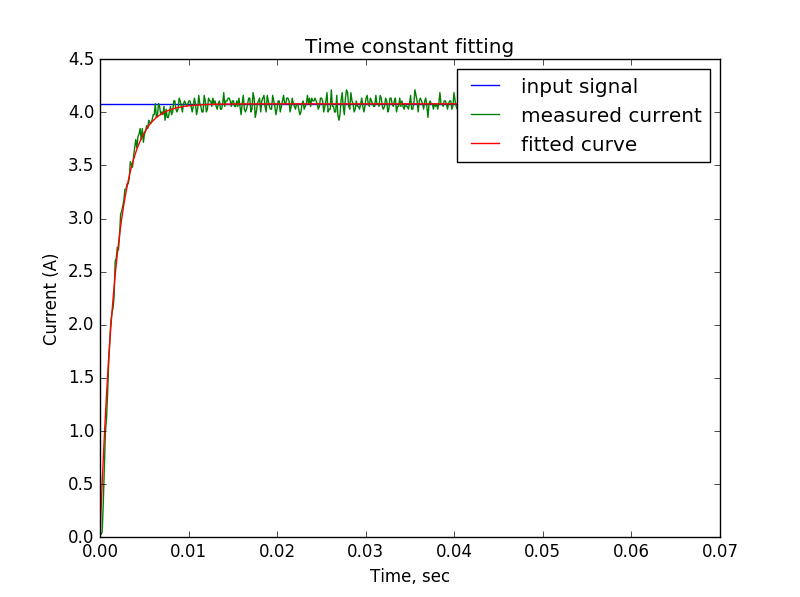
Метод наименьших квадратов нам говорит, что наилучшее значение параметра это .00184, что очень близко к выбранной нами постоянной времени .002. Хорошо видно, что переходный процесс уложился в десять миллисекунд, которые ему были отведены в постановке задачи.
Синусоидальный сигнал
На всякий случай вторая проверка, опять же, вычисления все взяты из предыдущей статьи. При синусоидальном задании силы тока I(t) должна меняться по следующему закону:

Код подбора параметра теоретической кривой можно взять тут. Он нам говорит, что постоянная времени равна .00196, что опять-таки близко к расчётному параметру в 2мс.
Вот результат работы управляющего контура на синусоидальном входном сигнале:

Заключение
В общем, не так страшен чёрт, как его малюют. Большое спасибо arastas за науку! Постараюсь в обозримом будущем найти немного времени, чтобы собрать перевёрнутый маятник не так, как его делал (управляя напряжением), а управляя непосредственно силой тока, это должно упростить расчёты регулятора непосредственно маятника.