Здравствуйте, меня зовут Саша, я написал самый быстрый ресайз изображений для современных х86 процессоров. Я так утверждаю, поскольку все остальные библиотеки, которые я сумел найти и протестировать, оказались медленнее. Я занялся этой задачей, когда работал над оптимизацией ресайза картинок на лету в Uploadcare. Мы решили открыть код и в результате появился проект Pillow-SIMD. Любой желающий с легкостью может использовать его в приложении на языке Python.
Любой код выполняется на конкретном железе и хорошей оптимизации можно добиться, только понимая его архитектуру. Всего я планирую выпустить 4 или 5 статей, в которых расскажу как применять знание архитектуры железа для оптимизации реальной задачи. Своим примером я хочу побудить вас оптимизировать другие прикладные задачи. Первые две статьи выйдут в течение недели, остальные — по мере готовности.
О задаче
Под «ресайзом изображений» я понимаю изменение размеров изображения с помощью ресемплинга методом сверток. Ресемплинг производится над массивом 8-битных RGB пикселей в память, без учета декодирования и кодирования изображений, однако с учетом выделения памяти под конечное изображение и с учетом подготовки коэффициентов, необходимых для конкретной операции.
Вот так строго. Никаких трюков (вроде декодирования из джипега изображения меньшего размера) и никакого комбинирования алгоритмов, только честное измерение работы конкретного алгоритма. Трюки и оптимизации частных случаев можно применить позже, они не предмет рассмотрения этой серии статей.
… с помощью ресемплинга методом сверток. Что?
Чтобы было понятно, что конкретно нуждалось в оптимизации, я расскажу, что такое ресемплинг свертками. Свертка (правильно говорить свертка дискретных значений, т.к. пиксели изображения дискретны) — это очень простая математическая операция. У нас есть какой-то ряд значений №1 (коэффициенты) и ряд значений №2 (данные, в нашем случае интенсивность каналов пикселей). Результат свертки этих двух рядов будет сумма произведений всех членов попарно. Вот так просто — сумма произведений. Матан закончился, не успев начаться.
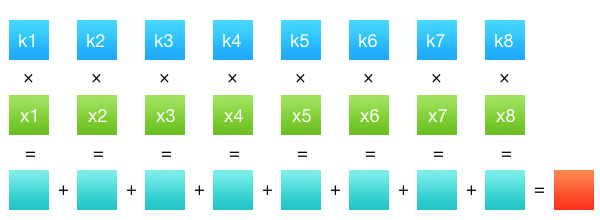
Осталось понять, как именно эта операция связана с ресайзом. Ряд значений №2 — это ряд пикселей исходного изображения. Ряд значений №1 — это коэффициенты, получающиеся из фильтра. Фильтр — это такая функция, которая определяет, как именно мы будем сворачивать значения. Может быть вы замечали в окошке ресайза в Фотошопе или другом графическом редакторе выпадающее меню с фильтрами — билинейный, бикубический, иногда Ланцош. Это и есть этот фильтр. А вот получившееся в результате свертки значение — это интенсивность одного канала одного пикселя конечного изображения. Т.е. чтобы получить изображение размером M×N пикселей, нам нужно сделать M×N×C операций свертки, где С — количество цветовых каналов. Да, посчитать весь пиксель одной операцией не получится, значения разных каналов независимы и должны считаться отдельно.
Функции фильтров не бесконечны, их значения не равны нулю лишь в центральной части: для билинейного фильтра это диапазон значений от –1 до 1; для бикубического от –2 до 2, для Ланцоша от –3 до 3 (правда бывают и другие разновидности Ланцоша).
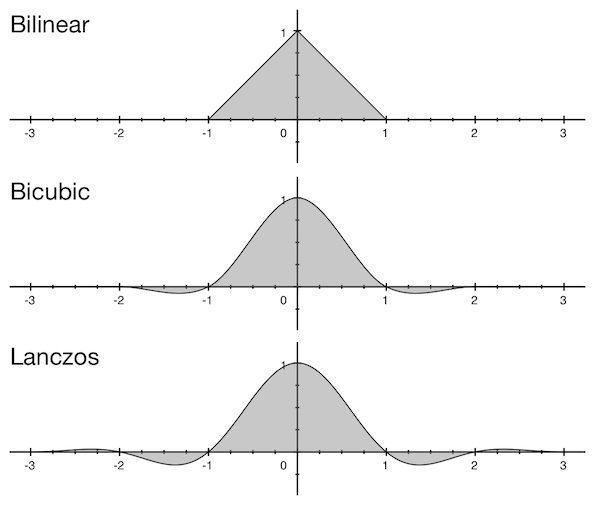
Эти числа называют окном фильтра, т.к. фильтр применяется только в этом диапазоне, а за его пределами равен нулю. Соответственно ряд исходных пикселей, необходимый для свертки, берется в радиусе размером в окно фильтра помноженном на коэффициент уменьшения (или на единицу, если происходит увеличение). Думаю, это лучше объяснить на примере. Нам нужно уменьшить изображение шириной 2560 пикселей до ширины 2048, используя бикубический фильтр. Допустим, мы хотим найти значение 33-го пикселя конечного изображения. У бикубического фильтра размер окна равен двум, а коэффициент уменьшения получается 2560/2048 = 1,25, поэтому нам нужно будет взять строку пикселей исходного изображения от floor((33 - 2) × 1,25) до ceil((33 + 2) × 1,25). Т.е. с 38-го по 44-й пиксель. Для этих же пикселей высчитываются значения коэффициентов.
До этого момента я говорил о ряде коэффициентов и ряде пикселей, упуская из виду факт, что изображение — это вообще-то двумерная структура. И вроде по логике, сворачивать нужно не линию, а какую-то область исходного изображения. Но одно из свойств свёрток заключается в том, что операцию можно провести отдельно по вертикали и по горизонтали, сделав два прохода. Грубо говоря, это позволяет уменьшить сложность одной свертки с O(n²) до O(2n) (на самом деле меньше, но все равно существенно).
Почему все же свертки
Вообще, фраза «ресайз изображения» несет в себе минимум информации о том, что нужно сделать. Она говорит, что мы должны получить изображение конечного размера, используя оригинальное, с сохранением геометрии изображенных объектов. Но использовать исходное изображение можно по-разному. Можно например для каждого конечного пикселя поставить в соответствие один пиксель из исходного и взять его без изменений. Это называется метод ближайшего соседа. Картинка получается грубой, рваной, неприятной:

Так происходит потому, что в конечном изображении была использована очень малая часть исходных пикселей (на приведенном выше примере меньше одного процента). Информацию из тех пикселей, которые не попали в конечное изображение, мы потеряли.
А вот как выглядит ресемплинг с помощью сверток:

Ресемплинг с помощью сверток правильно учитывает вклад каждого исходного пикселя в конечное изображение. Он универсален, т.к. дает одинаково хороший и предсказуемый результат для широкого диапазона коэффициентов масштабирования, не содержит искажений геометрии на локальном уровне (с оговоркой, что используется фильтр, не дающий таких искажений, т.к. некоторые фильтры все же дают). И вообще, он весь такой правильный и хороший со всех сторон, кроме одной: производительности.
Pillow
Pillow — это библиотека для работы с изображениями на языке Python, развиваемая сообществом во главе с Alex Clark и Eric Soroos. В Uploadcare Pillow использовался еще до того, как я пришёл в команду. Тогда мне это показалось странным — работа с изображениями была одной из основных задач, зачем было брать для нее библиотеку, завязанную на язык. Не лучше ли взять тот же ImageMagick, у которого тонна функций, которым пользуются миллион разработчиков, уж в нем наверняка все должно быть хорошо с производительностью. По прошествии нескольких лет, могу сказать, что это была удача как для меня, так и для Pillow. Как выяснилось, производительность обеих библиотек на старте была примерно одинаковой, но я очень сомневаюсь, что у меня хватило бы сил сделать для ImageMagick что-то такое, что я сделал для Pillow.
Pillow — это форк очень старой библиотеки PIL. Исторически, для ресайза в PIL не использовались свёртки. Первая реализация ресайза на свёртках в PIL появилась в версии 1.1.3 и была доступна при использовании фильтра ANTIALIAS, название которого подчеркивало то, что остальные фильтры использовали менее качественные алгоритмы. В сети до сих пор можно часто встретить уже не актуальные рекомендации использовать при ресайзе в PIL (и в Pillow, как приемнике) только фильтр ANTIALIAS.
К сожалению, у ANTIALIAS была довольно низкая производительность. Я полез в исходный код, чтобы посмотреть, что можно сделать, и оказалось, что реализация ресайза для ANTIALIAS (то есть свертки), может быть использована и с остальными фильтрами. А сама константа ANTIALIAS соответствует фильтру Ланцоша, у которого большое окно (±3), и поэтому он достаточно медленный. Самая первая оптимизация, которую я хотел сделать — включить свёртки для билинейного и бикубического фильтров. Так стало бы возможным у себя в приложении использовать более дешёвый бикубический фильтр (с окном ±2) и не слишком потерять в качестве.
Дальше мне было интересно посмотреть на код самого ресайза. Я без труда нашёл его в этом модуле. И хоть я и пишу в основном на питоне, я сразу заметил несколько сомнительных мест с точки зрения производительности. После нескольких оптимизация я получил прирост в 2,5 раза (это будет описано в следующей статье). Потом я стал экспериментировать с SIMD, переводить все вычисления на целые числа, агрессивно разворачивать циклы и группировать вычисления. Задача была чрезвычайно интересной, в голове всегда были еще пара идей, как улучшить производительность. Я погружался в кроличью нору все глубже и глубже, периодически проверяя очередную гипотезу.
Постепенно код становился все больше, а скорость все выше. Часть наработок отдавалась обратно в Pillow. Но SIMD-код было трудно перенести, потому что он написан для конкретной архитектуры, а Pillow — кроссплатформенная библиотека. Поэтому было решено сделать не кроссплатформенный форк Pillow-SIMD. Версии Pillow-SIMD полностью соответствуют версиям оригинальной Pillow и добавляют ускорение некоторых операций.
В последних версиях Pillow-SIMD с AVX2 ресайз работает от 15 до 30 раз быстрее, чем в первоначальном PIL. Как я уже говорил в самом начале, это самая быстрая реализация качественного ресайза, которую мне удавалось протестировать. Можно посмотреть страничку, на которой собраны результаты бенчмарков разных библиотек.
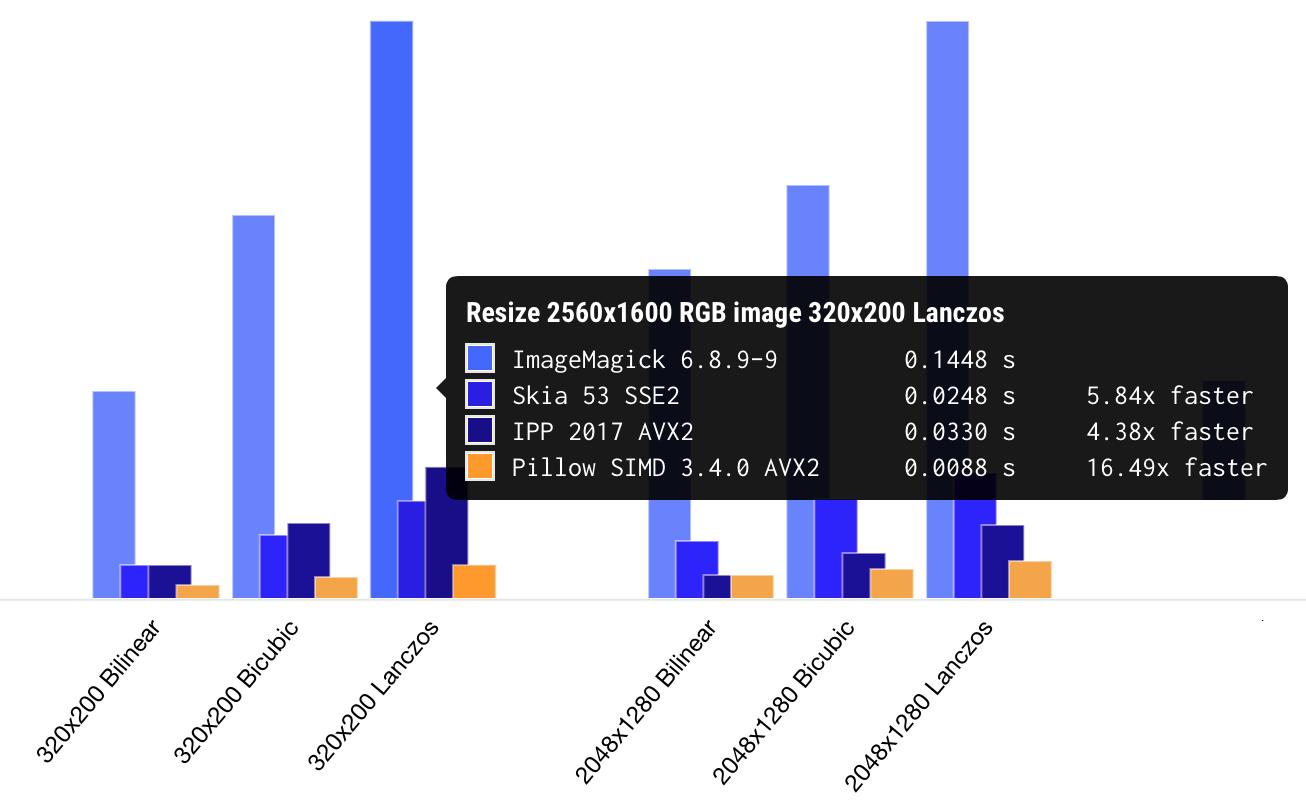
Что меня радует в случае с Pillow и Pillow-SIMD, это то, что это реальные библиотеки, которые реально использовать даже начинающему разработчику. Это не кусок кода, опубликованный на Stack Overflow, который непонятно куда воткнуть. И не «примитивные блоки», из которых как из конструктора нужно собирать каждую операцию. И даже не сложная C++ библиотека с запутанным интерфейсом, которая компилируется полчаса. Это одна строчка установки, одна строчка импорта библиотеки, одна строчка загрузки изображения и, «эй, мам, смотри, я пользуюсь самым быстрым ресайзом в своем приложении».
Замеры производительности
В статьях я буду выкладывать замеры производительности в виде таблицы, в которой исходное изображение разрешением 2560×1600 пикселей ресайзится до разрешений 320x200, 2048x1280 и 5478x3424 с использованием билинейного, бикубического и фильтра Ланцоша (т.е. всего 9 операций). Исходное изображение взято достаточно большое, чтобы не поместиться полностью в кеш процессора третьего уровня. При этом фактическое содержимое изображения не имеет значения с точки зрения производительности, можно ресайзить хоть пустой белый лист, хоть черный, хоть фоточку вашего кота. Вот пример результатов библиотеки Pillow версии 2.6, до любых оптимизаций.
Scale 2560×1600 RGB image
to 320x200 bil 0.08927 s 45.88 Mpx/s
to 320x200 bic 0.13073 s 31.33 Mpx/s
to 320x200 lzs 0.16436 s 24.92 Mpx/s
to 2048x1280 bil 0.40833 s 10.03 Mpx/s
to 2048x1280 bic 0.45507 s 9.00 Mpx/s
to 2048x1280 lzs 0.52855 s 7.75 Mpx/s
to 5478x3424 bil 1.49024 s 2.75 Mpx/s
to 5478x3424 bic 1.84503 s 2.22 Mpx/s
to 5478x3424 lzs 2.04901 s 2.00 Mpx/sВторой столбец здесь это время в секундах, а третий — пропускная способность исходного изображения для данной операции. То есть, если операция заняла 0,2 с, то пропускная способность будет 2560×1600/0,2 = 20,48 мегапикселей в секунду.
Исходное изображение ресайзится до разрешения 320×200 за 164 миллисекунды. Ну что, вроде неплохо. Может быть вообще не нужно оптимизировать, оставить как есть? Ну, если вспомнить, что разрешение фоток с мобильных телефонов сейчас в среднем имеет размер 12 мегапикселей, то все получается не так радужно. Фотка с айфона будет уменьшаться полсекунды без учета распаковки. Учитывая другие операции, в минуту вы можете обработать ≈80 картинок, а в час — около 5000. Текущая нагрузка на наш сервис около 130 тысяч запросов в час. Нам бы понадобилось 26 AWS c4.large серверов, работающих на пределе, чтобы справиться с такой нагрузкой. В реальности же у нас задействовано всего 4 сервера, нагрузка на которые в горячие часы около 40%.
Если бы такой эффект удалось экстраполировать до масштабов планеты и заменить весь код, занимающийся ресайзом картинок, на более эффективный, польза была бы огромной. Десятки тысяч сэкономленных серверов, сотни киловатт электричества. А это уже одна миллионная от мирового потребления. Да можно было бы спасти планету!
Дальше: Часть 1, общие оптимизации