Comments 46
К этой задаче есть дополнение — когда добавлять сахар в чай если надо: а) погорячее, б) похолоднее
Или сливки в кофе.
На сколько я знаю, у сахара отрицательная теплота растворения. То есть растворяясь он охлаждает.
да, и в этом нюанс школьной задачи. Подобная же задача про какой стакан остынет быстрее с чайной ложкой ли без.
Если ложка пластиковая, то без разницы.
Не «без разницы» а «без видимого эффекта». Конечно разница будет. Тем более, как мы уже поняли из статьи, ложка может быть большая по площади а снаружи, например, жидкий азот.
Уточню — «без существенной разницы». Я, разумеется, в курсе что всякая физическая задача бесконечно сложна, потому что на всякое физическое тело действуют одновременно все законы физики. В том числе и еще не открытые.
Задача про яблоко — это шедевр! Спасибо за ссылку.
Если понравилось, тогда советую всю книгу прочитать.
ложка может быть большая по площади а снаружи, например, жидкий азот.И начались «урановые ломы» :)
У меня кстати похожий вопрос. Отключили горячую воду. Вы нагреваете чайник воды и выливаете в таз. Мыться вы начнете через 5 минут. Есть два варианта — сразу добавить холодной воды или через 5 минут.
В каком варианте потеряется меньше тепла? Если воды добавить сразу, то будет меньше разница температур с окружающей средой и по идее медленнее будет теплоперенос.
В каком варианте потеряется меньше тепла? Если воды добавить сразу, то будет меньше разница температур с окружающей средой и по идее медленнее будет теплоперенос.
Этот эксперимент на практике просто невозможно проделать. Остается довольствоваться только одной теорией.
А эти формулы учитывают все три канала передачи тепла: конвекцию, излучение и испарение?
Нет такой формы передачи тепла как испарение. Учитывается только кондуктивная передача тепла.
А разве с верхней поверхности не происходит испарение?
И разве испарение не сопровождается понижением температуры жидкости?
И разве испарение не сопровождается понижением температуры жидкости?
Все верно, но фундаментальных способов обмена теплом три: конвенкция, излучение, теплопроводность. Испаряясь, вода теряет энергию за счет всех трёх. Пар поднимается вверх, так как теплее (конвенкция), излучает, по той же причине, и обменивается с воздухом кондуктивно, так как соприкасается с ним непосредственно. Если говорить об испарении, необходимо учесть влажность воздуха (во влажном испарение замедляется), давление (при низком испарение интенсивнее), а также обдув (при обдуве испарение интенсивнее). Верно кто-то здесь подметил, что физическая задача бесконечно сложна, и все-все учесть крайне сложно.
Вот и я про то же: после смешивания мы имеем одно зеркало испарения. И скорость потери тепла от испарения будет сильно зависеть от: влажности, температуры, скорости движения окружающего воздуха.
И мне кажется, что испарение может вносить заметный вклад в теплопотери стакана.
Плюс влияние размеров стакана — при одних его пропорциях в жидкости разовьется естественная конвекция и теплота будет переноситься от внутренних горячих слоев к холодным стенкам, а при других конвекция может и не возникнуть.
Плюс влияние размеров стакана — при одних его пропорциях в жидкости разовьется естественная конвекция и теплота будет переноситься от внутренних горячих слоев к холодным стенкам, а при других конвекция может и не возникнуть.
Следующая задача на практически ту же тему:
На плите кипящая кастрюля (100°, 1 литр воды).
Нам требуется два литра кипятка. Варианты: долить в кастрюлю (вместимости хватит) один литр холодной и дождаться кипения, либо взять еще одну кастрюлю, налить туда литр холодной воды и поставить на конфорку рядом.
Если пренебрегать теплоотдачей и краевыми эффектами нагревания самой кастрюли, то варианты эквивалентны.
Но в свое время я на спор попытался доказать теорию практикой и с треском проиграл человеку, который у плиты проводил времени больше чем я, но совершенно не знал физику.
На плите кипящая кастрюля (100°, 1 литр воды).
Нам требуется два литра кипятка. Варианты: долить в кастрюлю (вместимости хватит) один литр холодной и дождаться кипения, либо взять еще одну кастрюлю, налить туда литр холодной воды и поставить на конфорку рядом.
Если пренебрегать теплоотдачей и краевыми эффектами нагревания самой кастрюли, то варианты эквивалентны.
Но в свое время я на спор попытался доказать теорию практикой и с треском проиграл человеку, который у плиты проводил времени больше чем я, но совершенно не знал физику.
И что быстрее получается?
Я бы (пока без особой физики) поставил на литр холодной рядом, поскольку разница между пламенем комфорки и водой будет больше, соответственно передача тепла — быстрее. И, в этом случае, греть будут две комфорки — левая будет поддерживать температуру кипятка (который достаточно много тепла отдает), а правая — нагревать свежий кипяток.
Я бы (пока без особой физики) поставил на литр холодной рядом, поскольку разница между пламенем комфорки и водой будет больше, соответственно передача тепла — быстрее. И, в этом случае, греть будут две комфорки — левая будет поддерживать температуру кипятка (который достаточно много тепла отдает), а правая — нагревать свежий кипяток.
Я так понял что комфорка всегда одна. Либо холодная вода греется с кипятком, либо кипяток простаивает, пока холодная греется отдельно. иначе ответ очевиден.
Ответ вовсе не очевиден. Попробуйте в домашних условиях.
Хотя нужны две одинаковые кастрюли и две одинаковые конфорки.
Обе конфорки нагреты, на одной в кастрюле варится литр кипятка, в руках у вас еще два раза по литру.
Правой рукой выливаем воду в кипяток, левой рукой — в пустую кастрюлю поставленную на конфорку.
Смотрим что быстрее закипит :)
(Ну, можно обойтись одной кастрюлей, одной конфоркой и секундомером)
В конце же концов нас интересует не квадратный конь в стерильных условиях. А практическое решение прикладных задач. Что толку от всего матана, если чашечка кофе с молоком будет остывать быстрее/медленнее пока официант её несет к столику чем отдельно тот же кофе и то же молоко по отдельности?
Хотя нужны две одинаковые кастрюли и две одинаковые конфорки.
Обе конфорки нагреты, на одной в кастрюле варится литр кипятка, в руках у вас еще два раза по литру.
Правой рукой выливаем воду в кипяток, левой рукой — в пустую кастрюлю поставленную на конфорку.
Смотрим что быстрее закипит :)
(Ну, можно обойтись одной кастрюлей, одной конфоркой и секундомером)
В конце же концов нас интересует не квадратный конь в стерильных условиях. А практическое решение прикладных задач. Что толку от всего матана, если чашечка кофе с молоком будет остывать быстрее/медленнее пока официант её несет к столику чем отдельно тот же кофе и то же молоко по отдельности?
Условия интересные, нужно подумать. Решая подобные задачи, никто не требует от вас ответа с 5-ой цифрой после запятой. Важно уловить взаимосвязи. Вы должны понять что от чего зависит и на сколько. Уверен, выводы можно применить ко многим практическим вопросам, не ограничиваясь лишь чашечкой кофе.
в пустую кастрюлю поставленную на конфорку.важный момент в том, нагрета ли до 100+ градусов пустая кастрюля.
Если цель — быстрее получить кипяток, то нужно налить часть холодной воды в горячую, оставшуюся холодную поставить на вторую конфорку. Разделить нужно с таким расчётом, чтобы обе кастрюльки закипели одновременно. Считать лень, но думаю поделить нужно примерно пополам, так как при высокой температуре пламени можно приблизительно считать скорость нагрева равномерной.
Мне кажется, что добавив холодную воду в кипяток — это выигрышный вариант, поскольку перемешиваясь, вода очень быстро примет среднюю температуру, так как площадь передачи тепла безумно большая.
А вот грея литр холодной воды в соседней кастрюле — это долго. Даже если кастрюля будет раскалена добела — не хватит её теплопроводности по сравнению со смешиванием.
А вот грея литр холодной воды в соседней кастрюле — это долго. Даже если кастрюля будет раскалена добела — не хватит её теплопроводности по сравнению со смешиванием.
Идея в том, чтобы разделить один долгий процесс на два более коротких и идущих параллельно. У нас две конфорки, но если смешать всё, то работать будет только одна, грея 2 литра тёплой воды. Если не смешивать совсем, то одна конфорка будет перегружена, грея литр холодной, а другая будет работать вхолостую, грея и так горячую воду. Если разделить, то обе конфорки будут задействованы — одна будет греть ~1.5 литра тёплой, другая ~0.5л холодной. Оптимум — обе конфорки заканчивают греть свои кастрюльки за одно и то же время.
Имхо, долив и нагрев будет быстрее, чем нагрев в другой емкости с нуля. Емнип, объемная теплоемкость воды понижается с ростом температуры.
Кастрюля с двумя литрами — 11:45
Прогретая кастрюля с одним литром — 9:20
Сложно определить, что такое кипение. Когда в кастрюле с одним литром поверхность уже бурлила, в кастрюле с двумя литрами, при похожем состоянии дна, пузыри никак не могли добраться до поверхности, поглощаясь водой.
Прогретая кастрюля с одним литром — 9:20
Сложно определить, что такое кипение. Когда в кастрюле с одним литром поверхность уже бурлила, в кастрюле с двумя литрами, при похожем состоянии дна, пузыри никак не могли добраться до поверхности, поглощаясь водой.
k = k_s + k_b + k_t
Это неочевидно.
Тут. В двух словах, потеря тепла через дно, боковые стенки и поверхность происходит параллельно (независимо). Вот если бы сначала теплообмен шел через дно, потом через боковую стенку и затем поверхность, формула была бы: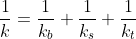 
Вместо кучи формул нарисовали бы лучше один график — статья бы от этого выиграла намного.
Где матан?
а можно автора попросить в конце статьи все-таки написать практический вывод, соответствующий поставленному условию в задаче (ну как в школе учили):
Например, можно указать, что при исходной температуре холодной в 15, кипятка 95 и комнатной 20 получается, что холоднее будет смесь, приготовленная через 10 минут, а не «ранняя».
вот здесь уже почти «наклевался» сколь-нибудь практический вывод.
В идеале, как писали выше, увидеть бы графики для сколь-нибудь стандарнтых значений, например, 15 vs 100 и при какой температуре окружающей среды получается перелом.
Т.е., после этого можно будет с чистой совестью говорить, что «в домашних условиях, с если нужно сохранить температуру, более выгодно смешивать раньше, чем позже»
Вопрос: в какой смеси вода будет горячее?Хотелось бы где-то в пределах "Таким образом" и "А на самом деле..?" увидеть что-то более конкретное, чем ΔT и e.
Например, можно указать, что при исходной температуре холодной в 15, кипятка 95 и комнатной 20 получается, что холоднее будет смесь, приготовленная через 10 минут, а не «ранняя».
ввиду того что горячая вода чаще всего «горячее» чем холодная «холоднее» относительно комнатной температуры
вот здесь уже почти «наклевался» сколь-нибудь практический вывод.
В идеале, как писали выше, увидеть бы графики для сколь-нибудь стандарнтых значений, например, 15 vs 100 и при какой температуре окружающей среды получается перелом.
Т.е., после этого можно будет с чистой совестью говорить, что «в домашних условиях, с если нужно сохранить температуру, более выгодно смешивать раньше, чем позже»
К примеру 15 vs 100. (15+100)/2 = 57.5 — температура перелома. Таким образом если комнатная 25 градусов (25 < 57.5), ранняя смесь будет теплее. Если комнатная 60 градусов (60 > 57.5) — смесь приготовленная через 10 мин.
Сорри за некропост, но вывод из статьи не очень соответствует задаче.
В самом начале, просто указаны два стакана, почти питьевые, и «горячая» и «холодная» — без указания температур стаканов и окружающей среды.
Поэтому напрашиваются логичные дефолтные условия — горячая вода — например кипяток или горячая вода из крана (50-70 градусов), а холодная — околокомнатной температуры, в условиях обычной комнаты.
В стандартной ситуации, без всяких формул понятно, что в первом стакане вода будет горячее, поскольку она сразу смешивается, и общая площадь поверхности соприкосновения воды с окружающей средой меньше, чем у второго стакана, где две половинки остывали отдельно, обладая «дополнительной стороной» соприкосновения с окружающей средой.
Но когда в конечном счете сделаны выводы на основании кучи формул и внезапном ВВОДЕ новых дополнительных условий — как-то не очень комильфо.
В самом начале, просто указаны два стакана, почти питьевые, и «горячая» и «холодная» — без указания температур стаканов и окружающей среды.
Поэтому напрашиваются логичные дефолтные условия — горячая вода — например кипяток или горячая вода из крана (50-70 градусов), а холодная — околокомнатной температуры, в условиях обычной комнаты.
В стандартной ситуации, без всяких формул понятно, что в первом стакане вода будет горячее, поскольку она сразу смешивается, и общая площадь поверхности соприкосновения воды с окружающей средой меньше, чем у второго стакана, где две половинки остывали отдельно, обладая «дополнительной стороной» соприкосновения с окружающей средой.
Но когда в конечном счете сделаны выводы на основании кучи формул и внезапном ВВОДЕ новых дополнительных условий — как-то не очень комильфо.
под катом «интересненькое» ошибка в том переходе, где появляется sqrt(e):
sqrt(e) * exp(-k deltat) — это не exp(-1/2 k deltat), а exp(-k deltat + 1/2)
sqrt(e) * exp(-k deltat) — это не exp(-1/2 k deltat), а exp(-k deltat + 1/2)
Sign up to leave a comment.
Задача про четыре стакана