Хотите озадачить начинающего шахматиста?
Попросите его поставить мат конём и слоном.
Хотите озадачить начинающего программиста?
Попросите его рассчитать мат конём и слоном.

Шахматные задачи будоражат воображение программиста,
именно поэтому для практической демонстрации комбинаторики
я выбрал самую сложную шахматную задачу из цикла «мат одинокому королю».
Цель проекта — создать базу решений, то есть список правильных ходов для всех возможных расположений белого короля, слона, коня и чёрного короля на шахматной доске.
В этой публикации я расскажу, как я решал эту задачу, с какими сложностями пришлось столкнуться, а также продемонстрировать, что в итоге получилось. Используемые технологии: C#, JavaScript, PHP, HTML, CSS.
Будучи весьма посредственным шахматистом, я так и не научился быстро ставить мат конём и слоном. Поэтому я решил компенсировать этот недостаток своими навыками программирования, перебрать все возможные позиции и найти для каждой правильный ход.
Прежде чем написать хоть строчку кода, я несколько недель вынашивал «наполеоновский» план, как я это буду делать. Мне очень хотелось начать решать эту задачу с конца, с перебора всех матовых комбинаций. А потом делать по одному ходу назад, пока не будут исчерпаны все возможные варианты.
На шахматной доске 64 клетки. У нас четыре фигуры.
Количество возможных комбинаций — 64 * 64 * 64 * 64 = 16,777,216.
Можно оставить только белопольного слона.
Количество вариантов уменьшится вдвое: 64 * 32 * 64 * 64 = 8,388,608.
Именно столько позиций будет в нашей базе решений.
На самом деле комбинаций ещё меньше: на одной клетке не может стоять две фигуры, короли не могут стоять на соседних клетках, чёрный король не может быть под шахом и так далее. Забегая вперёд скажу, что в базе решений оказалось 5,609,790 комбинаций, массив будет заполнен на 67%.
Однако для упрощения алгоритма и ускорения доступа к данным базы я решил «не мелочиться» и создать четырёхмерный массив для всех комбинаций.
Для хранения каждой комбинации определена такая структура:
Внутри используется ещё одна структура Coord для записи координат фигуры, с возможностью вычисления индекса от 0 до 63, а также с перегруженным оператором сравнения.
Эта структура оказалась очень удобной для передачи в качестве аргумента в различные вспомогательные функции, например:
Однако для записи результата базы решений этой структуры не достаточно, ещё нам потребуется…
Целью нашей программы будет создание «белого ящика», в который будут складываться все позиции, в которых «ход белых», и для которых известно — какой именно ход нужно делать, и через сколько ходов будет гарантированно поставлен мат.
Составной частью «белого ящика» является следующая структура:
Для организации «белого ящика» проще всего открыть четырёхмерную матрицу. Каждая размерность этой матрицы соответствует возможной позиции каждой фигуры:
первая размерность — координата белого короля.
вторая размерность — координата белого слона / 2.
третья размерность — координата белого коня.
четвёртая размерность — координата чёрного короля.
Главное — не перепутать их порядок :) Массив получится на 33% разряженным, но уж очень удобным для обработки. Именно в этом массиве будет храниться 8,388,608 записей для решения комбинаций.
Кстати, прежде чем начать писать все алгоритмы перебора, я создал пустой проект и проинициализировал эту четырёхмерную матрицу, дабы убедиться, что памяти хватит и не надо будет что-то дополнительное изобретать. Видимо, сказался опыт участия в олимпиадах по информатике прошлого тысячелетия, где размер структуры не мог превышать 64 килобайт, ибо Turbo Pascal 7.0.
Кратко опишу основную идею решения этой задачи. В основу взят алгоритм поиска вширь, который пришлось немного доработать, так как в шахматы играют двое и ходы делаются по очереди. Поэтому вместо одной очереди нам потребуется две — «чёрная» и «белая».
Со структурой WhitesMove мы уже познакомились. Структура BlacksMove немного проще, так как в ней нет надобности хранить последний ход чёрных.
Сначала в «чёрную очередь» мы разместим все матовые позиции, в которых ход чёрных. Потом из каждой такой позиции будем делать обратный ход за белых и формировать «белую очередь» — список позиций, в которых ход белых.
Эти действия нужно будет повторять до полного исчерпания всех возможных комбинаций.
Основной алгоритм в виде псевдокода:
Создание базы правильных ходов начинается с поиска всех матовых комбинаций. Использование енумераторов ��озволило достаточно эффектно описать этот процесс.
Всего найдено 232 матовые позиции. Напомню, что мы ограничились только белопольным слоном.
Некоторые из них достаточно экзотические, не существующие и «кооперативные», это когда чёрный король сам полез под мат.
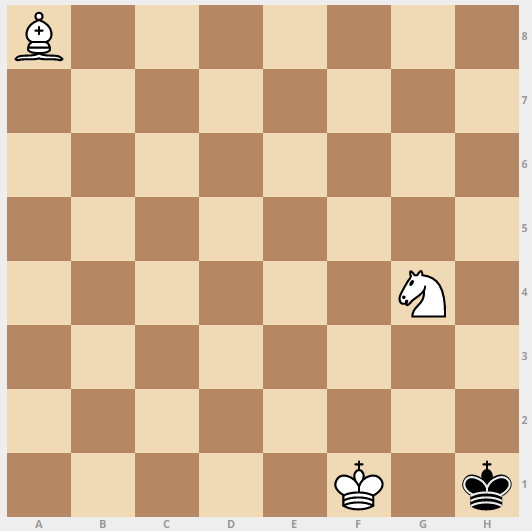
Шахматистам хорошо известно, что мат конём и белопольным слоном нужно ставить в белом углу. В чёрном углу мат возможен только если чёрные будут подыгрывать. Я специально разместил фото с именно таким псевдоматом в начале статьи, чтобы спровоцировать внимание настоящих шахматистов :)
Следующий этап — сделать обратный ход белых. То есть, для каждой найденной матовой позиции сделать все возможные обратные ходы белых.
Как сделать обратный ход? Учитывая, что взятия в наших позициях не предусмотрены, алгоритм достаточно простой — сделать любой ход белых, после которого не будет шаха чёрному королю.
Все найденные таким образом позиции можно уже складывать в «белый ящик», указывая, что до мата один ход, и какой именно ход для этого нужно сделать. Попутно помещаем найденные комбинации в «чёрную очередь».
Вот как выглядит эта часть алгоритма:
Всего было найдено 920 таких позиций, вот самые интересные:
Ход конём:



Ход слоном:
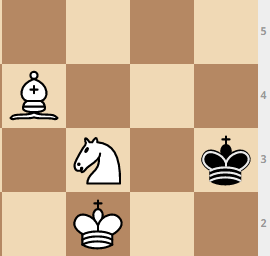

Ход королём:

Следующий этап — сделать обратный ход чёрных. С этим алгоритмом я провозился дольше всего, было сделано немало ошибок, прежде чем всё заработало верно.
На первый взгляд, всё аналогично предыдущему варианту: для каждой позиции из «белой очереди» необходимо перебрать все возможные ходы чёрного короля. И добавлять все найденные комбинации в «чёрную очередь» — ведь это мат в полтора хода, от которого можно будет потом снова делать обратный ход за белых — будет мат в два хода — и так продолжать, пока не будут пересмотрены все варианты.
В этом и была ошибка. При любом возможном ходе чёрных получается «кооперативный» мат в полтора хода, а на самом деле король не обязательно будет идти под мат. Указал мне на эту ошибку Дмитрий Гринь, который посещал все мои вебинары по созданию этой программы, за что ему отдельное спасибо.
Правильный алгоритм следующий: для каждой позиции N после обратного хода чёрного короля нужно перебрать все возможные его прямые ходы, чтобы убедиться, что все они ведут к знакомым позициям из «белого ящика», то есть ведут к мату. И только после этого позицию N можно добавлять в «чёрную очередь». А если из позиции N чёрный король может «улизнуть», то такой вариант пропускаем. Она встретится на последующих итерациях, когда знакомых позиций будет больше.
Вот как выглядит эта часть алгоритма:
Всего было найдено 156 комбинаций «Мат в полтора хода».
Описанные алгоритмы создания полуходов необходимо зациклить. Из «чёрной очереди» мы формируем «белую очередь», а потом наоборот — из «белой» формируем «чёрную». И так до тех пор, пока не будут исчерпаны все новые позиции. «Белая коробка» заполняется на этапе формирования «белой очереди», так как в неё помещаются позиции, в которых ход белых.
Готовый алгоритм перебора всех вариантов отработал где-то за 12 минут и остановился на 33 ходу. Именно столько максимум ходов нужно, чтобы заматовать чёрного короля конём и слоном из любой позиции.
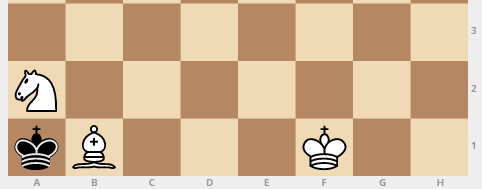
Кстати, таких «самых сложных» позиций оказалось не так много, всего 156, вот одна из них:

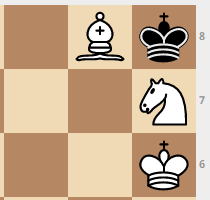
Есть немало позиций, в которых даже после хода белых чёрный король может съесть коня или слона и выйти на ничью. Также есть патовые варианты. Вот несколько самых интересных позиций.


Каким способом хранить найденную базу решений?
Самый простой и неправильный способ — использовать сериализацию. Засериализованный четырёхмерный массив структуры занял 1.7 гигабайта(!) на диске. Процесс сериализации длился минут шесть, на десериализацию потребовалось примерно столько же.
Такой вариант, ясное дело, не подходит. К тому же, на практике нет надобности использовать весь четырёхмерный массив. Для конкретной позиции нужна только одна запись.
Эврика! Для экономии места ещё можно избавиться от хранения координат фигур для каждой комбинации. Когда у нас есть четырёхмерный массив, то позиция каждой фигуры на доске однозначно определяется её индексом в массиве.
Было решено хранить всю базу решений в одном файле — как линейную развёртку четырёхмерного массива. Для любой возможной позиции вычисляется адрес, по которому записан правильный ответ.
Как максимально компактно записать нужный нам ответ? Позицию фигур хранить не надо, поэтому остаётся только три числа — сколько ходов до мата, чем ходить и куда ходить. Именно так однозначно определяется правильный ход за белых.
6 бит. Сколько ходов до мата — это целое число от 0 до 33.
2 бита. Какая фигура ходит — три возможных варианта, король, слон или конь.
6 бит. Куда фигура ходит — индекс поля на доске от 0 до 63.
Значит, на каждую запись решения достаточно два байта:
1 байт — сколько ходов до мата, или 0, если позиция незнакомая.
2 байт — FFNNNNNN
FF — номер фигуры, которой нужно ходить (1 — король, 2 — слон, 3 — конь)
NNNNNN — координата клетки — куда ходить (от 0 до 63).
Итак, файл базы решений занимает 64 * 32 * 64 * 64 слов = ровно 16 мегабайт. Размещение фигур задаётся координатами каждого слова, в первом байте — количество ходов до мата (или 0 если решения нет), во втором байте хранится правильный ход.
Можно было бы ещё в два раза уменьшить размер файла, если не хранить количество ходов до мата, но так играть будет не интересно.
Пришло время платить за оптимизацию. Нужно реализовать алгоритм пересчёта координат для комбинаций с «чёрно-белым» слоном.
Это было сделано следующим образом. Если координата слона попадает на чёрное поле, то необходимо координаты всех фигур на доске «перевернуть». При этом координата Y остаётся неизменной, а X меняется на 7-X. Наглядная демонстрация переворота координат см. на рисунке.
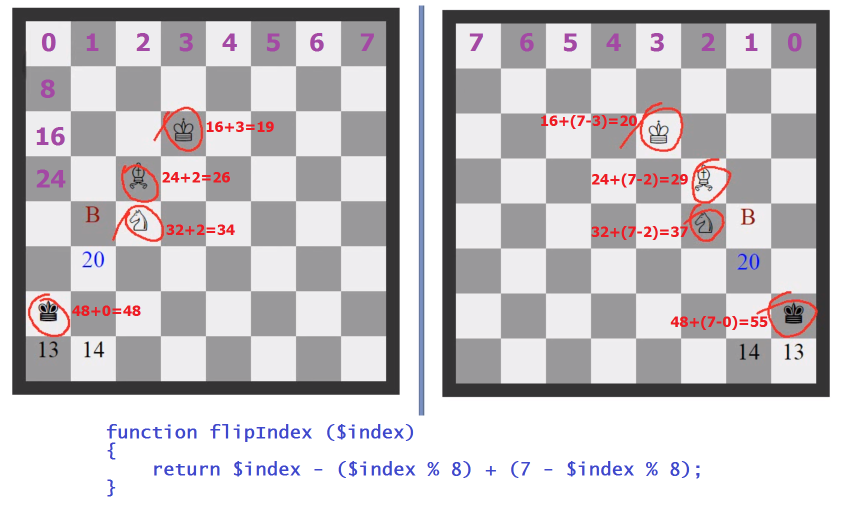
Если слон стоит на белой клетке, то сначала необходимо «перевернуть» координаты всех фигур. Потом искать позицию в ба��е решений. И ещё раз «перевернуть» считанную оттуда координату правильного хода.
Итак, Задача решена!
База решений создана.
Но как её продемонстрировать?
Самый наглядный способ — использовать web-технологии, чтобы можно было просто дать ссылку на работающий пример. На моей «формуле программиста» уже был создан фотокурс "Нано-шахматы", где с использованием технологий HTML, CSS, JavaScript и PHP была создана интерактивная шахматная доска для игры вдвоём без правил. Именно этот скрипт был взят за основу.
Я оставил только четыре фигуры, убрал возможность взятия, добавил РНР-функции для считывания правильных ходов из базы решений и «вдохнул жизнь» через JavaScript.
На странице www.videosharp.info/chess вы можете поэкспериментировать с базой решений.

Для каждой позиции рассчитываются ходы как за белых, так и за чёрных.
За белых — лучший ход, который ведёт к мату.
За чёрных — сколько ходов до мата на любой возможный ход.
Мышкой можно делать любые перемещения фигур, не обязательно по правилам.
Скрипт рассчитает вариант для любой позиции, либо напишет, что вариантов нет.
Интересно поиграть, выполняя предложенные ходы или передвигая фигуры на своё усмотрение.
Была проделана большая, интересная работа по решению шахматной задачи.
Если вы желаете повторить этот путь — можете посмотреть видеозаписи по созданию этой программы с нуля до результата с подробными пояснениями и самостоятельными заданиями.
Желаю удачи!
Попросите его поставить мат конём и слоном.
Хотите озадачить начинающего программиста?
Попросите его рассчитать мат конём и слоном.

Шахматные задачи будоражат воображение программиста,
именно поэтому для практической демонстрации комбинаторики
я выбрал самую сложную шахматную задачу из цикла «мат одинокому королю».
Постановка цели
Цель проекта — создать базу решений, то есть список правильных ходов для всех возможных расположений белого короля, слона, коня и чёрного короля на шахматной доске.
В этой публикации я расскажу, как я решал эту задачу, с какими сложностями пришлось столкнуться, а также продемонстрировать, что в итоге получилось. Используемые технологии: C#, JavaScript, PHP, HTML, CSS.
Будучи весьма посредственным шахматистом, я так и не научился быстро ставить мат конём и слоном. Поэтому я решил компенсировать этот недостаток своими навыками программирования, перебрать все возможные позиции и найти для каждой правильный ход.
Прежде чем написать хоть строчку кода, я несколько недель вынашивал «наполеоновский» план, как я это буду делать. Мне очень хотелось начать решать эту задачу с конца, с перебора всех матовых комбинаций. А потом делать по одному ходу назад, пока не будут исчерпаны все возможные варианты.
Сколько всего вариантов?
На шахматной доске 64 клетки. У нас четыре фигуры.
Количество возможных комбинаций — 64 * 64 * 64 * 64 = 16,777,216.
Можно оставить только белопольного слона.
Количество вариантов уменьшится вдвое: 64 * 32 * 64 * 64 = 8,388,608.
Именно столько позиций будет в нашей базе решений.
На самом деле комбинаций ещё меньше: на одной клетке не может стоять две фигуры, короли не могут стоять на соседних клетках, чёрный король не может быть под шахом и так далее. Забегая вперёд скажу, что в базе решений оказалось 5,609,790 комбинаций, массив будет заполнен на 67%.
Однако для упрощения алгоритма и ускорения доступа к данным базы я решил «не мелочиться» и создать четырёхмерный массив для всех комбинаций.
Для хранения каждой комбинации определена такая структура:
struct Combo
{
public Coord whiteKing;
public Coord whiteBishop;
public Coord whiteKnight;
public Coord blackKing;
}
Внутри используется ещё одна структура Coord для записи координат фигуры, с возможностью вычисления индекса от 0 до 63, а также с перегруженным оператором сравнения.
public struct Coord
{
public byte x; // шахматная вертикаль от 0 до 7 (от a до h)
public byte y; // шахматная горизонталь от 0 до 7
public int index
{
get { return x + y * 8; }
set { x = (byte) (value % 8);
y = (byte) (value / 8); }
}
public static bool operator == (Coord a, Coord b)
{
return a.x == b.x && a.y == b.y;
}
}
Эта структура оказалась очень удобной для передачи в качестве аргумента в различные вспомогательные функции, например:
bool isCheck (Combo combo); // Проверка позиции на шах
bool isCheckmate (Combo combo); // на мат
bool isCheckByBishop (Combo combo); // есть ли шах от слона
Однако для записи результата базы решений этой структуры не достаточно, ещё нам потребуется…
Белый ящик
Целью нашей программы будет создание «белого ящика», в который будут складываться все позиции, в которых «ход белых», и для которых известно — какой именно ход нужно делать, и через сколько ходов будет гарантированно поставлен мат.
Составной частью «белого ящика» является следующая структура:
struct WhitesMove
{
public Combo combo;
public byte moves; // сколько ходов до мата
public Coord moveFrom; // правильный ход - откуда
public Coord moveTo; // куда
}
Для организации «белого ящика» проще всего открыть четырёхмерную матрицу. Каждая размерность этой матрицы соответствует возможной позиции каждой фигуры:
WhitesMove [ , , , ] box = new WhitesMove [64, 32, 64, 64];
первая размерность — координата белого короля.
вторая размерность — координата белого слона / 2.
третья размерность — координата белого коня.
четвёртая размерность — координата чёрного короля.
Главное — не перепутать их порядок :) Массив получится на 33% разряженным, но уж очень удобным для обработки. Именно в этом массиве будет храниться 8,388,608 записей для решения комбинаций.
Кстати, прежде чем начать писать все алгоритмы перебора, я создал пустой проект и проинициализировал эту четырёхмерную матрицу, дабы убедиться, что памяти хватит и не надо будет что-то дополнительное изобретать. Видимо, сказался опыт участия в олимпиадах по информатике прошлого тысячелетия, где размер структуры не мог превышать 64 килобайт, ибо Turbo Pascal 7.0.
Идея алгоритма
Кратко опишу основную идею решения этой задачи. В основу взят алгоритм поиска вширь, который пришлось немного доработать, так как в шахматы играют двое и ходы делаются по очереди. Поэтому вместо одной очереди нам потребуется две — «чёрная» и «белая».
Queue<BlacksMove> blackQueue = new Queue<BlacksMove>();
Queue<WhitesMove> whiteQueue = new Queue<WhitesMove>();
Со структурой WhitesMove мы уже познакомились. Структура BlacksMove немного проще, так как в ней нет надобности хранить последний ход чёрных.
struct BlacksMove
{
public Combo combo;
public byte moves;
}
Сначала в «чёрную очередь» мы разместим все матовые позиции, в которых ход чёрных. Потом из каждой такой позиции будем делать обратный ход за белых и формировать «белую очередь» — список позиций, в которых ход белых.
Эти действия нужно будет повторять до полного исчерпания всех возможных комбинаций.
Основной алгоритм в виде псевдокода:
Очищаем "белую очередь", "чёрную очередь", "белый ящик"
Ищем все матовые позиции
Добавляем их в "чёрную очередь"
Повторять
{
Пока "чёрная очередь" не пуста
Берём позицию из "чёрной очереди"
Перебираем для неё все обратные ходы белых
Если нет шаха чёрному королю
Если такой позиции нет в "белом ящике"
Добавляем позицию в "белый ящик"
Добавляем позицию в "белую очередь"
Пока "белая очередь" не пуста
Берём позицию из "белой очереди"
Перебираем для неё все возможные обратные ходы чёрного короля
Если из этой позиции любой ход ведёт
к известной позиции из "белого ящика"
Добавляем позицию в "чёрную очередь"
} Пока "чёрная очередь" не пустая
В "белом ящике" находится база решений
Матовые позиции
Создание базы правильных ходов начинается с поиска всех матовых комбинаций. Использование енумераторов ��озволило достаточно эффектно описать этот процесс.
foreach (Combo combo in AllCheckmates())
{
BlacksMove checkmate = new BlacksMove { combo = combo, moves = 0 };
blackQueue.Enqueue(checkmate);
}
Всего найдено 232 матовые позиции. Напомню, что мы ограничились только белопольным слоном.
Некоторые из них достаточно экзотические, не существующие и «кооперативные», это когда чёрный король сам полез под мат.

Шахматистам хорошо известно, что мат конём и белопольным слоном нужно ставить в белом углу. В чёрном углу мат возможен только если чёрные будут подыгрывать. Я специально разместил фото с именно таким псевдоматом в начале статьи, чтобы спровоцировать внимание настоящих шахматистов :)
Мат в один ход
Следующий этап — сделать обратный ход белых. То есть, для каждой найденной матовой позиции сделать все возможные обратные ходы белых.
Как сделать обратный ход? Учитывая, что взятия в наших позициях не предусмотрены, алгоритм достаточно простой — сделать любой ход белых, после которого не будет шаха чёрному королю.
Все найденные таким образом позиции можно уже складывать в «белый ящик», указывая, что до мата один ход, и какой именно ход для этого нужно сделать. Попутно помещаем найденные комбинации в «чёрную очередь».
Вот как выглядит эта часть алгоритма:
// Пока "чёрная очередь" не пуста
while (blackQueue.Count > 0)
{
// Берём позицию из "чёрной очереди"
BlacksMove black = blackQueue.Dequeue();
// Перебираем для неё все обратные ходы белых
foreach (WhitesMove white in AllWhiteBackMoves(black))
// Если нет шаха чёрному королю
if (!isCheck(white.combo))
// Если такой позиции нет в "белом ящике"
if (!whiteBox.Exists(white.combo))
{
// Добавляем позицию в "белый ящик"
whiteBox.Put (white);
// Добавляем позицию в "белую очередь"
whiteQueue.Enqueue(white);
}
}
Кстати, про yield
Использование енумераторов с yield-механизмом позволяет очень красиво реализовать различные переборы, например, так выглядит функция перебора всех возможных ходов белыми фигурами:
IEnumerable<WhitesMove> AllWhiteBackMoves(BlacksMove black)
{
foreach (WhitesMove white in AllWhiteKingMoves(black))
yield return white;
foreach (WhitesMove white in AllWhiteBishopMoves(black))
yield return white;
foreach (WhitesMove white in AllWhiteKnightMoves(black))
yield return white;
}
Всего было найдено 920 таких позиций, вот самые интересные:
Ход конём:



Ход слоном:


Ход королём:

Мат в полтора хода
Следующий этап — сделать обратный ход чёрных. С этим алгоритмом я провозился дольше всего, было сделано немало ошибок, прежде чем всё заработало верно.
На первый взгляд, всё аналогично предыдущему варианту: для каждой позиции из «белой очереди» необходимо перебрать все возможные ходы чёрного короля. И добавлять все найденные комбинации в «чёрную очередь» — ведь это мат в полтора хода, от которого можно будет потом снова делать обратный ход за белых — будет мат в два хода — и так продолжать, пока не будут пересмотрены все варианты.
В этом и была ошибка. При любом возможном ходе чёрных получается «кооперативный» мат в полтора хода, а на самом деле король не обязательно будет идти под мат. Указал мне на эту ошибку Дмитрий Гринь, который посещал все мои вебинары по созданию этой программы, за что ему отдельное спасибо.
Правильный алгоритм следующий: для каждой позиции N после обратного хода чёрного короля нужно перебрать все возможные его прямые ходы, чтобы убедиться, что все они ведут к знакомым позициям из «белого ящика», то есть ведут к мату. И только после этого позицию N можно добавлять в «чёрную очередь». А если из позиции N чёрный король может «улизнуть», то такой вариант пропускаем. Она встретится на последующих итерациях, когда знакомых позиций будет больше.
Вот как выглядит эта часть алгоритма:
// Пока "белая очередь" не пуста
while (whiteQueue.Count > 0)
{
// Берём позицию N из "белой очереди"
WhitesMove white = whiteQueue.Dequeue();
Combo whiteFigures = white.combo;
// Перебираем для N все возможные обратные ходы чёрного короля
foreach (BlacksMove black in AllBlackBackMoves(white))
{
bool solved = true;
// Перебираем все возможные ходы чёрного короля
foreach (Coord blackKing in AllKingMoves(black.combo.blackKing))
{
whiteFigures.blackKing = blackKing; // переставляем чёрного короля
if (isCheck(whiteFigures)) // под шах не ходим
continue;
if (box.Exists(whiteFigures)) // решённые позиции пропускаем
continue;
solved = false; // чёрный король смог "улизнуть"
break;
}
// Если из этой позиции любой ход ведёт
// к известной позиции из "белого ящика"
if (solved)
// Добавляем позицию в "чёрную очередь"
blackQueue.Enqueue(black);
}
}
Всего было найдено 156 комбинаций «Мат в полтора хода».
Итеративность полуходов
Описанные алгоритмы создания полуходов необходимо зациклить. Из «чёрной очереди» мы формируем «белую очередь», а потом наоборот — из «белой» формируем «чёрную». И так до тех пор, пока не будут исчерпаны все новые позиции. «Белая коробка» заполняется на этапе формирования «белой очереди», так как в неё помещаются позиции, в которых ход белых.
Готовый алгоритм перебора всех вариантов отработал где-то за 12 минут и остановился на 33 ходу. Именно столько максимум ходов нужно, чтобы заматовать чёрного короля конём и слоном из любой позиции.
Кстати, таких «самых сложных» позиций оказалось не так много, всего 156, вот одна из них:

Мата не будет!
Есть немало позиций, в которых даже после хода белых чёрный король может съесть коня или слона и выйти на ничью. Также есть патовые варианты. Вот несколько самых интересных позиций.




Как хранить базу решений
Каким способом хранить найденную базу решений?
Самый простой и неправильный способ — использовать сериализацию. Засериализованный четырёхмерный массив структуры занял 1.7 гигабайта(!) на диске. Процесс сериализации длился минут шесть, на десериализацию потребовалось примерно столько же.
Такой вариант, ясное дело, не подходит. К тому же, на практике нет надобности использовать весь четырёхмерный массив. Для конкретной позиции нужна только одна запись.
Эврика! Для экономии места ещё можно избавиться от хранения координат фигур для каждой комбинации. Когда у нас есть четырёхмерный массив, то позиция каждой фигуры на доске однозначно определяется её индексом в массиве.
Было решено хранить всю базу решений в одном файле — как линейную развёртку четырёхмерного массива. Для любой возможной позиции вычисляется адрес, по которому записан правильный ответ.
Как максимально компактно записать нужный нам ответ? Позицию фигур хранить не надо, поэтому остаётся только три числа — сколько ходов до мата, чем ходить и куда ходить. Именно так однозначно определяется правильный ход за белых.
6 бит. Сколько ходов до мата — это целое число от 0 до 33.
2 бита. Какая фигура ходит — три возможных варианта, король, слон или конь.
6 бит. Куда фигура ходит — индекс поля на доске от 0 до 63.
Значит, на каждую запись решения достаточно два байта:
1 байт — сколько ходов до мата, или 0, если позиция незнакомая.
2 байт — FFNNNNNN
FF — номер фигуры, которой нужно ходить (1 — король, 2 — слон, 3 — конь)
NNNNNN — координата клетки — куда ходить (от 0 до 63).
Итак, файл базы решений занимает 64 * 32 * 64 * 64 слов = ровно 16 мегабайт. Размещение фигур задаётся координатами каждого слова, в первом байте — количество ходов до мата (или 0 если решения нет), во втором байте хранится правильный ход.
Можно было бы ещё в два раза уменьшить размер файла, если не хранить количество ходов до мата, но так играть будет не интересно.
Координаты чёрнопольного белого слона
Пришло время платить за оптимизацию. Нужно реализовать алгоритм пересчёта координат для комбинаций с «чёрно-белым» слоном.
Это было сделано следующим образом. Если координата слона попадает на чёрное поле, то необходимо координаты всех фигур на доске «перевернуть». При этом координата Y остаётся неизменной, а X меняется на 7-X. Наглядная демонстрация переворота координат см. на рисунке.

Если слон стоит на белой клетке, то сначала необходимо «перевернуть» координаты всех фигур. Потом искать позицию в ба��е решений. И ещё раз «перевернуть» считанную оттуда координату правильного хода.
Визуализация базы решений
Итак, Задача решена!
База решений создана.
Но как её продемонстрировать?
Самый наглядный способ — использовать web-технологии, чтобы можно было просто дать ссылку на работающий пример. На моей «формуле программиста» уже был создан фотокурс "Нано-шахматы", где с использованием технологий HTML, CSS, JavaScript и PHP была создана интерактивная шахматная доска для игры вдвоём без правил. Именно этот скрипт был взят за основу.
Я оставил только четыре фигуры, убрал возможность взятия, добавил РНР-функции для считывания правильных ходов из базы решений и «вдохнул жизнь» через JavaScript.
На странице www.videosharp.info/chess вы можете поэкспериментировать с базой решений.

Для каждой позиции рассчитываются ходы как за белых, так и за чёрных.
За белых — лучший ход, который ведёт к мату.
За чёрных — сколько ходов до мата на любой возможный ход.
Мышкой можно делать любые перемещения фигур, не обязательно по правилам.
Скрипт рассчитает вариант для любой позиции, либо напишет, что вариантов нет.
Интересно поиграть, выполняя предложенные ходы или передвигая фигуры на своё усмотрение.
Заключение
Была проделана большая, интересная работа по решению шахматной задачи.
Если вы желаете повторить этот путь — можете посмотреть видеозаписи по созданию этой программы с нуля до результата с подробными пояснениями и самостоятельными заданиями.
Желаю удачи!