Очень надеялся опубликоваться с настроением «Россия — в полуфинале», но немного не хватило. Хотя для меня всегда характер был выше результата, и характер я видел. Спасибо парням. Продолжаем совершенствоваться в том, что умеем. Они — в футболе, мы — в проектировании печатных плат. Поехали, шестая часть. В ней рассматривается влияние потерь в линии на длительность фронта сигнала, приводится модель перекрёстных помех и даются рекомендации по их снижению.
В предыдущей статье было показано, что несогласованность линии приводит к появлению отражений и искажению сигнала. Все методы согласования предполагают обеспечение равенства импедансов нагрузки и/или источника волновому сопротивлению сигнальной линии. Отсюда следует вывод, что если импеданс нагрузки непостоянен и зависит от некоторого параметра, точное согласование обеспечить невозможно. Например, входной каскад логических элементов всегда характеризуется эквивалентной входной ёмкостью (обычно это единицы пикофарад). Напряжение на входном конденсаторе V при переходных процессах, а следовательно, и его импеданс

зависят от времени. Возникающие при этом отражения выражаются в замедлении длительности фронта на время τ ≈ 2,2∙Z0C (по аналогии с RC-цепью). Если длительность фронта источника tR мала по сравнению с τ, то именно процесс зарядки конденсатора будет определять длительность фронта на дальнем конце линии.
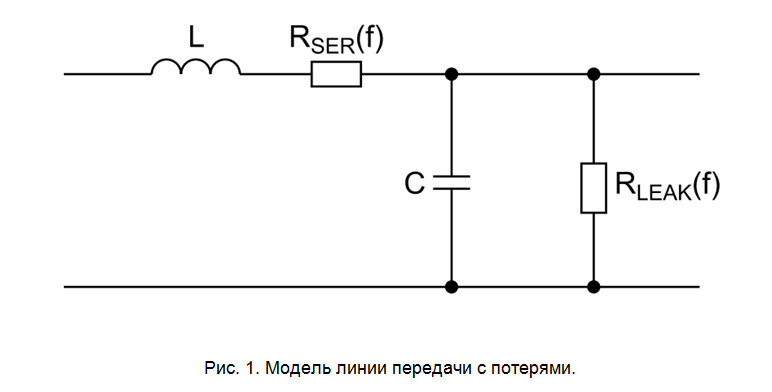
В реальной сигнальной линии фронт сигнала замедляется не только с увеличением на ней емкостной нагрузки, но и по причине потерь, причинами которых являются омические потери и потери утечки в диэлектрике. На рис. 1 изображена модель линии с потерями, где последовательное сопротивление

моделирует омические потери (в т.ч. скин-эффект), а сопротивление

диэлектрические (здесь tg(δ) – тангенс угла потерь, характеристика материала диэлектрика). Увеличение потерь с ростом частоты приводит к тому, что высокочастотные составляющие сигнала ослабляются значительнее, что и приводит к замедлению фронта сигнала. Эрик Богатин в [1] приводит формулу для оценки длительности фронта на выходе сигнальной линии с потерями длиной L и диэлектриком с проницаемостью ε и тангенсом угла потерь tg(δ):
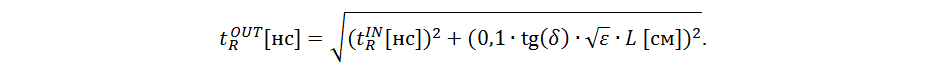
Далее, из условия ∆tR=tROUT-tRIN<0,1∙tRIN можно вывести оценочный критерий необходимости учёта эффектов, связанных с потерями в сигнальной линии.
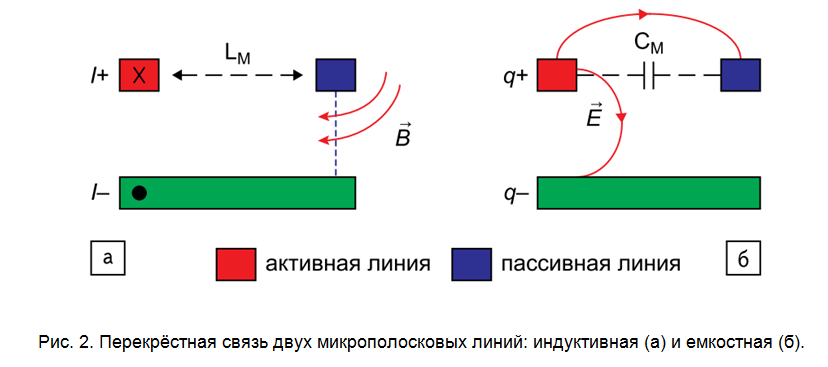
Другим источником потерь является перекрёстная связь с соседними проводниками (англ. coupling), которая приводит к искажениям сигнала в активной линии (по причине потерь в ближнем поле) и к наведённым перекрёстным помехам (англ. crosstalk) в пассивной линии. Эффект возникает за счёт двух физических принципов – электрической (емкостной) связи и магнитной (индуктивной) связи. На рис. 2 показаны определяющие параметры перекрёстной связи – взаимная индуктивность LM и взаимная ёмкость СМ, зависящие прежде всего от геометрии и параметров материалов.
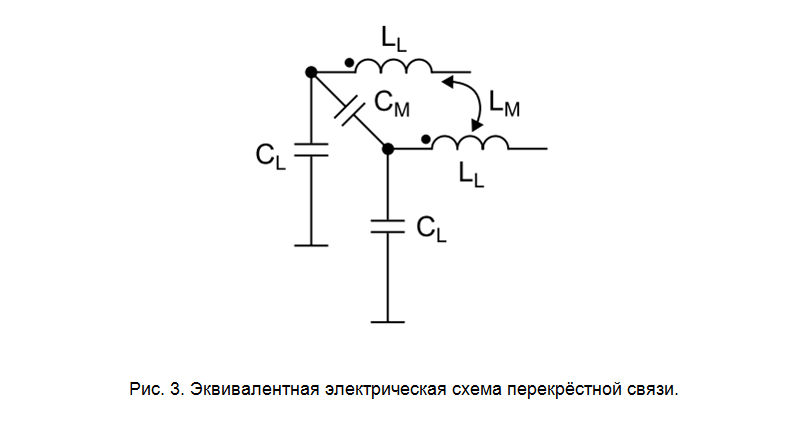
Приведённая на рис. 3 эквивалентная электрическая схема перекрёстной связи может использоваться при выполнении расчётов и моделирования. При этом количество N таких последовательных звеньев должно быть тем больше, чем выше электрическая длина линий TD и требуемая спектральная полоса модели BW:
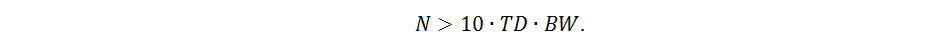
Емкость CL и индуктивность LL звеньев можно рассчитать по формулам:
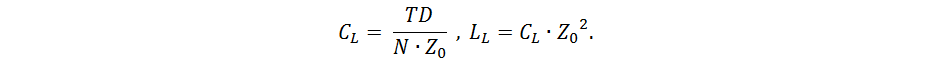
Основная трудность при моделировании эквивалентной схемы перекрёстной связи заключается в вычислении значений LM и СM в расчёте на одно звено. Для некоторых случаев существуют оценочные аналитические соотношения [2], в общем случае для решения этой задачи применяются специализированные программные средства на основе численных методов.
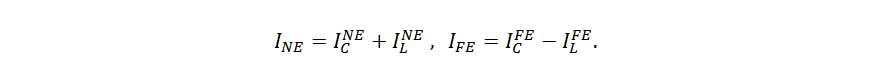
Эквивалентная схема электрически короткой (для временной задержки которой выполняется TD < 1/5∙tR пассивной линии представлена на рис. 5, где источники электрической энергии определяются формулами:
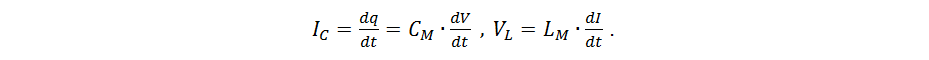

Схема является упрощённой и применима только для оценки амплитуды перекрёстных помех. Однако для данной схемы выводятся аналитические соотношения, которые показывают основные зависимости, выполняющиеся и для более сложных случаев:

Приведённая выше теория для простоты рассматривала пример двух проводников. Однако важно понимать, что для цифровых печатных плат типичной является ситуация, когда несколько сигнальных линий синхронно изменяют своё состояние. Так как перекрёстные помехи от нескольких активных линий складываются, то в таком случае величина помехи может стать критической, приводя к некорректному функционированию системы. Для численного моделирования в этом случае применяется специализированное программное обеспечение, но основополагающие принципы снижения величины перекрёстных помех остаются те же, что и приведённой выше рекомендации.
[1] Bogatin E. «Signal and power integrity — simplified», 2nd ed., Pearson, 2010
[2] «Mutual Inductance and Capacitance Algorithm», rev. 01.8.2
[3] Adamczyk B. «EMC Crosstalk between PCB Traces», West Michigan EMC Chapter Meeting, 2013
Статья была впервые опубликована в журнале «Компоненты и технологии» 2018, №4. Публикация на «Habr» согласована с редакцией журнала.
В предыдущей статье было показано, что несогласованность линии приводит к появлению отражений и искажению сигнала. Все методы согласования предполагают обеспечение равенства импедансов нагрузки и/или источника волновому сопротивлению сигнальной линии. Отсюда следует вывод, что если импеданс нагрузки непостоянен и зависит от некоторого параметра, точное согласование обеспечить невозможно. Например, входной каскад логических элементов всегда характеризуется эквивалентной входной ёмкостью (обычно это единицы пикофарад). Напряжение на входном конденсаторе V при переходных процессах, а следовательно, и его импеданс

зависят от времени. Возникающие при этом отражения выражаются в замедлении длительности фронта на время τ ≈ 2,2∙Z0C (по аналогии с RC-цепью). Если длительность фронта источника tR мала по сравнению с τ, то именно процесс зарядки конденсатора будет определять длительность фронта на дальнем конце линии.
В реальной сигнальной линии фронт сигнала замедляется не только с увеличением на ней емкостной нагрузки, но и по причине потерь, причинами которых являются омические потери и потери утечки в диэлектрике. На рис. 1 изображена модель линии с потерями, где последовательное сопротивление

моделирует омические потери (в т.ч. скин-эффект), а сопротивление

диэлектрические (здесь tg(δ) – тангенс угла потерь, характеристика материала диэлектрика). Увеличение потерь с ростом частоты приводит к тому, что высокочастотные составляющие сигнала ослабляются значительнее, что и приводит к замедлению фронта сигнала. Эрик Богатин в [1] приводит формулу для оценки длительности фронта на выходе сигнальной линии с потерями длиной L и диэлектриком с проницаемостью ε и тангенсом угла потерь tg(δ):
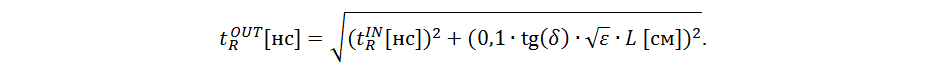

Далее, из условия ∆tR=tROUT-tRIN<0,1∙tRIN можно вывести оценочный критерий необходимости учёта эффектов, связанных с потерями в сигнальной линии.
Как видно из этой рекомендации, в большинстве приложений при разработке печатных плат можно использовать модель сигнальной линии без потерь, где RLEAK = ∞ и RSER = 0.Р.1.
Для сигнальной линии, длина L которой соответствует критерию L [см]< 5/(tg(δ)∙√ε)∙tR [нс], влияние потерь на длительность фронта сигнала можно не учитывать. Для диэлектрика FR4 это условие приобретает вид L [см]< 125∙tR [нс].
Другим источником потерь является перекрёстная связь с соседними проводниками (англ. coupling), которая приводит к искажениям сигнала в активной линии (по причине потерь в ближнем поле) и к наведённым перекрёстным помехам (англ. crosstalk) в пассивной линии. Эффект возникает за счёт двух физических принципов – электрической (емкостной) связи и магнитной (индуктивной) связи. На рис. 2 показаны определяющие параметры перекрёстной связи – взаимная индуктивность LM и взаимная ёмкость СМ, зависящие прежде всего от геометрии и параметров материалов.

Приведённая на рис. 3 эквивалентная электрическая схема перекрёстной связи может использоваться при выполнении расчётов и моделирования. При этом количество N таких последовательных звеньев должно быть тем больше, чем выше электрическая длина линий TD и требуемая спектральная полоса модели BW:
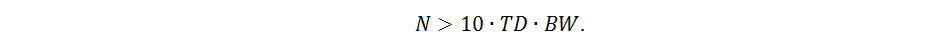
Емкость CL и индуктивность LL звеньев можно рассчитать по формулам:
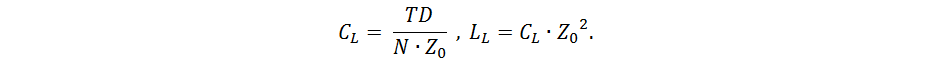

Основная трудность при моделировании эквивалентной схемы перекрёстной связи заключается в вычислении значений LM и СM в расчёте на одно звено. Для некоторых случаев существуют оценочные аналитические соотношения [2], в общем случае для решения этой задачи применяются специализированные программные средства на основе численных методов.
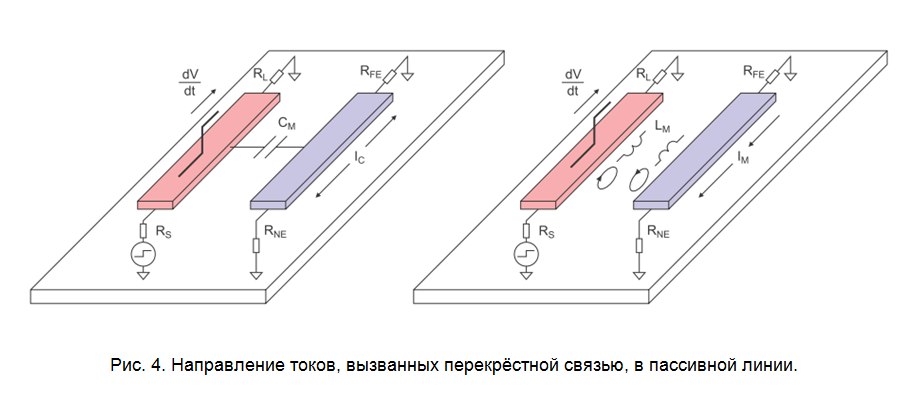
Электрическая и магнитная связь приводят к потерям энергии и искажению сигнала в активной линии и появлению сигнала в пассивной линии. Токи емкостной IC и индуктивной IM связи (рис. 4) однонаправлены в сторону источника (англ. near-end) и противоположно направлены в сторону нагрузки (англ. far-end):Р.2.
Величины взаимной индуктивности и взаимной ёмкости уменьшаются с увеличением расстояния между проводниками и с уменьшением расстояния между проводником и опорным слоем. Кроме этого, наличие вырезов в опорном слое приводит к значительному увеличению взаимной индуктивности.
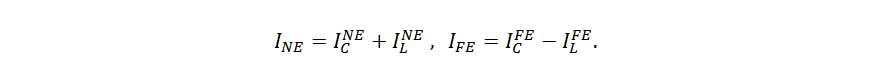

Эквивалентная схема электрически короткой (для временной задержки которой выполняется TD < 1/5∙tR пассивной линии представлена на рис. 5, где источники электрической энергии определяются формулами:
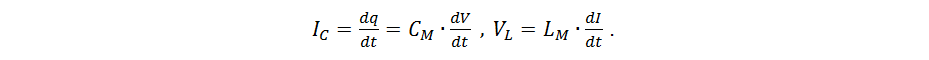

Схема является упрощённой и применима только для оценки амплитуды перекрёстных помех. Однако для данной схемы выводятся аналитические соотношения, которые показывают основные зависимости, выполняющиеся и для более сложных случаев:

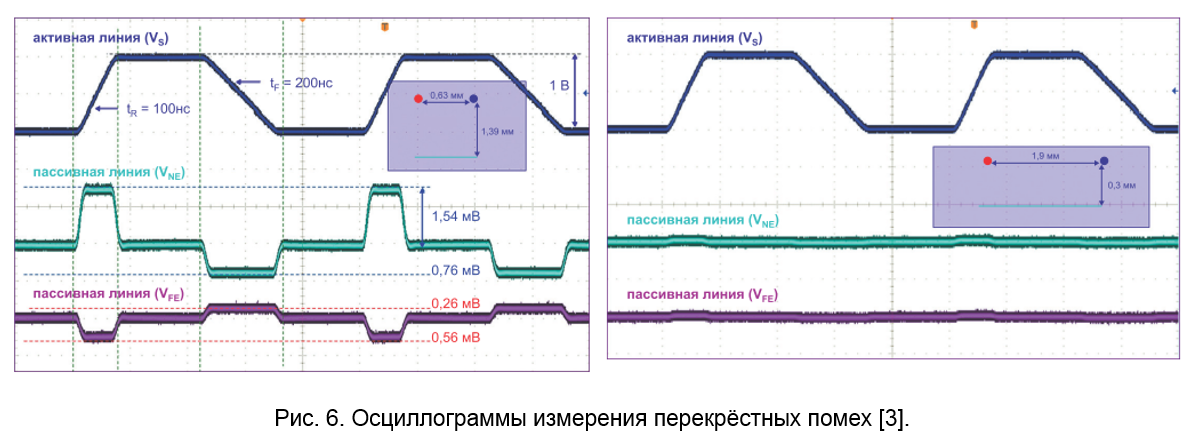
На рис. 6 изображены осциллограммы измерения перекрёстных помех между двумя 50-омными микрополосковыми линиями на экспериментальной плате в двух случаях: w ~ 2,5 мм, s ~ 0,6 мм, h = 1,39 мм и w ~ 0,6 мм, s ~ 1,9 мм, h = 0,3 мм. Длина параллельных участков дорожек составляет порядка 30 см. Стоит обратить внимание на то, что и длительность фронтов сигнала на активной линии значительно превышает типичные значения для быстродействующих цифровых печатных плат. Величина помех на рис. 5 не должна рассматриваться как характерная, данные осциллограммы прежде всего являются наглядным представлением влияния на величину помехи длительности фронта сигнала, расстояния между проводниками и близости опорного слоя.Р.3.
Методы снижения перекрёстных помех:
- Увеличение длительности фронтов сигнала в активной линии (англ. aggressor, active line).
- Снижение параллельного участка линий.
- Увеличение расстояния между проводниками. Существуют рекомендации минимального расстояния между краями печатных дорожек s ~ 6 ∙h или s ~ 3 ∙w, где h – расстояние до опорного слоя, w – ширина дорожки.
- Снижение расстояния между проводником и опорным слоем.
- Подбор сопротивлений на концах активной и пассивной (англ. victim, quiet line) линий.
- Применение экранирующих проводников (англ. guard trace), закороченных на опорный слой на концах и, по возможности, вдоль длины (порядка трёх переходных отверстий на длину tR∙v).
- Применение встроенных микрополосковых (англ. embedded microstrip) или полосковых линий, для которых в силу симметрии диэлектрика выполняется VFE ≈ 0.

Приведённая выше теория для простоты рассматривала пример двух проводников. Однако важно понимать, что для цифровых печатных плат типичной является ситуация, когда несколько сигнальных линий синхронно изменяют своё состояние. Так как перекрёстные помехи от нескольких активных линий складываются, то в таком случае величина помехи может стать критической, приводя к некорректному функционированию системы. Для численного моделирования в этом случае применяется специализированное программное обеспечение, но основополагающие принципы снижения величины перекрёстных помех остаются те же, что и приведённой выше рекомендации.
Литература.
[1] Bogatin E. «Signal and power integrity — simplified», 2nd ed., Pearson, 2010
[2] «Mutual Inductance and Capacitance Algorithm», rev. 01.8.2
[3] Adamczyk B. «EMC Crosstalk between PCB Traces», West Michigan EMC Chapter Meeting, 2013
Статья была впервые опубликована в журнале «Компоненты и технологии» 2018, №4. Публикация на «Habr» согласована с редакцией журнала.