В чем рисовать векторные картинки? Для меня, как и для многих других, ответ довольно очевиден: скорее всего, в иллюстраторе. Ну или в инкскейпе. Так же я думал, когда мне заказали отрисовать штук восемьсот картинок для учебника физики. Ничего такого, просто черно-белые технические иллюстрации со всякими блоками, шарами, пружинами, линзами, машинками, тракторами и прочим подобным. Предполагалось, что верстаться книга будет в латехе, а мне были предоставлены вордовские файлы со вставленными картинками — то карандашными набросками, то сканами из других книг — и вроде бы рукопись в каком-то виде. В этом случае первая мысль — рисовать в инкскейпе — уступила фантазиям на тему «как бы это так все автоматизировать». Лучшим вариантом показался в тот момент почему-то MetaPost.
Самый весомый плюс подобного решения — каждая картинка может быть небольшой функцией от нескольких переменных; такую картинку легко, например, менять в размере и подгонять под конкретные заранее неизвестные обстоятельства полосы без нарушения важных пропорций, чего трудновато добиться более традиционными средствами. А еще повторяющиеся элементы — те самые шары и пружины — можно заставить вести себя гораздо интереснее, чем позволяют средства «человеческих» векторных редакторов.
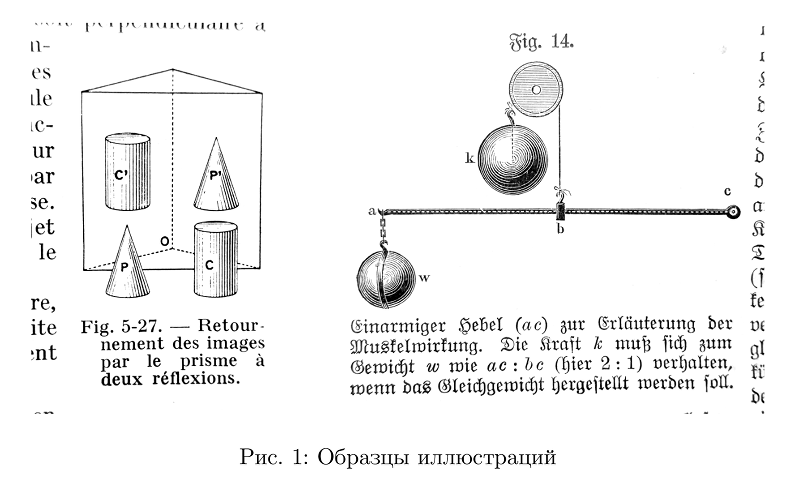
Картинки мне хотелось сделать со штриховкой, наподобие такой, какая встречается в старых книжках.
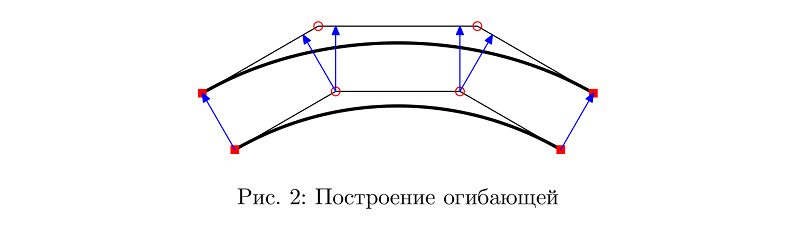
Для начала надо было получить линии переменной толщины. Основная сложность тут — построить кривую, более или менее параллельную данной и нужным образом меняющую расстояние до данной. Я опирался на самый, наверное, примитивный способ, по которому отрезки, соединяющие промежуточные точки кривой Безье, просто параллельно переносятся на данное расстояние. С тем отличием, что это расстояние может меняться вдоль кривой.
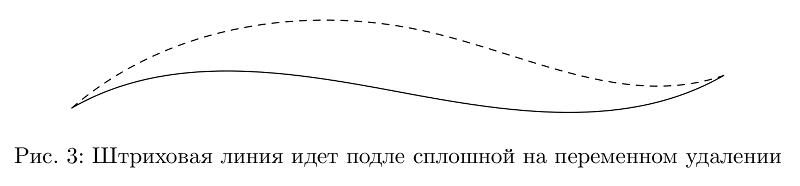
В большинстве случаев это позволяет добиться сносного результата.
Теперь из двух таких кривых можно сделать контур линии переменной толщины.

Толщина должна быть чем-то ограничена снизу, иначе слишком тонкие части линий при печати возьмет на себя растр, а это обычно не очень красиво. Один из вариантов — делать все линии, толщина которых меньше какого-то значения, штриховыми линиями этой же минимальной толщины, такими, чтобы общее количество краски на единицу длины в среднем соответствовало таковому для линии целевой толщины. То есть вместо того, чтобы уменьшать количество краски с боков линии, начинать выгрызать ее поперечными полосами.

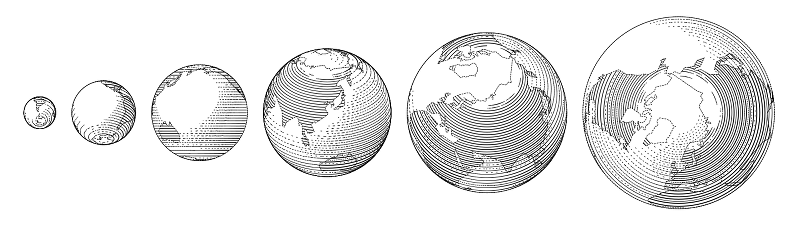
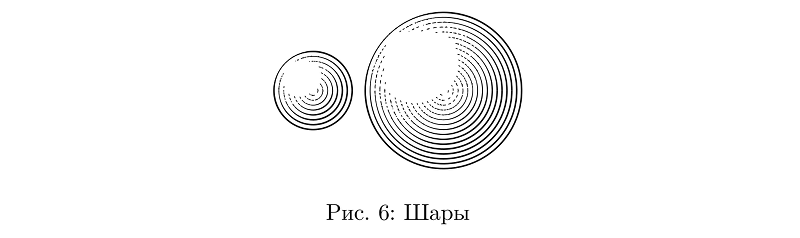
Теперь можно рисовать шары. Это могут быть просто концентрические круги, толщины линий у которых определяются функцией от освещенности шара в точках, через которые линии проходят.
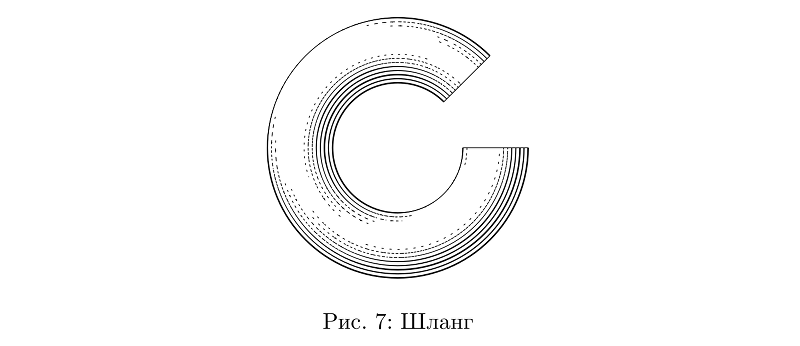
Другой удобный примитив — «шланги»: грубо говоря, цилиндры, которые можно по всякому гнуть. Пока они постоянного сечения, с ними всё просто.
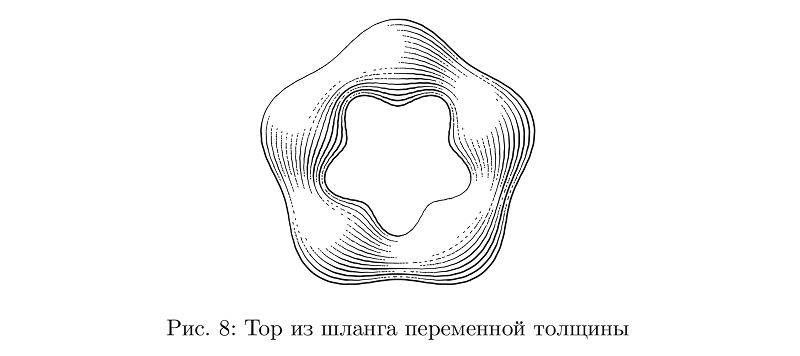
Если же толщина меняется, то надо сообразно менять и количество штрихов, сохраняя при этом среднюю плотность заливки неизменной, а также учитывать изменения толщины при расчете освещенности.
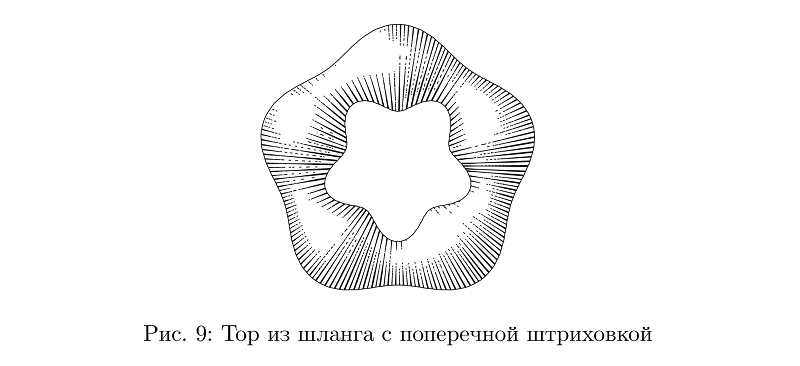
Eще есть шланги с поперечной штриховкой, но для них решить задачу сохранения средней плотности заливки оказалось сложнее, так что во многих случаях они пока выглядят не очень.
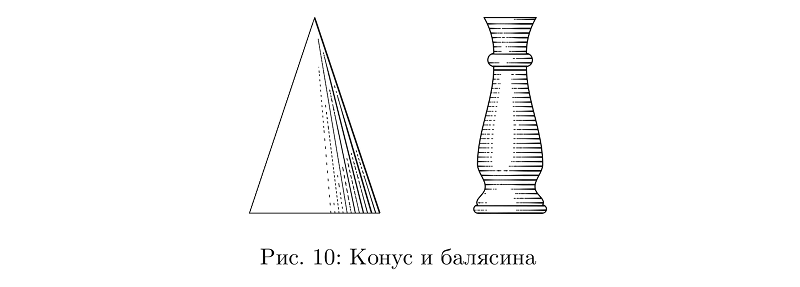
В принципе, из одних только шлангов можно сделать кучу всего: от конусов и цилиндров до балясин.
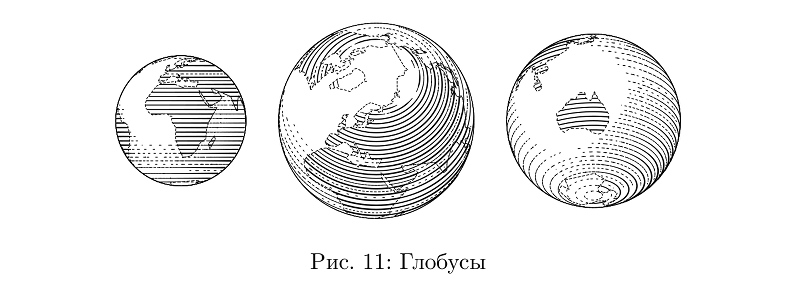
Кое-что из того, что можно соорудить из таких деталей, есть в библиотеке. Скажем, глобус — это в основе своей шар.
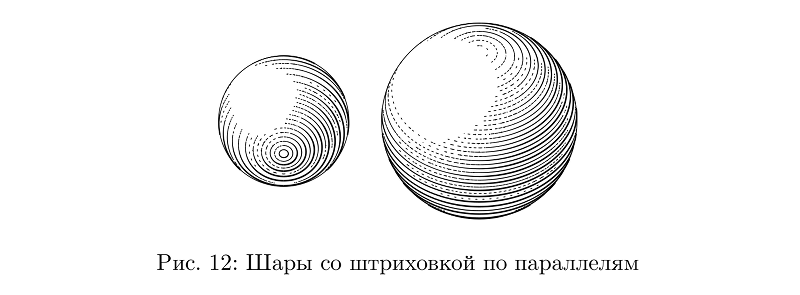
Хотя нет: тут штриховка идет по параллелям, и управлять толщиной штриха для сохранения плотности заливки еще сложнее, чем в случае поперечной штриховки на шлангах, так что это отдельный тип шара.
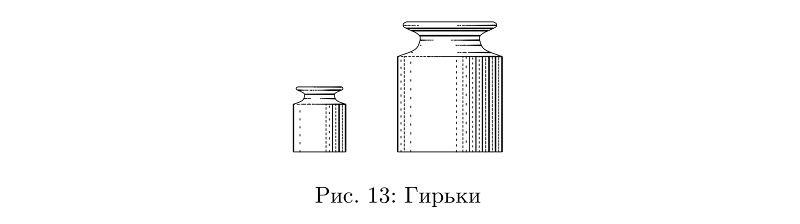
А гирька — это незамысловатая конструкция из двух видов шлангов переменной толщины.
Еще есть инструмент, чтобы завязывать шланги в узлы.
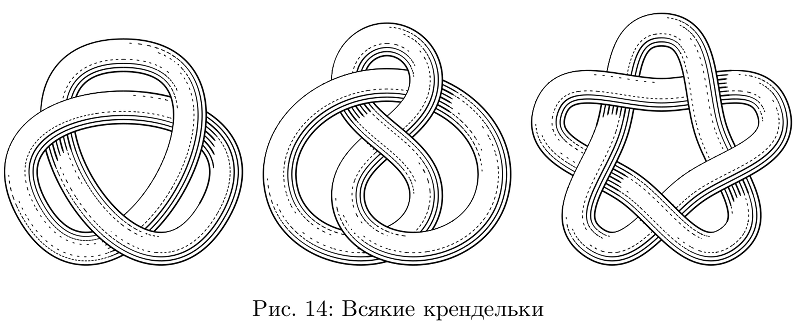
Тени у узлов — некоторое усложнение в модели освещения. В принципе, никто не мешает пользоваться ими и в других случаях, но цели уходить глубоко в объем я себе не ставил, так что пока это и не очень удобно, и не везде работает.
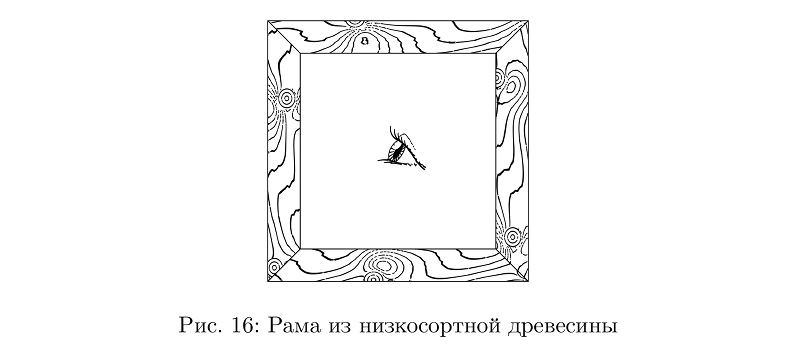
А, еще, конечно, нужна текстура дерева. Влияние характера роста сучков на рисунок срезов годичных колец — тема для серьезного исследования. Очень упрощая, можно представить себе годичные кольца параллельными плоскостями, в которые вносят искажения сучки. Так достаточно описать изменение плоскости какой-нибудь не очень мудреной функцией (функцией сучка) и считать серию изолиний для суммы набора таких функций искомым рисунком годичных колец.
Глаз из картинки выше может немного то открываться, то прищуриваться, и ширина зрачка у него меняется. Смысла особого в этом нет, но так получается более живенько, чем если бы такие мелочи везде были механически одинаковыми.

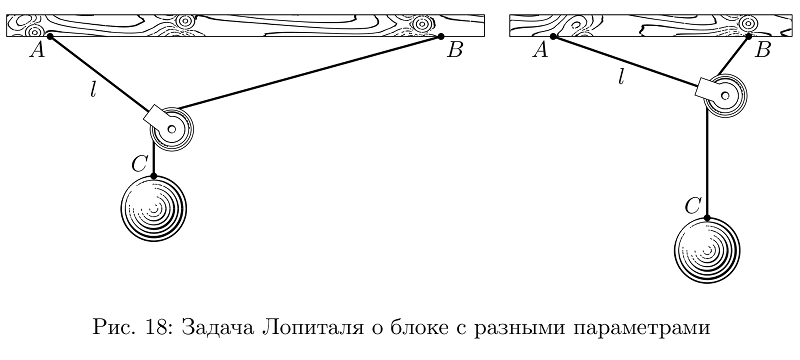
Чаще всего картинки были не очень сложные, но если подходить к делу со всей серьезностью, то многие задачи нужно решить, чтобы осмысленно их проиллюстрировать. Вот, скажем, задача Лопиталя о блоке (не знаю, как ее правильно по-русски называют, в учебнике ее не было, здесь просто для примера): висит на веревке длины l, подвешенной в точке A, блок, он зацеплен за другую веревку, подвешенную на той же высоте в точке B, на второй веревке висит груз C. Спрашивается, если веревки и блок невесомы, где окажется груз? На удивление, и решение задачи, и построение не такие уж и элементарные, но зато, играя несколькими переменными, можно легко сделать картинку именно такой, какая будет лучше всего смотреться на полосе, оставаясь при этом правдивой.
А что учебник? Увы и ах, когда уже были готовы почти все иллюстрации и верстка, что-то там случилось и он так и не вышел. Поэтому, наверное, некоторое время спустя я и переписал все основные штуки из получившейся библиотеки заново и выложил код на гитхаб. Какие-то кунштюки туда не вошли: к примеру, электрические схемы или функция для рисования машинок и тракторов. Какие-то — добавились: узлы, например.
Работает вся эта кухня небыстро: на то, чтобы собрать все картинки к этой статье с LuaLaTeX на моем ноутбуке с i5-4200U 1.6 ГГц, уходит примерно минута. Для очень многих вещей используется генератор псевдослучайных чисел, поэтому аналогичные картинки будут выглядеть немного по-разному не только внутри одного прогона (это фича), но и каждый следующий прогон даст картинки, отличные от предыдущего. Но всегда можно выставить в преамбуле

Самый весомый плюс подобного решения — каждая картинка может быть небольшой функцией от нескольких переменных; такую картинку легко, например, менять в размере и подгонять под конкретные заранее неизвестные обстоятельства полосы без нарушения важных пропорций, чего трудновато добиться более традиционными средствами. А еще повторяющиеся элементы — те самые шары и пружины — можно заставить вести себя гораздо интереснее, чем позволяют средства «человеческих» векторных редакторов.
Картинки мне хотелось сделать со штриховкой, наподобие такой, какая встречается в старых книжках.

Для начала надо было получить линии переменной толщины. Основная сложность тут — построить кривую, более или менее параллельную данной и нужным образом меняющую расстояние до данной. Я опирался на самый, наверное, примитивный способ, по которому отрезки, соединяющие промежуточные точки кривой Безье, просто параллельно переносятся на данное расстояние. С тем отличием, что это расстояние может меняться вдоль кривой.

В большинстве случаев это позволяет добиться сносного результата.

Код примера
Здесь и далее предполагается, что библиотека скачана и где-то есть строка
или в LuaLaTeX:
input fiziko.mp;. Быстрее всего запустить и посмотреть в ConTeXt (тогда beginfig и endfig не нужны):\starttext
\startMPcode
input fiziko.mp;
тут код
\stopMPcode
\stoptext
или в LuaLaTeX:
\documentclass{article}
\usepackage{luamplib}
\begin{document}
\begin{mplibcode}
input fiziko.mp;
тут код
\end{mplibcode}
\end{document}
beginfig(3);
path p, q; % синтаксис у метапоста, как мне кажется, довольно понятный, так что комментарии буду оставлять в основном к своим штукам
p := (0,-1/4cm){dir(30)}..(5cm, 0)..{dir(30)}(10cm, 1/4cm);
q := offsetPath(p)(1cm*sin(offsetPathLength*pi)); % первый аргумент тут — сам путь, а второй — функция от расстояния вдоль пути (offsetPathLength, меняется от 0 до 1), определяющая, на каком удалении будет проходить огибающая
draw p;
draw q dashed evenly;
endfig;
Теперь из двух таких кривых можно сделать контур линии переменной толщины.

Код примера
beginfig(4);
path p, q[];
p := (0,-1/4cm){dir(30)}..(5cm, 0)..{dir(30)}(10cm, 1/4cm);
q1 := offsetPath(p)(1/2pt*(sin(offsetPathLength*pi)**2)); % огибающая по одну сторону пути
q2 := offsetPath(p)(-1/2pt*(sin(offsetPathLength*pi)**2)); % и по другую
fill q1--reverse(q2)--cycle;
endfig;
Толщина должна быть чем-то ограничена снизу, иначе слишком тонкие части линий при печати возьмет на себя растр, а это обычно не очень красиво. Один из вариантов — делать все линии, толщина которых меньше какого-то значения, штриховыми линиями этой же минимальной толщины, такими, чтобы общее количество краски на единицу длины в среднем соответствовало таковому для линии целевой толщины. То есть вместо того, чтобы уменьшать количество краски с боков линии, начинать выгрызать ее поперечными полосами.

Код примера
beginfig(5);
path p;
p := (0,-1/4cm){dir(30)}..(5cm, 0)..{dir(30)}(10cm, 1/4cm);
draw brush(p)(1pt*(sin(offsetPathLength*pi)**2)); % те же аргументы, что и у огибающей, но для толщины кисти
endfig;
Теперь можно рисовать шары. Это могут быть просто концентрические круги, толщины линий у которых определяются функцией от освещенности шара в точках, через которые линии проходят.

Код примера
beginfig(6);
draw sphere.c(1.2cm);
draw sphere.c(2.4cm) shifted (2cm, 0);
endfig;
Другой удобный примитив — «шланги»: грубо говоря, цилиндры, которые можно по всякому гнуть. Пока они постоянного сечения, с ними всё просто.

Код примера
beginfig(7);
path p;
p := subpath (1,8) of fullcircle scaled 3cm;
draw tube.l(p)(1/2cm); % аргументы — путь и функция ширины шланга, которая здесь постоянна
endfig;
Если же толщина меняется, то надо сообразно менять и количество штрихов, сохраняя при этом среднюю плотность заливки неизменной, а также учитывать изменения толщины при расчете освещенности.

Код примера
beginfig(8);
path p;
p := pathSubdivide(fullcircle, 2) scaled 3cm;
draw tube.l(p)(1/2cm + 1/6cm*sin(offsetPathLength*10pi));
endfig;
Eще есть шланги с поперечной штриховкой, но для них решить задачу сохранения средней плотности заливки оказалось сложнее, так что во многих случаях они пока выглядят не очень.

Код примера
beginfig(9);
path p;
p := pathSubdivide(fullcircle, 2) scaled 3cm;
draw tube.t(p)(1/2cm + 1/6cm*sin(offsetPathLength*10pi));
endfig;
В принципе, из одних только шлангов можно сделать кучу всего: от конусов и цилиндров до балясин.

Код примера
beginfig(10);
draw tube.l ((0, 0) -- (0, 3cm))((1-offsetPathLength)*1cm) shifted (-3cm, 0); % очень простой конус
path p;
p := (-1/2cm, 0) {dir(175)} .. {dir(5)} (-1/2cm, 1/8cm) {dir(120)} .. (-2/5cm, 1/3cm) .. (-1/2cm, 3/4cm) {dir(90)} .. {dir(90)}(-1/4cm, 9/4cm){dir(175)} .. {dir(5)}(-1/4cm, 9/4cm + 1/5cm){dir(90)} .. (-2/5cm, 3cm); % огибающая балясины
p := pathSubdivide(p, 6);
draw p -- reverse(p xscaled -1) -- cycle;
tubeGenerateAlt(p, p xscaled -1, p rotated -90); % более низкоуровневая штука, чем tube.t, первые два аргумента — два пути — стороны шланга, третий — кривая огибающей.
endfig;
Кое-что из того, что можно соорудить из таких деталей, есть в библиотеке. Скажем, глобус — это в основе своей шар.

Код примера
beginfig(11);
draw globe(1cm, -15, 0) shifted (-6/2cm, 0); % радиус, западная долгота и северная широта, десятичные
draw globe(3/2cm, -30.28367, 59.93809);
draw globe(4/3cm, -140, -30) shifted (10/3cm, 0);
endfig;
Хотя нет: тут штриховка идет по параллелям, и управлять толщиной штриха для сохранения плотности заливки еще сложнее, чем в случае поперечной штриховки на шлангах, так что это отдельный тип шара.

Код примера
beginfig(12);
draw sphere.l(2cm, -60); % диаметр и широта
draw sphere.l(3cm, 45) shifted (3cm, 0);
endfig;
А гирька — это незамысловатая конструкция из двух видов шлангов переменной толщины.

Код примера
beginfig(13);
draw weight.s(1cm); % высота гирьки
draw weight.s(2cm) shifted (2cm, 0);
endfig;
Еще есть инструмент, чтобы завязывать шланги в узлы.

Код примера, чтобы не загромождать, только один узел
beginfig(14);
path p;
p := (dir(90)*4/3cm) {dir(0)} .. tension 3/2 ..(dir(90 + 120)*4/3cm){dir(90 + 30)} .. tension 3/2 ..(dir(90 - 120)*4/3cm){dir(-90 - 30)} .. tension 3/2 .. cycle;
p := p scaled 6/5;
addStrandToKnot (primeOne) (p, 1/4cm, "l", "1, -1, 1"); % сначала к узлу с именем primeOne добавляется нить, идущая по пути p шириной в 1/4cm, которая будет рисоваться шлангом типа "l" (то есть tube.l, tube.t пока работает плоховато) и будет проходить в в «слоях» "1, -1, 1" в местах пересечений по ходу кривой p
draw knotFromStrands (primeOne); % затем рисуется сам узел. нитей можно добавлять несколько
endfig;
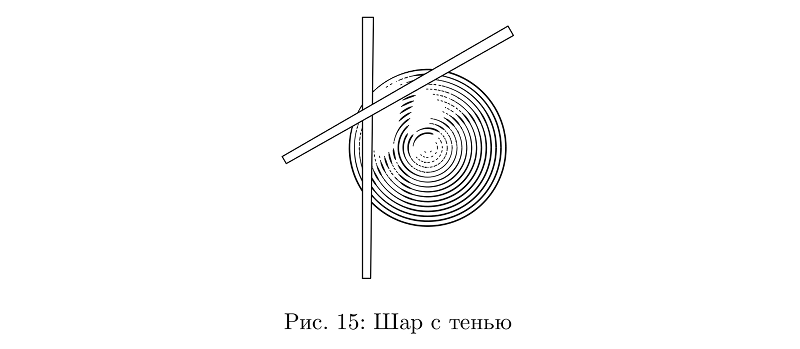
Тени у узлов — некоторое усложнение в модели освещения. В принципе, никто не мешает пользоваться ими и в других случаях, но цели уходить глубоко в объем я себе не ставил, так что пока это и не очень удобно, и не везде работает.

Код примера
beginfig(15);
path shadowPath[];
boolean shadowsEnabled;
numeric numberOfShadows;
shadowsEnabled := true; % тени надо включить
numberOfShadows := 1; % указать их количество
shadowPath0 := (-1cm, -2cm) -- (-1cm, 2cm) -- (-1cm +1/6cm, 2cm) -- (-1cm + 1/8cm, -2cm) -- cycle; % предмет, отбрасывающий тень, плоский и описывается замкнутым контуром
shadowDepth0 := 4/3cm; % располагается на такой-то «высоте» над предметом, на который тень падает
shadowPath1 := shadowPath0 rotated -60;
shadowDepth1 := 4/3cm;
draw sphere.c(2.4cm); % нормально тень пока отбрасывается только на шары sphere.c и шланги tube.l с постоянным сечением
fill shadowPath0 withcolor white;
draw shadowPath0;
fill shadowPath1 withcolor white;
draw shadowPath1;
endfig;
А, еще, конечно, нужна текстура дерева. Влияние характера роста сучков на рисунок срезов годичных колец — тема для серьезного исследования. Очень упрощая, можно представить себе годичные кольца параллельными плоскостями, в которые вносят искажения сучки. Так достаточно описать изменение плоскости какой-нибудь не очень мудреной функцией (функцией сучка) и считать серию изолиний для суммы набора таких функций искомым рисунком годичных колец.

Код примера
beginfig(16);
numeric w, b;
pair A, B, C, D, A', B', C', D';
w := 4cm;
b := 1/2cm;
A := (0, 0);
A' := (b, b);
B := (0, w);
B' := (b, w-b);
C := (w, w);
C' := (w-b, w-b);
D := (w, 0);
D' := (w-b, b);
draw woodenThing(A--A'--B'--B--cycle, 0); % доска, ограниченная контуром A--A'--B'--B--cycle, с волокнами дерева под углом 0 градусов
draw woodenThing(B--B'--C'--C--cycle, 90);
draw woodenThing(C--C'--D'--D--cycle, 0);
draw woodenThing(A--A'--D'--D--cycle, 90);
eyescale := 2/3cm; % масштаб глаза
draw eye(150) shifted 1/2[A,C]; % глаз смотрит в направлении 150 градусов
endfig;
Глаз из картинки выше может немного то открываться, то прищуриваться, и ширина зрачка у него меняется. Смысла особого в этом нет, но так получается более живенько, чем если бы такие мелочи везде были механически одинаковыми.

Код примера
beginfig(17);
eyescale := 2/3cm; % по умолчанию 1/2cm
draw eye(0) shifted (0cm, 0);
draw eye(0) shifted (1cm, 0);
draw eye(0) shifted (2cm, 0);
draw eye(0) shifted (3cm, 0);
draw eye(0) shifted (4cm, 0);
endfig;
Чаще всего картинки были не очень сложные, но если подходить к делу со всей серьезностью, то многие задачи нужно решить, чтобы осмысленно их проиллюстрировать. Вот, скажем, задача Лопиталя о блоке (не знаю, как ее правильно по-русски называют, в учебнике ее не было, здесь просто для примера): висит на веревке длины l, подвешенной в точке A, блок, он зацеплен за другую веревку, подвешенную на той же высоте в точке B, на второй веревке висит груз C. Спрашивается, если веревки и блок невесомы, где окажется груз? На удивление, и решение задачи, и построение не такие уж и элементарные, но зато, играя несколькими переменными, можно легко сделать картинку именно такой, какая будет лучше всего смотреться на полосе, оставаясь при этом правдивой.

Код примера
vardef lHopitalPulley (expr AB, l, m) = % расстояние AB между точками крепления нитей и длины l, m самих нитей. почему без единиц изменения? тут играют роль ограничения метапоста: если дальнейшие вычисления производить с такими большими числами, какими являются в этих краях сантиметры, случится arithmetic overflow.
save A, B, C, D, E, o, a, x, y, d, w, h, support;
image(
pair A, B, C, D, E, o[];
path support;
numeric a, x[], y[], d[], w, h;
x1 := (l**2 + abs(l)*((sqrt(8)*AB)++l))/4AB; % собственно, решение задачи
y1 := l+-+x1; % нахождение второй координаты блока тривиально
y2 := m - ((AB-x1)++y1); % как и нахождение второй координаты груза
A := (0, 0);
B := (AB*cm, 0);
D := (x1*cm, -y1*cm);
C := D shifted (0, -y2*cm);
d1 := 2/3cm; d2 := 1cm; d3 := 5/6d1; % диаметры блока, груза и колеса блока
w := 2/3cm; h := 1/3cm; % ширина краев доски и толщина доски. в принципе, всё это можно вынести в аргументы
o1 := (unitvector(C-D) rotated 90 scaled 1/2d3);
o2 := (unitvector(D-B) rotated 90 scaled 1/2d3);
E := whatever [D shifted o1, C shifted o1]
= whatever [D shifted o2, B shifted o2]; % место, где будет расположен центр блока
a := angle(A-D);
support := A shifted (-w, 0) -- B shifted (w, 0) -- B shifted (w, h) -- A shifted (-w, h) -- cycle;
draw woodenThing(support, 0); % доска, на которой всё висит
draw pulley (d1, a - 90) shifted E; % блок
draw image(
draw A -- D -- B withpen thickpen;
draw D -- C withpen thickpen;
) maskedWith (pulleyOutline shifted E); % нити надо прикрыть блоком
draw sphere.c(d2) shifted C shifted (0, -1/2d2); % грузом служит шар
dotlabel.llft(btex $A$ etex, A);
dotlabel.lrt(btex $B$ etex, B);
dotlabel.ulft(btex $C$ etex, C);
label.llft(btex $l$ etex, 1/2[A, D]);
)
enddef;
beginfig(18);
draw lHopitalPulley (6, 2, 11/2); % теперь можно подставлять такие параметры, с какими иллюстрации будет уютней на полосе
draw lHopitalPulley (3, 5/2, 3) shifted (8cm, 0);
endfig;
А что учебник? Увы и ах, когда уже были готовы почти все иллюстрации и верстка, что-то там случилось и он так и не вышел. Поэтому, наверное, некоторое время спустя я и переписал все основные штуки из получившейся библиотеки заново и выложил код на гитхаб. Какие-то кунштюки туда не вошли: к примеру, электрические схемы или функция для рисования машинок и тракторов. Какие-то — добавились: узлы, например.
Работает вся эта кухня небыстро: на то, чтобы собрать все картинки к этой статье с LuaLaTeX на моем ноутбуке с i5-4200U 1.6 ГГц, уходит примерно минута. Для очень многих вещей используется генератор псевдослучайных чисел, поэтому аналогичные картинки будут выглядеть немного по-разному не только внутри одного прогона (это фича), но и каждый следующий прогон даст картинки, отличные от предыдущего. Но всегда можно выставить в преамбуле
randomseed := какому-то числу, и все одинаковые прогоны станут выдавать одинаковые картинки.