Comments 42
Bring it on —…
Hurt me plenty —…
Nightmare —…
Сегодня им 25 лет ))
спасибо за статью, давно интересно в этом разобраться, но как-то лень, что ли…
Я так полагаю (точнее — надеюсь), предполагается цикл статей для тех, кому тоже лень самим все искать, как мне?
1. Я бы даже более общо ставил бы вопрос — а зачем вообще математику изучать? Математикой пичкают студентов на всех естественно-научных факультетах, и не только на них; даже психологи какие-нибудь вынуждены изучать математику. К сожалению (или к счастью?) это одно из тех немногих орудий, которое человечество имеет в своём арсенале для разгадок тайн природы.
2. Я не ставлю своей целью убедить кого-то изучать математику, поскольку невозможно в человека вложить такую чудовищной силы мотивацию извне. Математика сложная, она трудна, изучать её тяжко и энергозатратно, в жизни для многих есть более интересные занятия. Эта потребность должна идти изнутри, «почему оно так? почему не иначе?». Многими вещами я просто пользуюсь (как потребитель), к примеру, мне не очень интересно, как выращивать ананасы или персики, я их просто ем. Возможно, мне никогда не придётся этим заниматься. Я плохо разбираюсь в том, как работает медицина. Всё изучить невозможно, и надо отсеивать ненужное/неинтересное. Эта статья скорее для тех, кто хочет начать, но не знает, откуда.
3. Кто вам сказал, что это книги для математиков? Практически все книги 1-го уровня — книги для инженеров/программистов, которые исследуют математику как инструмент, а не как предмет изучения. В заглавии некоторых вообще прямым текстом написано «для программистов». Книги для математиков (уровня мехмата) — это книги 3-го уровня.
4. Где я ратую за утилитарность? Мне казалось, что я своим введением а) ясно обозначил, что математика может и не пригодиться в явном виде; б) профит, если и будет, то не сразу и не очевиден; в) в настоящей жизни «силовые» решения чаще продавливают элегантные математические.
5. Библиотеки машинного обучения (в частности, scikit и другие) часто работают хорошо за счет того, что в них уже с самого начала был заложен мощный потенциал умными людьми. Тем не менее, даже они не всегда хорошо работают из коробки. Очевидный пример: линейная регрессия на не-нормированных данных. Да и даже сам выбор модели по данным требует понимания, что теоретически может сработать, а что не «прокатит», как бы вы не подгонялись под ответ.
Очевидный пример: линейная регрессия на не-нормированных данных.
А почему он очевидный? Ведь если ваша цель — зафитить линрег, то вы сможете сделать это и на ненормированных данных.
Если один признак из диапазона 0..1, а второй – из 0..1000000, то решение в лоб будет намного дольше сходиться.
Подбор параметров с помощью градиентного спуска. Функция потерь будет иметь вид длинного оврага, где негде развернуться.
На точность решения через нормальное уравнение ненормированные фичи тоже плохо влияют, особенно если вычисляете псевдообратную матрицу, а не обратную.
Вот я тут проверил даже на регрессии от двух переменных. При разнице диапазонов в миллион решение через псевдобратную матрицу даёт ошибку в третьем знаке. Если нормировать, то всё OK.
Вообще, в численных методах приведение величин к одному диапазону – первое, что делают. Иначе погрешности будут зашкаливать для сколько-нибудь сложного алгоритма.
Кстати, kirtsar, я бы ещё добавил в диаграммку численные методы, раз уж о них заговорили.
Подбор параметров с помощью градиентного спуска.
Ну так вот это не решение в лоб. Это уже нужно, когда речь идет о регуляризации. Решение в лоб именно линейной регрессии — через уравнение.
Вот я тут проверил даже на регрессии от двух переменных. При разнице диапазонов в миллион решение через псевдобратную матрицу даёт ошибку в третьем знаке. Если нормировать, то всё OK.
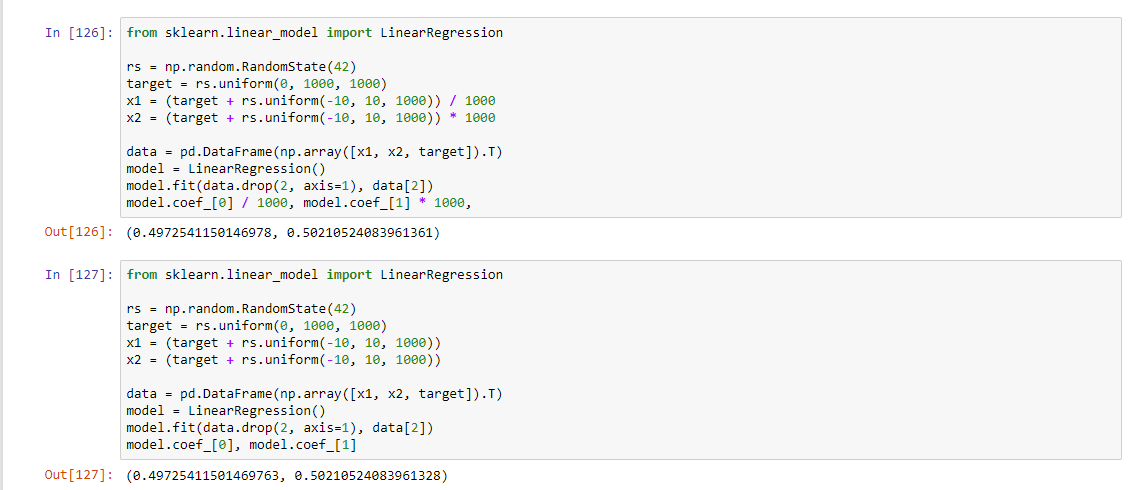
Разница в коэффициентах в тринадцатом знаке. Это реальный пример реального использования линрега в лоб на ненормированных фичах.
А вот разница в скорости работы в этом же примере:

Скорость с отнормированными фичами лучше, но в пределах погрешности.
Вообще, в численных методах приведение величин к одному диапазону – первое, что делают. Иначе погрешности будут зашкаливать для сколько-нибудь сложного алгоритма.
Обычно я бы никогда не сказал такой, на первый взгляд, бред, но в контексте ваших слов скажу: машинное обучение — это не численные методы. То расхождение, ради которого вы нормируете величины, в реальных задачах ML не выстрелит, если мы всё ещё говорим про пример с линрегом.
Нам в головы на матстате вдалбливают, что перед регрессией фичи надо нормализовывать. Но на практике это нужно в двух конкретных случаях: регуляризация и интерпретируемость.
Поэтому мне показалось забавным, что автор привел именно это полузаблуждение в качестве примера того, где математика нужна в ML.
Расчехляю sklearn, который автор привел в пример
Не очень удачный пример, так как метод fit как раз нормализует фичи перед непосредственно вычислениями.
Поэтому у вас результаты одинаковые и получались, так как нормализация, фактически, была в обоих случаях.
Нормализация по умолчанию стоит в False.
Что ж, был невнимателен, согласен. (Впрочем, fit центрирует данные, так что предобработка всё же выполняется.)
Не буду спорить, что в sklearn (а точнее, его LAPACK-бэкэнде) алгоритм решения работает как надо. Но повторюсь, что если решать совсем-совсем в лоб, то масштаб влияет сильнее за счёт накопления погрешностей в алгоритмах.

Но если вы учите простой линрег с целью получить предсказание, то вроде бы и нормировать необязательно.
а зачем вообще математику изучать?
Математику уже затем изучать нужно, что она ум в порядок приводит. М.В. Ломоносов.
Другой пример (не знаю, насколько удачный), когда надо понимать механизмы под капотом – применение линейной регрессии из sklearn «в лоб», когда фичи зависимы.
когда знание математики помогает лучше и проще решить задачу, чем перебор гиперпараметров и нагромождение ансамблей.
Как вам такая теория, что нужно знать математику, чтобы разумно перебирать гиперпараметры и правильно тюнить модели в ансамбль?
Ну и у Гилберта Стренга есть еще более практически ориентированные курсы:
А еще и книга «Computational Science and Engineering» к этим курсам.
Где бы только столько времени на это все найти…
С теорвером сложно, поэтому решил отдельно вынести. Особенно с байесовским подходом — на русском вообще почти ничего не встречал, кроме упоминаний в учебниках по классической статистике.
Курсы хорошие, но там есть и такие вещи, наподобие численных решений всяческих диф. уравнений или расчёта электрических цепей. Я боюсь, что если вникать ещё и в эти (безусловно важные) области приложения линейной алгебры, то можно и не выкарабкаться никогда )) хотя наверное стоило упомянуть.
мир не устроен по законам математикиНе слишком ли категоричное утверждение? Простейший пример для школьника: дан диаметр круглой площадки, нужно найти количество досок, чтобы сделать глухой забор по окружности. Далее можно приводить примеры из физики, которая почему-то вся на математике ;)
Мир не устроен по законам математики
Тут слегка перевернуто с ног на голову.
- Не факт что мир вообще устроен по каким-то законам, неважно физический, экономический или химию взять,
- Тем не менее, математика призвана мир описывать, а машинное обучение как и весь data science — про то, как наблюдения (мира) собственно в саму математику уложить.
То что модели работают, пусть и не 100%, говорит о том что математика все же что-то описывает (где-то на процент своей точности), — с точки зрения математики опять же.
Но этого достаточно, чтобы например воспроизвести процесс с достаточным для употребления (персиков, ананасов и других) результатов человеком.
Тут не то чтобы курояичность, тут как бы универсальней математики у человека для работы с наблюдениями каких бы то ни было инструментов с предсказательной силой нет. С конкретно же описаниями разговорный язык лучше справляется…
Есть физическая модель, некое решение. И есть наша действительность, о которой что-либо узнать можно лишь посредством эксперимента. Решение точно тогда и только тогда, когда для любого входного значения, результат решения равен наблюдению эксперимента. Учитывая размеры пространства и неточность измерительных приборов доказать точность решения невозможно.
Учитывая размеры пространства и неточность измерительных приборов доказать точность решения невозможно.Для количественных задач. А в качественной — среда щелочная или нет, т.е. без цвета или красный — высокой точности не нужно. Аналогично: какой свет на светофоре: зеленый или красный. На практике и в количественных задачах задаются разумной точностью. Так земельный участок, ограниченный окружностью диаметром 20 м, будет ограничен «не точной окружностью», нпр., где-то на см меньше, а где-то больше. И это обычно устраивает.
Да, опытный программист может много чего написать без представления о математики.
Но по моим наблюдениям, основная проблема в IT сейчас — низкая надежность софта. Основная идея математики — доказательство. Она так же предоставляет мощные инструменты для этого — формальную логику, теорию множеств, теорию типов. Если бы программисты взяли на вооружение эту идею (что правильность программы хорошо бы доказать) и инструменты (хотя бы перешли на языки с хорошей типизацией), проблема надежности стала бы не такой острой.
П.С. На тему гордости за дом без гвоздей — Building Without Nails The Genius of Japanese Carpentry
Handbook of Linear Algebra
www.amazon.com/Handbook-Algebra-Discrete-Mathematics-Applications/dp/1138199893
А по матану нравится
Modern Engineering Mathematics
www.amazon.com/Modern-Engineering-Mathematics-Always-learning/dp/1292080736
Advanced Modern Engineering Mathematics
www.amazon.com/Advanced-Modern-Engineering-Mathematics-James/dp/129217434X
Линал — Кострикин-Манин (и только он!)
Calculus — Зорич 1-ый том
Топология — Виро-Нецветаев-Харламов-Иванов
Analysis — Львовский, Шварц
Фихтенгольца, возможно, полезно почитать в старших классах, но вообще его место на свалке истории.
(Насколько мне известно, нынешний мехмат чрезвычайно слаб, по крайней мере если сравнивать его с матмехом, нму, матфаком)
Это был комментарий к «Nightmare»
Кострикина-Манина без базы из курса «Общей алгебры» тяжеловато будет читать. Весь Ленг здесь действительно не нужен, но его нельзя не упомянуть, так как это лучший учебник алгебры.
И добавлю, что в Зориче нету теории меры и интеграла Лебега, которая необходима для ТВ.
С НМУ сравнивать не буду, очевидно там математика гораздо сильнее (чем на любом математическом факультете любого российского вуза, уровень слушателей позволяет).
Про теорвер думаю попозже расписать, в части 2. С теорией меры всё сложно: с одной стороны кажется, что без неё нормально не изложить теорию вероятностей (те же условные мат. ожидания), с другой — слишком это абстрактные вещи, чтобы в них лезть в такой прикладной области.
Со временем там произошли неприятные метаморфозы (I, II, Обсуждение), и в итоге его уровень заметно упал. Тем не менее, олимпиадники и матшкольники предпочитают матфак. Если даже посмотреть на студентов НМУ, параллельно учащихся в вышке, и сравнить их с НМУшниками-мехматянами, то у первых уровень заметно выше. Вот что говорит о матфаке и мехмате один из преподавателей пресловутой кафедры матана МГУ.
Дорожная карта математических дисциплин для машинного обучения, часть 1