Рассмотрим прогнозирование временных рядов. Попытаемся спрогнозировать графики котировок, или что-нибудь другое, что под руку подвернется.

Возьмем за основу прогнозирование представленное в статье Модель прогнозирования временных рядов по выборке максимального подобия: пояснение и пример (эта статья не моя). Краткая суть там в том, что ищется наиболее подобный отрезок графика слева от прогноза среди прошлой истории, и от этого старого лучшего потом берутся значения справа от графика и используются как прогноз.
Я пойду дальше. При расчете прогноза буду брать не один лучший по корреляции случай, а пачку лучших. И прогнозом будет средняя от результатов по этой пачке. Это даст возможность понимать, что найденное значение это закономерность, а не случайное совпадение с нужным прогнозом, или случайным отклонением, если прогноз отклоняется от фактического.
Использование единичного лучшего варианта как в той статье не является корректным, так же как определять распределение вероятностей одним значением из этого распределения. Если сгенерировать очень большой график случайных данных, и запустить по ним поиск, то в них обязательно найдутся коррелирующие отрезки, и даже возможно с коэффициентом 0.9999, но это совсем не обязательно, что за этими отрезками дальше будут следовать так же подобные продолжения — оно по прежнему все рандомно. И нужно взять именно пачку таких отрезков и посчитать, что дисперсия последующих данных ниже дисперсии, которая образуется от случайной выборки из этих данных. И если дисперсия пачки ниже — вот тогда это прогноз. Хотя это то же не до конца точное представление возможных ошибок, но пока этого хватит.
Т.е. прогнозирование это не то, какой принцип выборки и корреляции сравниваемых отрезков используем, главное что бы в результате применения этой выборки, дисперсия искомых значений была меньше, чем в результате случайной выборки.
Так же дисперсия этой пачки даст возможность оценивать какой лучше использовать вариант отбора среди предыдущих случаев. Ведь отбирать можно не по одному всегда отрезку коррелирующих данных, и не всегда использовать корреляцию Пирсона. И такой выбор можно делать для каждой прогнозируемой точки отдельно. Для какого типа выборки дисперсия меньше, тот вариант и лучше для текущей точки.
Каков размер пачки должен быть? Это упирается в вопрос доверительных интервалов. Что бы не очень загружаться, есть упоминание, что для определения среднего значения лучше брать не меньше 30 примеров. В случае наличия избытка тестовых данных, я бы брал не меньше 100.
Соотношение стандартных отклонений выборки по алгоритму и выборки случайной можно назвать теоретическим коэффициентом удачности прогнозирующего алгоритма для текущей точки для целей сравнения с другими алгоритмами выборки, или для определения полезности вообще этого прогноза, пока самого фактического значения еще нет.
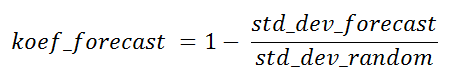
Этот коэффициент может принимать в некоторых случаях отрицательные значений. Те точки, в которых это происходит, они малоинтересны, так же как и точки с нулевым коэффициентом. В случае 100% прогнозируемости он будет равен единице.
Перейдем к практическим примерам, опять же из той статьи. После исправления тамошних мелких ошибочек получаем согласное той статье и тому алгоритму следующий результат:
расчет прогноза на момент 9/1/2012 23:00 позиция 52631
всего проверено значений на подобие 2184
самая лучшая корреляция 0.958174 позиция 52295
коэффициенты переноса alpha(1/2) 1.03117 -11.1992
ошибка прогноза от факта mape 5.210%
mape — термин из исходной статьи Mean Absolute Percentage Error, считается по формуле
Abs(Прогноз — Факт)/Факт
А теперь сделаем выборку не одного лучшего подобия, а пачки лучших и все для прогнозирования одного момента времени и посмотрим что получается:
0 corr 0.958174 pos 52295 mape 5.210%
1 corr 0.953571 pos 52151 mape 6.566%
2 corr 0.953532 pos 45599 mape 11.642%
3 corr 0.951462 pos 45743 mape 7.033%
4 corr 0.950921 pos 45575 mape 3.300%
5 corr 0.950789 pos 38687 mape 3.538%
Значение корреляции здесь меняется от значения к значению ничтожно. В то же время, значение результата прогноза меняется от 3% до 11%. Т.е. те изначальные 5% это ничто иное как просто случайность, могло бы быть и 11% и 3%.
При указанных в той статье условиях выборки на подобие, всего сравниваться могут 2184 значений. Из них я взял пачку лучших в 1500 штук, отсортировал в порядке уменьшения корреляции, и отобразил это в виде графика. Корреляция в этой пачке от лучших 0.958 упала до 0.715 слева на право. А вот колебания результата практически не менялось:
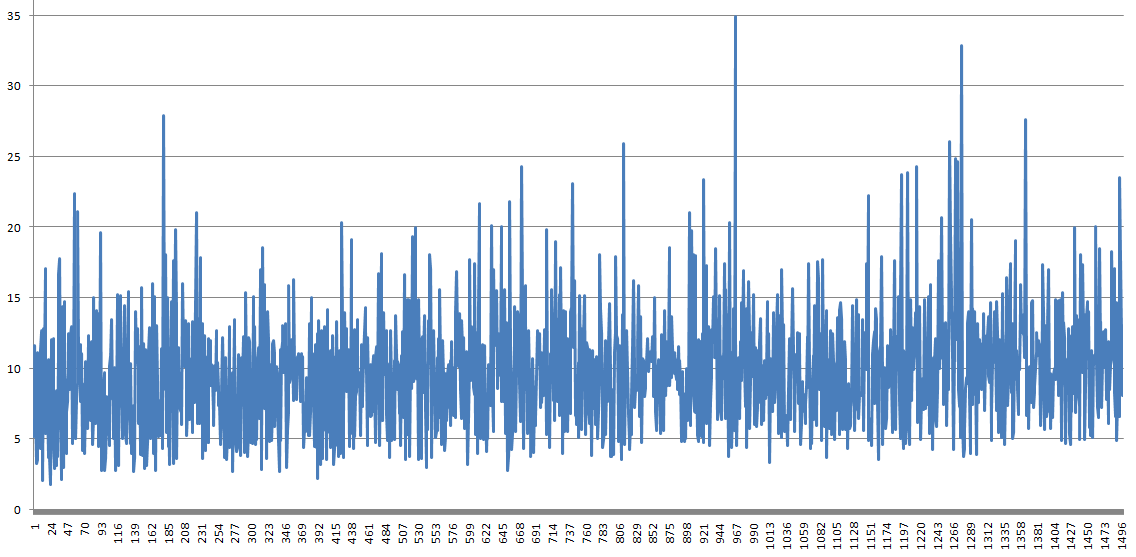
Видно, что зависимость результата от корреляции очень низкая, но тем не менее кажется есть. В общем возьмем пачку в 100 лучших значений, и посчитаем прогноз, как я упоминал, по средней по этой пачке. Результат следующий: mape 5.824%, stddev mape 7.035%. Но эти 5.8% это уже не случайное совпадение, а среднее от распределения — наиболее вероятный прогноз. Стандартное отклонение mape превышает сам mape, но это потому что mape имеет не симметричное распределение.
Так же посчитал такой же прогноз но по условно случайной выборке, точнее просто усреднено от всех возможных вариантов, результат mape 8.246%. По случайной выборке ошибка чуть больше, но эта величина все равно в пределах того разброса, который посчитался от выборки лучших. Для обсчитываемой точки, обозначенный мной коэффициент теоретического прогнозирования близок к нулю, точнее koef_forecast = -0.041. Я его считал не от stddev mape (он включает фактический прогноз), а от абсолютных значений прогноза, если будете смотреть программу то там приводятся исходные цифры для него.
Но это если касательно временной отметки, про которую говорилось в исходной статье. А вот если взять скажем «9/4/2012 23:00» (месяц/день/год время), то там теоретический коэффициент полезности составляет koef_forecast = 0.21, а mape = 3.126%, mape_rand = 7.147%. Т.е. koef_forecast заранее показал, что текущая точка будет посчитана точнее, чем прежняя. Суть полезности этого коэффициента в том, что можно хоть как-то оценить результат еще до получения фактических данных, т.к. фактические данные в нем не участвуют. Чем выше он, тем лучше. Я уже упоминал, что абсолютно прогнозируемая точка будет иметь коэффициентом единицу.
Вы сами можете посмотреть как меняются все эти цифры в моей демонстрационной программке на Qt C++, там можно выбрать и дату и размер пачки: исходники на github
Отбор лучших значений производится по следующему алгоритму:
Смысл сюда постить весь исходник нет, там он не сложный, и с комментариями. Основа в процедуре MainWindow::to_do_test() в файле mainwindow.cpp.
Пока все, продолжу попытки что-нибудь спрогнозировать в следующей части.
PS. Пожалуйста, оставляйте ваши комментарии, на предмет все ли понятно, чего не хватает. У меня уже сформирован примерный план, что дальше написать, но с вашими комметариями я это сделаю лучше.

Возьмем за основу прогнозирование представленное в статье Модель прогнозирования временных рядов по выборке максимального подобия: пояснение и пример (эта статья не моя). Краткая суть там в том, что ищется наиболее подобный отрезок графика слева от прогноза среди прошлой истории, и от этого старого лучшего потом берутся значения справа от графика и используются как прогноз.
Я пойду дальше. При расчете прогноза буду брать не один лучший по корреляции случай, а пачку лучших. И прогнозом будет средняя от результатов по этой пачке. Это даст возможность понимать, что найденное значение это закономерность, а не случайное совпадение с нужным прогнозом, или случайным отклонением, если прогноз отклоняется от фактического.
Использование единичного лучшего варианта как в той статье не является корректным, так же как определять распределение вероятностей одним значением из этого распределения. Если сгенерировать очень большой график случайных данных, и запустить по ним поиск, то в них обязательно найдутся коррелирующие отрезки, и даже возможно с коэффициентом 0.9999, но это совсем не обязательно, что за этими отрезками дальше будут следовать так же подобные продолжения — оно по прежнему все рандомно. И нужно взять именно пачку таких отрезков и посчитать, что дисперсия последующих данных ниже дисперсии, которая образуется от случайной выборки из этих данных. И если дисперсия пачки ниже — вот тогда это прогноз. Хотя это то же не до конца точное представление возможных ошибок, но пока этого хватит.
Т.е. прогнозирование это не то, какой принцип выборки и корреляции сравниваемых отрезков используем, главное что бы в результате применения этой выборки, дисперсия искомых значений была меньше, чем в результате случайной выборки.
Так же дисперсия этой пачки даст возможность оценивать какой лучше использовать вариант отбора среди предыдущих случаев. Ведь отбирать можно не по одному всегда отрезку коррелирующих данных, и не всегда использовать корреляцию Пирсона. И такой выбор можно делать для каждой прогнозируемой точки отдельно. Для какого типа выборки дисперсия меньше, тот вариант и лучше для текущей точки.
Каков размер пачки должен быть? Это упирается в вопрос доверительных интервалов. Что бы не очень загружаться, есть упоминание, что для определения среднего значения лучше брать не меньше 30 примеров. В случае наличия избытка тестовых данных, я бы брал не меньше 100.
Соотношение стандартных отклонений выборки по алгоритму и выборки случайной можно назвать теоретическим коэффициентом удачности прогнозирующего алгоритма для текущей точки для целей сравнения с другими алгоритмами выборки, или для определения полезности вообще этого прогноза, пока самого фактического значения еще нет.
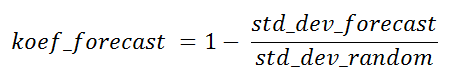
Этот коэффициент может принимать в некоторых случаях отрицательные значений. Те точки, в которых это происходит, они малоинтересны, так же как и точки с нулевым коэффициентом. В случае 100% прогнозируемости он будет равен единице.
Перейдем к практическим примерам, опять же из той статьи. После исправления тамошних мелких ошибочек получаем согласное той статье и тому алгоритму следующий результат:
расчет прогноза на момент 9/1/2012 23:00 позиция 52631
всего проверено значений на подобие 2184
самая лучшая корреляция 0.958174 позиция 52295
коэффициенты переноса alpha(1/2) 1.03117 -11.1992
ошибка прогноза от факта mape 5.210%
mape — термин из исходной статьи Mean Absolute Percentage Error, считается по формуле
Abs(Прогноз — Факт)/Факт
А теперь сделаем выборку не одного лучшего подобия, а пачки лучших и все для прогнозирования одного момента времени и посмотрим что получается:
0 corr 0.958174 pos 52295 mape 5.210%
1 corr 0.953571 pos 52151 mape 6.566%
2 corr 0.953532 pos 45599 mape 11.642%
3 corr 0.951462 pos 45743 mape 7.033%
4 corr 0.950921 pos 45575 mape 3.300%
5 corr 0.950789 pos 38687 mape 3.538%
Значение корреляции здесь меняется от значения к значению ничтожно. В то же время, значение результата прогноза меняется от 3% до 11%. Т.е. те изначальные 5% это ничто иное как просто случайность, могло бы быть и 11% и 3%.
При указанных в той статье условиях выборки на подобие, всего сравниваться могут 2184 значений. Из них я взял пачку лучших в 1500 штук, отсортировал в порядке уменьшения корреляции, и отобразил это в виде графика. Корреляция в этой пачке от лучших 0.958 упала до 0.715 слева на право. А вот колебания результата практически не менялось:

Видно, что зависимость результата от корреляции очень низкая, но тем не менее кажется есть. В общем возьмем пачку в 100 лучших значений, и посчитаем прогноз, как я упоминал, по средней по этой пачке. Результат следующий: mape 5.824%, stddev mape 7.035%. Но эти 5.8% это уже не случайное совпадение, а среднее от распределения — наиболее вероятный прогноз. Стандартное отклонение mape превышает сам mape, но это потому что mape имеет не симметричное распределение.
Так же посчитал такой же прогноз но по условно случайной выборке, точнее просто усреднено от всех возможных вариантов, результат mape 8.246%. По случайной выборке ошибка чуть больше, но эта величина все равно в пределах того разброса, который посчитался от выборки лучших. Для обсчитываемой точки, обозначенный мной коэффициент теоретического прогнозирования близок к нулю, точнее koef_forecast = -0.041. Я его считал не от stddev mape (он включает фактический прогноз), а от абсолютных значений прогноза, если будете смотреть программу то там приводятся исходные цифры для него.
Но это если касательно временной отметки, про которую говорилось в исходной статье. А вот если взять скажем «9/4/2012 23:00» (месяц/день/год время), то там теоретический коэффициент полезности составляет koef_forecast = 0.21, а mape = 3.126%, mape_rand = 7.147%. Т.е. koef_forecast заранее показал, что текущая точка будет посчитана точнее, чем прежняя. Суть полезности этого коэффициента в том, что можно хоть как-то оценить результат еще до получения фактических данных, т.к. фактические данные в нем не участвуют. Чем выше он, тем лучше. Я уже упоминал, что абсолютно прогнозируемая точка будет иметь коэффициентом единицу.
Вы сами можете посмотреть как меняются все эти цифры в моей демонстрационной программке на Qt C++, там можно выбрать и дату и размер пачки: исходники на github
Отбор лучших значений производится по следующему алгоритму:
inline void OrdPack::add_value(double koef, int i_pos) {
if (std::isfinite(koef)==false) return;
if (koef <= 0.0) return;
if (mmap_ord.size() < ma_count_for_pack) {
if (mmap_ord.size()==0)
mi_koef = koef;
mi_koef = std::min(mi_koef, koef);
mmap_ord.insert({-koef,i_pos});
} else if (koef > mi_koef) {
mmap_ord.insert({-koef,i_pos});
while (mmap_ord.size() > ma_count_for_pack)
mmap_ord.erase(--mmap_ord.end());
mi_koef = -(--mmap_ord.end())->first;
}
}
Смысл сюда постить весь исходник нет, там он не сложный, и с комментариями. Основа в процедуре MainWindow::to_do_test() в файле mainwindow.cpp.
Пока все, продолжу попытки что-нибудь спрогнозировать в следующей части.
PS. Пожалуйста, оставляйте ваши комментарии, на предмет все ли понятно, чего не хватает. У меня уже сформирован примерный план, что дальше написать, но с вашими комметариями я это сделаю лучше.