How to become an author
Search
Write a publication
Pull to refresh

Julia и оптимизация

Reading time9 min
Views4.5K
Julia*Machine learning*Programming*
Tutorial


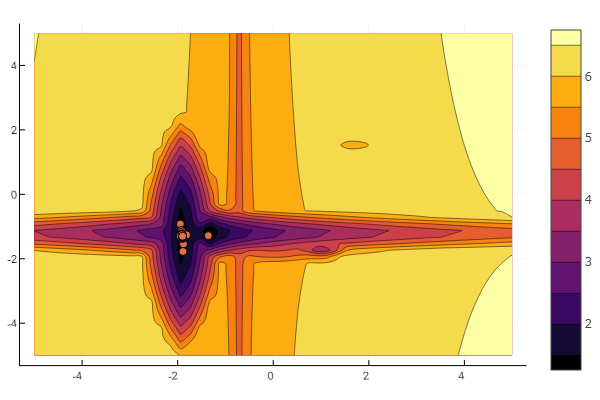
Пришло время рассмотреть пакеты предоставляющие методы решения задач оптимизации. Очень много проблем можно свести к поиску минимума некоторой функции, поэтому следует иметь в арсенале парочку-другую солверов, а уж тем более целый пакет.


Вступление


Язык Julia продолжает набирать популярность. На https://juliacomputing.com можно посмотреть, почему этот язык выбирают астрономы, робототехники и финансисты, а на https://academy.juliabox.com можете начать бесплатные курсы по изучению языка и применению его в во всяком там машинлёнинге. Тем же, кто всерьёз надумал начать учиться советую просмотреть видео, почитать статьи и пощёлкать юпитерские ноутбуки на https://julialang.org/learning/ или хотя бы пройтись по хабу снизу вверх: там будет и установка, и возможности, и применение к делам насущным. А теперь приступим к библиотекам.


BlackBoxOptim


BlackBoxOptim — пакет глобальной оптимизации для Юлии (http://julialang.org/). Он поддерживает как многоцелевые, так и одноцелевые задачи оптимизации и ориентирован на (мета) эвристические / стохастические алгоритмы (DE, NES и т. Д.), которые НЕ требуют, чтобы оптимизируемая функция была дифференцируемой, в отличие от более традиционных, детерминированных алгоритмов, которые часто основаны на градиентах / дифференцируемости. Он также поддерживает параллельные вычисления для ускорения оптимизации функций, которые оцениваются медленно.


Загружаем и подключаем библиотеку


]add BlackBoxOptim
using BlackBoxOptim

Задаём функцию Розенброка:


f(x) = (1.0 - x[1])^2 + 100.0 * (x[2] - x[1]^2)^2

Ищем минимум на отрезке (-5;5) для каждой координаты для двумерной задачи:


res = bboptimize(f; SearchRange = (-5.0, 5.0), NumDimensions = 2)

На что последует ответ:


Starting optimization with optimizer DiffEvoOpt{FitPopulation{Float64},RadiusLimitedSelector,BlackBoxOptim.AdaptiveDiffEvoRandBin{3},RandomBound{RangePerDimSearchSpace}}
0.00 secs, 0 evals, 0 steps

Optimization stopped after 10001 steps and 0.12400007247924805 seconds
Termination reason: Max number of steps (10000) reached
Steps per second = 80653.17866385692
Function evals per second = 81628.98454510146
Improvements/step = 0.2087
Total function evaluations = 10122

Best candidate found: [1.0, 1.0]

Fitness: 0.000000000

и еще много неудобочитаемых данных, но минимум нашелся. Так как используется стохастика, вызовов функции будет многовато, так что для многомерных задач лучше использовать подбор методов


function rosenbrock(x)
  return( sum( 100*( x[2:end] - x[1:end-1].^2 ).^2 + ( x[1:end-1] - 1 ).^2 ) )
end

res = compare_optimizers(rosenbrock; SearchRange = (-5.0, 5.0), NumDimensions = 30, MaxTime = 3.0);

Convex


Convex — это пакет Julia для Disciplined Convex Programming (дисциплинарного выпуклого программирования?). Convex.jl может решать линейные программы, смешанные целочисленные линейные программы и DCP-совместимые выпуклые программы, используя различные решатели, включая Mosek, Gurobi, ECOS, SCS и GLPK, через интерфейс MathProgBase. Он также поддерживает оптимизацию с комплексными переменными и коэффициентами.


using Pkg # просто другой способ загрузки пакетов
Pkg.add("Convex")
Pkg.add("SCS")

На сайте есть много примеров: Томография (процесс восстановления распределения плотности по заданным интегралам по участкам распределения. Например можно работать с томографией на черно-белых изображениях), максимизация энтропии, логистическая регрессия, линейное программирование и т. д.


Например нужно удовлетворить условиям:


$\begin{array}{ll} \mbox{satisfy} & \| x \|_2 \leq 100 \\ & e^{x_1} \leq 5 \\ & x_2 \geq 7 \\ & \sqrt{x_3 x_4} \geq x_2 \end{array}$


using Convex, SCS, LinearAlgebra

x = Variable(4)
p = satisfy(norm(x) <= 100, exp(x[1]) <= 5, x[2] >= 7, geomean(x[3], x[4]) >= x[2])
solve!(p, SCSSolver(verbose=0))
println(p.status)
x.value

Даст ответ


Optimal
4×1 Array{Float64,2}:
  0.0              
  8.554892320716046
 15.329934133156783
 15.329934133156783

JuMP



JuMP является предметно-ориентированным языком моделирования для математической оптимизации, встроенным в Julia. В настоящее время он поддерживает ряд открытых и коммерческих солверов (Artelys Knitro, BARON, Bonmin, Cbc, Clp, Couenne, CPLEX, ECOS, FICO Xpress, GLPK, Gurobi, Ipopt, MOSEK, NLopt, SCS).


JuMP позволяет легко определять и решать задачи оптимизации без экспертных знаний, но в то же время позволяет экспертам внедрять передовые алгоритмические методы, такие как использование эффективных «горячих» стартов в линейном программировании или использование обратных вызовов для взаимодействия с решателями ветвей и границ. JuMP также быстр — бенчмаркинг показал, что он может справляться с вычислениями на скоростях, аналогичных специализированным коммерческим инструментам, таким как AMPL, при сохранении выразительности универсального языка программирования высокого уровня. JuMP может быть легко встроен в сложные рабочие процессы, включая симуляции и веб-серверы.


Данный инструмент позволяет без глубоких знаний справляться с такими задачами как:


  • LP = линейное программирование
  • QP = квадратичное программирование
  • SOCP = коническое программирование второго порядка (включая задачи с выпуклыми квадратичными ограничениями и / или целью)
  • MILP = Смешанное целочисленное линейное программирование
  • НЛП = Нелинейное программирование
  • MINLP = смешанно-целочисленное нелинейное программирование
  • SDP = полуопределенное программирование
  • MISDP = смешанно-целочисленное полуопределенное программирование

Разбора его возможностей хватит на несколько статей, поэтому пока перейдем к следующему:


Optim


Optim Есть много решателей, доступных как из бесплатных, так и из коммерческих источников, и многие уже обернуты для использования в Julia. Немногие из них написаны на этом языке. С точки зрения производительности это редко является проблемой, так как они часто пишутся либо на Fortran, либо на C. Однако решатели, написанные непосредственно на Julia, действительно имеют некоторые преимущества.


При написании программного обеспечения (пакетов) Julia, для которого требуется что-то оптимизировать, программист может либо написать свою собственную процедуру оптимизации, либо использовать один из многих доступных решателей. Например, это может быть что-то из набора NLOpt. Это означает добавление зависимости, которая не написана в Julia, и необходимо сделать больше предположений относительно среды, в которой находится пользователь. Есть ли у пользователя надлежащие компиляторы? Можно ли использовать код GPL в проекте?


Также верно и то, что использование решателя, написанного на C или Fortran, делает невозможным использование одного из главных преимуществ Julia: множественная диспетчеризация. Поскольку Optim полностью написан на языке Julia, в настоящее время мы можем использовать систему диспетчеризации, чтобы упростить использование пользовательских преднастроек. Планируемая особенность в этом направлении заключается в том, чтобы позволить управляемый пользователем выбор решателей для различных этапов алгоритма, полностью основанный на диспетчеризации, а не на предопределенных возможностях, выбранных разработчиками Optim.


Пакет на Julia также означает, что Optim имеет доступ к функциям автоматического дифференцирования через пакеты в JuliaDiff.


Руководство


Приступим:


]add Optim
using Optim

# функция Розенброка
f(x) = (1.0 - x[1])^2 + 100.0 * (x[2] - x[1]^2)^2

x0 = [0.0, 0.0]
optimize(f, x0)

Получим ответ с удобным отчетом:


Results of Optimization Algorithm
 * Algorithm: Nelder-Mead # по умолчанию
 * Starting Point: [0.0,0.0]
 * Minimizer: [0.9999634355313174,0.9999315506115275]
 * Minimum: 3.525527e-09
 * Iterations: 60
 * Convergence: true
   *  √(Σ(yᵢ-ȳ)²)/n < 1.0e-08: true
   * Reached Maximum Number of Iterations: false
 * Objective Calls: 118

А сравним-ка с моим Нелдером-Мидом!


спойлер

Мой окажется медленнее :(


Упрятано
using BenchmarkTools

@benchmark optimize(f, x0)

BenchmarkTools.Trial: 
  memory estimate:  11.00 KiB
  allocs estimate:  419
  --------------
  minimum time:     39.078 μs (0.00% GC)
  median time:      43.420 μs (0.00% GC)
  mean time:        53.024 μs (15.02% GC)
  maximum time:     59.992 ms (99.83% GC)
  --------------
  samples:          10000
  evals/sample:     1

По ходу проверки еще и выяснилось, что моя реализация не работает, если использовать начальным приближением (0, 0). В качестве критерия остановки можно использовать объем симплекса, у меня же используется норма матрицы составленной из вершин. Здесь можно почитать про геометрическую интерпретацию нормы. В обоих случаях получается матрица из нулей — частный случай вырожденной матрицы, поэтому метод не выполняет ни одного шага. Вы можете настроить создание стартового симплекса, например, задавая удаленность его вершин от начального приближения (а не как у меня — половина длины вектора, фу, какой позор...), тогда настройка метода будет более гибкой, либо проследить, чтобы все вершины не сидели в одной точке:


    for i = 1:N+1
        Xx[:,i] = fit
    end

    for i = 1:N
        Xx[i,i] += 0.5*vecl(fit) + ε
    end

Ну да, мой симплекс горааааздо медленнее:


ofNelderMid(fit = [0, 0.])

step= 118 7.7234e-5 f = 2.797-18 x = [1.0, 1.0]

@benchmark ofNelderMid(fit = [0., 0.])

BenchmarkTools.Trial: 
  memory estimate:  394.03 KiB
  allocs estimate:  6632
  --------------
  minimum time:     717.221 μs (0.00% GC)
  median time:      769.325 μs (0.00% GC)
  mean time:        854.644 μs (5.04% GC)
  maximum time:     50.429 ms (98.01% GC)
  --------------
  samples:          5826
  evals/sample:     1

Теперь больше резона вернуться к изучению пакета


Можно выбирать используемый метод:


optimize(f, x0, LBFGS())

Results of Optimization Algorithm
 * Algorithm: L-BFGS
 * Starting Point: [0.0,0.0]
 * Minimizer: [0.9999999926662504,0.9999999853325008]
 * Minimum: 5.378388e-17
 * Iterations: 24
 * Convergence: true
   * |x - x'| ≤ 0.0e+00: false 
     |x - x'| = 4.54e-11 
   * |f(x) - f(x')| ≤ 0.0e+00 |f(x)|: false
     |f(x) - f(x')| = 5.30e-03 |f(x)|
   * |g(x)| ≤ 1.0e-08: true 
     |g(x)| = 9.88e-14 
   * Stopped by an increasing objective: false
   * Reached Maximum Number of Iterations: false
 * Objective Calls: 67
 * Gradient Calls: 67

и получить на него детальную документацию и ссылочки на литературу


?LBFGS()

Можно задать Якобиан и Гессиан функции


function g!(G, x)
    G[1] = -2.0 * (1.0 - x[1]) - 400.0 * (x[2] - x[1]^2) * x[1]
    G[2] = 200.0 * (x[2] - x[1]^2)
end

function h!(H, x)
    H[1, 1] = 2.0 - 400.0 * x[2] + 1200.0 * x[1]^2
    H[1, 2] = -400.0 * x[1]
    H[2, 1] = -400.0 * x[1]
    H[2, 2] = 200.0
end

optimize(f, g!, h!, x0)

Results of Optimization Algorithm
 * Algorithm: Newtons Method
 * Starting Point: [0.0,0.0]
 * Minimizer: [0.9999999999999994,0.9999999999999989]
 * Minimum: 3.081488e-31
 * Iterations: 14
 * Convergence: true
   * |x - x'| ≤ 0.0e+00: false 
     |x - x'| = 3.06e-09 
   * |f(x) - f(x')| ≤ 0.0e+00 |f(x)|: false
     |f(x) - f(x')| = 3.03e+13 |f(x)|
   * |g(x)| ≤ 1.0e-08: true 
     |g(x)| = 1.11e-15 
   * Stopped by an increasing objective: false
   * Reached Maximum Number of Iterations: false
 * Objective Calls: 44
 * Gradient Calls: 44
 * Hessian Calls: 14

Как видно, автоматически отработал метод Ньютона. А вот так можно задать область поиска и воспользоваться градиентным спуском:


lower = [1.25, -2.1]
upper = [Inf, Inf]
initial_x = [2.0, 2.0]
inner_optimizer = GradientDescent()
results = optimize(f, g!, lower, upper, initial_x, Fminbox(inner_optimizer))

Results of Optimization Algorithm
 * Algorithm: Fminbox with Gradient Descent
 * Starting Point: [2.0,2.0]
 * Minimizer: [1.2500000000000002,1.5625000000000004]
 * Minimum: 6.250000e-02
 * Iterations: 8
 * Convergence: true
   * |x - x'| ≤ 0.0e+00: true 
     |x - x'| = 0.00e+00 
   * |f(x) - f(x')| ≤ 0.0e+00 |f(x)|: true
     |f(x) - f(x')| = 0.00e+00 |f(x)|
   * |g(x)| ≤ 1.0e-08: false 
     |g(x)| = 5.00e-01 
   * Stopped by an increasing objective: false
   * Reached Maximum Number of Iterations: false
 * Objective Calls: 84382
 * Gradient Calls: 84382

Ну или не знаю, скажем, Вы захотели решить уравнение


f_univariate(x) = 2x^2+3x+1

optimize(f_univariate, -2.0, 1.0)

Results of Optimization Algorithm
 * Algorithm: Brents Method
 * Search Interval: [-2.000000, 1.000000]
 * Minimizer: -7.500000e-01
 * Minimum: -1.250000e-01
 * Iterations: 7
 * Convergence: max(|x - x_upper|, |x - x_lower|) <= 2*(1.5e-08*|x|+2.2e-16): true
 * Objective Function Calls: 8

а он подобрал Вам Метод Брента.
Или имея экспериментальные данные нужно оптимизировать коэффициенты модели


$F(p_1,p_2,x) = p_1\cos(p_2x) + p_2\sin(p_1x)$


$p_1 = 1, p_2 = 0.2$


F(p, x) = p[1]*cos(p[2]*x) + p[2]*sin(p[1]*x)

model(p) = sum( [ (F(p, xdata[i]) - ydata[i])^2 for i = 1:length(xdata)] )

xdata = [-2,-1.64,-1.33,-0.7,0,0.45,1.2,1.64,2.32,2.9]
ydata = [0.699369,0.700462,0.695354,1.03905,1.97389,2.41143,1.91091,0.919576,-0.730975,-1.42001]

res2 = optimize(model, [1.0, 0.2])

Results of Optimization Algorithm
 * Algorithm: Nelder-Mead
 * Starting Point: [1.0,0.2]
 * Minimizer: [1.8818299027162517,0.7002244825046421]
 * Minimum: 5.381270e-02
 * Iterations: 34
 * Convergence: true
   *  √(Σ(yᵢ-ȳ)²)/n < 1.0e-08: true
   * Reached Maximum Number of Iterations: false
 * Objective Calls: 71

P = Optim.minimizer(res2)
Y = [ F(P, x) for x in xdata]

using Plots
plotly()

plot(xdata, ydata)
plot!(xdata, Y)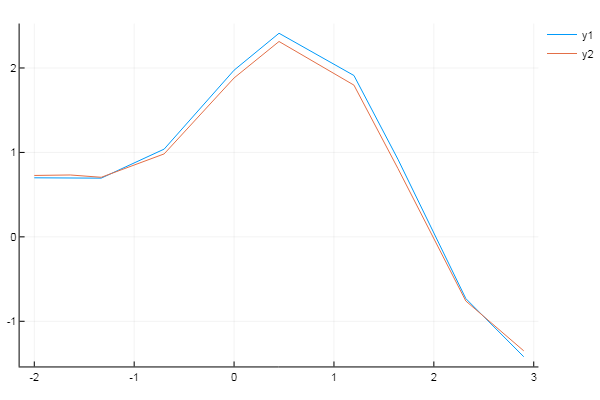


Бонус. Создание своей тестовой функции


Использована идея с хабровской статьи. Можно самому настроить каждый локальный минимум:


"""
https://habr.com/ru/post/349660/
    :param n: количество экстремумов
    :param a: список коэффициентов крутости экстремумов, чем выше значения, 
        тем быстрее функция убывает/возрастает и тем уже область экстремума
    :param c: список координат экстремумов
    :param p: список степеней гладкости в районе экстремума
    :param b: список значений функции
    :return: возвращает функцию, которой необходимо передавать одномерный список 
координат точки, возвращаемая функция вернет значение тестовой функции в данной точке
"""
function feldbaum(x; n=5, 
        a=[3 2; 4 3; 2 1; 4 5; .5 .5], 
        c=[-1 2; 2 1; -3 2; -2 -2; 1.5 -2], 
        p=[9 6; 1 1; 1.5 1.4; 1.2 1.3; 0.5 0.5], 
        b=[0 1 3.2 2 4.6])

    l = zeros(n)
    for i = 1:n
        res = 0
        for j = 1:size(x,1) 
            res += a[i,j] * abs(x[j] - c[i,j]) ^ p[i,j]
        end
        res += b[i]
        l[i] = res
    end
    minimum(l)
end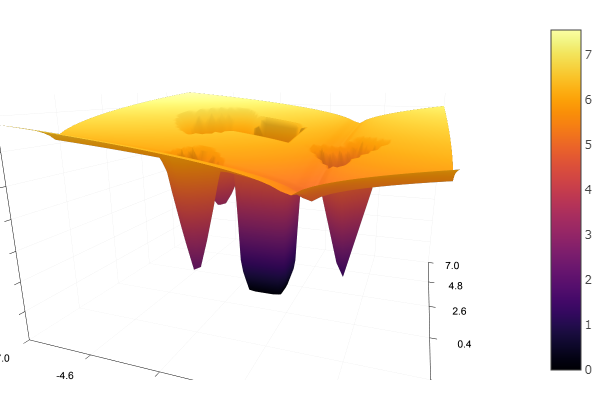



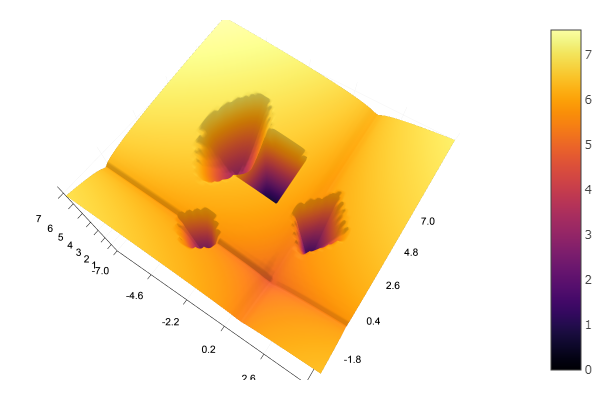
А можно всё предоставить воле всемогущего рандома


n=10
m = 2
a = rand(0:0.1:6, n, m)
c = rand(-2:0.1:2, n, m)
p = rand(0:0.1:2, n, m)
b = rand(0:0.1:8, n, m)

function feldbaum(x) 

    l = zeros(n)
    for i = 1:n
        res = 0
        for j = 1:m
            res += a[i,j] * abs(x[j] - c[i,j]) ^ p[i,j]
        end
        res += b[i]
        l[i] = res
    end
    minimum(l)
end


Но как видно из стартовой картинки рой частиц таким рельефом не запугаешь.


На этом следует закончить. Как можно убедиться Julia обладает довольно мощным и современным математическим окружением позволяющим проводить сложные численные исследования не опускаясь до низкоуровневых абстракций программирования. А это отличный повод продолжить изучение данного языка.


Всем удачной оптимизации!

Tags:
Hubs:
If this publication inspired you and you want to support the author, do not hesitate to click on the button
Total votes 17: ↑16 and ↓1+15
Comments3
237
Karma
0
Rating
Ермоленко Игорь @Yermack

Пользователь

Send message
VK

Articles

Your account

Sections

Information

Services

Support
© 2006–2024, Habr