В школьные годы у меня был одноклассник, который мог послушать, как работает машина во дворе, и с серьезным лицом вынести вердикт: все в порядке, или что-то сломалось, и нужно срочно бежать за новыми деталями/маслом/инструментами! Я, как абсолютный чайник в автомобильном деле, всегда слышал обычное дребезжание очередной двенашки, никаких отличий не замечая и просто молча поражаясь его слуху и скилам.
Сейчас разбираться во внутренностях автомобиля я лучше не стал, зато начал работать с обработкой звуковых сигналов и машинным обучением, и здесь мы с вами постараемся понять, а возможно ли научить компьютер улавливать в звуке работы двигателя отклонения от нормы?
Как минимум, это просто интересно проверить, а в перспект��ве такая технология могла бы сэкономить кучу денег автовладельцам. По крайней мере в моем представлении, под капотом критичные поломки происходят постепенно, и на ранних стадиях, многие из них можно услышать, быстро и дешево исправить, сэкономив время, деньги и без того шаткие нервы.
Ну что, пожалуй, пора перейти от слов к делу. Поехали!
Сразу хочу сказать, что во всем, что касается математики и алгоритмов, я буду делать больший упор на смысл и понимание, формул и математических выкладок здесь не будет. Никаких новых алгоритмов я здесь не разработал, за формулами, при желании, лучше обратиться к гуглу и википедии, а также воспользоваться ссылками, которые я буду оставлять на протяжении всей статьи.
Все объяснения я буду приводить на примере звука двигателя с поломкой, взятого из этого ролика на YouTube.
Скачанный с ютуба файл (можно скачать с помощью браузерных расширений или просто изменив в ссылке youtube на ssyoutube) конвертируем в wav формат с помощью ffmpeg:
ffmpeg -i input_video.mp4 -c:a pcm_s16le -ar 16000 -ac 1 engine_sound.wav
Прежде чем начать обработку этого файла, скажу пару слов о том, что такое спектрограмма, и как она пригодится нам при решении этой задачи. Многие из вас, наверняка, видели подобную картинку — это амплитудно-временное представление звука или осциллограмма.
Если простым языком, то звук — это волна, и на осциллограмме наблюдаются значения амплитуды этой волны в заданные моменты времени.
Чтобы получить из такого представления спектрограмму, нам потребуется преобразование Фурье. С его помощью можно получить амплитудно-частотное представление звука или амплитудный спектр. Такой спектр показывает, на какой частоте и с какой амплитудой выражен исследуемый сигнал.
По сути, спектрограмма — это набор спектров коротких последовательных кусочков сигнала. Пожалуй, такого "определения" нам будет достаточно, чтобы не отвлекаться сильно от задачи. Все станет понятнее, если посмотреть на визуализацию спектрограммы (картинка получена с помощью WaveAssistant). По оси X здесь отложено время, по оси Y — частота, то есть каждый столбец в этой матрице — это модуль спектра в заданный момент времени.
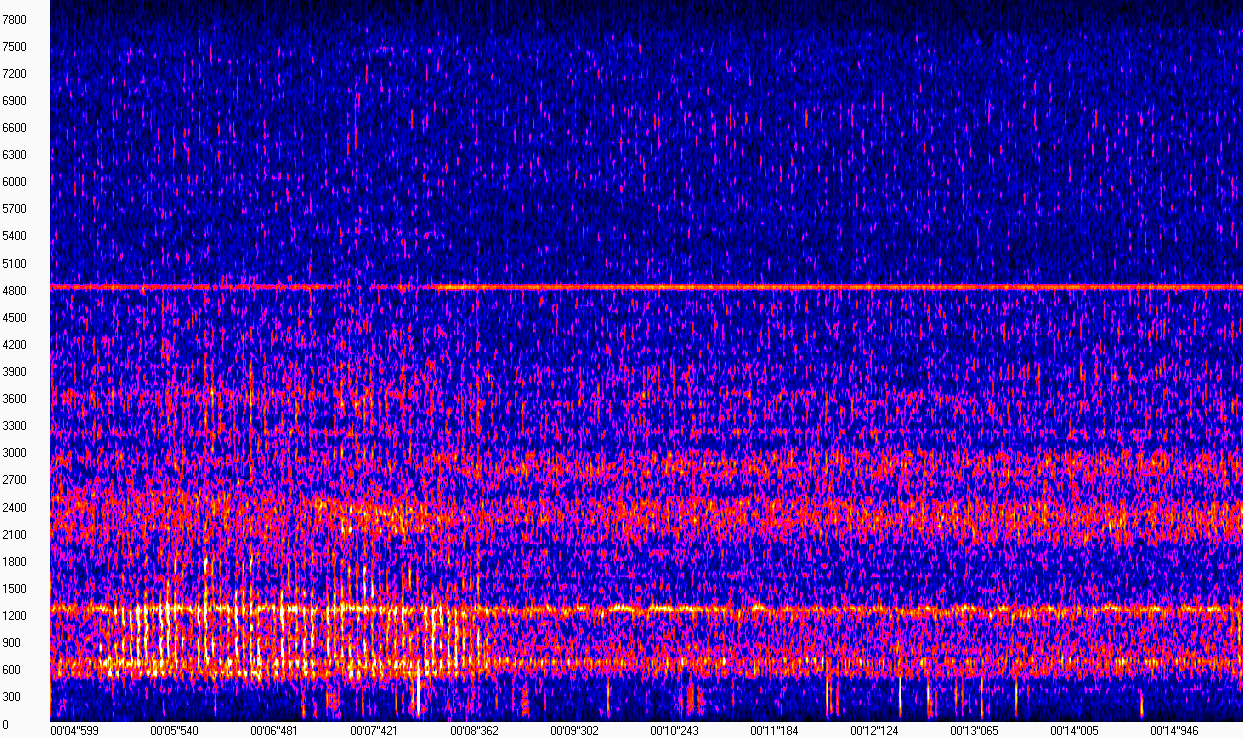
На этой спектрограмме видно, что звук двигателя при отсутствии постукивания "выглядит" примерно одинаково, и выражен на частотах в окрестности 600, 1200, 2400 и 4800 Гц. Звук стука, который беспокоит владельца, очень хорошо различим в диапазоне частот 600-1200 Гц с 5 по 8 секунду. Поскольку запись сделана в довольно шумных условиях на улице, на спектрограмме эти шумы также присутствуют, что несколько усложняет нашу задачу.
Тем не менее, глядя на такую спектрограмму, мы с уверенностью можем сказать, где стук был, а где его не было. У компьютера же глаз нет, поэтому нам нужно подобрать алгоритм, который будет способен различить подобное отклонение (а желательно и не только его) при условии наличия шумов в записи.
Рассчитать спектрограммы можно с помощью библиотеки librosa следующим образом:
from librosa.util import buf_to_float from librosa.core import stft # функция для вычисления спектрограммы import numpy as np from scipy.io import wavfile # для работы с wav-файлами def cut_wav(path_to_wav, start_time, end_time): sr, wav_data = wavfile.read(path_to_wav) return wav_data[int(sr * start_time): int(sr * end_time)] def get_stft(wav_data): feat = np.abs(stft(buf_to_float(wav_data), n_fft=fft_size, hop_length=fft_step)) # транспонирование - ставим ось времени на первое место return feat.T wav_path = './engine_sound.wav' train_features = [] # готовим признаки для обучения, time_list - содержит разметку данных for [ts, te] in time_list: wav_part = cut_wav(wav_path, ts, te) spec = get_stft(wav_part) train_features.append(spec) X_train = np.vstack(train_features) # готовим признаки для теста full_wav_data = wavfile.read(wav_path)[1] X_test = get_stft(full_wav_data)
Решение
Строго говоря, нам нужно решить задачу бинарной классификации, где нужно определить, сломан двигатель или работает в штатном режиме. Подобные задачи мы с коллегой уже описывали в своей предыдущей статье, там мы использовали сверточную нейронную сеть для классификации акустических событий. Здесь же такое решение вряд ли представляется возможным: нейронки очень любят, когда им даешь большие датасеты. Мы же имеем дело с одной вавкой длительностью чуть больше минуты, что большим датасетом явно не назовешь.
Выбор был остановлен на Gaussian Mixture Model (модель Гауссовых смесей). Хорошую статью, подробно описывающую принцип работы и обучения этой модели можно найти здесь Общая идея же этой модели заключается в том, чтобы описать данные с помощью сложного распределения в виде линейной комбинации нескольких многомерных нормальных распределений (подробнее о многомерном нормальном распределении здесь).
Так как двигатель в процессе своей работы звучит примерно "одинаково", звук его работы можно считать стационарным, и идея описания этого звука с помощью такого распределения выглядит вполне осмысленной. Чтобы понять суть GMM я очень рекомендую посмотреть пример обучения и выбора количества гауссоид здесь.
Наш случай отличается от представленных выше примеров тем, что вместо точек на двумерной плоскости буд��т использоваться значения спектра, взятые из спектрограммы сигнала. Подбирать параметры распределения, такие как тип ковариационной матрицы можно с помощью BIC критерия (пример, описание), однако в моем случае оптимальные с точки зрения этого критерия параметры показали себя хуже, чем те, что приведены в коде ниже:
from sklearn.mixture import GaussianMixture n_components = 3 gmm_clf = GaussianMixture(n_components) gmm_clf.fit(X_train)
Предполагая, что звук нормальной работы описывается распределением, параметры которого подобрались в процессе обучения, можно замерять, насколько любой звук "близок" к этому распределению.
Чтобы это сделать, можно вычислить среднее правдоподобие столбцов спектрограммы исследуемого сигнала, а затем подобрать порог, который будет отделять правдоподобие звуков хорошей работы от всех остальных. Построить правдоподобие для каждой секунды можно следующим образом:
n_seconds = len(full_wav_data) // sr gmm_scores = [] # правдоподобие на каждую секунду for i in range(n_seconds - 1): test_sec = X_test[(i * sr) // fft_step: ((i + 1) * sr) // fft_step, :] sc = gmm_clf.score(test_sec) gmm_scores.append(sc)
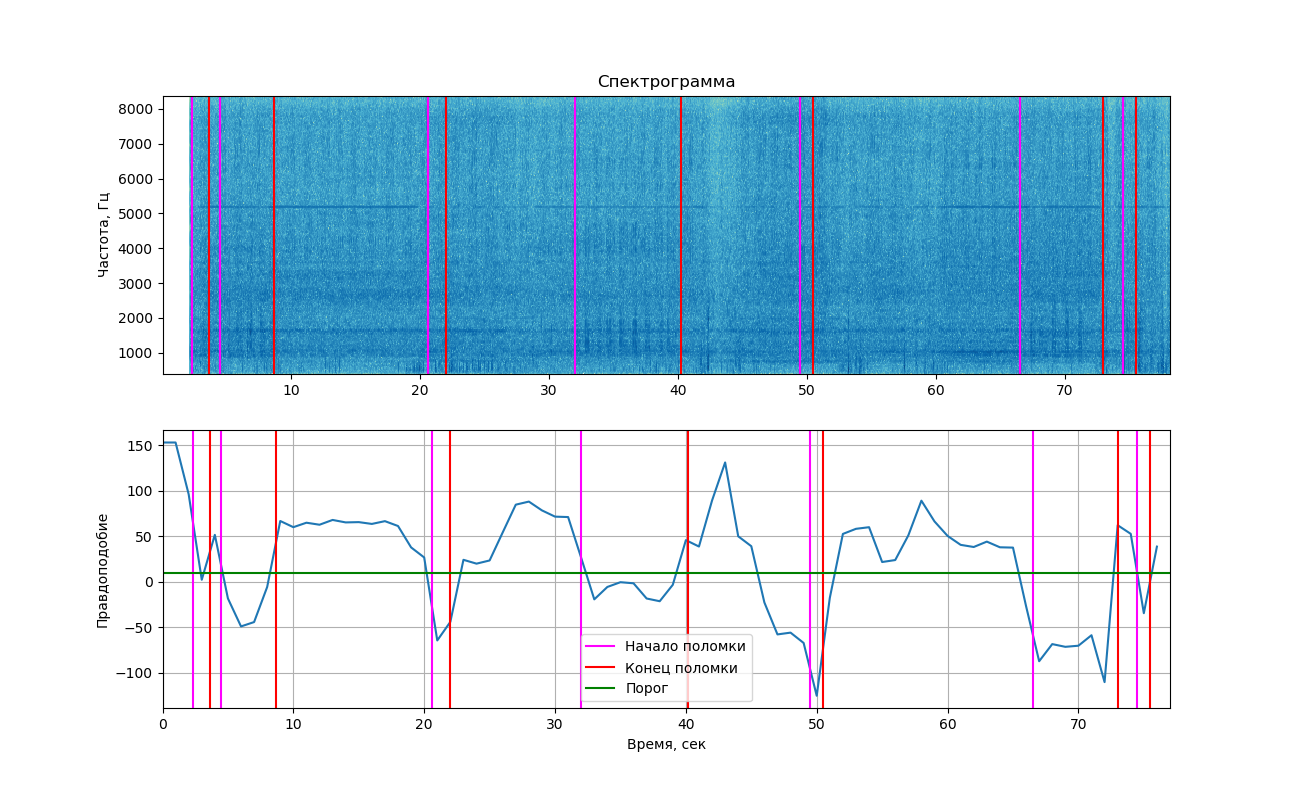
Если отобразить полученные правдоподобия на графике, то получим следующую картинку.
В верхней части изображена спектрограмма сигнала, отображенная с помощью библиотеки matplotlib. Изменения, вызванные стуком, на ней заметны не так сильно, как на примере выше (именно поэтому здесь вы увидели 2 изображения). Тем не менее, если приглядеться, их все равно можно разглядеть. Вертикальными линиями помечены времена начала и конца стуков.
Выводы
Как видно из графика, в моменты звучания стука правдоподобие действительно становилось ниже порога, а значит, мы бы смогли разделить два этих класса (работа со стуком и без него). Но нужно сказать, что это значение находится достаточно близко к пороговому и в участках, где стук не слышен. Это происходит потому, что в записи часто встречаются посторонние шумы, которые также влияют на величину правдоподобия.
Добавим сюда обучения на буквально нескольких секундах звука, плохие условия записи, и уже можно вообще удивляться тому, что эксперимент хоть как-то удался!
Скорее всего, чтобы этот способ применить на практике и быть уверенным в его надежности, звука придется записать куда больше, а также хорошо разместить микрофон, чтобы свести попадание шумов на записи к минимуму.
Эта статья — лишь попытка решить подобную задачу, не претендующая на абсолютную правильность, если у вас есть идеи и предложения, а может быть вопросы, давайте обсудим их вместе в комментах или лично.
Полный код на github — здесь