Часть третья, в которой Атос выпал в осадок, а Граф де ля Фер мудрит с алгоритмами.
UPD Часть первая здесь
UPD Часть вторая здесь
Вступление от авторов:
Добрый день! Сегодня мы продолжаем цикл статей, посвященных скорингу и использованию в оном теории графов. С первой и второй статьей Вы можете познакомиться соответственно здесь и здесь. Настоятельно рекомендуем, иначе, данная статья может показаться бессмысленным экспериментом с алгоритмами.
Все шуточные аллегории, вставки и прочее, призваны немного разгрузить повествование и не позволить ему свалиться в нудную лекцию. Всем, кому не зайдет наш юмор, заранее приносим извинения
Цель данной статьи: не более, чем за 30 минут, описать алгоритм построения графа и рассчитать скоринговый балл для НПАО «Один за всех».
Термины и определения:
- Алгоритм поиска в глубину (DFS, Depth-first search) — Стратегия поиска в глубину, как и следует из названия, состоит в том, чтобы идти «вглубь» графа, насколько это возможно. Алгоритм поиска описывается рекурсивно: перебираем все исходящие из рассматриваемой вершины рёбра. Если ребро ведёт в вершину, которая не была рассмотрена ранее, то запускаем алгоритм от этой нерассмотренной вершины, а после возвращаемся и продолжаем перебирать рёбра. Возврат происходит в том случае, если в рассматриваемой вершине не осталось рёбер, которые ведут в нерассмотренную вершину. Если после завершения алгоритма не все вершины были рассмотрены, то необходимо запустить алгоритм от одной из нерассмотренных вершин
- Рекурсия — вызов функции (процедуры) из неё же самой, непосредственно (простая рекурсия) или через другие функции (сложная или косвенная рекурсия)
В первой нашей статье (здесь) мы определили модель графа, с которой будем экспериментировать, и дали ей краткую характеристику.
Во второй нашей статье (здесь) мы описали основные структуры данных, которые можно использовать для хранения графа и чуть более подробно описали модель графа и способ работы с ней.
Пришло время вытащить шпагу из ножен и начать уже всех колоть, точнее, создать алгоритм расчета скорингового балла для НПАО «Один за всех».
Погнали!
Алгоритм будет выполнен на языке Python. Как говорится, натянем змею на шпагу!
Граф будет храниться в словаре, в следующем виде:
graph = {
'Odin_za_vseh' : {'goody': 10, 'rank': 4, 'fund':4, 'relations':{'Bonasye':3, 'Trevi': 1, 'Gusak':2,'Suchka':5, 'Roshfor':1, 'Cardi':1}},
'Cardi' : {'goody': -8, 'rank': 9, 'fund':8, 'relations':{'Korol':2,'Odin_za_vseh':3,'Gvardia':5, 'Roshfor':5 }},
'Roshfor' : {'goody': -7, 'rank': 7, 'fund':5,'relations':{'Cardi':1, 'Suchka': 3,'Odin_za_vseh':2, 'Bonasye':5 }},
'Suchka' : {'goody': -10, 'rank': 4, 'fund':4, 'relations':{'Odin_za_vseh':5,'Roshfor':3 }},
'Gvardia' : {'goody': -5, 'rank': 3, 'fund':4, 'relations':{'Cardi':1,'Gusak':1 }},
'Gusak' : {'goody': -7, 'rank': 4, 'fund':4, 'relations':{'Gvardia':5,'Odin_za_vseh':2 }},
'Trevi' : {'goody': 7, 'rank': 5, 'fund':5, 'relations':{'Odin_za_vseh':4,'Mushketery':5 }},
'Bonasye': {'goody': -2, 'rank': 2, 'fund':3, 'relations':{'Odin_za_vseh':1,'Roshfor':1,'Konsta':2 }},
'Konsta' : {'goody': 10, 'rank': 5, 'fund':3, 'relations':{'Koroleva':2,'Bonasye':1 }},
'Mushketery' : {'goody': 7, 'rank': 5, 'fund':4, 'relations':{'Korol':1, 'Trevi':1}},
'Koroleva' : {'goody': 6, 'rank': 8, 'fund':7, 'relations':{'Korol':2,'Konsta':5, 'EnglishMan':3 }},
'Korol' : {'goody': 5, 'rank': 10, 'fund':10, 'relations':{'Cardi':3, 'Koroleva':5,'Mushketery':5 }},
'EnglishMan' : {'goody': 5, 'rank': 8, 'fund':10, 'relations':{'Koroleva':2}}
}'goody' – оценка узла – хороший или плохой и степень «главности» узла. Например, Кардинал является отрицательным героем фильма, поэтому его оценка с минусом. Кардинал является одним из ключевых врагов наших героев, но не самым главным (мы так решили)
'rank' – оценка узла в табели о рангах
'fund' – состоятельность узла
'relations' – с кем связан и насколько может влиять на связанный с ним узел
Пока все просто, но внимательный читатель уже мог заметить некоторые особенности, да, и без того возникают вопросы по содержанию. Попробуем их предугадать и ответить. Право первого укола за нами!
Думаю, не стоит объяснять, что мы использовали для названия ключа словаря первого уровня. Вы уже прекрасно догадались, хотя, некоторые имена и подверглись изменениям, обусловленным нашим восприятием произведения.
Откуда взялись эти параметры ('goody', 'rank' и т.д.), почему именно они и откуда появилась их оценка?
По порядку:
- В реальной жизни эти параметры будут характеризовать конкретный узел-компанию. Для каждого, кто будет проводить оценку и в зависимости от типа этой оценки, эти параметры будут отличаться. Например, такими параметрами для оценки скоринга заемщика могут быть – оборот, величина кредиторской/дебиторской задолженности, исполнительные листы и т.д.
- Почему именно они – автор так видит))) данные параметры отражают суть того, что описывает Граф, на наш взгляд
- Оценка является, как это принято сейчас говорить, экспертной. В реальной жизни эта оценка будет получаться с помощью майнинга. Более подробно об этом мы будем писать в следующей статье.
Почему у некоторых узлов разная величина обоюдной связи (например, Odin_za_vseh — Bonasye = 3, а Bonasye — Odin_za_vseh = 1)? Происходит это потому, что Odin_za_vseh оказывает на Bonasye гораздо большее влияние, чем наоборот. И это важно понимать. При скоринге Odin_za_vseh нам необходимо будет учитывать влияние именно Bonasye на Odin_za_vseh.
Что такое оценка связи и как она рассчитывается?
- Оценка связи – это мера влияния одного узла на другой
- Каждая связь в нашем Графе является двусторонней, но при этом оценка связи в разных направлениях может различаться
- Оценка связи – это величина от 1 до 5 (от 1 до 5 просто для примера). Отрицательной связь быть не может, т.к. узел либо связан с другим, и мы оцениваем, насколько он влияет на этот узел, либо не связан. При этом, конечно, связь с неблагонадежным узлом, в конечном итоге, будет отрицательной для узла, который мы оцениваем, т.к. этот неблагонадежный узел будет иметь отрицательную внутреннюю оценку.
- Внутренняя оценка узла – агрегированная величина, складывающаяся из внутренних параметров узла. В нашем примере – это 'goody', 'rank', 'fund'. Внутренняя оценка может быть отрицательной.
Как будет считаться скоринговый бал?
- Каждая компания, которая будет использовать этот подход, может закладывать свой расчет скорингового балла, опираясь на свои требования и свой опыт хозяйственной деятельности
- В нашем случае, мы выбрали простой и не затейливый способ:
- Скоринговый балл = Внутренний балл узла, который мы оцениваем + Сумма (Внутренняя оценка дочернего узла 1 уровняоценку влияния этого узла на оцениваемый узел) + (Сумма(Внутренняя оценка дочернего узла 2 уровняоценку влияния этого узла на родительский узел 1 уровня)/2)
- Если получается отрицательный скоринговый балл, то кредит не даем
- Представленный далее алгоритм является базовым и может быть легко видоизменен, под любую методику расчета скорингового балла
- Вся сложность будет в «правильном» майнинге, но он будет описан уже в следующей статье
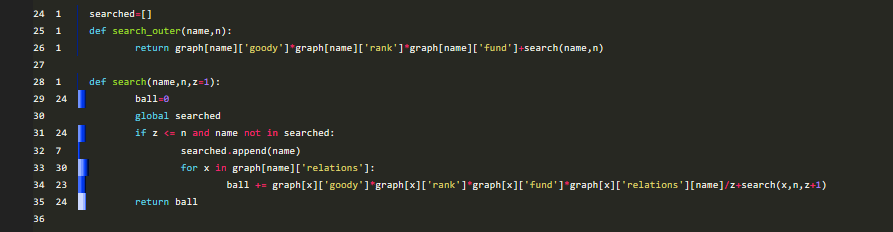
А вот и сам алгоритм:
searched=[] #Список проверенных узлов
def search_outer(name,n):
return graph[name]['goody']*graph[name]['rank']*graph[name]['fund']+search(name,n)
#Метод search_outer() создан исключительно для того, чтобы прибавить внутреннюю оценку узла к #баллу, который будет рассчитан рекурсивно в методе search()
#name – это имя узла, для которого производится скоринг
#n – глубина расчета – сколько уровней дочерних узлов мы обходим
def search(name, n, z=1):
ball=0 #Переменная, которая будет хранить скоринговый бал
global searched #Обращение к глобальной переменной
if z <= n and name not in searched: #Проверка уровня и наличия узла в списке проверенных
searched.append(name)
for x in graph[name]['relations']: #Перебираем связи узла
ball += graph[x]['goody'] * graph[x]['rank'] * graph[x]['fund'] * graph[x]['relations'][name] / z + search(x,n,z+1) #Рассчитываем балл и рекурсивно вызываем этот #метод для каждого узла, по которому считаем балл
return ball
#Тут, думаю, все понятно и стандартно
def main():
ball = search_outer ('Odin_za_vseh', 2)
print(ball)
if __name__ == '__main__':
main()
Подводим итог:
- Уверен, что прочтение статьи не заняло более 30 минут
- Скоринговый балл для НПАО «Один за всех» мы рассчитали. Кредит не даем, НПАО «Один за всех» оказались те еще авантюристы, с кучей врагов. Кредит можем дать бюджетникам, например, 'Mushketery'
- Алгоритм получился несложный и достаточно эффективный
- Вычислительная сложность равна O(N**d+1), где d — это количество уровней. Визуально работа алгоритма отображена на рисунке ниже
Можно переходить к самому интересному и сложному – майнингу данных!
P.S. Касаемо ссылок на другие статьи с теорией (в прошлой статье нам сделали замечание):