Задача 1.3
Задача 1.4
Задача 1.5
Задача 1.6
Задача 1.7
Планиметрия изучается в начальном курсе геометрии и зачастую сводится к решению практических задач без изучения теоретической базы.
В данной статье приводятся некоторые решения задач первого раздела приложения Euclidea (геометрические построения с помощью циркуля и линейки).
Решения задач 1.1, 1.2 и 1.3 основаны на том, что с помощью циркуля и линейки можно построить равносторонний треугольник.
Рассмотрим Предложение I, приведённое в «Началах» Евклида
Такой треугольник строится на пересечении двух окружностей одного диаметра.
Доказательство того, что этот треугольник равносторонний приводится далее в Предложении I «Начал»

Постройте точку, делящую отрезок на две равные части.
Эту задачу можно решить, используя построения из предыдущей задачи, но здесь я буду использовать построения одним только циркулем
и построение одной только линейкой
Постройте окружность, вписанную в квадрат.
Общими точками у квадрата и вписанной в него окружности будут середины рёбер квадрата. Середину ребра можно найти, опустив на него перпендикуляр из точки пересечения диагоналей квадрата.
Для того, чтобы построить такой перпендикуляр, решим вспомогательную задачу
2.6 Опустить перпендикуляр
Эта задача есть в книге «Занимательная геометрия»
Вернёмся к задаче 1.4
Опустим перпендикуляр из точки пересечения диагоналей квадрата на одну из его сторон.
Для этого построим окружность с центром, принадлежащим нижнему (горизонтальному) ребру квадрата.
И опустив перпендикуляр из точки пересечения диагоналей квадрата на ребро, найдём середину ребра.
Это же построение можно использовать для решения задачи 2.9 Окружность, касающаяся прямой
Задачу 1.5 можно решить по теореме Предложения I «Начал» Евклида, приведённой в начале статьи.
Центр окружности можно найти, построив диаметр этой окружности и разделив его пополам; для построения диаметра можно воспользоваться, например, теоремой Фалеса об угле, опирающемся на диаметр окружности

Построим две хорды, лежащие под прямым углом друг к другу; соединим противоположные концы хорд

Соответственно, центром окружности будет являться точка, лежащая посередине построенного диаметра, т.е. точка, которая делит диаметр пополам.
Эти же построения можно использовать для решения задачи 2.7
Определение: касательной к окружности называется прямая, имеющая с окружностью одну общую точку. Касательная к окружности перпендикулярна радиусу, проведённому в точку касания.
Рассмотрим задачу 2.8
2.8 Касательная к окружности в точке
Возвращаясь к предыдущей задаче, эту задачу можно решить построив угол, опирающийся на диаметр окружности по теореме Фалеса

Да, задача навскидку решается за 4Е действия

Далее, построив перпендикуляр к касательной, найдём диаметр окружности, и, разделив его пополам, найдём центр окружности.
Ещё об одном способе построения касательной к окружности можно узнать из лекции 1.5 курса «Геометрия и группы» А. Савватеева ссылка
В книге «Занимательная геометрия» рассматривается аналогичная этой задаче

Решим задачу методом Мора-Маскерони.
Построим три окружности радиусом r и две окружности радиусом

В приложении нет такой операции, как перенос раствора циркуля (равного MO), поэтому необходимо использовать дополнительные построения.
Для того, чтобы построить касательную к исходной окружности, параллельную МО, необходимо произвести построения, которые были приведены выше (построить три окружности радиусом r и две окружности радиусом ), но вместо исходной окружности взять окружность, обозначенную на рисунке синим цветом
), но вместо исходной окружности взять окружность, обозначенную на рисунке синим цветом

Т.о. мы перенесли раствор циркуля (равный МО) в точку А.
Далее из точки А необходимо провести окружность c радиусом МО

P.S. Ксати, у создателей приложения есть своя группа в VK vk.com/euclidea
Задача 1.4
Задача 1.5
Задача 1.6
Задача 1.7
Планиметрия изучается в начальном курсе геометрии и зачастую сводится к решению практических задач без изучения теоретической базы.
В данной статье приводятся некоторые решения задач первого раздела приложения Euclidea (геометрические построения с помощью циркуля и линейки).
Решения задач 1.1, 1.2 и 1.3 основаны на том, что с помощью циркуля и линейки можно построить равносторонний треугольник.
1.1 Построить угол 60° с заданой стороной
1.2 Построить серединный перпендикуляр к отрезку
Рассмотрим Предложение I, приведённое в «Началах» Евклида
На данной ограниченной прямой построить равносторонний треугольник
Такой треугольник строится на пересечении двух окружностей одного диаметра.
Доказательство того, что этот треугольник равносторонний приводится далее в Предложении I «Начал»

1.3 Середина отрезка
Постройте точку, делящую отрезок на две равные части.
Эту задачу можно решить, используя построения из предыдущей задачи, но здесь я буду использовать построения одним только циркулем
Построение одним только циркулем
Итак, теорема Мора-Маскерони гласит, что
Рассмотрим сперва задачу 4.1 Удвоенный отрезок
В книге Я. Перельмана «Занимательная геометрия» приводится решение этой задачи
Далее необходимо построить равнобедренный треугольник с основанием, равным r и длинами боковых сторон, равными 2r.

AEF — равнобедренный треугольник с основанием, равным r и длинами боковых сторон, равными 2r.
AFM — равнобедренный треугольник с основанием, равным r/2 и длинами боковых сторон, равными r.
Ссылка на источник
всё, что можно построить с помощью циркуля и линейки, может быть построено с помощью одного циркуля.
Рассмотрим сперва задачу 4.1 Удвоенный отрезок
В книге Я. Перельмана «Занимательная геометрия» приводится решение этой задачи
Из точки В радиусом АВ описываем окружность.
По этой окружности откладываем от точки А расстояние АВ три раза: получаем точку С, очевидно, диаметрально противоположную А. Расстояние АС представляет собой двойное рассрастояние АВ. Проведя окружность из С радиусом ВС, мы можем таким же образом найти точку,
диаметрально противоположную В и, следовательно, удаленную от А на
тройное расстояние АВ, и т. д.
Далее необходимо построить равнобедренный треугольник с основанием, равным r и длинами боковых сторон, равными 2r.

AEF — равнобедренный треугольник с основанием, равным r и длинами боковых сторон, равными 2r.
AFM — равнобедренный треугольник с основанием, равным r/2 и длинами боковых сторон, равными r.
Ссылка на источник
и построение одной только линейкой
Построение одной только линейкой
Итак, по теореме Штейнера — Понселе:
Решим вспомогательную задачу:
Провести прямую, параллельную данному отрезку.

Далее в приложении есть похожая задача 5.1 Параллельная прямая через точку.
Поскольку треугольник, образованый пересечением диаметров и прямой, является равнобедренным; и поскольку углы при основании треугольника равны, то и вписанные углы, образованые пересечением диаметров и прямой равны, а значит данные прямые параллельны.
Далее, решим Задачу 1 из параграфа 3 книги «Геометрические построения на плоскости» (Б.И. Аргунов, М.Б. Балк.)
Задача 1: Даны две параллельные прямые а и b и на одной из них, например a, отрезок AB. Построить середину этого отрезка.
Для решения нам понадобится одно вспомогательное предложение («лемма о трапеции»):
Прямая, соединяющая точку пересечения диагоналей трапеции с точкой пересечения продолженных её боковых сторон, делит оба основания трапеции пополам.
Далее в книге приводится доказательство, которое я приводить не буду
Решение:
Изберем произвольную точку P, лежащую вне полосы, ограниченной заданными прямыми

Проведем прямые PA и PB и отметим точки D и C их пересечения прямой b. Пусть О — точка пересечения прямых AC и BD. Тогда, согласно предыдущей лемме, прямая PO пересечёт отрезок AB в его середине M.
Решением задачи 1.3 по методу Штейнера-Понеселе будет:

любое построение, выполнимое на плоскости циркулем и линейкой, можно выполнить одной линейкой, если нарисована хотя бы одна окружность и отмечен её центр.
Решим вспомогательную задачу:
Провести прямую, параллельную данному отрезку.

Далее в приложении есть похожая задача 5.1 Параллельная прямая через точку.
Поскольку треугольник, образованый пересечением диаметров и прямой, является равнобедренным; и поскольку углы при основании треугольника равны, то и вписанные углы, образованые пересечением диаметров и прямой равны, а значит данные прямые параллельны.
Далее, решим Задачу 1 из параграфа 3 книги «Геометрические построения на плоскости» (Б.И. Аргунов, М.Б. Балк.)
Задача 1: Даны две параллельные прямые а и b и на одной из них, например a, отрезок AB. Построить середину этого отрезка.
Для решения нам понадобится одно вспомогательное предложение («лемма о трапеции»):
Прямая, соединяющая точку пересечения диагоналей трапеции с точкой пересечения продолженных её боковых сторон, делит оба основания трапеции пополам.
Далее в книге приводится доказательство, которое я приводить не буду
Решение:
Изберем произвольную точку P, лежащую вне полосы, ограниченной заданными прямыми

Проведем прямые PA и PB и отметим точки D и C их пересечения прямой b. Пусть О — точка пересечения прямых AC и BD. Тогда, согласно предыдущей лемме, прямая PO пересечёт отрезок AB в его середине M.
Решением задачи 1.3 по методу Штейнера-Понеселе будет:

1.4 Окружность, вписанная в квадрат
Постройте окружность, вписанную в квадрат.
Общими точками у квадрата и вписанной в него окружности будут середины рёбер квадрата. Середину ребра можно найти, опустив на него перпендикуляр из точки пересечения диагоналей квадрата.
Для того, чтобы построить такой перпендикуляр, решим вспомогательную задачу
2.6 Опустить перпендикуляр
Эта задача есть в книге «Занимательная геометрия»
Из точки A, лежащей вне данной полуокружности, опустить на её диаметр перпендикуляр, обходясь при этом без циркуля. Положение центра полуокружности не указано.
Нам пригодится здесь то свойство треугольника, что все его высоты пересекаются в одной точке. Соединим A с B и C; получим точки D и E. Прямые BE и CD, очевидно, — высоты треугольника ABC. Третья высота — искомый перпендикуляр к BC — должна проходить через пересечение двух других, т.е. через точку M. Проведя по линейке прямую через точки A и M, мы выполним требованиек задачи, не прибегая к услугам циркуля.
Вернёмся к задаче 1.4
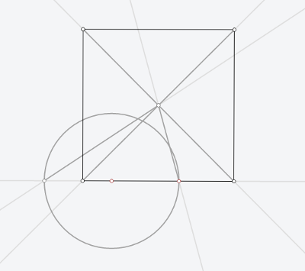
Опустим перпендикуляр из точки пересечения диагоналей квадрата на одну из его сторон.
Для этого построим окружность с центром, принадлежащим нижнему (горизонтальному) ребру квадрата.

И опустив перпендикуляр из точки пересечения диагоналей квадрата на ребро, найдём середину ребра.
Это же построение можно использовать для решения задачи 2.9 Окружность, касающаяся прямой
1.5 Ромб, вписанный в прямоугольник
Задачу 1.5 можно решить по теореме Предложения I «Начал» Евклида, приведённой в начале статьи.
1.6 Найти центр окружности
Центр окружности можно найти, построив диаметр этой окружности и разделив его пополам; для построения диаметра можно воспользоваться, например, теоремой Фалеса об угле, опирающемся на диаметр окружности
Плоский угол, опирающийся на диаметр окружности, — прямой.

Построим две хорды, лежащие под прямым углом друг к другу; соединим противоположные концы хорд

Соответственно, центром окружности будет являться точка, лежащая посередине построенного диаметра, т.е. точка, которая делит диаметр пополам.
Эти же построения можно использовать для решения задачи 2.7
2.7 Восстановить перпендикуляр
Построим произвольную окружность, проходящую через точку, из которой необходимо восстановить перпендикуляр.

По теореме Фалеса угол, опирающийся на диаметр, является прямым, а искомым перпендикуляром является хорда, соединяющая точку, из которой необходимо восстановить перпендикуляр, с точкой пересечения диаметра с окружностью.
Ксати, задачу 2.7 можно решить, например, так

Эту задачу можно решить с помощью одного циркуля, разделив дугу верхней полуокружности пополам, построив окружность из этой точки, а затем найти точку пересечения прямой и окружности.
Это построение можно использовать и для решения задачи 3.5


По теореме Фалеса угол, опирающийся на диаметр, является прямым, а искомым перпендикуляром является хорда, соединяющая точку, из которой необходимо восстановить перпендикуляр, с точкой пересечения диаметра с окружностью.
Ксати, задачу 2.7 можно решить, например, так

Эту задачу можно решить с помощью одного циркуля, разделив дугу верхней полуокружности пополам, построив окружность из этой точки, а затем найти точку пересечения прямой и окружности.
Это построение можно использовать и для решения задачи 3.5

Определение: касательной к окружности называется прямая, имеющая с окружностью одну общую точку. Касательная к окружности перпендикулярна радиусу, проведённому в точку касания.
Рассмотрим задачу 2.8
2.8 Касательная к окружности в точке
Возвращаясь к предыдущей задаче, эту задачу можно решить построив угол, опирающийся на диаметр окружности по теореме Фалеса

Да, задача навскидку решается за 4Е действия

Доказательство
Докажем, что оранжевая прямая действительно является касательной к исходной окружности. Как показано в Предложении I «Начал», треугольник, построенный на пересечении двух окружностей является равносторонним.
Рассмотрим равносторонний треугольник с длиной ребра, равной 2r и вершиной, лежащей в центре исходной окружности. Тогда касательной к окружности будет одна из биссектрис/медиан/высот треугольника.

Можно замеить, что оранжевая линия лежит в основании равнобедренного треугольника

Оказывается, такой треугольник можно построить без привязки к центру окружности

Вообще, данные построения можно сделать без использования вспомогательных прямых, а значит эта задача решается в 3Е действия.
Рассмотрим равносторонний треугольник с длиной ребра, равной 2r и вершиной, лежащей в центре исходной окружности. Тогда касательной к окружности будет одна из биссектрис/медиан/высот треугольника.

Можно замеить, что оранжевая линия лежит в основании равнобедренного треугольника

Оказывается, такой треугольник можно построить без привязки к центру окружности

Вообще, данные построения можно сделать без использования вспомогательных прямых, а значит эта задача решается в 3Е действия.
Далее, построив перпендикуляр к касательной, найдём диаметр окружности, и, разделив его пополам, найдём центр окружности.
Ещё об одном способе построения касательной к окружности можно узнать из лекции 1.5 курса «Геометрия и группы» А. Савватеева ссылка
1.7 Квадрат, вписанный в окружность
В книге «Занимательная геометрия» рассматривается аналогичная этой задаче
Задача Наполеона

Решим задачу методом Мора-Маскерони.
Построим три окружности радиусом r и две окружности радиусом

В приложении нет такой операции, как перенос раствора циркуля (равного MO), поэтому необходимо использовать дополнительные построения.
Для того, чтобы построить касательную к исходной окружности, параллельную МО, необходимо произвести построения, которые были приведены выше (построить три окружности радиусом r и две окружности радиусом

Т.о. мы перенесли раствор циркуля (равный МО) в точку А.
Далее из точки А необходимо провести окружность c радиусом МО

P.S. Ксати, у создателей приложения есть своя группа в VK vk.com/euclidea

