Постквантовый блокчейн

Введение

В последние несколько лет большую популярность обретают системы, в основе которых лежит так называемый блокчейн, привлекающий пользователей рядом своих преимуществ: децентрализацией, неизменяемостью данных, прозрачностью, а также отсутствием доверенного центра, то есть посредника. Предоставление таких преимуществ возможно благодаря двум “китам” блокчейна: асимметричному шифрованию и использованию хэш-функций. Однако в связи с развитием квантовых вычислений безопасность этих примитивов стала под угрозой, поэтому возникает необходимость нахождения новых подходов к построению блокчейна, который будет устойчив к атакам с помощью квантового компьютера — так называемого постквантового блокчейна. В данной статье освещается, какие части блокчейна являются наиболее уязвимыми для атак с помощью квантового компьютера, насколько реальны эти угрозы, какие существуют подходы к построению постквантового блокчейна, устойчивого к ним, и насколько применимыми оказываются эти подходы.

Устройство блокчейна

Для начала вспомним, что из себя представляет блокчейн, чтобы затем понять, почему он уязвим к атакам с помощью квантового компьютера. По сути, блокчейн — это база данных, состоящая из цепочки блоков, в которой каждый блок хранит в себе хэш от предыдущего блока, в результате чего для изменения или удаления блока из середины цепочки необходимо перестраивать все последующие блоки. Подсчет каждого блока является вычислительно сложной задачей, поэтому перерасчет блоков оказывается практически невозможным и поэтому блокчейн обладает свойством неизменяемостью данных.

Такой вычислительно сложной задачей может быть, например, поиск коллизий хэша: нахождение некоего числа, proof-of-work (англ.: доказательство работы), при добавлении которого хэш от блока начинается с нескольких нулей. Данная задача с помощью классического компьютера может решаться лишь перебором, из-за чего среднее время нахождения такого числа экспоненциально растет с ростом требуемого количества нулей. Более подробно об этом можно прочитать в оригинальной статье С. Накамото, предложившего данную идею.

Блоки состоят из сформированных пользователями транзакций, которые подписываются ими с использованием асимметричной криптографии. Каждый пользователь имеет два ключа: приватный, известный только этому пользователю, с помощью которого он подписывает транзакции, и публичный, известный всем пользователям, с помощью которого кто угодно может проверить подпись. Например, биткоин использует для подписи транзакций алгоритм ECDSA (англ.: Elliptic Curve Digital Signature Algorithm), схожий с алгоритмом DSA (англ.: Digital Signature Algorithm), но определенный в группе точек эллиптической кривой. Криптографическая стойкость данного алгоритма основывается на сложности задачи дискретного логарифмирования, которая на классическом компьютере решается за экспоненциальное время относительно размера ключа. Другой вычислительно сложной задачей является задача факторизации больших чисел, на которой, например, основан алгоритм RSA (англ.: Rivest Shamir Adleman), также обеспечивающий криптографическую стойкость цифровой подписи, поскольку лежащая в основе него задача решается за время, которое экспоненциально зависит от размера ключа. Таким образом, пока эта криптографическая стойкость существует, пользователям гарантируется, что никто другой не сможет сгенерировать транзакции от их имени.

Уязвимость перед квантовым компьютером

Как было сказано выше, блокчейн опирается на две вычислительно сложные задачи: поиск коллизий хэша и взятие дискретного логарифма или факторизацию больших чисел. Обе задачи решаются на классическом компьютере за экспоненциальное время, благодаря чему при выборе достаточно сложной хэш-функции или достаточно длинного ключа могут считаться нерешаемыми. Однако настоящим потрясением оказалось то, что существуют алгоритмы, благодаря которым квантовые компьютеры способны решать эти задачи на порядки быстрее.

В то время как классический компьютер оперирует с битами, которые представляются в виде нуля или единицы, квантовый компьютер оперирует с кубитами, которые могут пребывать в суперпозиции различных состояний. Говоря упрощенно, каждое такое состояние может обрабатываться одновременно, в результате чего возможно получить существенное ускорение по сравнению с классическим аналогом. Далее рассматриваются два основных квантовых алгоритма, способных поставить под угрозу безопасность привычного блокчейна.

Алгоритм Гровера

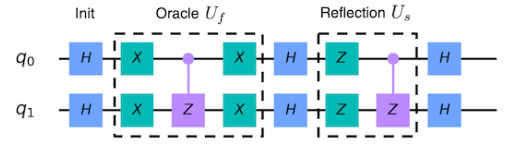
Алгоритм Гровера позволяет получать квадратичное ускорение в решении задачи перебора, поэтому может быть использован для ускорения генерации хэшей. Благодаря этому злоумышленник сможет генерировать ложные блоки на порядки быстрее генерации настоящих блоков, тем самым создавая более длинную цепочку блоков, которая будет принята всеми пользователями. Также этот алгоритм может быть использован для замены уже существующих блоков в блокчейне, при этом сохраняя их целостность.

Суть алгоритма Гровера заключается в следующем. Допустим, мы имеем некую функцию , корень которой мы собираемся найти. Пусть эта функция реализуема на классическом компьютере, тогда в теории представляется возможным реализовать обратимую функцию , которая равняется , если является корнем функции , и — в противном случае. Такая функция называется оракулом, а её обратимость обеспечивает то, что её можно реализовать на квантовом компьютере, например, при помощи вентилей Тоффоли. В таком случае на вход этой функции можно подавать не одно значение , как в классическом переборе, а суперпозицию всех возможных значений , а значит, получать на выходе суперпозицию всех возможных выходных значений оракула. Далее с помощью элементарных квантовых вентилей можно усилить амплитуду вероятности состояния, соответствующего корню оракула. После определенного количества таких итераций в результате измерения будет получен корень исходной функции с вероятностью, практически равной . Ситуация несколько осложняется в случае, когда у функции имеется несколько корней, что соответствует задаче поиска коллизий хэша, однако и в таком случае алгоритм Гровера показывает значительное ускорение по сравнению с простым перебором.

Атака на proof-of-work

Несмотря на то, что алгоритм Гровера способен обеспечить квадратичное ускорение при подсчете блоков, атака с его помощью не является для блокчейна критической, что утверждается в недавнем отчете группы канадских и австралийских ученых. Дело в том, вычислительная мощность интегральных схем специального назначения (англ.: ASIC), находящаяся в настоящий момент в руках майнеров, способна свести на нет практически любые попытки получить ускорение майнинга при помощи квантового компьютера. Допускается, однако, что дальнейшее развитие квантовых технологий может способствовать тому, что квантовые компьютеры получат серьезное преимущество над существующими вычислительными мощностями, но это, по оценкам авторов работы, наступит лишь после повсеместного распространения квантовых компьютеров. Когда же это настанет, майнеры также получат возможность использовать их, тем самым возможность доминирования с помощью квантового компьютера снизойдет на нет.

Кроме того, существуют и другие подходы к генерации блоков, в основе которых не лежат вычислительно сложные задачи, а значит, блокчейны на их основе могут рассматриваться как устойчивые к атакам на proof-of-work. Наиболее популярным таким подходом, который в настоящий момент уже используется, например, в BlackCoin, является proof-of-stake (англ.: доказательство доли владения), заключающийся в том, что блоки с большей вероятностью генерируются теми пользователями, которые владеют большей частью средств в блокчейне. Proof-of-stake не требует поиска коллизий хэша, поэтому с этой точки зрения является устойчивой к атакам с помощью квантового компьютера.

Однако proof-of-stake по-прежнему уязвим к атакам с помощью квантового компьютера, если он способен подделывать цифровые подписи, например, используя алгоритм Шора, рассматриваемый далее. В таком случае злоумышленник сможет очень быстро сосредоточить все средства блокчейна на подконтрольных счетах и получить полный контроль над ним. Стоит отметить, что цифровые подписи широко распространены и в других областях, которые теперь могут стать уязвимыми для квантового компьютера, из-за чего ведутся активные исследования по разработке новых подходов к созданию цифровых подписей, ряд которых будет рассмотрен в данной статье в дальнейшем.

Алгоритм Шора

Теперь перейдем к краткому рассмотрению Алгоритма Шора, который способен разлагать большие числа на простые множители и производить дискретное логарифмирование, причем делать всё это за полиномиальное время, сводя обе эти задачи к поиску периода функции. Из-за этого вычислительно сложные задачи, лежащие в основе криптографической стойкости алгоритмов создания цифровой подписи, таких как RSA, ECDSA, ECDH, DSA, оказываются решаемыми за вменяемое время с помощью квантового компьютера, обладающего достаточной мощностью. Наличие такого квантового компьютера позволит злоумышленнику создавать ложные транзакции, тем самым получая доступ ко всем средствам, хранящимся в блокчейне, поэтому в настоящее время именно атаки с помощью алгоритма Шора считаются наиболее опасными для безопасного функционирования блокчейна.

Постквантовый блокчейн

Требования, предъявляемые к постквантовому блокчейну

Прежде чем перейти к обзору различных подходов к созданию цифровой подписи, устойчивой к квантовым атакам, рассмотрим, какие требования предъявляются к постквантовому блокчейну в целом, чтобы в дальнейшем иметь представление, какие методы могут быть использованы, а какие — нет. С одной стороны, кажется, что можно лишь увеличивать размеры ключей и хэша, чтобы отсрочить момент когда квантовые компьютеры смогут окончательно взломать блокчейн, однако такой подход имеет ряд недостатков. Во-первых, это будет требовать от устройств большого количества памяти и вычислительных ресурсов, что неприемлемо в случаях, когда с блокчейном необходимо взаимодействовать устройствам Интернета вещей, поскольку зачастую они не обладают большой памятью и мощностью, а наоборот, должны работать несколько лет от одной батарейки. Во-вторых, увеличение размера хэшей и подписей влечет за собой увеличение размера блокчейна, который необходимо хранить всем пользователям, что может занимать довольно много памяти. Такая проблема уже сейчас возникла в Bitcoin’е, размер блокчейна которого увеличился на целых 60Гб за один год и на момент написания статьи составил 310Гб, причем его рост лишь продолжает увеличиваться и, можно предположить, примерно к 2030 году он превысит 1Тб. Конечно, существует вариант использовать так называемые “легкие” кошельки, позволяющие не хранить весь блокчейн, но это уменьшает надежность системы. Таким образом, основные требования к постквантовому блокчейну касаются размеров подписей, ключей и хэшей: они не должны быть слишком большими. Кроме того, постквантовый блокчейн должен иметь достаточно большую скорость исполнения операций, чтобы обеспечивать стабильное функционирование системы с огромным количеством транзакций в секунду.

Постквантовые алгоритмы цифровой подписи

В настоящее время ведутся активные работы по разработке алгоритмов шифрования, в том числе и алгоритмов создания цифровой подписи, которые будут устойчивы к атакам с помощью квантового компьютера. Интерес исследователей подогревается тем, что в 2016 году NIST (англ.: Национальный институт стандартов и технологий) запустил конкурс таких алгоритмов, результаты которого будут объявлены к 2022 году. Приведем далее наиболее известные из предложенных алгоритмов, устойчивых к квантовым атакам.

Начнем рассмотрение с механизмов цифровой подписи на основе кода (англ.: code based), примером которой является система McEliece, предложенная примерно в то же время, что и повсеместно используемый алгоритм RSA, однако не получившая тогда широкого распространения. В настоящее время данная система, а также ряд её улучшений, таких как система Niederreiter’а, обретают всё большую популярность, поскольку они являются устойчивыми к атакам с помощью алгоритма Шора. В их основе лежит задача декодирования линейных кодов, что является NP-полной задачей, при этом пока что нерешаемой на квантовом компьютере. Несмотря на то, что подписи, сгенерированные по данным методам, обладают относительно маленьким размером и могут быть проверены достаточно быстро, они требуют хранения огромных матриц, которые выступают в роли ключей, что в свою очередь также увеличивает время генерации подписи, затрудняя её использование в блокчейне. В связи с этим исследуются различные методы сжатия матриц или использования других кодов, например, LDPC кодов (англ.: Low Density Parity Check), особенностью которых является малая плотность проверочной матрицы.

Другим механизмом создания цифровой подписи является так называемый механизм на основе решеток (англ.: lattice based), который был отдельно выделен в недавнем отчете NIST как наиболее перспективный. Так называемую решетку можно представить себе как набор точек в n-мерном пространстве с периодической структурой. В данном случае математической задачей, на которой основана криптографическая стойкость, является, например, задача нахождения в этой решетке кратчайшего вектора (Shortest Vector Problem) или же схожая с ней задача нахождения ближайшего вектора (Closest Vector Problem), причём обе эти задачи обладают огромной вычислительной сложностью. Однако недостатком таких систем является тот факт, что необходимо хранить ключи большого размера, что приводит к значительным накладным расходам шифротекста и делает практически невозможным использование подобных систем в блокчейне. Существуют, однако, системы на основе решеток, основанные на задаче краткого целочисленного решения (англ.: Short Integer Solution), благодаря чему удается уменьшить размер ключа, позволяя тем самым использовать такие системы в блокчейне.

Последним механизмом создания цифровой подписи, рассматриваемым в данной статье, является механизм на основе хэша (англ.: hash based), безопасность которого основывается не на сложности некоей математической задачи, а на лежащей в его основе криптографической хэш-функции. Подобный подход был предложен ещё в 70-х годах прошлого века как альтернатива алгоритмам RSA и DSA, однако он не пользовался большим интересом, поскольку накладывает ограничение на количество повторных использований подписей. Однако сейчас этот подход обретает всё большую популярность, поскольку он является устойчивым к квантовым атакам. Недостатком же такого подхода является тот факт, что генерация ключа занимает достаточно длительное время, что делает его неприменимым для использования в блокчейне.

Заключение

В рамках данной статьи были рассмотрены атаки с помощью квантового компьютера, к которым блокчейн оказывается уязвимым. Было выяснено, что хоть алгоритм Гровера и показывает квадратичное ускорение по сравнению с классическими подходами, атака с его помощью не несет практически никакой угрозы для существующих систем на основе proof-of-work, не говоря уже о других методах генерации блоков, таких как proof-of-stack. В то же время главной угрозой, способной свести на нет безопасное функционирование не только блокчейна, но и практически всех цифровых финансовых операций, является атака с помощью алгоритма Шора, методы борьбы с которой были также освещены в данной статье. Кроме того, были рассмотрены требования, предъявляемые к квантовому блокчейну, которые определяют, какие методы борьбы с данной атакой являются приемлемыми, а какие — нет.