Zmey56 Jun 9 2021 at 16:16

Оптимизации портфеля с помощью Python и PyPortfolioOpt

6 min

22K

Портфельная теория Марковица

Портфельная теория Марковица(далее ПТМ) (Modern portfolio theory) — разработанная Гарри Марковицем методика формирования инвестиционного портфеля, направленная на оптимальный выбор активов, исходя из требуемого соотношения доходность/риск. Сформулированные им в 1950-х годах идеи составляют основу современной портфельной теории.

Основные положения портфельной теории были сформулированы Гарри Марковицем при подготовке им докторской диссертации в 1950—1951 годах.

Рождением же портфельной теории Марковица считается опубликованная в «Финансовом журнале» в 1952 году статья «Выбор портфеля». В ней он впервые предложил математическую модель формирования оптимального портфеля и привёл методы построения портфелей при определённых условиях. Основная заслуга Марковица состояла в предложении вероятностной формализации понятий «доходность» и «риск», что позволило перевести задачу выбора оптимального портфеля на формальный математический язык. Надо отметить, что в годы создания теории Марковиц работал в RAND Corp., вместе с одним из основателей линейной и нелинейной оптимизации — Джорджем Данцигом и сам участвовал в решении указанных задач. Поэтому собственная теория, после необходимой формализации, хорошо ложилась в указанное русло.

Марковиц постоянно занимается усовершенствованием своей теории и в 1959 году выпускает первую посвящённую ей монографию «Выбор портфеля: эффективная диверсификация инвестиций».

Основа модели

1. Ожидаемая доходность портфеля(Portfolio Expected Return)

Ожидаемая доходность портфеля будет зависеть от ожидаемой доходности каждого из активов, входящих в него. Такой подход позволяет снизить риск за счет диверсификации и одновременно максимизировать доход инвестора, поскольку убытки по одним инвестициям будут компенсированы доходом по другим.

Ожидаемая доходность портфеля представляет собой суммарную ожидаемую доходность входящих в него ценных бумаг, взвешенную с учетом их доли в портфеле.

$E(R_{p}) = \sum_{i=1}^nw_{i}E(R_{i})$

2.Дисперсия портфеля (Portfolio Variance)

Дисперсия портфеля — это процесс, который определяет степень риска или волатильности, связанной с инвестиционным портфелем. Основная формула для расчета этой дисперсии фокусируется на взаимосвязи между так называемой дисперсией доходности и ковариацией, связанной с каждой из ценных бумаг, найденных в портфеле, а также с процентом или частью портфеля, который представляет каждая ценная бумага.

$\sigma_{p}^{2} = \sum_{i}^{}\omega_{i}^{2}\sigma_{i}^{2}+\sum_{i}^{}\sum_{j\neq i}^{}\omega_{i}^{}\omega_{j}^{}\sigma_{i}^{}\sigma_{j}^{}\rho_{ij}$

3.Коэффициент Шарпа (Sharpe Ratio)

$\frac{R_{p} - R_{f}}{\sigma_{p}}$

4. Эффективная граница (The Efficient Frontier)

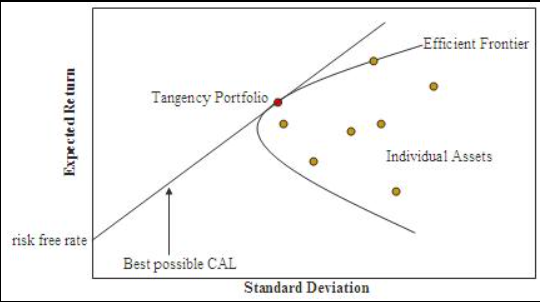
Определение и рисунок из Википедии:

Граница эффективности (англ. Efficient frontier) в портфельной теории Марковица — инвестиционный портфель, оптимизированный в отношении риска и доходности. Формально границей эффективности является набор портфелей, удовлетворяющих такому условию, что не существует другого портфеля с более высокой ожидаемой доходностью, но с таким же стандартным отклонением доходности. Понятие границы эффективности было впервые сформулировано Гарри Марковицем в 1952 году в модели Марковица.

Портфель может быть охарактеризован как «эффективный», если он имеет максимально возможный ожидаемый уровень доходности для своего уровня риска (который представлен стандартным отклонением доходности портфеля). Так, на график соотношения риска и доходности может быть нанесена любая возможная комбинация рискованных активов, и совокупность всех таких возможных портфелей определяет регион в этом пространстве. При отсутствии в портфеле безрискового актива граница эффективности определяется верхней (восходящей) частью гиперболы, ограничивающей область допустимых решений для всех соотношений активов в портфеле.

В случае же, если в портфель может быть включён безрисковый актив, граница эффективности вырождается в отрезок прямой линии, исходящий от значения доходности безрискового актива на оси ординат (ожидаемая доходность портфеля) и проходящий по касательной к границе области допустимых решений. Все портфели на отрезке между собственно безрисковым активом и точкой касания состоят из комбинации безрискового актива и рисковых активов, в то время как все портфели на линии выше и справа от точки касания образуются короткой позицией в безрисковом активе и инвестированием в рисковые активы.

Оптимизация портфеля на Python

Импорт необходимых библиотек

Как обычно в начале импортируем все необходимые библиотеки для дальнейшей работы:

import matplotlib.pyplot as plt
import numpy as np
import pandas as pd
import pandas_datareader as web
from matplotlib.ticker import FuncFormatter

Непосредственно для анализа и оптимизации портфеля существует библиотека PyPortfolioOpt. Так как она не входит в стандартный набор, то ее необходимо установить.

!pip install PyPortfolioOpt

Импортируем функции для дальнейшей работы:

from pypfopt.efficient_frontier import EfficientFrontier 
from pypfopt import risk_models 
from pypfopt import expected_returns
from pypfopt.cla import CLA
import pypfopt.plotting as pplt
from matplotlib.ticker import FuncFormatter

Получение данных по акциям из интернета

Сначала установим опять пакет, который не входит в стандартный набор. Он позволяет получить данные по акциям с сайта yahoo.

Тикеры, которые будут использоваться для анализа — одна из компаний входящих в лидеры в своем секторе.

!pip install yfinance --upgrade --no-cache-dir

import yfinance as yf
tickers = ['LKOH.ME','GMKN.ME', 'DSKY.ME', 'NKNC.ME', 'MTSS.ME', 'IRAO.ME', 'SBER.ME', 'AFLT.ME']
df_stocks= yf.download(tickers, start='2018-01-01', end='2020-12-31')['Adj Close']

df_stocks.head()

Дальше необходимо проверить есть ли среди полученных значений NaN. В случае их наличия они будут мешать дальнейшему исследованию. Для того, чтобы это решить, необходимо рассмотреть или иную акцию, или заменить их для примера средней ценой между днем до и после значения NaN.

nullin_df = pd.DataFrame(df_stocks,columns=tickers)
print(nullin_df.isnull().sum())

Расчеты

Перейдем к расчетам по оптимизации портфеля и начнем с определения ожидаемой доходности и дисперсии портфеля. Далее сохраним значения весов портфеля с максимальным коэффициентом Шарпа и минимальной дисперсией.

#Годовая доходность
mu = expected_returns.mean_historical_return(df_stocks) 
#Дисперсия портфеля
Sigma = risk_models.sample_cov(df_stocks)
#Максимальный коэффициент Шарпа
ef = EfficientFrontier(mu, Sigma, weight_bounds=(0,1)) #weight bounds in negative allows shorting of stocks
sharpe_pfolio=ef.max_sharpe() #May use add objective to ensure minimum zero weighting to individual stocks
sharpe_pwt=ef.clean_weights()
print(sharpe_pwt)

OrderedDict([('AFLT.ME', 0.0), ('DSKY.ME', 0.22606), ('GMKN.ME', 0.48796), ('IRAO.ME', 0.0), ('LKOH.ME', 0.0), ('MTSS.ME', 0.02953), ('NKNC.ME', 0.25645), ('SBER.ME', 0.0)])

Необходимо обратить внимание, что если изменить weight_bounds=(0,1) на weight_bounds=(-1,1), то в портфеле будут учитываться и короткие позиции по акциям.

Дальше посмотрим общие характеристики по портфелю.

ef.portfolio_performance(verbose=True)

Expected annual return: 37.1%
Annual volatility: 20.7%
Sharpe Ratio: 1.70
(0.37123023494063007, 0.20717177784552962, 1.695357536597058)

Теперь посмотрим портфель, который показывает минимальную волатильность:

ef1 = EfficientFrontier(mu, Sigma, weight_bounds=(0,1)) 
minvol=ef1.min_volatility()
minvol_pwt=ef1.clean_weights()
print(minvol_pwt)

OrderedDict([('AFLT.ME', 0.02876), ('DSKY.ME', 0.24503), ('GMKN.ME', 0.10403), ('IRAO.ME', 0.0938), ('LKOH.ME', 0.01168), ('MTSS.ME', 0.41967), ('NKNC.ME', 0.09704), ('SBER.ME', 0.0)])

ef1.portfolio_performance(verbose=True, risk_free_rate = 0.27)

Expected annual return: 24.0%
Annual volatility: 16.9%
Sharpe Ratio: -0.18(0.239915644698749, 0.16885732511472468, -0.17816434839774456)

Построение графика эффективных границ

Заключительным шагом является построение эффективной границы для визуального представления и расчет распределения активов.

Анализ произведем для суммы в 100 000 рублей.

cl_obj = CLA(mu, Sigma)
ax = pplt.plot_efficient_frontier(cl_obj, showfig = False)
ax.xaxis.set_major_formatter(FuncFormatter(lambda x, _: '{:.0%}'.format(x)))
ax.yaxis.set_major_formatter(FuncFormatter(lambda y, _: '{:.0%}'.format(y)))

Первым этапом посчитаем портфель с минимальной волатильностью:

latest_prices = get_latest_prices(df_stocks)
allocation_minv, rem_minv = DiscreteAllocation(minvol_pwt, latest_prices, total_portfolio_value=100000).lp_portfolio() 
print(allocation_minv)
print("Осталось денежных средств после построения портфеля с минимальной волатильностью - {:.2f} рублей".format(rem_minv))
print()

{'AFLT.ME': 41, 'DSKY.ME': 181, 'IRAO.ME': 1765, 'LKOH.ME': 1, 'MTSS.ME': 127, 'NKNC.ME': 107}
Осталось денежных средств после построения портфеля с минимальной волатильностью - 6152.03 рублей

Вторым шагом портфель с максимальным коэффициентом Шарпа:

latest_prices1 = get_latest_prices(df_stocks)
allocation_shp, rem_shp = DiscreteAllocation(sharpe_pwt, latest_prices1, total_portfolio_value=100000).lp_portfolio() 
print(allocation_shp)
print("Осталось денежных средств после построения портфеля с максимальным коэффициентом Шарпа {:.2f} рублей".format(rem_shp))

{'DSKY.ME': 167, 'GMKN.ME': 2, 'MTSS.ME': 9, 'NKNC.ME': 283} 
Осталось денежных средств после построения портфеля с максимальным коэффициентом Шарпа 1319.05 рублей

В результате нам предлагается купить для оптимального портфеля 167 акций Детского мира, 2 акции Норильского никеля, 9 акций МТС и 283 акцию Нижнекамскнефтехим. В результате у нас еще останется 1319 рублей.

Еще раз напоминаю, что все вышеприведённое не является инвестиционной рекомендацией, а только поводом к размышлению.

Tags:

Hubs: