Comments 14
Отличная статья, люблю фракталы =)
Предлагаю еще реализовать возможность сочетания различных правил фракталов между собой. Это может дать возможность породить "хаос" с использованием фракталов, которые по отдельности достаточно регулярны и отличимые от хаоса.
Я в основном экспериментировал с последовательностями и получал такие результаты.



В рамках нынешней конструкции можно ещё придумать следующее расширение: разрешить задавать различные наборы правил в зависимости от номера итерации (например, смотреть на остаток при делении на заданное число k). Это, конечно, всего лишь синтаксический сахар (т.к. полностью изоморфно увеличению количества цветов в k раз), но если аккуратно сделать (со вкладками/слайдерами или чем-то таким), то редактировать, возможно, будет удобнее. Надо подумать.
Кроме того, последнее время есть острое желание сделать бесконечное масштабирование. Кажется, что идеальной тут будет классическая схема картографических сервисов: поддержать возможность «наезжать»/«отъезжать» по колесу прокрутки, а также «таскать»
Присылайте свои фракталы в комментарии!
Пользуюсь приглашением и присылаю свой фрактал. Правда, он создан не в упомянутом «Генераторе фракталов», а в моей собственном приложении для анализа динамических систем. Тем не менее структура, которая повторяет сама себя, в нём при увеличении видна явно. Размер GIF-файла около 1.5 Мб, поэтому помещаю его под спойлер

Поиграв с генератором получилось вот так:
И вот так:
Мой результат:
Если вам интересны фракталы, то должен понравиться и этот ролик: youtu.be/Xv_JJ2ZuDJM?t=2562 (открывается с 42:42 не только ради читателей Дугласа Адамса, но и потому что именно здесь показаны правила 'Rule 110' и пример их применения).
Мне нравятся рассуждения про симметрию с точки зрения эволюции. Более симметричные объекты часто получают преимущество по критерию выживания. Вот здесь можно посмотреть ролик, как эволюционирует машинка www.youtube.com/watch?v=FKbarpAlBkw, также есть более известный пример симулятора автогонок.
Поиграться с симулятором фракталов оказалось очень занятным занятием)) Получилось успокоиться, когда получились рыбки в аквариуме, вдруг кому-то тоже понравится прилагаю. Спасибо за интересные рассуждения и приобщение общественности к мистике фракталов!
Спасибо за статью ! Удивительные аналогии и красота изложения ! Браво !
Я только не понял, за одно, получается, если принять, что люди развиваются по какому то универсальному фракталу и теоретически, зная место и время рождения ( как индивидуальный коэфициент) + формулу фрактала развития < body> каждая клетка 1x1 заменяется на блок из 3x3 клеток по девяти элементарным правилам </body> то через некоторое кол-во итераций можно будет посмотреть на красоту, представляя что это и есть свой неповторимый непонятно чего фрактал ? Интересно, а сколько итераций в 9 месяцах развития ребенка ? В одном годе? Есть ли связка со временем ? И вообще, можно ли расчитать персональный фрактал ( соединить с движением планет, например) И как его теоретически можно трактовать на уровне физических процессов в теле? Очень много вопросов , извините, если сбивчиво спросил.
Я бы не надеялся, что по такой простой модели можно что-то предсказывать про развитие ребёнка или как-то применять знание о количестве итераций за 9 месяцев беременности. В то же время, возможно, стоит прочитать статью Течение беременности у человека. В ней сказано, в частности, что «Спустя двое суток после оплодотворения эмбрион состоит из 4 клеток, спустя 3 суток — из 8 клеток, спустя 4 суток — из 10-20 клеток, спустя 5 суток — из нескольких десятков клеток. Процесс деления яйцеклетки называют «дроблением», потому что размер эмбриона не увеличивается, а каждая дочерняя клетка уменьшается в размере». Опираясь на это, теоретически можно как-то спекулировать на тему количества итераций на разных этапах.
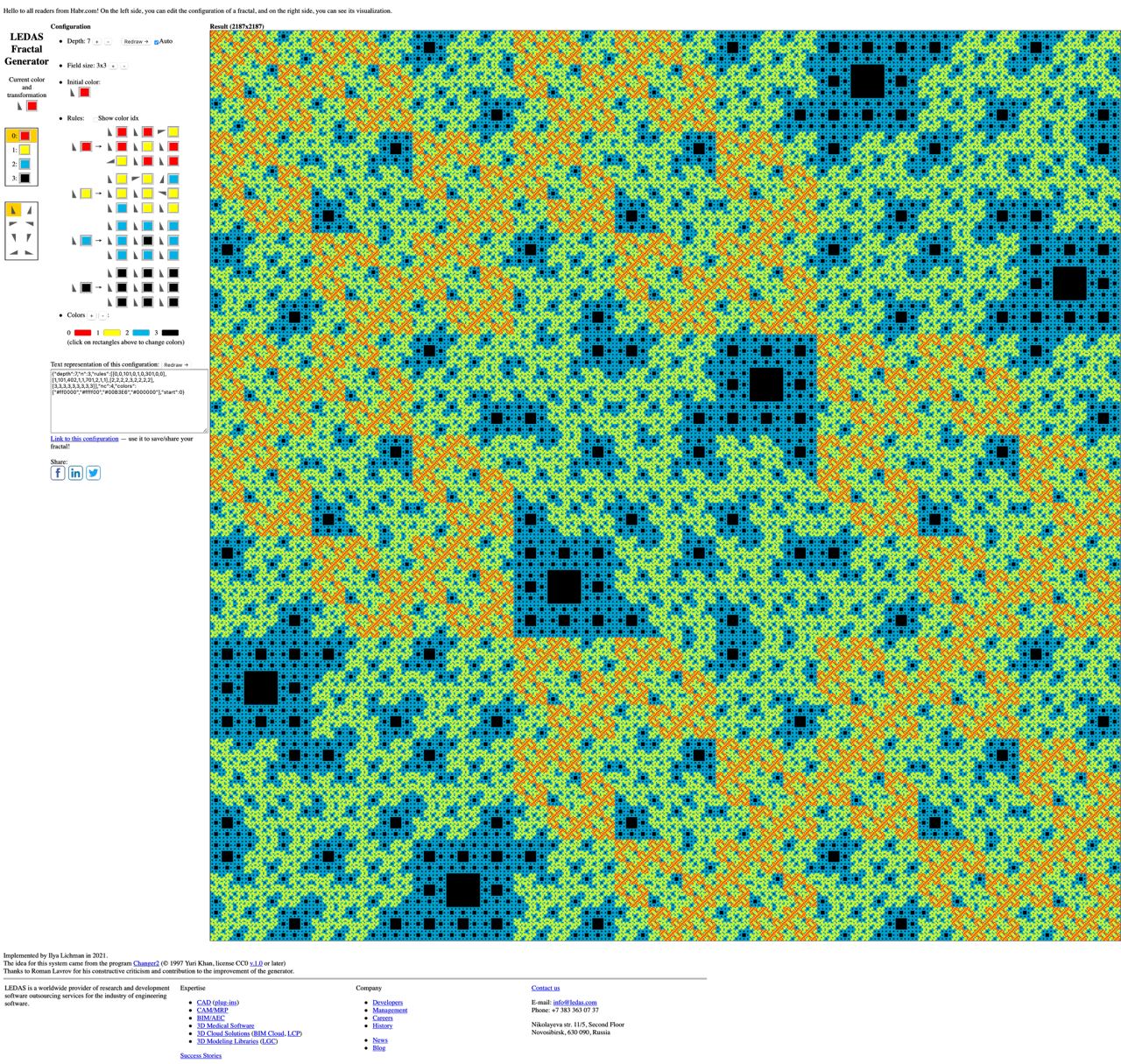



Генератор фракталов и математика внутри нас