Всем привет!
Недавно я участвовал в олимпиаде по искусственному интеллекту на Python и там было много интересных задач, но самая интересная это про звезды на небе: "Дано фото звездного неба с земли. Задача: определить количество звёзд на небе"
Вроде бы не сложно, если фотка только со звездами, например:

Ладно, тут все легко! Это можно решить так:
Импортируем библиотеки
from scipy.spatial import distance from skimage import io from skimage.feature import blob_dog, blob_log, blob_doh from skimage.color import rgb2gray import matplotlib.pyplot as plt
Я буду использовать библиотеку skimage для работы с изображением, scipy - для сложных математических вычислений и matplotlib.pyplot для отладочного вывода.
image = io.imread(input("Путь до изображения: ")) image_gray = rgb2gray(image)
Откроем изображение и преобразуем его в черно белое для его простоты его будущей обработки.
Чтобы разобраться как мы упростили представление изображения, возьмем первый пиксель в RGB и GrayScale:
print(image[0, 0]) print(image_gray[0, 0])
И получим:
[24 16 14] #RGB 0.06884627450980392 #GrayScale
работать с float проще чем с кортежем
Далее нам нужно определиться, как искать звезды. К счастью, в модуле skimage есть функция определения капель(blobs). Их три вида:
Laplacian of Gaussian (LoG)
Difference of Gaussian (DoG)
Determinant of Hessian (DoH)
Подробнее о их различиях можно прочитать тут.
На личном опыте и сравнивая результаты я пришел к выводу, что для данной задачи я буду использовать с такими параметрами.
blobs_log = blob_log(image_gray, max_sigma=20, num_sigma=10, threshold=.05)
Далее я отмечаю точки на картинке и считаю их количество
fig = plt.figure() ax = fig.add_subplot(1, 1, 1) ax.set_title('Laplacian of Gaussian') ax.imshow(image) c_stars = 0 for blob in blobs_log: y, x, r = blob if r > 2: continue ax.add_patch(plt.Circle((x, y), r, color='purple', linewidth=2, fill=False)) c_stars += 1 print("Количество звёзд: " + str(c_stars)) ax.set_axis_off() plt.tight_layout() plt.show()
Запуская, я получаю такой результат:
Количество звёзд: 353

Но верно ли отработает программа, если ввести ей картинку, которая соответствует условию задачи.

И мы получим много ложных точек.

Улучшение алгоритма
Поэтому нужно улучшить алгоритм поиска точек. Для этого воспользуемся еще одной фишкой библиотеки skimage это сегментация изображения.
Вот ссылка на источник, где описывается основы сегментации изображения.
Взяв от туда нужный кусок кода, мы улучшаем нынешний алгоритм.
Импортируем новые модули:
from skimage.segmentation import slic, mark_boundaries import numpy as np from sklearn.cluster import KMeans
Сегментируем изображение с помощью функции slic
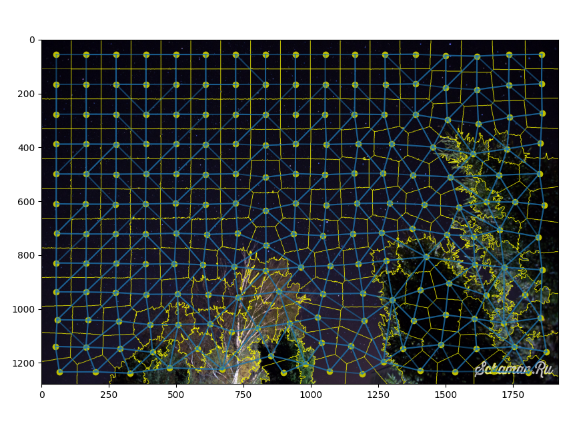
segments = slic(img, start_label=0, n_segments=200, compactness=20) segments_ids = np.unique(segments) print(segments_ids) # centers centers = np.array([np.mean(np.nonzero(segments == i), axis=1) for i in segments_ids]) print(centers) vs_right = np.vstack([segments[:, :-1].ravel(), segments[:, 1:].ravel()]) vs_below = np.vstack([segments[:-1, :].ravel(), segments[1:, :].ravel()]) bneighbors = np.unique(np.hstack([vs_right, vs_below]), axis=1) fig = plt.figure(figsize=(10, 10)) ax = fig.add_subplot(111) plt.imshow(mark_boundaries(img, segments)) plt.scatter(centers[:, 1], centers[:, 0], c='y') for i in range(bneighbors.shape[1]): y0, x0 = centers[bneighbors[0, i]] y1, x1 = centers[bneighbors[1, i]] l = Line2D([x0, x1], [y0, y1], alpha=0.5) ax.add_line(l)

Создаём словарь, для определения к какому сегменту относится каждый пиксель.
dict_seg = {} for i in range(img.shape[0]): for j in range(img.shape[1]): seg = segments[i, j] if seg not in dict_seg.keys(): dict_seg[seg] = [img[i, j]] continue dict_seg[seg].append(img[i, j])
Высчитываем средний цвет у каждого сегмента
def middle(a, b): color = [] for i, j in zip(a, b): color.append((i + j) // 2) return color for k, v in dict_seg.items(): # вычисляем перцентиль для выброса пересвеченных пикселей в сегменте p = int(0.9 * len(v)) v = sorted(list(v), key=lambda x: my_distance(x, white)) s = [0, 0, 0] for c in v: s[0] += c[0] s[1] += c[1] s[2] += c[2] s[0] //= len(v[:p]) s[1] //= len(v[:p]) s[2] //= len(v[:p]) dict_seg[k] = s
На выходе получаем словарь со средними цветами в каждо�� сегменте
>>> {0: [5, 3, 14], 1: [5, 3, 16], 2: [7, 4, 17] ... 190: [23, 19, 37]}
Далее кластеризуем словарь dict_segс помощью KMeans из библиотеки sklearn
kmeans = KMeans(n_clusters=3, algorithm="elkan") kmeans.fit(list(dict_seg.values())) labels, counts = np.unique(kmeans.labels_, return_counts=True)
Создаем новый словарь вида {segment: claster_num(их всего 3)}
dic_seg_claster = {} for key, value in dict_seg.items(): dic_seg_claster[key] = kmeans.predict([value])[0] max_l = max(dic_seg_claster.values(), key=lambda x: list(dic_seg_claster.values()).count(x))
Находим максимально частый кластер на картинке
Далее идет наш предыдущий код, но с некоторыми изменениями:
blobs_log = blob_log(image_gray, max_sigma=30, num_sigma=10, threshold=.05) fig = plt.figure() ax = fig.add_subplot(1, 1, 1) ... for blob in blobs_log: y, x, r = blob # новый фрагмент if dic_seg_claster[segments[int(y), int(x)]] == max_l: c = plt.Circle((x, y), r, color='purple', linewidth=2, fill=False) count += 1 ax.add_patch(c) ...
И уже получаем результат получше.

Высчитав статистическую вероятность, пришел к выводу, что погрешности на лишних объектах компенсируют невыделенные звезды.
Этот алгоритм ещё можно долго улучшать, подстраивать количество сегментов и кластеров. Но на данный момент я приостановлюсь.
Все ваши пожелания или негодования оставляйте а комментариях, мне будет очень интересно прочитать их, для того чтобы улучшить мой алгоритм до идеального состояния)
Готовый проект можно найти в gitHub
Спасибо за внимание!