В данной статье рассматривается простой алгоритм распознавания нарисованного пользователем многоугольника. Алгоритм преобразует набор точек, предоставленный пользователем, в точки многоугольника, удаляя точки находящиеся на прямых. Так же алгоритм может на базовом уровне распознавать окружности.
Данный алгоритм не претендует на уникальность. Однако, я постарался детально расписать как и почему он работает без сложной математики, за исключением, быть может свертки.
Оглавление
Общее описание алгоритма
Алгоритм преобразует точки, предоставленные пользователем, в диаграмму удаленности точки от центра. По полученным расстояниям строится диаграмма распределение расстояния в зависимости от угла. Далее к диаграмме применяется простая свертка, позволяющая выделить углы многоугольника. Если после применения фильтра не найдено ни одного угла, то считается, что пользователь нарисовал окружность. В противном случае выполняется поиск всех углов многоугольника. Если число найденных углов больше пяти, то многоугольник считается не распознанным.
Полный код проекта доступен в этом репозитории. Проект представляет из себя GUI-приложение на Java, в котором можно нарисовать фигуру и посмотреть как она распознается. Главная задача проекта — реализовать алгоритм распознавания, поэтому местами вид кода заставляет плакать.
Весь код относящийся к алгоритму распознавания находится в файле Algorithm.java.
Преобразование точек в диаграмму
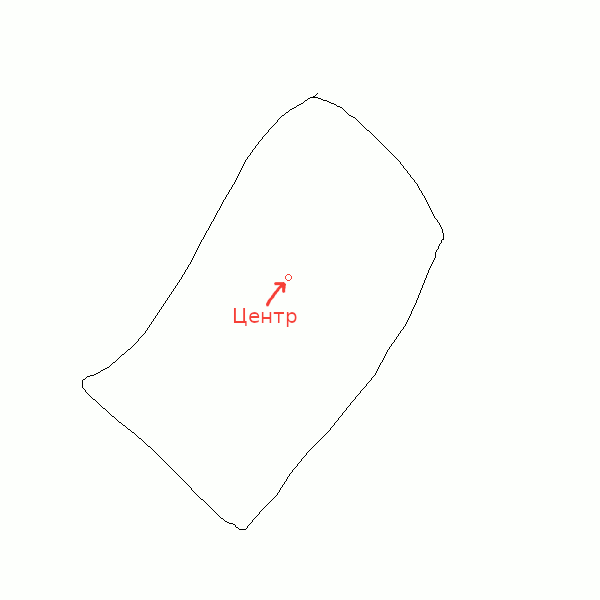
Как правило, углы многоугольника находятся дальше от его центра, чем ближайшие к ним точки. Значит построив график расстояния от каждой точки до центра многоугольника можно определить какие из точек являются его углами, а какие находятся на ребрах.
В качестве центра многоугольника можно использовать среднее арифметическое всех точек. Далее можно посчитать расстояние от центра до каждой точки.
Код преобразования точек в массив расстояний
// Расчет центра фигуры.
int centerX = 0;
int centerY = 0;
for (Point point : sourcePoints) {
centerX += point.x;
centerY += point.y;
}
centerX /= sourcePoints.size();
centerY /= sourcePoints.size();
// Расчет расстояний от точек до центра.
distancies.clear();
for (int index = 0; index < sourcePoints.size(); index += 1) {
Point point = sourcePoints.get(index);
Distance distance = new Distance();
int deltaX = point.x - centerX;
int deltaY = point.y - centerY;
distance.distance = Math.pow(deltaX, 2) + Math.pow(deltaY, 2);
distance.angle = Math.atan2(deltaX, deltaY);
distance.index = index;
distancies.add(distance);
}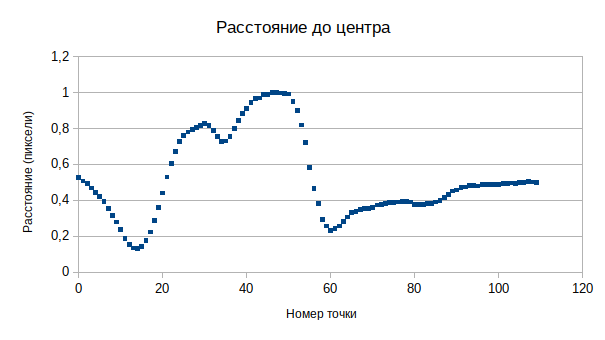
На данном графике можно выделить четыре точки, предположительно соответствующие углам многоугольника. Однако, выбрать будущий угол многоугольника достаточно сложно даже человеку. Чтобы упростить распознавание преобразуем график, следующим образом: вместо индекса точки будем использовать угол, на котором расположена точка, относительно центра фигуры.
Код преобразования массива расстояний в массив углов
Collections.sort(distancies, Comparator.comparingDouble((Distance d) -> d.angle));
// Нормализуем расстояния, чтобы дальнейшие расчеты не зависили от размера фигуры.
double minimalAngle = 0.0;
double maximalAngle = 0.0;
double maximalDistance = 0.0;
for (Distance distance : distancies) {
minimalAngle = Math.min(distance.angle, minimalAngle);
maximalAngle = Math.max(distance.angle, maximalAngle);
maximalDistance = Math.max(distance.distance, maximalDistance);
}
for (Distance distance : distancies) {
distance.distance = distance.distance / maximalDistance;
distance.position = data.length * (distance.angle - minimalAngle) / (maximalAngle - minimalAngle);
}
// Вычислим массив расстояний, в котором угол будет изменяться линейно относительно индекса в массиве.
for (int index = 0; index < data.length; index += 1) {
Distance dd = new Distance();
dd.position = index;
int found = Collections
.binarySearch(distancies, dd, Comparator.comparingDouble((Distance d) -> d.position));
if (found >= 0) {
data[index] = distancies.get(found).distance;
} else {
int point = -found - 1;
Distance left = distancies.get(point - 1);
Distance right = distancies.get(point);
double factor = (index - left.position) / (left.position - right.position);
data[index] = left.distance + factor * (left.distance - right.distance);
if (factor < 0.5) {
indexes[index] = point - 1;
} else {
indexes[index] = point;
}
}
}
На данном графике уже можно определить точки, соответствующие углам многоугольника. Каждая такая точка имеет характерный пик, по которому можно определить угол и саму точку. Для упрощения распознавания пиков, соответствующих точкам, выполним преобразование данного графика при помощи свертки.
Поиск углов многоугольника
Для того, чтобы алгоритм мог выделить пики, соответствующие углам воспользуемся ядром свертки, построенным на основании расстояния до точек, принадлежащих углу четырехугольника, по следующей формуле:
Код расчета ядра свертки
// dataSize - размер массива с расстояниями до центра
public static Kernel peakDetect(int dataSize) {
// data length / (2 * max corners + 1)
int size = dataSize / (2 * 5 + 1);
// Middle element of array
int center = (size / 2) | 1;
double values[] = new double[size];
double kernelSum = 0.0;
for (int index = 0; index < size; index += 1) {
double factor = Math.abs(index - center) / (center + 1.0);
values[index] = Math.sqrt(Math.pow(1 - factor, 2.0) + 1) - 1;
kernelSum += values[index];
}
for (int index = 0; index < size; index += 1) {
values[index] += -kernelSum / size;
}
return new Kernel(values, center);
}Данная формула рассчитывает расстояние до точек квадрата о 0 до 45 градусов.
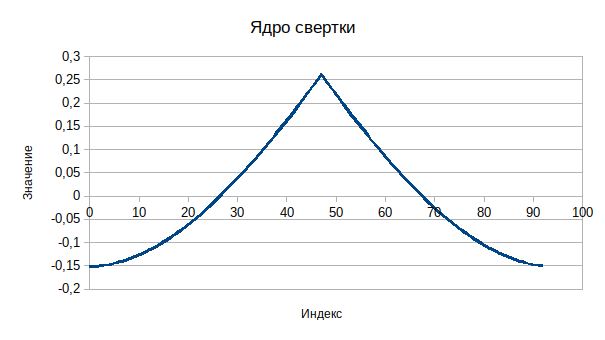
Данное ядро было выбрано по двум причинам — оно достаточно простое для понимания и оно дает достаточно хорошее приближение к реальности. Тем не менее возможно подобрать лучший вариант.
Код свертки расстояний с истолькованием ядра
// data - исходные расстояния до центра, приведенные к диапазону 0..1
// result - результат свертки
public void apply(double[] data, double[] result) {
for (int dataIndex = 0; dataIndex < data.length; dataIndex += 1) {
double sum = 0.0;
for (int kernelIndex = 0; kernelIndex < values.length; kernelIndex += 1) {
int offset = dataIndex + kernelIndex - center;
if (offset < 0) {
offset += data.length;
}
if (offset >= data.length) {
offset -= data.length;
}
sum += values[kernelIndex] * data[offset];
}
result[dataIndex] = sum;
}
}Применив свертку к графику, представленному на рисунке 3, получим график, на котором значения, соответствующие пикам, достаточно хорошо выделены.

На данном графике можно выделить четыре пика, соответствующие точкам многоугольника. Для выделения точек используем следующий алгоритм:
Выделим все области, где значение больше нуля, каждая область будет соответствовать одной точке;
Для каждой области найдем максимальное значение на графике. Будем считать, что данное значение соответствую искомому углу многоугольника;
Найден точку, соответствующую найденному значению в исходных данных и добавим ее в список углов многоугольника;
Если найдено слишком много углов, то будем считать фигуру окружностью.
Код нахождения углов многоугольника
// Выбирает начальную позицию так, чтобы она находилась на границе.
int startIndex = 0;
while (startIndex < filtered.length && filtered[startIndex] >= 0.0) {
startIndex += 1;
}
while (startIndex < filtered.length && filtered[startIndex] < 0.0) {
startIndex += 1;
}
// Для каждого пика выбираем точку с максимальным значением.
List<Distance> found = new ArrayList<>();
boolean inPoint = true;
double maxValue = filtered[startIndex];
int maxIndex = indexes[startIndex];
for (int index = 0; index < filtered.length; index += 1) {
int offset = index + startIndex;
if (offset >= filtered.length) {
offset -= filtered.length;
}
double value = filtered[offset];
if (value >= 0.0 && inPoint) {
if (maxValue < value) {
maxValue = value;
maxIndex = offset;
}
} else if (value >= 0.0 && !inPoint) {
maxValue = value;
maxIndex = offset;
inPoint = true;
} else if (value < 0.0 && inPoint) {
Distance distance = distancies.get(indexes[maxIndex]);
found.add(distance);
inPoint = false;
} else if (value < 0.0 && !inPoint) {
}
}
Распознавание окружностей
Данный алгоритм в любой окружности способен найти многоугольник. Для того, чтобы отсеять подобные многоугольники необходимо добавить дополнительную фильтрацию окружностей. Будет считать фигуру окружностью в том случае, если после свертки нет ни одного значения больше 1. Это будет означать, что фигура не имеет ни одного ярко выраженного угла, а значит ее можно считать окружностью.
Код распознавания окружности
boolean isCircle = true;
for (double value : filtered) {
if (value > 1.0) {
isCircle = false;
break;
}
}

Данный критерий не подходит для распознавания эллипсов, сильно вытянутых в одном направлении. Это связано с тем, что такие эллипсы имеют пики, подобные углам многоугольника.

Отличить эллипс возможно по числу найденных углов. Если алгоритмом было найдено два угла, то, вероятно, фигура является эллипсом. Однако, такая проверка не была реализована в рамках данного проекта.
Что можно улучшить
Использовать центр масс вместо простого среднего значения. Это должно лучше выделять пики, соответствующие углам;
Улучшить распознавание окружностей. Сейчас они просто вписываются в прямоугольник, содержащий все точки;
Реализовать распознавание не только центра эллипса, но и его поворота;
Использовать промежуточные точки, чтобы точнее построить ребро многоулгольника;
Выбрать хорошее ядро для фильтрации расстояний.
Заключение
Предложенный алгоритм справляется со своей задачей. Он достаточно хорошо распознает простые фигуры, за исключением окружностей.

Весь код доступен в этом репозитории.