Этой небольшой заметкой я хочу начать цикл статей посвященных алгоритмам компьютерной графики. Причем, не аппаратным тонкостям реализации этой самой графики, а именно алгоритмической составляющей.
Действовать буду по следующему принципу: беру какой-либо графический эффект (из демо, программы, игры – не важно) и пытаюсь реализовать этот же эффект максимально простым и понятным способом, разъясняя что, как и почему сделано именно так.
В качестве основы для вывода графики будет использован язык Python и библиотека PyGame. Этим набором можно очень просто что-то выдать на экран, сделать анимацию и т.п. не отвлекаясь на технические детали реализации.
За базовый шаблон программы возьму вот такой код:
import pygame
SX = 800
SY = 800
pygame.init()
screen = pygame.display.set_mode((SX, SY))
running = True
while running:
for event in pygame.event.get():
if event.type == pygame.QUIT:
running = False
# Здесь будет алгоритмическая часть
pygame.display.flip()
pygame.quit()
Это маленькая заготовка, которая позволяет сформировать окно для вывода графики, а также формирует бесконечный цикл воспроизводящий кадр анимации, выдаваемый на экран - так называемый игровой цикл.
По вышеуказанному коду останавливаться не буду, думаю здесь все максимально понятно. Давайте сразу перейдем к делу.
Что для начала можно взять из графических эффектов, чтобы было и максимально просто и максимально красиво?
Давным-давно существовал такой класс программ, который назывался «хранителями экрана». Это небольшие программы, которые демонстрировали незамысловатую анимацию и запускались по таймеру, когда пользователь не нажимал никакие клавиши или не трогал мышь. Они существуют до сих пор, но сейчас несут более эстетический функционал, чем практический. В эпоху мониторов на электронно-лучевых трубках такие программы помогали предотвратить выгорание люминофора внутри кинескопа.
Если на экране монитора долго показывать статичное изображение с минимум изменений, то можно получить эффект того, что люминофор, нанесенный на внутреннюю сторону кинескопа, из-за перегрева в отдельных точках испарялся и оставались следы, которые не исчезали даже при отключении питания монитора. Т.е. изображение оставалось как бы выжженное на мониторе. Кстати, этому эффекту подвержены и ЖК мониторы и плазменные панели и др.

Чтобы такого эффекта не возникало, при длительном бездействии пользователя запускалась программа-скринсейвер, которая обновляла экран и отображала что-нибудь меняющееся, не давая шанса выгореть отдельным частям экрана.
Получается, что полезный функционал соединял в себе еще и эстетическую составляющую, поскольку всем хотелось видеть на своем мониторе что-то приятное глазу.
Одной из таких программ была демонстрация звездного неба, где просто мигали отдельные звездочки. Но еще красивее выглядел полет сквозь звезды.
Вот несколько примеров таких хранителей экрана и программных продуктов, где они были интегрированы:


Давайте за основу возьмем хранитель экрана из Windows 3.11 и попытаемся его повторить, возможно, с небольшими улучшениями.
Если взглянуть на анимацию, то мы видим какое-то количество звезд, которые движутся на нас. Звезды приближаются постепенно увеличивая свою яркость. Разлет звезд происходит равномерно относительно центра экрана.
Начнем с того, что нам нужно как-то зафиксировать общее количество звезд, которое одновременно мы будем отображать на экране.
Пусть это будет константа NumStar и для начала обрабатывать будем 100 звезд.
Звезды нужно где-то хранить, поскольку мы используем Python, пусть это будет обычный изменяемый список. Каждая звезда имеет какие-то характеристики, их и будем записывать в этот список.
Что нам нужно знать о звезде:
Её координаты в пространстве. Так как мы эмулируем звезды в трехмерном пространстве, то это будут координаты X, Y, Z.
Z будет являться глубиной экрана, чем оно больше, тем звезда дальше.
Характеристика цвета звезды, она же яркость. Чем звезда дальше, тем она будет тусклее, поэтому значение цвета будет обратно пропорционально расстоянию до звезды.
Получится примерно следующее: Звезды[ [x1, y1, z1, color1], [x2, y2, z2, color2], и т.д.]
Когда звезда летит к нам она постепенно двигается по всем трем координатам X, Y, Z, и когда-нибудь она вылетит за границы экрана. Выпасть из нашей области видимости звезда может, если она превысила координаты на плоскости нашего окна по X или Y, а также, если она слишком близко подлетела к нам и перешла в отрицательные координаты по оси Z. В этот момент нужно вместо этой звезды сделать новую звезду, чтобы не обрабатывать зря значения, которых мы никогда не увидим.
Самый для этого способ, это сбросить все свойства звезды на какие-то начальные значения.
Поскольку нам нужно, чтобы звезды летели к нам равномерно относительно центра экрана, то для себя решим, что центр нашего окна, будет являться центром системы координат, что конечно не совпадает с координатами предоставляемыми PyGame, но это легко подменяется.
Для равномерного случайного разброса координат звезд по плоскости нашего окна применим такой подход: нам известна ширина и высота окна (это SX и SY), поэтому новые координаты будем получать как:
X = random.randint(0, SX) - SX // 2
Y = random.randint(0, SY) - SY // 2
Т.е. мы получаем случайное число в диапазоне от 0 до ширины или высоты нашего окна, а затем делим его нацело на 2 и получаем случайное число в диапазоне от «–половина окна» до «+половина окна». Координаты X и Y готовы.
Координата по Z задается проще, каждая новая звезда появляется на максимальном удалении от нас. Для простоты расчетов пусть максимальная глубина экрана будет 256.
Поэтому Z = 256.
И остается цвет новой звезды, но поскольку она далеко, пусть звезда сначала будет не видна, т.е. дадим ей цвет 0.
сolor = 0
По мере приближения звезды к нам по оси Z, ее яркость будет возрастать. И увеличиваться от 0 до 255.
Приблизительная схема алгоритма получается такая:
Перед основным циклом анимации производим первоначальную инициализацию всех звезд.
Анимация будет состоять из следующих шагов:
очищаем экран;
выводим звезды;
просчитываем новые координаты;
повторяем.
Для отображение звезды уже в экранных координатах, нам нужно выполнить преобразование 3D координат в 2D, и желательно в перспективной проекции.
Давайте попробуем теоретически разобрать как это сделать.
Во первых что такое перспективная проекция - это когда для построения проекции нам нужна некая точка - центр проекции, из нее выходит луч, который пересекает объект для которого строится проекция и некую плоскость, на которой проецируется объект. Такой способ позволяет отображать объект на плоскости учитывая его перспективные искажения, т.е. дальние части будут меньше чем ближние.
На рисунке ниже я представлю мою звезду в координатах X, Y, Z. Сейчас рассматривается только две оси Y и Z, для оси X и Z все будет совершенно аналогично. Центр проекции будет располагаться в начале координат. Из центра проекции выходит виртуальный луч, который пересекает звезду и в дальнейшем пересекает плоскость моего экрана, на котором в 2D виде, будут отображаться звезда (оси Z здесь уже не будет).
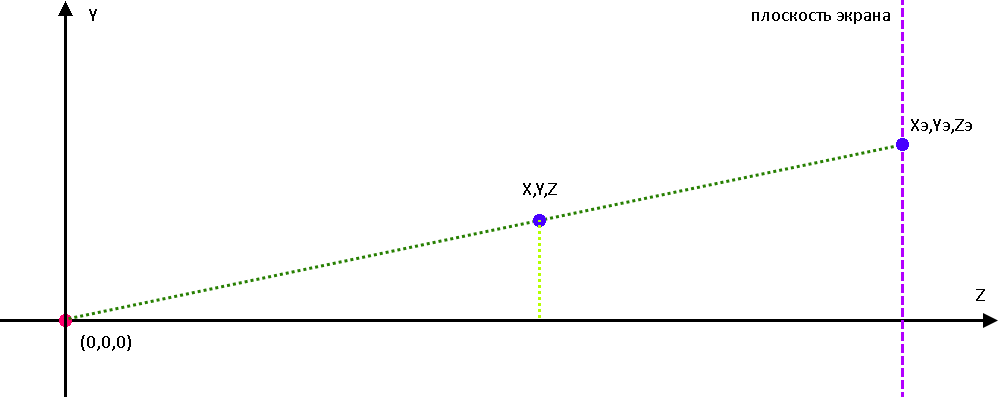
Это можно сравнить с фонариком, который светит из центральной точки и звезда отбрасывает тень, на некую стену (мой экран).
Точка на экране будет иметь координаты. Поскольку мы сейчас рассматриваем оси Y и Z, X в расчет не берем.
Мне нужно вычислить координату.
Здесь уместно вспомнить шко��ьный курс геометрии и теорему подобия треугольников, которая гласит что отношения подобных сторон у подобных треугольников равны. Соответственно будет справедливо следующее утверждение:
Исходя из этого вычислим:
Поместим плоскость для отображения в самую дальнюю точку нашего виртуального поля по оси Z, в координату 256. В итоге получим формулы для вычисления экранных координат наших звезд на плоскости в следующем виде:
Но поскольку мы немножко модицифицировали наш центр координат, по сравнению с тем, что предлагает PyGame (а он считает начало координат из верхнего левого угла окна), нам нужно привести полученные координаты к системе координат PyGame.
В итоге при движении звезды к центру координат по оси Z, она будет перемещаться по оси Y вверх, и будет происходить эффект разбегания звезд из центра экрана.
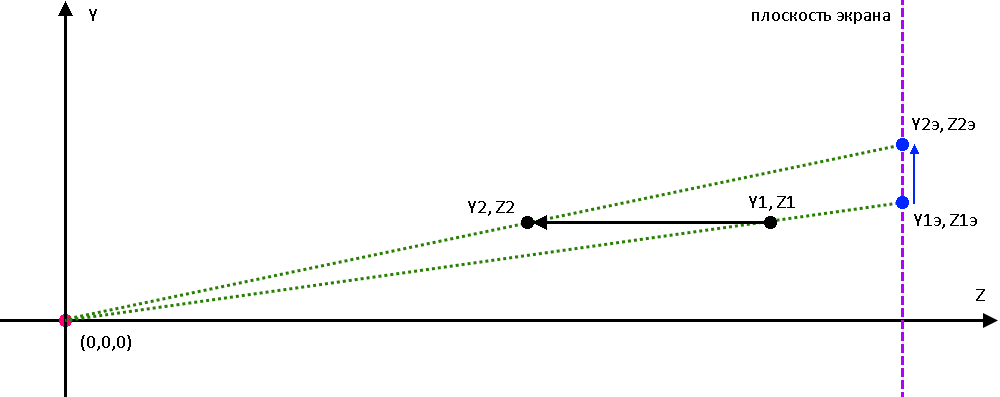
Сделаем движение всех звезд с одинаковой скоростью - speed. Скорость выберем экспериментальным путем, у меня она получилась равной 0,09, для медленного и красивого движения звезд.
В цикле, для каждой звезды уменьшаем ее Z координату и пересчитываем X и Y. Если координата по Z стала меньше или равной 0 или звезда вылетела за любую из боковых границ экрана по X или Y, то генерируем новую звезду, вместо старой.
Одновременно с уменьшением координаты по Z, увеличиваем значение цвета звезды, чтобы при ее приближении к нам, яркость возрастала. Опытным путем приращение яркости, для наиболее приятной картинки, у меня получилось с шагом в 0.15.
И итоговый код получится следующий:
import pygame
import random
SX = 800
SY = 800
pygame.init()
screen = pygame.display.set_mode((SX, SY))
running = True
NumStar = 100 # Общее количество звезд
speed = 0.09 # Скорость полета звезд
stars = [] # Список, содержащий звезды
# каждая звезда состоит из X-координаты, Y-координаты,
# расстояния по Z (дальность до звезды), цвет
# -----------------------------------------------------------------------------------
# Функция генерации новой звезды.
# -----------------------------------------------------------------------------------
def new_star():
star = [random.randint(0, SX) - SX // 2, random.randint(0, SY) - SY // 2, 256, 0]
return star
# -----------------------------------------------------------------------------------
for i in range(0, NumStar): # Заполняем список новыми сгенерированными звездами.
stars.append(new_star())
while running:
for event in pygame.event.get():
if event.type == pygame.QUIT:
running = False
screen.fill((0, 0, 0)) # Очищаем экран
x = y = 0
for i in range(0, NumStar): # Цикл по всем звездам.
s = stars[i] # Запоминаем характеристики звезды из списка
# Вычисляем текущие координаты звезды
x = s[0] * 256 / s[2]
y = s[1] * 256 / s[2]
s[2] -= speed # Изменяем ее координату по Z
# Если координаты вышли за пределы экрана - генерируем новую звезду.
if s[2] <= 0 or x <= -SX // 2 or x >= SX // 2 or y <= -SY // 2 or y >= SY // 2:
s = new_star()
if s[3] < 256: # Если цвет не достиг максимума яркости, увеличиваем цвет.
s[3] += 0.15
if s[3] >= 256: # Если вдруг цвет стал больше допустимого, то выставляем его как 255
s[3] = 255
stars[i] = s # Помещаем звезду обратно в список звезд.
# Отображаем звезду на экране.
x = round(s[0] * 256 / s[2]) + SX // 2
y = round(s[1] * 256 / s[2]) + SY // 2
pygame.draw.circle(screen, (s[3], s[3], s[3]), (x, y), 3)
pygame.display.flip()
pygame.quit()
Получаем аналог "древнего" хранителя экрана на языке Python. Данный алгоритм и графический эффект является одним из простейших, но содержит в себе немного интересной математики и геометрических преобразований.

В следующей части мы попробуем реализовать эффект плавающего туннеля из демо 1993 года "SecondReality" от группы Future Crew.
