• The method of phase-magnitude interpolation (PMI)
• Accurate measure of frequency, magnitude and phase of signal harmonics
The Fast Fourier Transform (FFT) algorithm is an important tool for analyzing and processing signals of various nature.
It allows to reconstruct magnitude and phase spectrum of a signal into the frequency domain by magnitude sample into the time domain, while the method is computationally optimized with modest memory consumption.
Although there is not losing of any information about the signal during the conversion process (calculations are reversible up to rounding), the algorithm has some peculiarities:
resolution, a kind of "discrete pixelization" like a histogram
the effect of spectral leakage, which causes the characteristic spreading of information along the histogram bars for those signal harmonics whose frequency does not fall very accurately on divisions of the discrete frequency grating
These factors hinder high-precision analysis and fine processing of results further.

The article presents an effective way to overcome such "inconvenient" features of the algorithm.
The materials are provided with illustrations, however, for a deeper dive into the topic, it is recommended to download the Solfeggio desktop application for high-precision signal processing and visualization. With its help, you can examine a signal in details and "probe" its spectrums at various scale levels: from the overall picture up to particular discrete samples.
IMPORTANT! The program and algorithmic developments are free for educational and non-commercial use, but there are a range of important restrictions on usage scopes. Please, before intercalation the presented developments in any projects, carefully read the small agreement...
In the process of creating Solfeggio the patterns had been revealed, which led to the development of phase-magnitude interpolation algorithm for fast Fourier transform (PMI for FFT). At the same time, unsolved problems were formulated.
Now let's go briefly through the main stages and provisions of the theory of signal processing:
a receiver (microphone or other sensor) picks up an analog signal and converts it into equivalent voltage oscillations of electricity
an analog-to-digital converter (ADC) with a given frequency (via regular time intervals) measures the voltage level of the input signal and forms an array (frame) of its time discrete samples quantized by the magnitude level
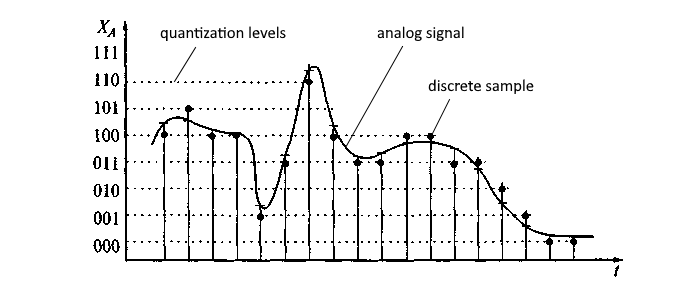
then, on the basis of the generated frame, the direct FFT is calculated, as a result of which an array of spectral data is obtained at output, it gives some representation of the harmonics of the original analog signal (magnitudes and phases of dominant frequencies), that allows to reconstruct properties of the source analog signal with a certain error (see Fig. 1)
As mentioned earlier, because the spectral representation is discrete and not analog, it has inherent resolution, a kind of histogram-like pixelization, and can also exhibit spectral leakage, which causes a characteristic spreading of information about the harmonics of the signal, the frequency of which does not fall quite accurately at divisions of a discrete frequency grating. In practice, these phenomena complicate the subsequent reconstruction and analysis of the original signals.
It is important to note that the applying of the inverse FFT to the resulting array of spectral data makes it possible to definitely restore the original discrete signal in the time domain (up to rounding), which indicates that there is not information lost from the signal during the conversion. It means that calculations are reversible.
In turn, according to the Nyquist-Shannon-Kotelnikov theorem, an analog signal can be unambiguously and without distortion restored from its discrete time samples, when the sampling frequency is at least twice the frequency of the highest frequency harmonic of the signal. This suggests that by interpolating a discrete signal in the time domain (back to analog) and increase sample rate (re-sampling), higher resolution in the phase-frequency domain can be achieved at the expense of increased computational complexity and memory consumption. This approach is possible, but not always convenient in practice.
RIDDLE №1
But since it is possible to interpolate a signal in the time domain of representation, maybe there is some kind of interpolation method in the frequency domain? Although there is no mathematical justification for this hypothesis for the moment of this article writing, experimental data indicate that a such approach exists for low-noise signals, and for many common practical situations it gives very accurate and reliable results.
RIDDLE №2
Although the accuracy of the method is high, however, some error is inherent in it. Perhaps this error can be reduced by refining the formulas. The question also remains open.
The interpolation method is intuitive and surprisingly computationally simple. It was experimentally discovered during the development of the Solfeggio tool for high-precision spectral analysis.
So, first, consider the classic Fast Fourier Transform algorithm in C#. Below there are two modifications of the "butterfly" operation (with decimation in time and in frequency), which differ in the order and structure of the cycles, but ultimately lead to the same result
private static void DecimationInFrequency(ref Complex[] sample, bool direct)
{
if (sample.Length < 2) return;
var length = sample.Length / 2; // sample.Length >> 1
var sampleA = new Complex[length];
var sampleB = new Complex[length];
var abs = (Pi.Single / length).InvertSign(direct);
var rotorBase = new Complex(Cos(abs), Sin(abs));
var rotor = Complex.One; // rotor = rotorBase.Pow(0)
for (int i = 0, j = length; i < length; i++, j++)
{
var a = sample[i];
var b = sample[j];
sampleA[i] = a + b;
sampleB[i] = (a - b) * rotor;
rotor *= rotorBase; // rotor = rotorBase.Pow(i + 1)
}
DecimationInFrequency(ref sampleA, direct);
DecimationInFrequency(ref sampleB, direct);
for (int i = 0, j = 0; i < length; i++) // j += 2
{
sample[j++] = sampleA[i];
sample[j++] = sampleB[i];
}
}
private static void DecimationInTime(ref Complex[] sample, bool direct)
{
if (sample.Length < 2) return;
var length = sample.Length / 2; // sample.Length >> 1
var sampleA = new Complex[length];
var sampleB = new Complex[length];
var abs = (Pi.Single / length).InvertSign(direct);
var rotorBase = new Complex(Cos(abs), Sin(abs));
var rotor = Complex.One; // rotor = rotorBase.Pow(0)
for (int i = 0, j = 0; i < length; i++) // j+=2
{
sampleA[i] = sample[j++];
sampleB[i] = sample[j++];
}
DecimationInTime(ref sampleA, direct);
DecimationInTime(ref sampleB, direct);
for (int i = 0, j = length; i < length; i++, j++)
{
var a = sampleA[i];
var b = sampleB[i] * rotor;
sample[i] = a + b;
sample[j] = a - b;
rotor *= rotorBase; // rotor = rotorBase.Pow(i + 1)
}
}
Normalization of values after the "butterfly" operation performs by the following way
public static partial class Butterfly
{
public static Complex[] Transform(this IEnumerable<Complex> sample, bool direct, bool inTime = false)
{
var workSample = sample.ToArray();
if (inTime) DecimationInTime(ref workSample, direct);
else DecimationInFrequency(ref workSample, direct);
double factor = direct ? workSample.Length / 2 : 2;
for (var i = 0; i < workSample.Length; i++) workSample[i] /= factor;
return workSample;
}
}
The method of phase-magnitude interpolation (PMI)
Now consider the method of phase-magnitude interpolation (PMI).
public static IEnumerable<Bin> Interpolate(this IList<Bin> spectrum, List<int> resonances = default)
{
resonances?.Clear();
var count = spectrum.Count / 2 - 4;
for (var i = 0; i < count; i++)
{
/* Frequency (F); Magnitude (M); Phase (P); */
spectrum[i + 0].Deconstruct(out var aF, out var aM, out var aP);
spectrum[i + 1].Deconstruct(out var bF, out var bM, out var bP);
spectrum[i + 2].Deconstruct(out var cF, out var cM, out var cP);
spectrum[i + 3].Deconstruct(out var dF, out var dM, out var dP);
double GetPeakProbabilityByPhase() => Math.Abs(cP - bP) / Pi.Single;
double GetPeakProbabilityByMagnitude()
{
var bcM = (bM + cM) - (aM + dM) / Pi.Half;
return
(aM < bcM && bcM > dM)
&&
(bM * 0.95 < bcM && bcM > cM * 0.95)
? 0.95
: 0.05;
}
var peakProbabilityByPhase = GetPeakProbabilityByPhase();
var peakProbabilityByMagnitude = GetPeakProbabilityByMagnitude();
var peakProbability = peakProbabilityByPhase * peakProbabilityByMagnitude;
if (peakProbabilityByMagnitude > 0.5 && peakProbabilityByPhase < 0.5)
resonances?.Add(i);
if (peakProbability > 0.5)
{
/*
var halfStepF = (cF - bF) / 2;
var bcMiddleF = (bF + cF) / 2;
var bcOffsetScale = (cM - bM) / (cM + bM);
var bcF = bcMiddleF + bcOffsetScale * halfStepF;
*/
var bcF = (bF * bM + cF * cM) / (bM + cM);
var bcM = (bM + cM) - (aM + dM) / Pi.Half;
var bcP = bP + (bcF - bF) * (cP - bP) / (cF - bF);
/* y(x) = y0 + ( x - x0) * (y1 - y0) / (x1 - x0) */
var abF = aF + (bcF - bF);
var abM = aM;
var abP = aP;
var dcF = dF + (bcF - cF);
var dcM = dM;
var dcP = dP;
yield return new(in abF, in abM, in abP);
yield return new(in bcF, in bcM, in bcP);
yield return new(in dcF, in dcM, in dcP);
i += 3;
}
else
{
yield return new(in aF, in aM, in aP);
}
}
}
Accurate measure of frequency, magnitude and phase of signal harmonics
There are three key lines
var bcF = (bF * bM + cF * cM) / (bM + cM);
var bcM = (bM + cM) - (aM + dM) / Pi.Half;
var bcP = bP + (bcF - bF) * (cP - bP) / (cF - bF);
/* y(x) = y0 + ( x - x0) * (y1 - y0) / (x1 - x0) */Exactly by these formulas the frequency, magnitude and phase of a leaked over the spectrum harmonic calculates with fairly high accuracy. The first and third formulas for frequency and phase had been derived intuitively, the second for magnitude had been chosen experimentally. At the time this article writing strictly mathematical justification for these formulas have not found.
Noteworthy that presented formulas work best for a rectangular window, that is, they do not require additional preprocessing of a discrete frame. Using any other window functions only reduces their accuracy.
The presence of several nearby harmonics in the spectrum can introduce additional distortions into the interpolation accuracy, but for remote from each other harmonics the errors are reduced to a minimum.
From what observations are the formulas have been derived?
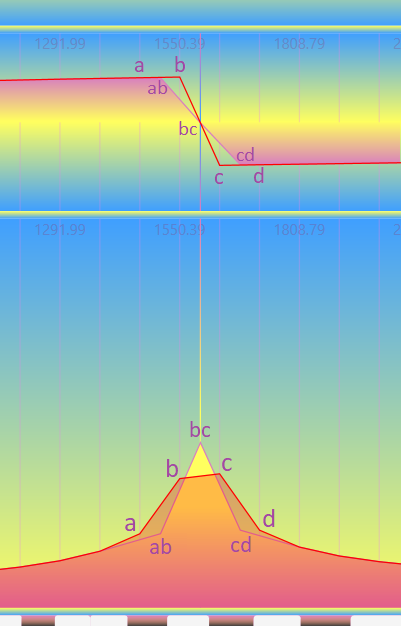
Let consider the magnitude and phase spectrums of a single harmonic when the frequency falls on a division of a discrete lattice and on different parts of the interval between two nearby divisions.
The frequency of the i-th lattice division can be calculated by the following formula
var binToFrequency = sampleRate / frameSize;
var binFrequency = i * binToFrequency;
When a harmonic hits a grating division, a clear peak is observed in the magnitude spectrum, and the effect of spectral leakage is absent, the magnitude values at the remaining divisions are close to zero. The phase value is also determined with high accuracy, however, sharp phase jumps begin to be observed in the phase spectrum.
With a slight frequency shift into the interval between two grating divisions, the magnitude spectrum begins to show the effect of leakage and a characteristic cutoff of the harmonic's peak, which reaches its maximum in the middle of the interval. In this case, an interesting picture is observed in the phase spectrum: the value of the phase of the harmonic now lies on a straight line that connects the values between two nearby divisions of the lattice, and the rest of the phase spectrum forms smooth curves.

Carefully considering of the shift process uncover the following regularity
var halfStepF = (cF - bF) / 2;
var bcMiddleF = (bF + cF) / 2;
var bcOffsetScale = (cM - bM) / (cM + bM);
var bcF = bcMiddleF + bcOffsetScale * halfStepF;Performing substitutions and transformations with simplifications leads to following expressions for calculating the exact harmonic frequency and its phase
var bcF = (bF * bM + cF * cM) / (bM + cM);
var bcP = bP + (bcF - bF) * (cP - bP) / (cF - bF);
/* y(x) = y0 + ( x - x0) * (y1 - y0) / (x1 - x0) */The magnitude value is a bit more difficult to guess, but with a fairly high accuracy it is described by the expression
var bcM = (bM + cM) - (aM + dM) / Pi.Half;It is necessary to mention methods for detecting leaked peaks in a signal for their further interpolation. There are two characteristic features by which a candidate can be identified: a cut peak in the magnitude spectrum and a jump in the phase spectrum. But the combined probabilistic approach is more reliable.
double GetPeakProbabilityByPhase() => Math.Abs(cP - bP) / Pi.Single;
double GetPeakProbabilityByMagnitude()
{
var bcM = (bM + cM) - (aM + dM) / Pi.Half;
return
(aM < bcM && bcM > dM)
&&
(bM * 0.95 < bcM && bcM > cM * 0.95)
? 0.95
: 0.05;
}
var peakProbabilityByPhase = GetPeakProbabilityByPhase();
var peakProbabilityByMagnitude = GetPeakProbabilityByMagnitude();
var peakProbability = peakProbabilityByPhase * peakProbabilityByMagnitude;
if (peakProbabilityByMagnitude > 0.5 && peakProbabilityByPhase < 0.5)
resonances?.Add(i);
if (peakProbability > 0.5)Detection of resonances
It should be noted that pronounced magnitude cutoffs can also occur at resonances, when two or more significant harmonics lie in the same or nearby intervals of the discrete lattice, but in this case the effect of merging two jumps begins to appear on the phase spectrum, which allows to distinguish resonance from the phenomenon of spectral leakage.
In the general case any two harmonics are resonant, just the characteristic effect of beats begins to become most noticeable when their frequencies are close enough.

RIDDLE №3
An interesting observation: the resonance is very similar to the magnitude modulation of a low-frequency signal by a high-frequency one, for example, the resonance of 440 and 444 hertz is similar to a 4 hertz signal (or frequencies of that order) modulated at about 442 hertz. This assumption requires research, clarification and further verification.
At the final stage, after performing the PMI, it is easy to extract pure harmonic components from the spectral data, which already have not a pixel-by-pixel, but a raster representation (frequency/magnitude/phase).
public static IEnumerable<Bin> EnumeratePeaks(this IList<Bin> spectrum, double silenceThreshold = 0.01)
{
var count = spectrum.Count - 3;
for (var i = 0; i < count; i++)
{
spectrum[i + 0].Deconstruct(out var aF, out var aM, out var aP);
spectrum[i + 1].Deconstruct(out var bF, out var bM, out var bP);
spectrum[i + 2].Deconstruct(out var cF, out var cM, out var cP);
if ((aM + cM) * 0.25d < bM && aM < bM && bM > cM && bM > silenceThreshold)
yield return spectrum[i + 1];
}
}The method allows to identify a set of the most pronounced harmonics of the original signal, after which they can be easily represented as complex numbers or cosine waves for further high-precision processing via basic mathematical operations.
In some cases this provides a value information compression of signals due to the loss of insignificant and noise harmonics, which makes it possible to perform further calculations and transformations more compactly and optimally than working with the original raster arrays.
RESULTS
The method of phase-magnitude interpolation opens up new possibilities in the field of processing and compression of signals, since it allows to extract with high accuracy its analog-vector information component from a discrete-raster representation of a signal.
MIRRORS OF THE ARTICLE
EN: makeloft, gitlab, gihub, habr
RU: makeloft, gitlab, gihub, habr
PLAYGROUND