Введение
Я продолжаю серию статей посвящённую тематике pattern recognition, computer vision и machine learning. Сегодня я вам представляю обзор алгоритма, который носит название eigenface.

В основе алгоритма лежит использование фундаментальных статистических характеристик: средних (мат. ожидание) и ковариационной матрицы; использование метода главных компонент. Мы также коснёмся таких понятий линейной алгебры, как собственные значения (eigenvalues) и собственные вектора (eigenvectors) (wiki: ru, eng). И вдобавок, поработаем в многомерном пространстве.
Как бы страшно всё это не звучало, данный алгоритм, пожалуй, является одним из самых простых рассмотренных мною, его реализация не превышает нескольких десятков строк, в тоже время он показывает неплохие результаты в ряде задач.
Для меня eigenface интересен поскольку последние 1.5 года я занимаюсь разработкой, в том числе, статистических алгоритмов обработки различных массивов данных, где очень часто приходится иметь дело со всеми вышеописанными «штуками».
Инструментарий
По сложившейся, в рамках моего скромного опыта, методике, после обдумывания какого-либо алгоритма, но перед его реализацией на С/С++/С#/Python etc., необходимо быстро (насколько это возможно) создать математическую модель и опробовать её, что-нибудь посчитать. Это позволяет внести необходимые коррективы, исправить ошибки, обнаружить то, что не было учтено при размышлении над алгоритмом. Для этого всего я использую MathCAD. Преимущество MathCAD в том, что наряду с огромным количеством встроенных функций и процедур, в нём используется классическая математическая нотация. Грубо говоря, достаточно знать математику и уметь писать формулы.
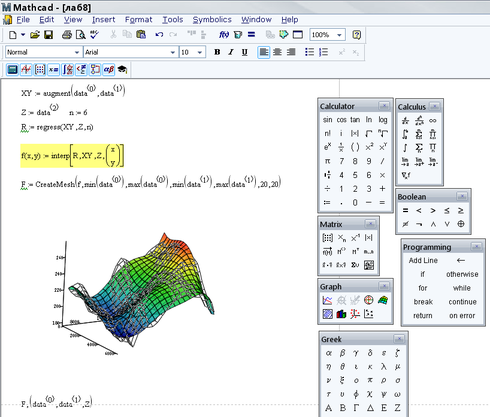
Краткое описание алгоритма
Как и любой алгоритм из серии machine learning, eigenface необходимо сначала обучить, для этого используется обучающая выборка (training set), представляющая собой изображения лиц, которые мы хотим распознать. После того как модель обучена, мы подадим на вход некоторое изображение и в результате получим ответ на вопрос: какому изображению из обучающей выборки с наибольшей вероятностью соответствует пример на входе, либо не соответствует никакому.
Задача алгоритма представить изображение как сумму базисных компонент (изображений):
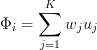
Где Фi – центрированное (т.е. за вычетом среднего) i-ое изображение исходной выборки, wj представляют собой веса и uj собственные вектора (eigenvectors или, в рамках данного алгоритма, eigenfaces).

На рисунке выше мы получаем исходное изображение взвешенным суммированием собственных векторов и прибавлением среднего. Т.е. имея w и u, мы можем восстановить любое исходное изображение.
Обучающую выборку необходимо спроецировать в новое пространство (причём пространство, как правило, гораздо больше размерности, чем исходное 2х мерное изображение), где каждая размерность будет давать определённый вклад в общее представление. Метод главных компонент позволяет найти базис нового пространство таким образом, чтобы данные в нём располагались, в некотором смысле, оптимально. Чтобы понять, просто представьте, что в новом пространстве некоторые размерности (aka главные компоненты или собственные вектора или eigenfaces) будут «нести» больше общей информации, тогда как другие будут нести только специфичную информацию. Как правило, размерности более высокого порядка (отвечающие меньшим собственным значениям) несут гораздо меньше полезной (в нашем случае под полезной понимается нечто, что даёт обобщённое представление о всей выборке) информации, чем первые размерности, соответствующие наибольшим собственным значениям. Оставляя размерности только с полезной информацией, мы получаем пространство признаков, в котором каждое изображение исходной выборки представлено в обобщённом виде. В этом, очень упрощённо, и состоит идея алгоритма.
Далее, имея на руках некоторое изображение, мы можем отобразить его на созданное заранее пространство и определить к какому изображению обучающей выборки наш пример расположен ближе всего. Если он находится на относительно большом расстоянии от всех данных, то это изображение с большое вероятностью вообще не принадлежит нашей базе.
За более подробным описанием я советую обращаться к списку External links википедии.
Небольшое отступление. Метод главных компонент имеет достаточно широкое применение. Например, в своей работе я его использую для выделения в массиве данных компонент определённого масштаба (временного или пространственного), направления или частоты. Он может быть использован как метод для сжатия данных или метод уменьшения исходной размерности многомерной выборки.
Создание модели
Для составления обучающей выборки использовалась Olivetti Research Lab's (ORL) Face Database. Там имеются по 10 фотографий 40 различных людей:

Для описания реализации алгоритма я буду вставлять сюда скриншоты с функциями и выражениями из MathCAD и комментировать их. Поехали.
1.

faceNums задаёт вектор номеров лиц, которые будут использоваться в обучении. varNums задаёт номер варианта (согласно описанию базы у нас 40 директорий в каждой по 10 файлов изображений одного и того же лица). Наша обучающая выборка состоит из 4х изображений.
Далее мы вызываем функцию ReadData. В ней реализуется последовательное чтение данных и перевод изображения в вектор (функция TwoD2OneD):

Таким образом на выходе имеем матрицу Г каждый столбец которой является «развёрнутым» в вектор изображением. Такой вектор можно рассматривать как точку в многомерном пространстве, где размерность определяется количеством пикселей. В нашем случае изображения размером 92х112 дают вектор из 10304 элементов или задают точку в 10304-мерном пространстве.
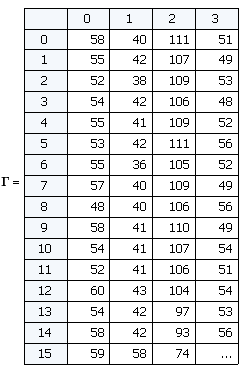
2. Необходимо нормализовать все изображения в обучающей выборке, отняв среднее изображение. Это делается для того, чтобы оставить только уникальную информацию, убрав общие для всех изображений элементы.

Функция AverageImg считает и возвращает вектор средних. Если мы этот вектор «свернём» в изображение, то увидим «усреднённое лицо»:

Функция Normalize вычитает вектор средних из каждого изображения и возвращает усреднённую выборку:

3. Следующий шаг это вычисление собственных векторов (они же eigenfaces) u и весов w для каждого изображения в обучающей выборке. Другими словами, это переход в новое пространство.

Вычисляем ковариационную матрицу, потом находим главные компоненты (они же собственные вектора) и считаем веса. Те, кто познакомятся с алгоритмом ближе, въедут в математику. Функция возвращает матрицу весов, собственные вектора и собственные значения. Это все необходимые для отображения в новое пространство данные. В нашем случае, мы работаем с 4х мерным пространством, по числу элементов в обучающей выборке, остальные 10304 — 4 = 10300 размерности вырождены, мы их не учитываем.
Собственные значения нам, в целом, не нужны, но по ним можно проследить кое-какую полезную информацию. Давайте взглянем на них:

Собственные значения на самом деле показывают дисперсию по каждой из осей главных компонент (каждой компоненте соответствует одна размерность в пространстве). Посмотрите на правое выражение, сумма данного вектора = 1, а каждый элемент показывает вклад в общую дисперсию данных. Мы видим, что 1 и 3 главные компоненты дают в сумме 0.82. Т.е. 1 и 3 размерности содержат 82% всей информации. 2ая размерность свёрнута, а 4ая несёт 18% информации и нам она не нужна.
Распознавание
Модель составлена. Будем тестировать.

Мы создаём новую выборку из 24 элементов. Первые 4ре элемента те же, что и в обучающей выборке. Остальные это разные варианты изображений из обучающей выборки:

Далее загружаем данные и передаём в процедуру Recognize. В ней каждое изображение усредняется, отображается в пространство главных компонент, находятся веса w. После того как вектор w известен необходимо определить к какому из существующих объектов он ближе всего расположен. Для этого используется функция dist (вместо классического евклидова расстояния в задачах распознавания образов лучше применять другую метрику: расстояние Махалонобиса). Находится минимальное расстояние и индекс объекта к которому данное изображение расположено ближе всего.
На выборке из 24 показанных выше объектов эффективность классификатора 100%. Но есть один ньюанс. Если мы подадим на вход изображение, которого нет в исходной базе, то всё равно будет вычислен вектор w и найдено минимальное расстояние. Поэтому вводится критерий O, если минимальное расстояние < O значит изображение принадлежит к классу распознаваемых, если минимальное расстояние > O, то такого изображения в базе нет. Величина данного критерия выбирается эмпирически. Для данной модели я выбрал O = 2.2.
Давайте составим выборку из лиц, которых нет в обучающей и посмотрим насколько эффективно классификатор отсеет ложные образцы.
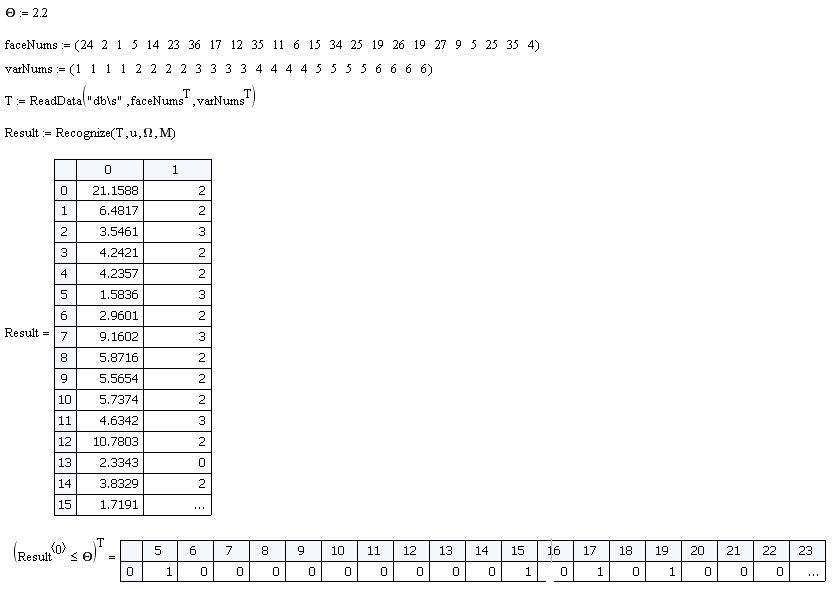
Из 24 образцов имеем 4 ложных срабатывания. Т.е. эффективность составила 83%.
Заключение
В целом простой и оригинальный алгоритм. В очередной раз доказывает, что в пространствах большей размерности «скрыто» множество полезной информации, которая может быть использована различным образом. Вкупе с другими продвинутыми методиками eigenface может применятся с целью повышения эффективности решения поставленных задач.
Например, у нас в качестве классификатора применяется простой distance classifier. Однако мы могли бы применить более совершенный алгоритм классификации, например Support Vector Machine (Метод Опорных Векторов) или нейросеть.
В следующей статьей речь пойдёт о Support Vector Machine (Метод Опорных векторов). Относительно новый и очень интересный алгоритм, во многих задачах может быть использован как альтернатива НС.
При написании статьи использовались материалы:
onionesquereality.wordpress.com
www.cognotics.com
Материалы:
Лист расчётов для MathCAD 14
UPD:
Я вижу многим непонятна и пугает математика. Тут есть два пути.
1. Если вы хотите понять весь смысл всех действий алгоритма, то следует начать с понимания базовых вещей: ков. матрицы, метода главных компонент, значение и смысл собственных векторов и значений. Если вы знаете, что это, то всё становится понятно.
2. Если вы хотите просто реализовать и использовать алгоритм, то берёте качаете лист расчётов для MathCAD'a. Запускаете, смотрите, меняете параметры. Там расчётов на пол экрана и в них нет ничего сложнее умножения матриц (ну если не считать встроенных функций вычисления собственных векторов, но в это вникать не надо). Вот в помощь реализации на python, matlab, C++.