
При написании высокоуровневого кода мы редко задумываемся о том, как реализованы те или иные инструменты, которые мы используем. Ради этого и строится каскад абстракций: находясь на одном его уровне, мы можем уместить задачу в голове целиком и сконцентрироваться на её решении.
И уж конечно, никогда при написании a * b мы не задумываемся о том, как реализовано умножение чисел a и b в нашем языке. Какие вообще есть алгоритмы умножения? Это какая‑то нетривиальная задача?
В этой статье я разберу с нуля несколько основных алгоритмов быстрого умножения целых чисел вместе с математическими приёмами, делающими их возможными.
Оглавление
Многочлены vs преобразование Фурье: алгоритм Шенхаге-Штрассена
• ��ро быстрое преобразование ФурьеМодульная арифметика и второй алгоритм Шенхаге-Штрассена
• Про модульную арифметику чисел
• Про модульную арифметику многочленов
Зачем быстро умножать числа?
Программы постоянно перемножают числа. Перемножения 32-битных, 64-битных, а иногда и более длинных чисел встроены напрямую в арифметико‑логические устройства микропроцессоров; генерация оптимальных цепей для кремния — отдельная инженерная наука. Но не всегда встроенных возможностей хватает.
Например, для криптографии. Криптографические алгоритмы (вроде повсеместно используемого RSA) оперируют числами длиной в тысячи бит. Если мы сводим операции над 4096-битными числами к операциям над 64-битными словами, разница в количестве операций между алгоритмами за и
уже составляет десять раз!
Деление тоже сводится к умножению; в некоторых процессорах даже нет инструкции для целочисленного деления.
Но сразу признаюсь: не все существующие алгоритмы быстрого умножения достаточно практичны для широкого применения — по крайней мере на сегодняшний день. Помимо практического здесь силён академический интерес. Как вообще математически устроена операция умножения? Насколько быстро её можно делать? Можем ли мы найти оптимальный алгоритм и чему научимся в процессе поиска?
Его величество столбик
Когда-то очень давно мне попалось на глаза видео с кричащим названием "How to Multiply", описывающее так называемый японский метод умножения. Что меня удивило — так это то, что метод этот подаётся как более простой и интуитивно понятный. Оказывается, если умножение в столбик делать не в столбик, а занимая половину листа бумаги, получается проще и понятнее!
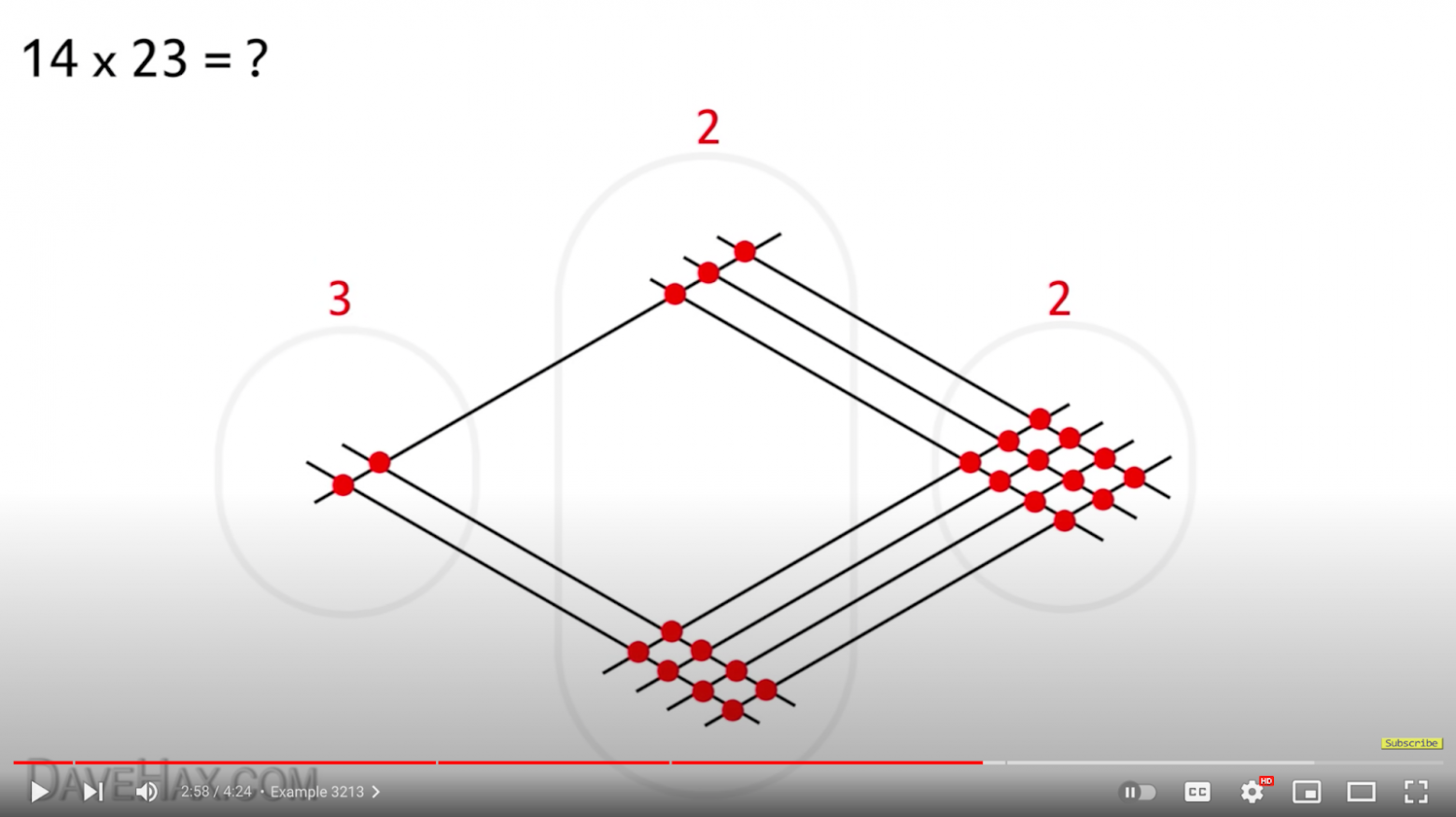
Да-да, принципиально это тот же самый алгоритм умножения столбиком. Можем посмотреть на запись в столбик и сравнить её с картинкой:
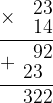
92 — это две больших группы красных точек на нижне-правой диагонали. 23 — две маленьких группы на верхне-левой диагонали. Точно так же, как и в столбике, мы вынуждены перемножить попарно все разряды, потом сложить, и потом сделать перенос. Умножение в столбик — не что иное, как компактный на бумаге и относительно удобный для человеческого сознания способ проделать алгоритм, объединяющий в себе практически все придуманные до XX века способы умножения, за редким исключением вроде умножения египетских дробей.
Асимптотическая сложность умножения в столбик не зависит от того, в какой системе счисления мы производим умножение, и составляет операций, где
и
— количество разрядов в множителях. Каждый из
разрядов одного множителя нужно умножить на каждый из
разрядов второго множителя, после чего получившиеся
маленьких чисел (в каждом не больше двух разрядов) сложить.
Почему асимптотика не зависит от системы счисления?
В разных системах счисления у чисел разное количество разрядов, это верно. Количество десятичных разрядов в числе x равно в двоичной —
(скобки-уголки означают округление вверх). Но мы знаем, что логарифмы по разному основанию связаны друг с другом константным множителем:
А константные множители не имеют значения при анализе асимптотики.
Обычно при анализе сложности под и
подразумевается количество двоичных разрядов, а числа предполагаются примерно одинаковой длины; тогда формула сложности упрощается до
.
Что означает запись O(N²)?
Многих программистов О-нотации учит улица — они сталкиваются с ней сразу в оценке сложности каких-то алгоритмов. Но О-формализм происходит из математического анализа, и у него есть строго определённый смысл, причём не очень хорошо согласующийся с остальными привычными для математики обозначениями.
Если у нас есть функция — в наших примерах это, как правило, будет количество операций, нужных для обработки алгоритмом входных данных в размере
бит — то запись
означает, что существует некоторая константа C такая, что начиная с достаточно больших
То есть функция растёт не быстрее, чем N^2.
При этом сама запись означает класс функций, для которых выполнено это условие. В привычной теоретико-множественной нотации это было бы правильно записать как
— функция входит во множество функций, растущих не быстрее чего-то там.
При этом ничего не сказано о том, может ли функция расти медленнее, чем . Например, в случае алгоритма умножения в столбик мы могли бы без зазрения совести записать
— и формально всё ещё были бы правы. Действительно, операций нужно меньше, чем
. Полезная ли это информация? Не очень.
Соответственно, одна и та же функция может быть «равна» разным ; при этом между друг другом эти
не становятся равны:
Так что обращаться с в выражениях нужно осторожно.
Помимо — наиболее, пожалуй, распространённого среди программистов — есть и другие классы функций с аналогичной записью.
означает, что функция растёт медленее, чем
; да не просто медленнее, а настолько, что их частное становится с ростом
всё ближе и ближе к нулю:
Например, в матанализе постоянно используют запись , чтобы обозначить незначительную величину, стремящееся к нулю. Единица в скобках при этом не имеет какого-то существенного значения — там могла бы быть любая константа; можете написать
и формально это будет верно. Иногда бывает важно указать, с какой именно скоростью величина стремится к нулю. Тогда пишут
,
и так далее.
Другая встречающаяся нотация означает, что функция растёт точно со скоростью
, то есть существуют константы
и
такие, что начиная с достаточно больших
Помимо простого использования со знаком равенства, как в примерах выше, классы функций можно использовать в арифметических операциях. Например, запись
означает, что функция равна плюс нечто маленькое, стремящееся к нулю при росте
. В отличие от
или
, эта запись не допускает произвольных множителей при
— ровно
и всё тут.
Работает (при некоторых ограничениях) и привычная арифметика в равенствах. Так, если , обе части равенства можно поделить, например, на константу:
съедает любые константы, поэтому справа ничего не изменилось. А можно поделить на
:
Не-константу нельзя просто выкинуть, поэтому она ушла внутрь и сократилась с тем, что там было.
Разделяй и властвуй: алгоритм Карацубы
Первый шаг на пути ускорения умножения совершил в 1960-м году советский математик Анатолий Карацуба. Он заметил, что если длинные числа поделить на две части:
То можно обойтись тремя умножениями этих более коротких частей друг на друга, а не четырьмя, как можно было бы подумать. Вместо прямого подсчёта , требующего двух умножений, достаточно посчитать
и вычесть из результата числа
и
, нужные нам в любом случае для получения младших и старших разрядов.
После этих расчётов остаётся лишь пробежаться по разрядом справа налево и провести суммирование:
По сравнению с умножениями это быстрая операция, не заслуживающая особого внимания — как и два лишних сложения в скобках.
Для построения эффективного алгоритма осталось превратить это наблюдение в рекурсивную процедуру. Половинки чисел тоже будем делить на половинки и так далее, пока не дойдём до достаточно коротких чисел, которые можно перемножить в столбик или, допустим, через lookup table.
Поскольку мы каждый раз делим задачу на три задачи с вдвое меньшими (по количеству бит) числами, для перемножения двух чисел длины нам потребуется рекурсия глубины
и суммарно
умножений чисел наименьшей длины; отсюда получаем оценку сложности в
Занятный факт — аналогичные фокусы с экономией за счёт одновременных умножений используются ещё в ряде мест. Так, два комплексных числа
и
также можно перемножить за три вещественных умножения вместо четырёх, вычислив
,
и
. А алгоритм Пана для быстрого перемножения матриц основывается на ��ом, что можно одновременно вычислить произведения двух пар матриц
и
за меньшее число умножений, чем по отдельности [1, 2]. Не говоря уж о том, что само по себе перемножение матриц быстрее, чем за
— это быстрое одновременное умножение матрицы на
векторов.
Числа vs многочлены: алгоритмы Тоома-Кука
При виде магического сокращения вычислительной сложности при разбиении множителей на две части как-то сам собой возникает вопрос: а можно разбить множители на бóльшее число частей и получить бóльшую экономию?
Ответ — да; и подход, позволяющий это сделать, включает в себя алгоритм Карацубы как частный случай. Но для его формулировки нам придётся проделать некий фокус.
Давайте попробуем разбить те же самые числа на три части:
Если мы внимательно посмотрим на коэффициенты при степенях десятки, которые возникают при перемножении этих скобок:
То (при наличии опыта в алгебре) заметим, что где-то мы такое уже видели. При перемножении многочленов!
Если взять части наших чисел a и b и объявить их коэффициентами многочленов и
при соответствующих степенях, числа в таблице выше будут не чем иным, как коэффициентами многочлена
:
Сами же числа получаются из многочленов путём вычисления значения в некоторой точке. Какой именно — зависит от системы счисления и размера частей:
Хорошо, свели одну задачу к другой. В чём преимущество многочленов? Помимо того, что это некоторые формальные конструкции с параметрами, это также функции; чтобы вычислить в произвольной точке, не нужно перемножать многочлены — достаточно вычислить оба значения в этой точке и перемножить их. Если бы я писал продакшн-код, в котором по какой-то причине нужно перемножать многочлены, я бы и вовсе сделал перемножение ленивым.
Но нам не нужно вычислять значение в точке. Нам нужны коэффициенты. А коэфф��циенты многочлена можно восстановить по значениям в точках, решив систему линейных уравнений:
Здесь — это точки, в которых нам известны значения многочлена, в правой части — сами эти значения, а
— неизвестные нам коэффициенты многочлена. Количество неизвестных соответствует степени многочлена + 1; чтобы решение было единственным, нужно, соответственно, знать значения в таком же количестве точек. В нашем примере это пять точек, потому что у многочлена-произведения степень 4:
Если переписать эту систему уравнений в матричном виде, получим
Соответственно, для создания алгоритма быстрого умножения чисел нам достаточно:
выбрать, на сколько частей мы разбиваем числа (можно даже разбить
и
на разное количество частей);
выбрать точки
, в которых мы будем вычислять значения многочленов;
построить по ним матрицу Вандермонда;
вычислить её обратную матрицу.
В ходе алгоритма нам нужно будет два раза умножить на прямую матрицу (по разу для каждого из чисел, которые мы хотим перемножить), перемножить результаты алгоритмом умножения чисел меньшего размера, и один раз умножить получившийся вектор на обратную матрицу.
Давайте посмотрим на матрицу для точек :
from sympy import Rational
from sympy.matrices import Matrix
# Точки, в которых будем вычислять значения многочленов:
x = [0, 1, -1, 2, -2]
# Матрица Вандермонда, построенная по этим точкам:
v = Matrix([
[
Rational(x_i ** j )
for j, _ in enumerate(x)
] for x_i in x
])(Серым я отметил числа, не имеющие значения, поскольку соответствующие коэффициенты в многочленах-множителях заведомо равны нулю.)
И на её обратную:
За исключением некоторой проблемы с делением на 3, подавляющая часть вычислений здесь представляется битовыми сдвигами, сложениями и вычитаниями «коротких» чисел, а это операции «простые» — имеющие линейную сложность.
Как проанализировать итоговую сложность получившегося алгоритма? Давайте обозначим количество операций через , где
— количество бит в наших множителях, и выведем рекуррентную формулу:
Что здесь написано: умножение двух чисел длиной бит мы умеем сводить к 5 умножениям чисел длиной
бит и ещё какому-то количеству простых операций над числами длиной
бит. Применяем основную теорему о рекуррентных соотношениях и получаем итоговую сложность
Таким образом мы ускорили умножение с до
.
Алгоритмы, получаемые таким образом, называются алгоритмами Тоома-Кука. Они активно используются на практике; в одной только библиотеке GMP поддержано 13 разных вариантов разбиения чисел.
Закономерный следующий вопрос: что дальше? Если число бьётся на частей, сложность получается
Показатель степени при большом можно упростить:
Получается, мы можем построить алгоритм со сколь угодно близкой к 1 степенью в асимптотике? Увы, тут есть сложности.
Во-первых, это непрактично. Логарифм возрастает крайне медленно; асимптотика, соответственно, тоже будет падать медленно, а константа при этом будет быстро расти, потому что числа в матрицах будут всё больше и разнообразнее.
Во-вторых, это неинтересно. Да-да! Дальше мы будем обсуждать алгоритмы, сложность которых лучше, каким маленьким бы ни было
.
Занятный факт — аналогичной методу Тоома-Кука техникой строятся быстрые алгоритмы перемножения матриц. Однако процедура перемножения матриц по своей математической природе оказалась намного сложнее перемножения многочленов; поэтому до сих пор нет уверенности, что можно перемножать матрицы за
для сколь угодно малого
. Лучшая асимптотика на сегодняшний день составляет примерно
.
Многочлены vs преобразование Фурье: алгоритм Шенхаге-Штрассена
Раз рекуррентное деление на несколько частей нам не интересно, давайте попробуем сделать радикальный шаг. Что, если делить числа не на фиксированное количество частей, а на части фиксированной длины?
Например, на десятичные разряды. В таком случае нам нужно будет точек для
-разрядного числа; в остальном подход как будто бы тот же самый, что в предыдущем разделе. Что ж, давайте возьмём
и проведём численный эксперимент, чтобы убедиться, что всё работает!
import math
import numpy as np
# Числа, которые мы изначально собирались перемножить:
a = 235739098113
b = 187129102983
m = len(str(a))
# Коэффициенты соответствующих многочленов в порядке
# возрастания степени. Поскольку результирующий многочлен
# будет степени 2*m-1, добиваем нулями до нужной ширины:
a_coefs = [int(a_i) for a_i in str(a)[::-1]] + [0] * (m - 1)
b_coefs = [int(b_i) for b_i in str(b)[::-1]] + [0] * (m - 1)
n = len(a_coefs)
# Точки, в которых будем вычислять значения многочленов:
x = np.arange(n)
# Матрица Вандермонда, построенная по этим точкам:
v = np.vander(x, increasing=True)
# Вычисление значения многочлена в точке — не что иное, как
# умножение этой матрицы на вектор коэффициентов:
a_y = v @ a_coefs
b_y = v @ b_coefs
# Поточечно перемножаем значения, чтобы получить
# значения многочлена-произведения:
c_y = a_y * b_y
# Восстанавливаем коэффициенты многочлена-произведения:
c_coefs = np.linalg.solve(v, c_y)
# Для сверки считаем коэффициенты "в лоб":
actual_c_coefs = [
sum(a_coefs[j] * b_coefs[i-j] for j in range(i+1))
for i in range(n)
]
# Считаем длину вектора-разности и делим на длину настоящего,
# чтобы получить относительную погрешность:
print(np.linalg.norm(c_coefs - actual_c_coefs) /
np.linalg.norm(actual_c_coefs))Запускаем и…
2.777342817120168e+17Хо-хо, да это не просто мимо, это фантастически мимо! Но почему?
Оказывается [3], у матриц Вандермонда есть неприятное свойство — решать системы с ними в подавляющим большинстве случаев очень плохая идея, потому что погрешность результата растёт экспоненциально с размером матрицы. Можно улучшить ситуацию, взяв вместо комплексные точки на единичной окружности:
x = np.exp(1j * np.random.uniform(0, math.pi, size=n))
...
0.00015636299542432733Но лучшим выбором оказывается взять точки, равномерно распределённые на единичной окружности и являющиеся корнями из единицы степени .
x = np.exp(-1j * np.linspace(0, 2*math.pi, n, endpoint=False))Что ещё за корни из единицы?
Хотя в привычной нам вещественной арифметике равенство выполнено только при
, на комплексной плоскости всё гораздо веселее. У каждого многочлена степени
есть ровно
комплексных корней, и многочлена
это правило (также известное как основная теорема алгебры) тоже касается.
Корнями из единицы степени являются числа на комплексной плоскости, расположенные в вершинах правильного
-угольника, вписанного в единичную окружность:

Поскольку при умножении комплексных чисел их модули перемножаются (а у всех корней из единицы модуль равен единице — они же на единичной окружности), а фазы складываются, при возведении числа в последовательные степени мы получим по очереди все корни из единицы. За это свойство
называется первообразным корнем из единицы.
Запускаем новый вариант кода и получаем
1.5964929527133826e-15Отлично! Мы дошли до предела машинной точности.
Но самое изумительное — при таком выборе иксов матрица представляет собой не что иное, как матрицу дискретного преобразования Фурье! А значит, мы можем умножать векторы на эту матрицу и решать систему уравнений с ней алгоритмом быстрого преобразования Фурье за операций сложения и умножения — вместо наивного алгоритма за
.
Что такое дискретное преобразование Фурье?
Преобразование Фурье досталось нам из высшей математики и волновой физики. В физике оно известно как способ разложить сигнал (например, аудио) какой-то произвольной формы

на сумму элементарных сигналов — гармоник с длиной волны, кратной ширине отрезка:
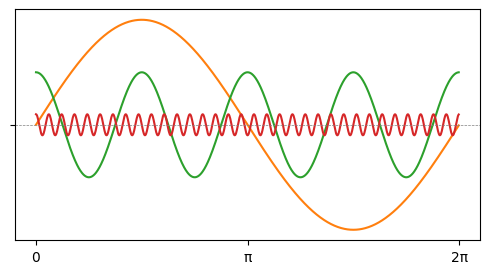
Одна гармоника соответствует постоянному звуку некой фиксированной частоты и громкости; сумма гармоник может дать любую мелодию. Сколь угодно сложный сигнал можно разложить на гармоники, если взять их достаточно много. Совокупность гармоник (частоты + амплитуды) называется спектром сигнала.
Преобразование Фурье — построение в первую очередь теоретическое; Жозеф Фурье открыл его задолго до появления компьютеров. На практике мы не можем оперировать сигналами как функциями; у нас есть только дискретизации, замеры значения сигнала с каким-то шагом по времени.
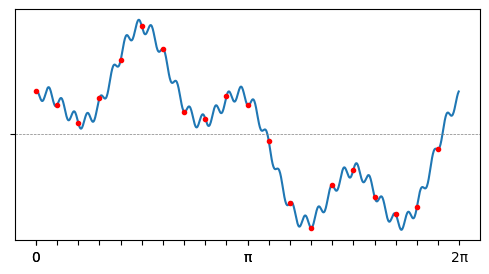
Согласно теореме Котельникова-Найквиста-Шеннона при такой ограниченной информации мы всё ещё можем восстановить гармоники (а с ними — и весь сигнал), если предположим, что сигнал был достаточно простым (в нём не было каких-то сверхвысоких частот). Этим и занимается дискретное преобразование Фурье — фактически это матрица, которую нужно умножить на вектор со значениями дискретизированного сигнала, чтобы получить вектор с амплитудами, соответствующими разным частотам гармоник.
Так, дискретизация на картинке выше недостаточно частая, чтобы восстановить самую высокую частоту:
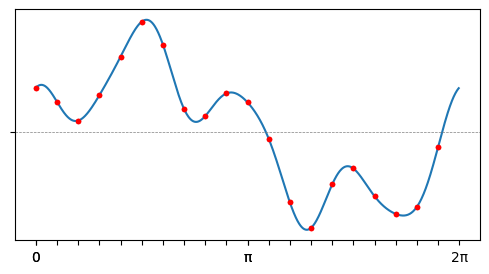
А более частая, удовлетворяющая условию теоремы — достаточна:

По роковому стечению обстоятельств матрица дискретного преобразования Фурье является матрицей Вандермонда, построенной по корням из единицы.
В целом анализ Фурье — очень интересный раздел математики, связывающий воедино множество ранее разобщённых концепций. Его подробное описание, конечно, уходит совсем далеко за рамки статьи; можно начать со статей на Хабре «Простыми словами о преобразовании Фурье» и «Преобразование Фурье в действии: точное определение частоты сигнала и выделение нот».
Что такое быстрое преобразование Фурье?
Дискретное преобразование Фурье применяется повсеместно для обработки сигналов (например, шумоподавления), часто реализуется аппаратно и встречается с совершенно неожиданных устройствах (например, МРТ-сканерах [4]). Это создаёт потребность в создании настолько быстрого алгоритма, насколько возможно.
Умножение на матрицу «в лоб» стоит — это считается довольно медленным в практических алгоритмах. Быстрое преобразование Фурье — название семейства алгоритмов, достигающих асимптотики
за счёт сведения задачи к нескольким задачам меньшего размера с линейной стоимостью одного шага рекурсии. Самый простой вариант — алгоритм для
, сводящий задачу к двум задачам размера
; рекурсия глубины
приводит к общей сложности
.
Про него в интернете, конечно, написано много материалов разной степени читабельности. Но давайте я попробую очень быстро на пальцах показать, за счёт чего вычисление можно ускорить до .
Дискретное преобразование Фурье и обратное дискретное преобразование Фурье — восстановление сигнала по спектру — очень похожи математически, и алгоритм почти идентичный; объяснить его будет проще на примере обратного преобразования.
Обратное преобразование заключается в том, что нужно взять гармоник, у которых мы знаем частоту и амплитуду, посчитать их значения в
точках отрезка
и сложить, получив вектор из
значений сигнала-суммы гармоник. На рисунке пример для
:
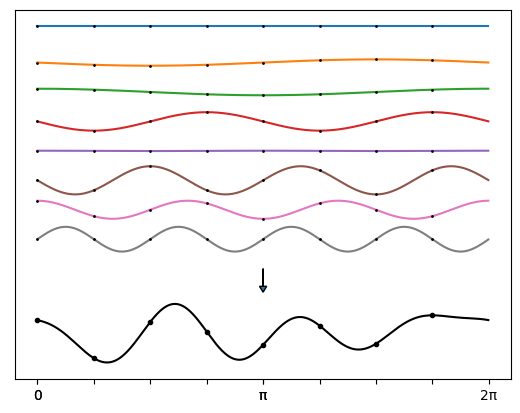
Поделив отрезок пополам, можно заметить, что гармоники делятся на два типа:
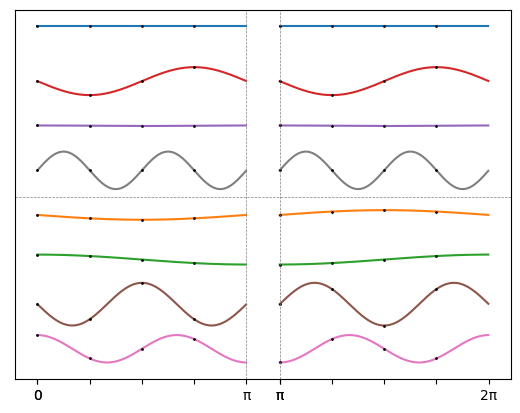
В верхней части — кривые, половинки которых одинаковы в первой и второй половине отрезка; в нижней — выглядящие вертикально отражёнными, то есть одна половина получается из другой умножением на . А значит, можно сэкономить, вычисляя значения всех гармоник только на половине отрезка!
При этом задача для произвольной гармоники на половине отрезка соответствует задаче для гармоники с вдвое меньшей частотой и точек:
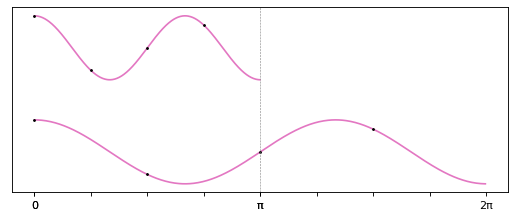
Получается, что для решения исходной задачи восстановления сигнала в точках по данным
гармоникам нам достаточно:
просуммировать
гармоник первого типа (взяв вдвое меньшую частоту) в
точках;
просуммировать
гармоник второго типа (также взяв вдвое меньшую частоту) в
точках;
первую сумму — вектор длины
— повторить два раза, получив вектор длины
;
вторую сумму — также вектор длины
— тоже повторить два раза, но второй раз — со знаком минус;
два получившихся вектора сложить.
Поскольку мы свели задачу для к двум задачам для
и дополнительным шагом обработки стоимостью
, итоговая сложность получается равной
.
Так мы и получили предельно простой пересказ алгоритма Кули-Тьюки!
Делить числа на части по десятичным разрядам — это, конечно, не самый эффективный способ. Тут даже нет как таковой рекурсии — после первого разделения на части мы сразу приходим к числам от 0 до 9, которые можно перемножить по таблице умножения. Наилучшая асимптотика в таком алгоритме получается, если делить -битные числа на части длиной примерно
бит.
Полностью алгоритм Шенхаге-Штрассена выглядит так.
Берём на вход два числа, которые хотим перемножить; числа эти длины
бит. На практике это значит, что бóльшее из чисел имеет
бит.
Делим двоичную запись чисел на фрагменты, каждый длиной примерно
бит:
Эти фрагменты — целые числа с
бит — объявляем коэффициентами многочленов, которые нужно перемножить:
Теперь у нас на руках два вектора коэффициентов многочленов. К этим векторам применяем дискретное преобразование Фурье:
Для этого нам потребуются вычисления с плавающей точкой, гарантирующие достаточно точный результат — на это потребуется порядкабит. Умножения делаем рекурсивно этим же алгоритмом.
Полученные векторы перемножаем поэлементно. Для перемножения элементов также используем рекурсивно этот алгоритм (или простые алгоритмы, если числа уже достаточно маленькие). Рекурсия будет очень небольшой глубины, потому что на каждом шаге мы от входных данных размера
переходим к
; например, для чисел, занимающих гигабайт (!) каждое, глубина рекурсии будет всего 6.
К получившемуся вектору применяем обратное преобразование Фурье. Умножения делаем рекурсивно этим же алгоритмом.
Наконец, из получившегося вектора коэффициентов многочлена-произведения восстанавливаем число-результат умножения, суммируя в столбик справа налево.
Формула асимптотической сложности получившегося алгоритма довольно страшная, в целом асимптотика получается чуть-чуть хуже . Но можно оценить полёт мысли и количество математических конструкций, требующихся для достижения такого результата.
Модульная арифметика и второй алгоритм Шенхаге-Штрассена
Хотя первый алгоритм Шенхаге-Штрассена круто улучшает асимптотику по сравнению с ранее существовавшими методами, у него всё ещё есть зоны роста. Во-первых, на каждом шаге рекурсии происходит экспоненциальное уменьшение размеров чисел — с до
. Из-за этого глубина рекурсии очень мала и воспользоваться ускорением получается не в полном объёме. Во-вторых, необходимость производить расчёты с плавающей точкой разной точности весьма непрактична — мы все привыкли к float и double, а реализация чисел с плавающей точкой настраиваемой ширины весьма нетривиальна. (Здесь читатель может возразить, что многое из вышеописанного было нетривиально. Могу только согласиться.)
Второй алгоритм Шенхаге-Штрассена лишён этих двух недостатков, более быстр и в теории, и в практике и наиболее широко используется — например, в библиотеке GMP.
Для решения первой проблемы давайте попробуем разбить числа на более крупные фрагменты — например, размера вместо
. Здесь мы незамедлительно столкнёмся с проблемой: для дискретного преобразования Фурье в таком случае потребуется
операций умножения чисел из
бит; каждое такое умножение будет стоить в лучшем случае
(напомню, все алгоритмы выше стоили ещё дороже), что даёт нам суммарную сложность не меньше
, что уже хуже предыдущего алгоритма. Что-то здесь нужно ускорить.
Для решения второй проблемы можно вспомнить, что в модульной арифметике тоже можно делать быстрое преобразование Фурье. Тогда мы будем иметь дело только с целыми числами! А если подобрать в качестве элементов матрицы Фурье степени двойки, то на них можно будет умножать быстрее, чем за . В идеале вообще за
, потому что умножение на степень двойки — это просто битовый сдвиг.
Что такое модульная арифметика?
Арифметика по модулю — это ровно то, о чём можно подумать из названия. Привычные арифметические операции (сложение, вычитание, умножение) берутся с единственным изменением — после проведения операции надо взять остаток от деления результата на некое фиксированное число p. Так, в арифметике по модулю 7 имеем ,
, но
,
. Принято писать
Арифметика по модулю нам, программистам, очень близка. Если вы оперируете 32-битными (или 64-битными) беззнаковыми целыми числами в своём коде, вы фактически делаете все операции в арифметике по модулю (или, соответственно,
).
Примечательный факт в том, что при таком определении арифметических операций мы получаем полноценную арифметику, в которой сохраняется большинство свойств, к которым мы привыкли в обычной арифметике. Но, конечно, есть нюансы.
Множество чисел в арифметике по модулю p называется кольцом вычетов по модулю и обозначается
; в Серьёзных Книгах также можно встретить запись
. В нём содержатся числа
Само число p в арифметике по модулю эквивалентно нулю (таков остаток от деления на само себя);
эквивалентно 1 и так далее. Отрицательные числа работают по схеме, привычной программистам:
эквивалентно
,
эквивалентно
и так далее.
Деление в модульной арифметике — это первый нюанс. В нет дробей; как определить частное двух чисел, не делящихся друг на друга? По определению деления
— это такое число, что
. Возвращаясь к примерам в арифметике по модулю 7, из равенства
получаем
Однако не всегда в модульной арифметике возможно поделить два числа друг на друга. Это второй нюанс — произведение двух ненулевых чисел в модульной арифметике может быть равно нулю! Так, в арифметике по модулю 6 имеем . Такие числа называются делителями нуля и делить на них не получится. Само существование
и
в арифметике по модулю 6 противоречило бы некоторым аксиомам; это всё равно, что делить на ноль. На практике мы можем легко проверить перебором, что подходящих на роль частного чисел не существует:
Z_6 = range(6)
[(x * 2) % 6 for x in Z_6]
# [0, 2, 4, 0, 2, 4] — нет единицы
[(x * 3) % 6 for x in Z_6]
# [0, 3, 0, 3, 0, 3] — нет единицыМножество чисел, не являющихся делителями нуля, называется мультипликативной группой кольца вычетов по модулю p и обозначается . Например, в случае
имеем
— ведь как мы выяснили только что, 2 и 3 являются делителями нуля; кратная двойке четвёрка — тоже: .
Примечательный факт про мультипликативную группу — любые два числа в ней можно умножать и делить друг на друга, и снова получать элементы из этой группы. Так, .
Если основание арифметики — простое число, делителей нуля в ней не существует и можно делить друг на друга любые числа. Соответственно, в мультипликативной группе в этом случае содержатся все числа из , кроме нуля:
Как находить частное двух чисел на практике, кроме как перебором? Занимательный факт из алгебры: если в мультипликативной группе элементов, то любой её элемент в степени
равен единице. Давайте проверим на паре примеров:
Z_7_mul = range(1, 7)
[pow(x, 6, 7) for x in Z_7_mul]
# [1, 1, 1, 1, 1, 1]
Z_8_mul = [1, 3, 5, 7]
[pow(x, 4, 8) for x in Z_8_mul]
# [1, 1, 1, 1]А это значит, что
и, соответственно, . Возвести число в
-ю степень можно за
умножений алгоритмом быстрого возведения в степень.
Отсюда нюанс третий — в мультипликативной группе все числа являются корнями из единицы степени ! Эти корни при правильном обращении ведут себя аналогично корням из единицы в комплексной арифметике, и для них тоже можно построить алгоритм быстрого преобразования Фурье.
Наблюдение первое: самая удобная арифметика
Для того, чтобы быстро делать умножения во время быстрого преобразования Фурье, нам нужно, чтобы некие числа сочетали два свойства: были степенями двойки — чтобы можно было быстро на них умножать, и были корнями из единицы — чтобы быстрое преобразование Фурье в принципе работало. Значит, привычная всем программистам n-битная арифметика не подходит — потому что это фактически вычисления по модулю , а значит, любая степень двойки при возведении в достаточно большую степень обращается в ноль и никак не может быть корнем из единицы:
num_bits = 5
[pow(2, i, 2**num_bits) for i in range(2*num_bits)]
# [1, 2, 4, 8, 16, 0, 0, 0, 0, 0]Если же основание арифметики кратно двум, но не степени двойки, мы не получим ноль, но и никогда не получим единицу:
mod = 6
[pow(2, i, mod) for i in range(2*mod)]
# [1, 2, 4, 2, 4, 2, 4, 2, 4, 2, 4, 2]Потому что двойка является делителем нуля (в примере выше её можно умножить на три и получить 0 по модулю 6) и не является членом мультипликативной группы.
Гораздо лучше дела обстоят с основаниями, взаимно простыми с двойкой:
mod = 5
[pow(2, i, mod) for i in range(2*mod)]
# [1, 2, 4, 3, 1, 2, 4, 3, 1, 2]Поскольку в этом случае двойка состоит в мультипликативной группе, всегда есть степень, в которую её можно возвести, чтобы получить 1 — и это справедливо также для любой степени двойки. У нас есть неограниченный запас простых чисел, мы могли бы просчитать их наперёд с запасом и делать вычисления по модулю достаточно большого простого числа… Но умножать числа по произвольному модулю быстро не получится даже на степень двойки, потому что после битового сдвига нужно брать остаток от деления, а это медленно.
Время для первого наблюдения — идеально для наших нужд подходит арифметика по модулю . Это число гарантированно взаимно простое с двойкой (потому что нечётное), и по нему легко брать остаток от деления. Как?
Допустим, мы умножили некое число x на некую степень двойки , сделав битовый сдвиг. Если результат уместился в первые n бит, всё отлично. Если результат равен
, тоже неплохо. Если больше — то есть случилось переполнение — все биты, начиная с
-го, надо обнулить. И для этого есть простой алгоритм!
В вычислениях по модулю имеем
. Домножая равенство на
, получим
. Соответственно, каждый лишний
-й бит мы можем превратить в вычитание
-го бита. Собираем по битам число, которое надо вычесть, и вычитаем по модулю — эта операция стоит
. Et voilà!
И дополнительный приятный факт: . Двойка является корнем из единицы заведомо известной нам степени
.
Что там с асимптотикой?
Окей, мы решили, что сводим задачу умножения длинных чисел к нескольким задачам умножения чисел по модулю посредством быстрого преобразования Фурье. Более формально, если на входе у нас были числа длиной
бит, мы делим их на
частей по
бит,
, по уже хорошо знакомой нам процедуре:
Дальше снова превращаем их в многочлены степени :
Коэффициенты этих многочленов рассматриваем в арифметике по модулю , где
— количество бит, способное вместить сумму
произведений двух чисел длины
бит, чтобы не было переполнения. Именно таким может быть самый большой коэффициент в произведении этих двух многочленов:
Мы уже знаем, что можно свести умножение таких многочленов к умножению чисел в
посредством быстрого преобразования Фурье; эти умножения поменьше легко можно провести этим же алгоритмом, а взять потом остаток от деления на
, как мы уже выяснили, можно легко и быстро. Само сведение — быстрое преобразование Фурье в модульной арифметике с быстрыми корнями из единицы — обойдётся нам в
сложений и умножений стоимости
, то есть суммарно
битовых операций. Итого сложность
совершения умножения имеет вид
Насколько крутое ускорение мы можем получить? Сейчас я проведу сильно упрощённый анализ «на пальцах»; более строгий можно глянуть, например, в [5].
Если выбрать и учесть, что
очень мало по сравнению с
, имеем
Сделав замену , получим более простую для анализа формулу:

Так, рекуррентное соотношение. От бит переходим к
, потом к
, потом к
и так далее. Раскрывая
раз, получаем
убывает очень быстро, и как только мы дойдём до какого-то достаточно малого числа, рекурсия остановится. Какая будет глубина рекурсии? Можем заметить, что на
-м шаге длина чисел, с которыми мы имеем дело, имеет вид
Соответственно, решая уравнение , получаем глубину рекурсии
. Складывая степени двойки от нулевой до
(в равенстве выше они умножаются на const), получаем
и суммарную сложность
И это медленно! В первом алгоритме Шенхаге-Штрассена мы уже добились сложности чуть хуже . Нужно ускорить ещё.
Наблюдение второе: самые короткие многочлены
В выражении, оценивающем сложность
можно заметить, что основной вклад в слишком большой результат вносят множители-степени двойки. Они там потому, что разбивая число на частей, мы сводим задачу к
умножений. Это нужно, потому что при умножении двух
-битных чисел получается
-битное число.
Но нам не нужно -битное число. Как только мы сделали первый шаг рекурсии, все вычисления у нас происходят по модулю
. А при вычислениях по модулю длина чисел не может изменяться! Можно ли как-то вместо удвоения длины и взятия остатка от деления обойтись расчётами на
битах?
Если мы хотим при этом сохранить преимущества быстрого преобразования Фурье, от перемножения многочленов мы отказаться не можем. Есть ли в мире многочленов что-то, похожее на арифметику по модулю? Есть!
Арифметика многочленов по модулю???
В жизни нужно довольно рано свернуть не туда, чтобы заработать опыт в арифметике многочленов. Но ничего страшного в ней нет; связь между многочленами и числами, которую мы используем для построения быстрых алгоритмов умножения, также делает арифметику многочленов довольно похожей на привычную.
Складывать и умножать многочлены мы уже умеем — там всё очевидно. Менее очевидно, что многочлены также можно друг на друга делить с остатком — причём это можно делать вот прямо в столбик, как обычные целые числа.

Можем быстро проверить в SymPy, что всё правильно:
import sympy
x = sympy.Symbol("x")
f = 5*x**5 + 4*x**4 + 3*x**3 + 2*x**2 + x
g = x**2 + 2*x + 3
sympy.div(f, g, domain="Q")
# (5*x**3 - 6*x**2 + 20, -39*x - 60)Как только есть деление с остатком, можно ввести арифметику по модулю; основанием такой модульной арифметики, соответственно, будет уже не число , а многочлен
. Подобно тому, как мы строим модульную арифметику, объявляя, что теперь число
эквивалентно нулю, здесь мы объявляем, что многочлен
эквивалентен нулю. Многочлен
становится эквивалентен
,
— многочлену
и так далее.

Всё это продолжает работать, если мы меняем арифметику коэффициентов многочленов, заменяя привычные нам целые или вещественные числа на арифметику по модулю . Выстраивается каскад абстракций: многочлен — это сумма степеней икса с коэффициентами из некоторого множества; неважно, какого именно — главное, чтобы мы эти коэффициенты могли складывать, умножать и (иногда) делить. Этого достаточно, чтобы определить сложение, умножение и деление для самих многочленов, в том числе по модулю
. Коэффициенты при этом живут своей независимой жизнью.
При обычном перемножении многочленов коэффициент при соответствует битам произведения чисел, начиная с
-го. Если же мы делаем расчёты по модулю
, коэффициент при
становится эквивалентен нулевому коэффициенту (при
) со знаком минус:
А в задаче умножения по модулю
-й бит… тоже соответствует нулевому биту со знаком минус!
Это и есть наше ключевое второе наблюдение: перемножение многочленов по модулю эквивалентно перемножению чисел по модулю
.
Теперь у нашего многочлена-произведения есть только значащих коэффициентов. Но есть нюанс: как только мы начинаем рассматривать многочлены по модулю, фраза значение многочлена в точке
теряет смысл. Многочлен в арифметике по модулю
— это не конкретная функция
, а совокупность функций вида
Коэффициенты могут быть произвольными, и могут изменять значения многочлена в разных точках.
Мы можем быстренько провести вычислительный эксперимент, чтобы проверить, насколько хорошо заработает наш проверенный подход с матрицей Вандермонда, если мы попытаемся перемножать многочлены по модулю, просто урезав длину вектора коэффициентов. Попробуем взять разные наборы точек и посмотрим, что будет.
# Будем делить числа на 4 куска по 2 бита.
m = 4
n_ = 4 # n' с запасом
# Основание арифметики коэффициентов:
mod = 2**n_ + 1 # 17
# Два 8-битных множителя:
a_coefs = [0b01, 0b01, 0b10, 0b01] # 101
b_coefs = [0b01, 0b11, 0b00, 0b01] # 77
def construct_vandermonde_matrix_and_inverse(xs: List[int]):
# Строим матрицу Вандермонда "в лоб",
# потому что нам нужна модульная арифметика:
v = np.array([
[pow(xs[i], j, mod) for j in range(m)]
for i in range(m)
])
# Дальше хитрый фокус, чтобы обратить матрицу
# в модульной арифметике. Да, мне было лень писать
# метод Гаусса или конвертировать матрицу из sympy.
det = int(round(np.linalg.det(v)))
det_inv = pow(det, mod - 2, mod)
v_inv_real = np.linalg.inv(v) * det * det_inv
v_inv = np.array(np.round(v_inv_real), dtype=int) % mod
# Проверяем, что действительно получилась
# обратная матрица в модульной арифметике:
assert np.all((v @ v_inv) % mod == np.eye(m, dtype=int))
return v, v_inv
# Перебираем разные наборы точек:
for xs in [
[2, 8, 15, 9],
[2, 4, 8, 16],
[3, 5, 7, 11],
[5, 7, 11, 13],
]:
v, v_inv = construct_vandermonde_matrix_and_inverse(xs)
a_y = (v @ a_coefs) % mod
b_y = (v @ b_coefs) % mod
c_y = (a_y * b_y) % mod
c_coefs = (v_inv @ c_y) % mod
print(c_coefs)
# [14 2 4 8]
# [ 2 10 4 16]
# [ 4 4 0 8]
# [ 0 6 4 13]В зависимости от выбранных точек получаем разные коэффициенты произведения! Но, в отличие от прошлого раза, теперь дело заведомо не в вычислительной погрешности — уж перемножать целые числа мы умеем точно.
Дело как раз в том, что мы никак не учли здесь, что мы умножаем по модулю . Как это учесть?
Посмотрим ещё раз на многочлен по модулю:
На самом деле есть несколько точек, в которых фраза значение многочлена в точке не бессмысленна. Эти точки — корни многочлена ! В этих точках «произвольная» часть этой обобщённой функции всегда обращается в ноль, благодаря чему значение фиксируется.
Какие это точки в примере выше?
def xmp1(x):
return (pow(x, m, mod) + 1) % mod
{i: xmp1(i) for i in range(mod)}
# { 0: 1,
# 1: 2,
# 2: 0, <--
# 3: 14,
# 4: 2,
# 5: 14,
# 6: 5,
# 7: 5,
# 8: 0, <--
# 9: 0, <--
# 10: 5,
# 11: 5,
# 12: 14,
# 13: 2,
# 14: 14,
# 15: 0, <--
# 16: 2}А это — нечётные степени двойки, взятые по модулю:
[pow(2, i, mod) for i in range(1, mod, 2)]
# [2, 8, 15, 9, 2, 8, 15, 9]В более общем случае это нечётные степени числа .
Нечётные степени не очень удобны для быстрого преобразования Фурье. Тут остаётся последний шаг — факторизовать матрицу Вандермонда для чисел , превратив в произведение матрицы Фурье и диагональной (которая не мешает, потому что на неё можно быстро умножать):
Итак, с перемножением многочленов по модулю разобрались — вернёмся к анализу сложности алгоритма. Поскольку мы перешли от многочленов порядка к многочленам порядка
, множитель 2 в формуле сложности алгоритма исчезает:
Глубина рекурсии остаётся порядка , но без накапливающегося множителя-двойки
также становится порядка
:
Суммарная сложность теперь имеет вид
Что наконец-то превосходит первый алгоритм Шенхаге-Штрассена!
Собираем алгоритм
Итак! Перейдём к полному описанию второго алгоритма.
Формулируем изначальную задачу как задачу умножения по модулю
. Какие бы у нас ни были изначально числа, всегда можно взять
достаточно большим, чтобы результат умножения влез в
бит. Для удобства рекурсии выбираем в качестве
степень двойки.
Выбираем числа
и
такие, что
и
. Есть хитрые формулы для наилучшего выбора, я их приводить не буду; можно подсмотреть в [5]. Делим входные числа, которые нужно перемножить, на
частей по
бит.
Превращаем в многочлены с коэффициентами, содержащими
бит, то есть добавляем несколько нулевых бит, чтобы промежуточные вычисления помещались без переполнения.
Теперь у нас на руках два вектора коэффициентов многочленов. Векторы длины
, числа в них длины
бит. Эти векторы умножаем сперва на диагональную матрицу (в формулах выше) за
, потом делаем быстрое преобразование Фурье за
.
Полученные векторы перемножаем поэлементно. Для перемножения чисел по модулю
используем рекурсивно этот же самый алгоритм (или простые алгоритмы, если числа уже достаточно маленькие). Здесь будет рекурсия глубины
.
К получившемуся вектору применяем обратное преобразование Фурье за
, потом умножаем на обратную диагональную матрицу за
.
(Обратите внимание на слишком длинный элемент 1000000 в этом примере — это ровно, наибольшее число, разрешённое модульной арифметикой!)
Из получившегося вектора коэффициентов многочлена-произведения восстанавливаем число-результат умножения, суммируя в столбик справа налево за
.
Вот и всё! Все гениальные приёмы второго алгоритма Шенхаге-Штрассена лежат у нас перед глазами. Конечно, для реализации этого алгоритма, эффективной на практике, нужно учесть ещё много нюансов и применить много приёмов; но на уровне идейном мы освоили его целиком.
В совсем не таком уж далёком 1960 году Андрей Колмогоров, один из величайших математиков своего времени, выдвинул гипотезу, что невозможно умножать числа быстрее, чем за . И совершенно изумительно видеть, насколько быстрее оказалось возможно умножать числа, чем это изначально предполагалось. В этой статье мы рассмотрели четыре основополагающих алгоритма, перейдя от
к
; для их понимания нам пришлось разобраться в теории Фурье, модульной арифметике и алгебре многочленов.
За рамками статьи остался алгоритм Фюрера и его варианты, а также опубликованный в 2020-м году [6] алгоритм с заявленной сложностью ; если эта статья окажется востребована, возможно, когда-нибудь мы разберём и их.
Спасибо за внимание!
P. S.
Эту статью я старался написать максимально популярно, избегая присущей учебникам математической строгости. Некоторые формулы намеренно упрощены, где-то вообще удалось обойти без них (мало где); в их оформлении там, где они остались, я сделал акцент на читаемость с ходу, без разбора с бумажкой и ручкой (выделение цветом, зачёркивание сокращённых величин); также я старался избегать математической терминологии, где это возможно («арифметика по модулю» вместо «в кольце вычетов по модулю»). Судьёй того, насколько моя задумка удалась, предстоит быть тебе, читатель; мне же остаётся лишь надеяться, что кто-то сможет почерпнуть из этого текста свежий взгляд на математику, обычно такую возвышенно-труднодоступную.
Литература
Pan, Victor. "How can we speed up matrix multiplication?." SIAM review 26.3 (1984): 393-415. PDF
Pan, Victor. "Strassen's algorithm is not optimal trilinear technique of aggregating, uniting and canceling for constructing fast algorithms for matrix operations." 19th Annual Symposium on Foundations of Computer Science (sfcs 1978). IEEE, 1978.
Pan, Victor. "How bad are Vandermonde matrices?." SIAM Journal on Matrix Analysis and Applications 37.2 (2016): 676-694. PDF
Pharr, Matt, and Randima Fernando. GPU Gems 2: Programming techniques for high-performance graphics and general-purpose computation (gpu gems). Addison-Wesley Professional, 2005. HTML
Kruppa, Alexander. "A GMP-based implementation of Schonhage-Strassen’s large integer multiplication algorithm." PDF
Harvey, David, and Joris Van Der Hoeven. "Integer multiplication in time O (n log n)." Annals of Mathematics 193.2 (2021): 563-617. PDF