Comments 37
Гоняя энтерпрайзные json-ы, я уже и забыл, какой красивой бывает математика. Спасибо, что напомнили *tears* *awe*
Вот примерно такого объяснения я ожидал от репетитора по математике. Она мне про производные, а я объясняю, что пока не пойму, ЧТО это, я не смогу сделать больше, чем зубрить формулы.
Блеск ! Хотелось бы надеяться на продолжение.
Часто используют кубические кривые, так как они могут иметь самые разные формы, и, соединив несколько их кусочков, можно получить практически что угодноТакое объяснение несколько расплывчато. На самом деле, сплайн удобен тем, что непрерывен сам, а также имеет непрерывные первую и вторую производные (вторая уже может быть с «зубчиками», т.е. третья производная непрерывной не будет). При этом строится он очень просто, построение сводится к решению системы линейных уравнений с трехдиагональной матрицей, такая система легко решается методом прогонки даже для очень большого числа коэффициентов, т.е. точек интерполяции
Годная популярная статья. Особенно понравилось:
Возможно читатель когда-то задавался вопросом: "Какую форму должна иметь дорога, чтобы по ней можно было ехать на квадратных колёсах без тряски?"
Невероятная эффективность математики в естественных науках есть нечто граничащее с мистикой, ибо никакого рационального объяснения этому факту нет.
Юджин Вигнер, нобелевский лауреат
Этому есть вполне рациональное объяснение. Математику придумал человек, а человек это часть природы, и мозг его развивался по тем же самым законам, что и объективная реальность.
Кто придумал все эти кривые первой, второй и следующих степеней?
Точнее - почему милые нам коники отписываются уравнениями первой и второй степени и в чём тут заслуга человека?
Они не придумали - они лишь описали, с помощью математического аппарата. Грубо говоря в том, что окружность - это точки равноудалённые от центра нет заслуги ни Эйлера ни кого-либо из известных на Земле математиков.
Угу, а сам математический аппарат придумал Бог и передал его в библии через откровения Иоанна.
Следуя вашей логики передал тогда уж через Архимеда, Ньютона, Гаусса, Эйлера и других.
Но согласитесь - называть математиков теми, кто придумал окружность, параболу и другие коники - смешно. В лучшем случае они их описали и систематизировали - предложили математический аппарат для коников. Но явно не объяснили, почему эти кривые связаны между собой таким образом.
Смешно называть математиками людей, которые эту самую математику и придумали? У вас очень странное чувство юмора. А если непонятно почему — обращайтесь к основам и первоисточникам, "нет царского пути в математике"(с).
Мы говорим совершенно про разные вещи - вы пытаетесь абсолютизировать математику, чуть ли не как творца всего сущего, а я вижу в математиках только лишь художников, описывающих, с помощью математического аппарата, то, что вокруг нас. Ниже в комментариях эта тема (математика как описание природы) уже обсуждается.
с помощью математического аппаратаМатематический аппарат не существует сам по себе в объективной реальности. Его придумали. Так же, как и придумали множество других интересных вещей, например буквы и кулинарию. Идея того, что математика абсолютна — это пережитки религиозных взглядов древних людей. Десятичная система счисления проистекает из количества пальцев на руках, это даже дети знают. Круг, как математическая абстракция, проистекает из наблюдения, что между солнцем, луной и шляпкой гриба есть что-то общее. Вот из попыток выделить это что-то общее и появилось процитированное вами определение. Если почитать другие, отличные от школьных учебников книги, можно найти очень много самых разных определений самых разных абстракций. Если вы не понимаете, почему в сечении конуса получается парабола — ну попробуйте для начала самостоятельно найти эту кривую через решение уравнения пересечения конуса с плоскостью.
Вы, похоже, просто не вчитываетесь в мои слова: я говорю про все коники, а не про конкретную параболу - про то, что внезапно оказалась общность у тех простых кривых первого - второго - третьего уровня, которые использует природа вокруг нас. То есть бац и конус - это то общее, что лежит в основе и круглого и параболического и гиперболического того, что использует природа.
Это совсем не бац, потому что логично, и не природа использует, а человек. В природе нет ни конусов, ни синусов, ни парабол. Природа живёт по своим законам, а математика эти законы идеализирует и упрощает. Вы можете взять срез от конуса с экспоненциальным расширением и внезапно обнаружить, что нету такой функции для описания получившейся кривой. Тогда, при желании, вы можете ввести свою, новую функцию, найти и обосновать способы её вычисления, свойства и связи с другими функциями. Вот так и развивается мат.аппарат.
собственно, математика началась как описание природы. Геометрия и астрономия именно об этом. А природа устроена на основании малого набора правил. Наблюдаемый мир — следствие этих правил. Через это математика (т.е. абстракция) из одной области работает в какой-то совсем другой. Потому что и первая и вторая функционирует на основании одного и того же малого набора правил.
Это верно. Математика началась(!) как описание природы. - но, во времена Лобачевского, все продолжали считать что "чистой математики" быть не может. Именно за это гнобили Лобачевского и именно поэтому Гаусс не решался публиковать свои некоторые работы.
Лобачевский также считал что иначе быть не может - он искал в природе подтверждение своей геометрии.
Как? - запирался в большом актовом зале университета и мерил углы. - да, он считал что его геометрия работает на больших расстояниях
Каких больших? - неизвестно. Он мог мерить углы в большом актовом зале университета. Вот и мерил там.
Вообще это уже философия- лет так 200 назад произошла революция и в математики и в других сферах жизни - люди осознали и за это их не стали гнобить, что может быть просто "чистая математика" и можно, в живописи, рисовать просто букет цветов, а не букет как символ чего-то.
Кратко это выразил (обобщил) Фрейд - "Иногда сигара это просто сигара." (С)
Пожалуйста, продолжайте.
А если расширить взгляд на коники, то там будут и кривые первого порядка (две пересекающиеся и одна прямая) и "кривая нулевого порядка" — точка. Так?
Утверждение «геометрического определения прямой просто не существует» тоже не совсем верное, поскольку просто нет смысла выражать объекты через самих себя. Прямую можно выразить, например, через отрезок бесконечной длины, а отрезок — как минимальный путь между двумя точками. В реальном мире геометрия тоже реальна и существует вместе с физикой, а не по отдельности. Ещё можно сказать, что прямая — это линия, прочерченная с помощью линейки. И это не так уж и глупо, как может показаться на первый взгляд, поскольку геометрия развивалась именно для решения задач циркулем и линейкой.
Категорически не хватает описания такой трёхмерной фигуры, как "гиперболический параболоид". На лекциях по высшей математике им забавно голову взрывают.
Категорически не хватает описания такой трёхмерной фигуры, как «гиперболический параболоид». На лекциях по высшей математике им забавно голову взрывают.
Он выглядит так:

Только это поверхность, а автор пока в своем повествовании не дошел еще даже до трехмерных кривых, думаю, что дойдет. Ну, и именно гиперболического параболоида для взрывания мозга недостаточно, название сложное, а поверхность относительно простая
Для взрывания головы можно начать с выворачивания поверхности наизнанку)
Ну, насколько помню, через неё в любой точке можно провести прямую, которая будет целиком находиться на этой поверхности. Это достаточно сильно озадачивало...
Эта кривая имеет большое значение в зубчатом зацеплении, ведь если выточить зубья на шестернях по эвольвенте окружности и правильно соблюсти расстояние между соседними зубьями, то получится зубчатая передача, работающая без стука. Это означает, что контакт между шестернями всегда сохраняется, и поэтому обе шестерни могут двигаться равномерно.
Смысл не только в стуке. Проблема стука решается не эвольвентой как таковой, а тем, что в зацеплении одновременно находится одновременно 2-3 зуба. Одно из важнейших свойств эвольвенты - зубья движутся относительно друг друга без проскальзывания (катятся друг по другу), что минимизирует износ и потери на трение. Причём это свойство сохраняется при любом числе зубьев на шестернях (при сохранении профиля зуба), что позволяет делать коробки перемены передач (одна шестерня может поочередно контактировать с несколькими разными). Кроме того, эвольвентное зацепление не очень требовательно к межцентровому расстоянию, а форма зуба на ведущей и ведомой шестерне одинакова, т.е. для нарезки можно использовать один и тот же инструмент (в отличие от альтернативного зацепления Новикова).
В упомянутых в начале статьи часах, кстати, зачастую используется не эвольвентное, а циклоидальное зацепление. Связано это с тем, что шестерня с эвольвентными зубьями при числе зубьев менее 17 требует подрезки зуба - поднутрения в его основании, иначе зацепление не будет работать. Чем меньше зубьев - тем больше подрезка, а у часовых шестеренок в силу специфики (малые габариты и большое передаточное отношение) бывает и 6 зубьев - с эвольвентой основание получится слишком тонким.
В часовых механизмах изпользуется не эвольвентное, а циклоидное зацепление: https://en.wikipedia.org/wiki/Cycloid_gear
Хотелось бы видеть подобные статьи с этой вашей геометрией побольше, очень интересно :)
Насколько я помню, в часовых механизмах обычно используют не эвольвентное, а циклоидное зацепление...


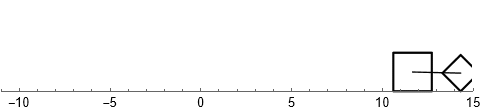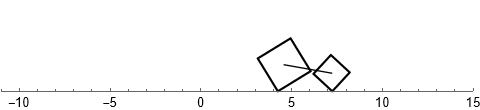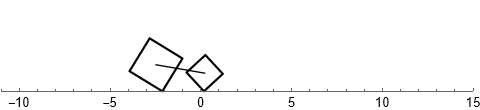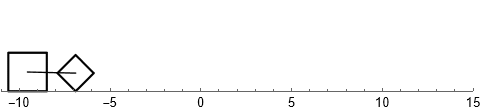


Какая ты кривая, или математика вокруг нас