Monotirg Sep 14 2023 at 17:37

Циркуль и линейка. Часть 1

Easy

22 min

11K

Всем привет!

Как-то раз мне захотелось сделать анимацию построения фигуры циркулем и линейкой. Немного погуглив, обнаружил, что на английском compass это ещё и циркуль, и что подходящего готового решения нет.

Всё дальнейшее вылилось в эту статью.

Короткое предисловие

Статью я разделил на две части. В первой — реализация циркуля и линейки, а во второй уже создание анимации на основе написанных классов.

Сразу проясню некоторые моменты. Писать я буду на python, потому что нужная мне библиотека для анимации (ссылка на неё в конце) написана на нём. Ещё я не стал идти по стандартному шаблону, когда для точек создаётся структура. Опять таки из‑за библиотеки для анимации, в которой точки хранятся в массиве numpy.

Таким образом, пока что мне понадобится только python и numpy.

Циркуль

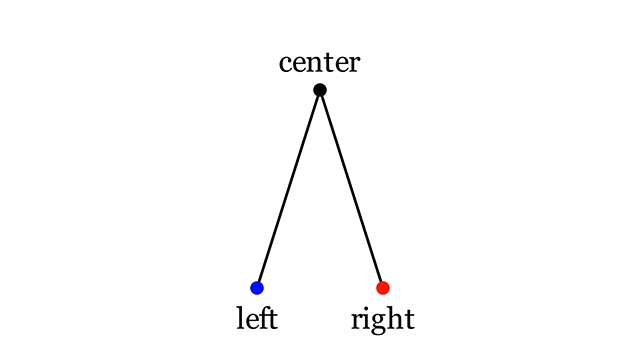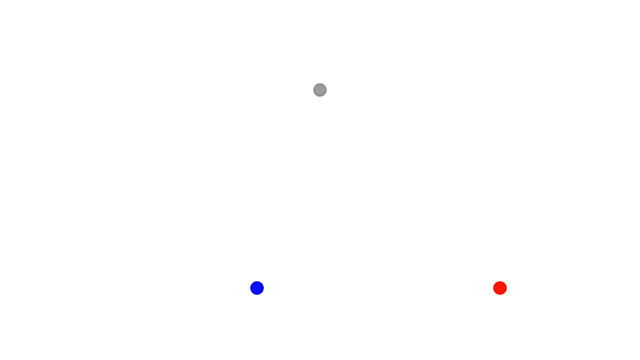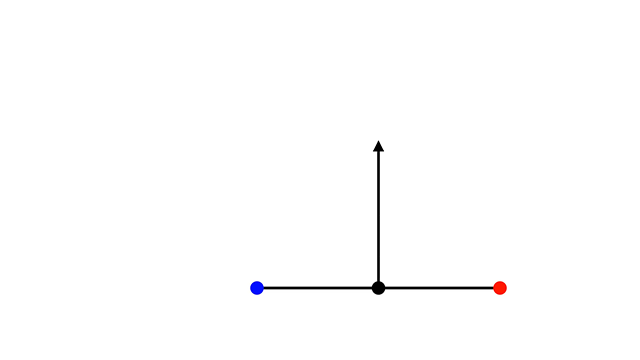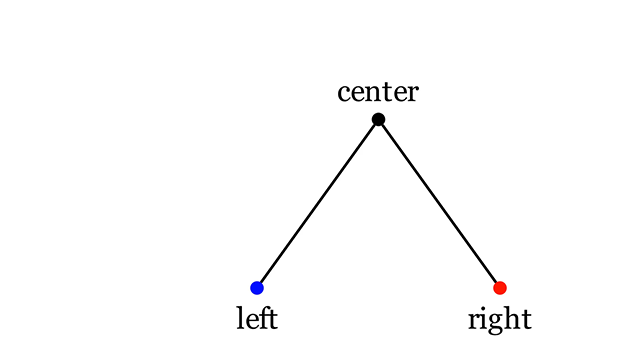
Под циркулем мы будем понимать три точки: left , right и center. Определить циркуль можно и по-другому, но этот способ мне кажется наиболее простым и понятным.

Точки left и right должны быть равноудалены от точки center и все три точки не должны лежать на одной прямой. Чтобы проверить это условие, достаточно вычислить длины отрезков left, center и right, center, а также псевдоскалярное произведение векторов, построенных по точкам left, right и left, center.

Коротко напомню, псевдоскалярное произведение вычисляется так

$a \vee b = \begin{vmatrix} a_1 & a_2 \\ b_1 & b_2\end{vmatrix} = a_1b_2-a_2b_2,$

и оно равняется нулю тогда и только тогда, когда векторы коллинеарны. Кроме того, по знаку можно судить о взаимном расположении векторов.

Если положительный угол между векторами a и b меньше 180 градусов, то псевдоскалярное произведение, положительное, если больше, то отрицательное

По итогу, конструктор класса выглядит так.

class Compass:
    def __init__(
        self,
        left: np.ndarray,
        right: np.ndarray,
        center: np.ndarray
    ):
        det = np.linalg.det(np.vstack((center - left, center - right)))
        
        if np.isclose(det, 0):
            raise ValueError("collinear points")
        if np.isclose(
                np.linalg.norm(center - left), np.linalg.norm(center - right)
            ):
                raise ValueError("invalid center")
        
        self.left = left
        self.right = right
        self.center = center

Определим ещё свойства:

radius — радиус окружности, который можно построить с помощью циркуля.
length — длина ножки циркуля.
outer_center — определяет, где находится center относительно прямой, проходящей через точки left и right. Если center находится слева от прямой в направлении от left к right, то outer_center = True, иначе outer_center = False. Проверяется это также с помощью псевдоскалярного произведения.

@property
def outer_center(self):
    det = np.linalg.det(np.vstack((self.right - self.left, self.center - self.left)))
    return True if det > 0 else False

@property
def length(self):
    return np.linalg.norm(self.center - self.left)

@property
def radius(self):
    return np.linalg.norm(self.right - self.left)

Вспомогательные методы

Прежде чем переходить к методам, отвечающим за манипуляции с циркулем, определим вспомогательные методы.

Первый — вычисление нормального вектора к прямой, проходящей через точки left и right. Для этого возьмём вектор, построенный по точкам left, right. Нормируем его и поменяем координаты местами, умножив при этом одну из них на минус единицу.

Почему это работает

Во-первых, если у единичного вектора поменять местами координаты и умножить одну из координат на минус единицу, то полученный вектор будет единичным, что проверяется просто по формуле длины вектора.

Во-вторых, полученный вектор будет перпендикулярен к изначальному, так как скалярное произведение равно нулю, что проверяется вычислением скалярного произведения.

Есть ещё и совсем короткое объяснение, для которого нужно воспользоваться комплексными числами и их геометрическим представлением. По сути, мы сопоставляем вектору комплексное число и умножаем его на мнимую единицу, тем самым поворачиваем его на 90 градусов.

Добавим параметр outer, отвечающий за выбор направления нормального вектора. Если outer = True, то вектор нормали направлен влево относительно прямой, проходящей через точки left и right, в противном случае вправо.

def _normal_vec(self, outer: bool):
    vec = (self.right - self.left) / self.radius
    normal_vec = np.array([-vec[1], vec[0]])
    det = np.linalg.det(np.vstack((vec, normal_vec)))
    
    if outer:
        return np.sign(det) * normal_vec
    
    return -np.sign(det) * normal_vec

Второй — вычисление угла между векторами. Важно, что здесь нужен не наименьший угол между векторами, а направленный. То есть такой угол, на которой нужно повернуть в положительном направлении (против часовой стрелки) первый вектор, чтобы он совпал со вторым.

Для этого используется функция arctan2, которая возвращает угол между осьюи вектором в пределах от $-180^\circ$ до $180^\circ$ .

Чтобы найти искомый угол, нужно вычислить для двух векторов углы с осью и взять их разность. Здесь важно учитывать, какой угол из какого вычитается. Поэтому будем считать, что поворачивается вектор vec1 к вектору vec2, то есть из второго угла вычитается первый.

def _angle_vec(self, vec1: np.ndarray, vec2: np.ndarray):
    return np.arctan2(vec2[1], vec2[0]) - np.arctan2(vec1[1], vec1[0])

Определение центра

Часто неудобно и не нужно точно определять, где находится точка center. Поэтому добавим метод для её вычисления по точкам left и right. Он будет принимать параметр height, который отвечает за расстояние точки center до прямой, проходящей через точки left и right, и параметр outer, который отвечает за то, где находится center относительно этой прямой.

Воспользуемся тем, что на трех точках циркуля можно построить равнобедренный треугольник, а в равнобедренном треугольнике высота, проведенная к основанию, является и медианой. Поэтому нужно найти середину отрезка left, right и отложить от неё вектор нормали, умноженный на height. Конец вектора будет точкой center.

def init_center(self, height: float, outer: bool):
    self.center = 0.5 * (self.right + self.left) + height * self._normal_vec(outer)

Теперь можно немного изменить конструктор класса.

class Compass:
    def __init__(
        self,
        left: np.ndarray,
        right: np.ndarray,
        center: np.ndarray = None,
        outer_center: bool = True,
    ):
        self.left = left
        self.right = right
        self.center = center

        if center is None:
            self.init_center(self.radius, outer_center)
        else:
            det = np.linalg.det(np.vstack((center - left, center - right)))
             if np.isclose(
                np.linalg.norm(center - left), np.linalg.norm(center - right)
            ):
                raise ValueError("invalid center")
            if np.isclose(det, 0):
                raise ValueError("collinear points")

Переворот

Для переворота циркуля нужно отразить точку center относительно прямой, проходящей через точки left и right. Сделать это можно исходя из геометрических соображений. Представим, что циркуль уже перевёрнут. Тогда на трех точках left, right, center и точке new_center, полученной после переворота, можно построить ромб. Это даёт следующее.

Во-первых, противоположные стороны равны и параллельны, то есть вектор, построенный по точкам left и new_center, равен вектору, построенному по точкам center и right.

Во-вторых, диагонали ромба перпендикулярны и делятся пополам в точке пересечения, то есть точка new_center симметрична точке center относительно прямой, проходящей через точки left и right.

Поэтому, чтобы найти new_center, нужно отложить вектор center, right от точки left, и конец вектора будет точкой new_center.

def flip(self):
    self.center = self.right + self.left - self.center

Повороты

Сначала опишем поворот циркуля относительно произвольной точки point.

Поворот циркуля относительно точки center

Делается это следующим образом. Нужно сдвинуть все точки циркуля на -point, повернуть получившиеся точки относительно начала координат, то есть умножить слева на матрицу поворота

$M =\begin{pmatrix} \cos{\alpha} & -\sin{\alpha} \\ \sin{\alpha} & \cos{\alpha} \end{pmatrix},$

и сдвинуть их обратно. Если записать все преобразования в виде формулы, то получим

$\begin{pmatrix}x' \\ y' \end{pmatrix} = \begin{pmatrix} \cos{\alpha} & -\sin{\alpha} \\ \sin{\alpha} & \cos{\alpha} \end{pmatrix} \left( \begin{pmatrix}x\\ y \end{pmatrix} - \begin{pmatrix}p_x \\ p_y \end{pmatrix}\right) + \begin{pmatrix}p_x \\ p_y \end{pmatrix}.$

def rotate_about_point(self, angle: float, point: np.ndarray):
    rot_mat = np.array([
        [np.cos(angle), -np.sin(angle)], 
        [np.sin(angle), np.cos(angle)]
    ])
    self.left = np.matmul(rot_mat, self.left - point) + point
    self.right = np.matmul(rot_mat, self.right - point) + point
    self.center = np.matmul(rot_mat, self.center - point) + point

Теперь можно описать повороты, которые чаще всего используются.

 def rotate_about_center(self, angle: float):
    self.rotate_about_point(angle, self.center)

def rotate_about_left(self, angle: float):
    self.rotate_about_point(angle, self.left)

def rotate_about_right(self, angle: float):
    self.rotate_about_point(angle, self.right)

Но есть и ещё один тип поворотов, когда нужно повернуть одну из ножек циркуля так, чтобы она попала в точку point.

Пример из первой анимации, где это используется

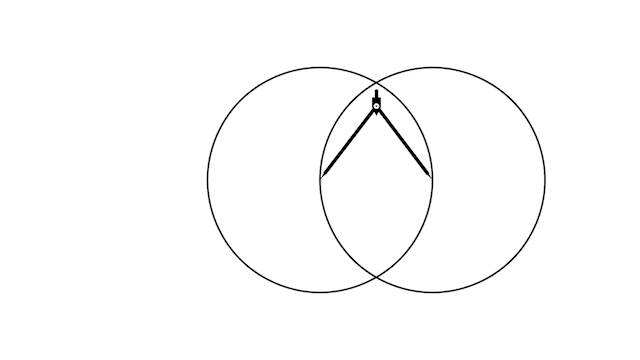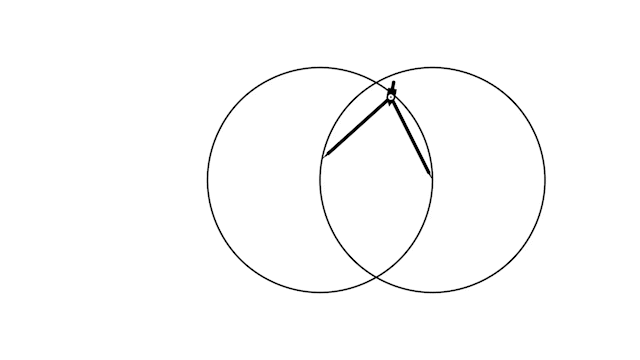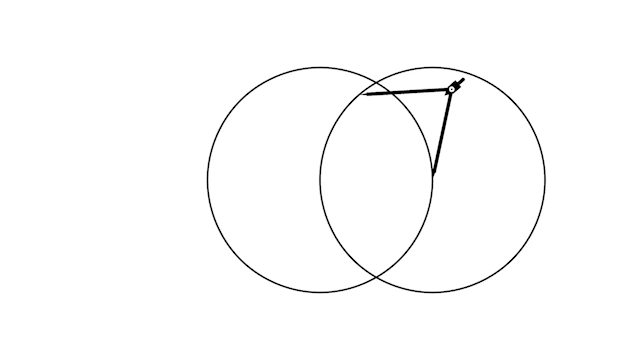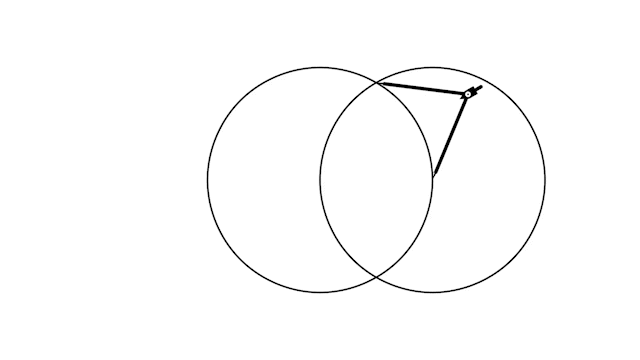
Важно, что это не всегда возможно, поэтому после поворота нужно проверить, что ножка циркуля действительно попала в точку point.

def rotate_left_to(self, point: np.ndarray):
    angle = self._angle_vec(self.left - self.right, point - self.right)
    self.rotate_about_right(angle)

    if not np.allclose(self.left, point):
        raise ValueError("can't rotate to chosen point")

def rotate_right_to(self, point: np.ndarray):
    angle = self._angle_vec(self.right - self.left, point - self.left)
    self.rotate_about_left(angle)

    if not np.allclose(self.right, point):
        raise ValueError("can't rotate to chosen point")

Изменение радиуса

Изменить радиус циркуля можно двумя способами. Первый, когда одна из ножек циркуля фиксируется, а другая сдвигается до нужного радиуса. Второй, когда две ножки сдвигаются одновременно. Начнем с первого способа.

Во-первых, нужно определить на сколько и в каком направлении сдвигается одна из точек. Для определённости будем считать, что сдвигается точка right. Тогда она сдвигается к точке left, если изначальный радиус больше нового. В противном случае она сдвигается от точки left. В обоих случаях точка right сдвигается на модуль разницы радиусов. Записать это можно так

self.right += (new_radius / self.radius - 1) * (self.right - self.left)

Во-вторых, нужно определить, где будет находиться точка center после сдвига. Для этого достаточно знать, на каком расстоянии от прямой, проходящей через точки left и right, она должна быть. Так как при сдвиге длина ножек не изменяется, опять воспользуемся тем, что на трех точках циркуля можно построить равнобедренный треугольник, и высота к основанию в нем является медианой. Тогда по теореме Пифагора высота вычисляется так

height = (self.length**2 - 0.25 * new_radius**2) ** 0.5

Теперь можно вычислить координаты точки center с помощью метода init_center.

Остаётся лишь проверить, что возможно сдвинуть ножку циркуля так, чтобы получить новый радиус. Предельный случай получается, когда center лежит на середине отрезка left, right, то есть новый радиус должен быть меньше удвоенной длины ножки циркуля.

def change_radius_to_right(self, new_radius: float):
    if new_radius >= 2 * self.length or new_radius <= 0:
        raise ValueError("invalid radius")

    height = (self.length**2 - 0.25 * new_radius**2) ** 0.5
    self.right += (new_radius / self.radius - 1) * (self.right - self.left)
    self.init_center(height, self.outer_center)

def change_radius_to_left(self, new_radius: float):
    if new_radius >= 2 * self.length or new_radius <= 0:
        raise ValueError("invalid radius")

    height = (self.length**2 - 0.25 * new_radius**2) ** 0.5
    self.left += (new_radius / self.radius - 1) * (self.left - self.right)
    self.init_center(height, self.outer_center)

Когда одновременно сдвигаются две ножки циркуля, то нужно сделать всё тоже самое, но сдвиги будут не на модуль разности радиусов, а на половину того же модуля.

def change_radius(self, new_radius: float):
    if new_radius >= 2 * self.length or new_radius <= 0:
        raise ValueError("invalid radius")
    
    height = (self.length**2 - 0.25 * new_radius**2) ** 0.5
    radius = self.radius
    vec = self.right - self.left
    self.left -= 0.5 * (new_radius / radius - 1) * vec
    self.right += 0.5 * (new_radius / radius - 1) * vec
    self.init_center(height, self.outer_center)

Изменение угла

Изменить угол циркуля можно с помощью изменения радиуса и сдвига циркуля. Но я решил пойти обычным путём.

Поэтому для начала вычислим угол между ножками циркуля. Замечу, что он обязательно будет от $0^\circ$ до $180^\circ$ . В очередной раз воспользуемся тем, что на точках циркуля можно построить равнобедренный треугольник, и высота к основанию в нём является биссектрисой. Поэтому, чтобы получить нужный угол, нужно повернуть каждую из ножек относительно точки center на следующий угол:

$\gamma = \frac{1}{2}(\theta - \alpha).$

Здесь $\theta$ - угол между ножками циркуля, а $\alpha$ - угол, который хотим получить. Для выполнения поворота теперь нужны две матрицы поворота, которые поворачивают на одинаковый угол, но в противоположных направлениях. Кроме того, чтобы выбрать правильное направление поворота для каждой ножки, нужно учитывать положение точки center относительно прямой, проходящей через точки left и right.

И не забываем про то, что нельзя вывернуть или полностью сложить циркуль, поэтому новый угол должен быть от $0^\circ$ до $180^\circ.$

def change_angle(self, angle: float):
    if angle >= np.pi or angle <= 0:
        raise ValueError("invalid angle")
    
    vec_left = self.left - self.center
    vec_right = self.right - self.center
    current_angle = self._angle_vec(vec_left, vec_right)
    new_angle = 0.5 * (current_angle - angle)
    rot_mat = np.array([
        [np.cos(new_angle), -np.sin(new_angle)],
        [np.sin(new_angle), np.cos(new_angle)],
    ])
    
    if self.outer_center:
        self.left = np.matmul(rot_mat, vec_left) + self.center
        self.right = np.matmul(rot_mat.transpose(), vec_right) + self.center
    else:
        self.left = np.matmul(rot_mat.transpose(), vec_left) + self.center
        self.right = np.matmul(rot_mat, vec_right) + self.center

Сдвиг и перемещение

Для сдвига циркуля нужно сдвинуть каждую точку циркуля на один и тот же вектор vec.

def shift(self, vec: np.ndarray):
    self.left += vec
    self.right += vec
    self.center += vec

Но чаще всего циркуль нужно сдвинуть так, чтобы одна из его точек попала в определенную точку point, что легко сделать с помощью обычного сдвига.

def move_to(self, point: np.ndarray):
    self.shift(point - (self.left + self.right + self.center) / 3)

def move_left_to(self, point: np.ndarray):
    self.shift(point - self.left)

def move_right_to(self, point: np.ndarray):
    self.shift(point - self.right)

def move_center_to(self, point: np.ndarray):
    self.shift(point - self.center)

Полный код циркуля

import numpy as np


class Compass:
    def __init__(
        self,
        left: np.ndarray,
        right: np.ndarray,
        center: np.ndarray = None,
        outer_center: bool = True,
    ):
        self.left = left
        self.right = right
        self.center = center

        if center is None:
            self.init_center(self.radius, outer_center)
        else:
            det = np.linalg.det(np.vstack((center - left, center - right)))

            if np.isclose(
                np.linalg.norm(center - left), np.linalg.norm(center - right)
            ):
                raise ValueError("invalid center")
            if np.isclose(det, 0):
                raise ValueError("collinear points")

    @property
    def outer_center(self):
        det = np.linalg.det(
            np.vstack((self.right - self.left, self.center - self.left))
        )
        return True if det > 0 else False

    @property
    def length(self):
        return np.linalg.norm(self.center - self.left)

    @property
    def radius(self):
        return np.linalg.norm(self.right - self.left)

    def _normal_vec(self, outer: bool):
        vec = (self.right - self.left) / self.radius
        normal_vec = np.array([-vec[1], vec[0]])
        det = np.linalg.det(np.vstack((vec, normal_vec)))

        if outer:
            return np.sign(det) * normal_vec

        return -np.sign(det) * normal_vec

    def _angle_vec(self, vec1, vec2):
        return np.arctan2(vec2[1], vec2[0]) - np.arctan2(vec1[1], vec1[0])

    def init_center(self, height: float, outer: bool):
        self.center = 0.5 * (self.right + self.left) + height * self._normal_vec(outer)

    def flip(self):
        self.center = self.right + self.left - self.center

    def rotate_about_point(self, angle: float, point: np.ndarray):
        rot_mat = np.array([
            [np.cos(angle), -np.sin(angle)], 
            [np.sin(angle), np.cos(angle)]
        ])
        self.left = np.matmul(rot_mat, self.left - point) + point
        self.right = np.matmul(rot_mat, self.right - point) + point
        self.center = np.matmul(rot_mat, self.center - point) + point

    def rotate_about_center(self, angle: float):
        self.rotate_about_point(angle, self.center)

    def rotate_about_left(self, angle: float):
        self.rotate_about_point(angle, self.left)

    def rotate_about_right(self, angle: float):
        self.rotate_about_point(angle, self.right)

    def rotate_left_to(self, point: np.ndarray):
        angle = self._angle_vec(self.left - self.right, point - self.right)
        self.rotate_about_right(angle)

        if not np.allclose(self.left, point):
            raise ValueError("can't rotate to chosen point")

    def rotate_right_to(self, point: np.ndarray):
        angle = self._angle_vec(self.right - self.left, point - self.left)
        self.rotate_about_left(angle)

        if not np.allclose(self.right, point):
            raise ValueError("can't rotate to chosen point")

    def change_angle(self, angle: float):
        if angle >= np.pi or angle <= 0:
            raise ValueError("invalid angle")

        vec_left = self.left - self.center
        vec_right = self.right - self.center
        current_angle = self._angle_vec(vec_left, vec_right)
        new_angle = 0.5 * (current_angle - angle)
        rot_mat = np.array([
            [np.cos(new_angle), -np.sin(new_angle)],
            [np.sin(new_angle), np.cos(new_angle)],
        ])

        if self.outer_center:
            self.left = np.matmul(rot_mat, vec_left) + self.center
            self.right = np.matmul(rot_mat.transpose(), vec_right) + self.center
        else:
            self.left = np.matmul(rot_mat.transpose(), vec_left) + self.center
            self.right = np.matmul(rot_mat, vec_right) + self.center

    def change_radius_to_right(self, new_radius: float):
        if new_radius >= 2 * self.length or new_radius <= 0:
            raise ValueError("invalid radius")

        height = (self.length**2 - 0.25 * new_radius**2) ** 0.5
        self.right += (new_radius / self.radius - 1) * (self.right - self.left)
        self.init_center(height, self.outer_center)

    def change_radius_to_left(self, new_radius: float):
        if new_radius >= 2 * self.length or new_radius <= 0:
            raise ValueError("invalid radius")

        height = (self.length**2 - 0.25 * new_radius**2) ** 0.5
        self.left += (new_radius / self.radius - 1) * (self.left - self.right)
        self.init_center(height, self.outer_center)

    def change_radius(self, new_radius: float):
        if new_radius >= 2 * self.length or new_radius <= 0:
            raise ValueError("invalid radius")

        height = (self.length**2 - 0.25 * new_radius**2) ** 0.5
        radius = self.radius
        vec = self.right - self.left
        self.left -= 0.5 * (new_radius / radius - 1) * vec
        self.right += 0.5 * (new_radius / radius - 1) * vec
        self.init_center(height, self.outer_center)

    def shift(self, vec: np.ndarray):
        self.left += vec
        self.right += vec
        self.center += vec

    def move_to(self, point: np.ndarray):
        self.shift(point - (self.left + self.right + self.center) / 3)

    def move_left_to(self, point: np.ndarray):
        self.shift(point - self.left)

    def move_right_to(self, point: np.ndarray):
        self.shift(point - self.right)

    def move_center_to(self, point: np.ndarray):
        self.shift(point - self.center)

Линейка

С линейкой почти всё тоже самое, что и с циркулем. Чтобы её определить, нужно задать длину, ширину и количество больших и маленьких делений. Но в отличие от циркуля, придётся хранить гораздо больше точек.

Все эти точки можно разделить на три группы: shape, division и subdivision.

shape — точки, которые задают прямоугольник, то есть саму линейку.
division и subdivision — точки, которые задают большие и маленькие деления. Но нужно хранить не только точки начала делений, но и точки конца делений, то есть, по сути, отрезки. Я их буду хранить подряд, то есть в следующем порядке: начало первого деления, конец первого деления, начало второго деления, конец второго деления и так далее до последнего деления.

Пример линейки с двумя большими и четырьмя маленькими делениями

Теперь можно перейти к конструктору класса. На вход он получает параметры:

width, height — ширина и длина линейки.
division, subdivision — количество больших и маленьких делений.
padding_width — относительный отступ делений по ширине.
height_division, height_subdivision — относительная высота делений.

Изначально будем предполагать, что линейка расположена так, что её верхняя левая точка находится в начале координат. В этом случае определить точки shape совсем просто.

self.shape = np.array([[0, 0], [0, -height], [width, -height], [width, 0]])

Перейдём от относительных величин к абсолютным и изменим ширину с учётом отступа.

padding_width *= width
width -= padding_width
height_division *= height
height_subdivision *= height

Далее нужно определить точки division и subdivision, начнём с первых.

Чтобы получить координаты по, равномерно распределим точки на отрезке от 0 до width и сдвинем их вправо на половину отступа по ширине. Поскольку нужно хранить как начало деления, так и конец деления, то каждую координату нужно продублировать.

Для координат понужно продублировать 0, -height_division столько раз, сколько больших делений, так как начало деления лежит на самой линейки (координата поравна нулю), а координата поконца деления равна длине деления со знаком минус.

Осталось объединить координаты и транспонировать полученный массив, транспонирование делается исключительно для удобства.

div_x = np.linspace(0, width, division)
div_x += 0.5 * padding_width
div_x = np.repeat(div_x, 2)
div_y = np.full((division, 2), [0, -height_division])
self.division = np.vstack((div_x, div_y.reshape(-1))).transpose()

Для точек subdivision делаем тоже самое, только для координат пораспределяем точки между большими делениями.

subdiv_x = np.array([
    np.linspace(div_x[2 * i], div_x[2 * i + 2], subdivision + 2)[1:-1]
    for i in range(division - 1)
])
subdiv_x = np.repeat(subdiv_x.reshape(-1), 2)
subdiv_y = np.full(
    ((division - 1) * subdivision, 2), [0, -height_subdivision]
)
self.subdivision = np.vstack((subdiv_x, subdiv_y.reshape(-1))).transpose()

В конце для удобства добавим перемещение линейки в начало координат. Кроме того, нужно проверить, что количество больших делений больше двух.

По итогу, конструктор класса выглядит следующим образом.

import numpy as np


class Ruler:
    def __init__(
        self,
        width: float,
        height: float,
        division: int,
        subdivision: int = 0,
        padding_width: float = 0.1,
        height_division: float = 0.45,
        height_subdivision: float = 0.25,
    ):
        if division < 2:
            raise ValueError("invalid division")

        self.shape = np.array([[0, 0], [0, -height], [width, -height], [width, 0]])
        padding_width *= width
        width -= padding_width
        height_division *= height
        height_subdivision *= height

        div_x = np.linspace(0, width, division)
        div_x += 0.5 * padding_width
        div_x = np.repeat(div_x, 2)
        div_y = np.full((division, 2), [0, -height_division])
        self.division = np.vstack((div_x, div_y.reshape(-1))).transpose()

        self.subdivision = None
        if subdivision > 0:
            subdiv_x = np.array([
                np.linspace(div_x[2 * i], div_x[2 * i + 2], subdivision + 2)[1:-1]
                for i in range(division - 1)
            ])
            subdiv_x = np.repeat(subdiv_x.reshape(-1), 2)
            subdiv_y = np.full(
                ((division - 1) * subdivision, 2), [0, -height_subdivision]
            )
            self.subdivision = np.vstack((subdiv_x, subdiv_y.reshape(-1))).transpose()

        self.move_to(np.array([0, 0]))

Определим свойства start и end, которые возвращают начало первого и последнего большого деления.

@property
def start(self):
    return self.division[0]

@property
def end(self):
    return self.division[-2]

Дальнейшие методы повторяют методы циркуля, поэтому я не буду их так подробно расписывать, а больше остановлюсь на том, что изменилось.

Вспомогательные методы

Первый — всё тот же угол между векторами.

def _angle_vec(self, vec1: np.ndarray, vec2: np.ndarray):
    return np.arctan2(vec2[1], vec2[0]) - np.arctan2(vec1[1], vec1[0])

Второй — получение точки начала деления. На вход он получает индексы большого и маленького деления. Здесь важно учитывать то, что точки хранятся подряд (начало деления, конец деления и т.д.), поэтому индексы нужно умножать на два.

def _get_division(self, div: int, subdiv: int = None):
    div, subdiv = 2 * div, 2 * subdiv if subdiv is not None else None
    if div >= len(self.division):
        raise IndexError("division index out of range")
    if subdiv is None:
        return self.division[div]
    if self.subdivision is None:
        raise ValueError("subdivision is not defined")

    count_subdiv = len(self.subdivision) // (len(self.division) - 2)

    if subdiv >= 2 * count_subdiv:
        raise IndexError("subdivision index out of range")

    return self.subdivision[count_subdiv * div + subdiv]

Повороты

Как и с циркулем, опишем сначала поворот линейки относительно произвольной точки point.

def rotate_about_point(self, angle: float, point: np.ndarray):
    rot_mat = np.array([
        [np.cos(angle), np.sin(angle)], 
        [-np.sin(angle), np.cos(angle)]
    ])
    self.shape = np.matmul(self.shape - point, rot_mat) + point
    self.division = np.matmul(self.division - point, rot_mat) + point
    if self.subdivision is not None:
        self.subdivision = np.matmul(self.subdivision - point, rot_mat) + point

В отличие от циркуля, нужно повернуть каждую точку из массива точек. Для этого используем всю ту же функцию numpy.matmul, но теперь умножаем на матрицу поворота не слева, а справа. Всё потому, что массив точек имеет размер (k, 2), где k - количество точек, и его не получится матрично умножить слева на матрицу размера (2, 2).

Кроме того, если раньше использовалась такая матрица поворота

$M =\begin{pmatrix} \cos{\alpha} & -\sin{\alpha} \\ \sin{\alpha} & \cos{\alpha} \end{pmatrix},$

то теперь нужно брать транспонированную

$M^t = \begin{pmatrix} \cos{\alpha} & \sin{\alpha} \\ -\sin{\alpha} & \cos{\alpha} \end{pmatrix}.$

Почему это так

При повороте точек циркуля они умножались на матрицу поворота слева, другими словами, точки воспринимались как вектор-столбец. Теперь же умножение справа, то есть точки воспринимаются как вектор-строка.

Пусть- точка, воспринимаемая как вектор-строка, $\widetilde{x}$ - эта же точка после поворота.

Тогда при умножении слева точкии $\widetilde{x}$ связаны следующим равенством

$\widetilde{x}^t = M x^t.$

Воспользуемся свойствами транспонирования и получим

$\widetilde{x} = (\widetilde{x}^t)^t= (Mx^t)^t= xM^t.$

Остальные повороты выглядят так

def rotate_about_start(self, angle: float):
    self.rotate_about_point(angle, self.start)

def rotate_about_end(self, angle: float):
    self.rotate_about_point(angle, self.end)

def rotate_about_division(self, angle: float, division: int, subdivision: int = None):
    self.rotate_about_point(angle, self._get_division(division, subdivision))

def rotate_start_to(self, point: np.ndarray):
    angle = self._angle_vec(self.start - self.end, point - self.end)
    self.rotate_about_end(angle)
    product = np.dot(self.start - point, self.end - point)

    if not np.isclose(product, 0) and product > 0:
        raise ValueError("can't rotate to chosen point")

def rotate_end_to(self, point: np.ndarray):
    angle = self._angle_vec(self.end - self.start, point - self.start)
    self.rotate_about_start(angle)
    product = np.dot(self.start - point, self.end - point)

    if not np.isclose(product, 0) and product > 0:
        raise ValueError("can't rotate to chosen point")

Если для циркуля нужно было проверить, что одна из ножек циркуля попала в нужную точку, то для линейки условие немного другое. Нужно проверить, что точка лежит на линейки, то есть на отрезке. Для этого достаточно вычислить скалярное произведение векторов point, self.start и point, self.end и проверить, что оно меньше или равно нулю.

Почему это так

Для евклидовых пространств скалярное произведение можно записать в следующем виде

$(a,b)=|a||b|\cos{\alpha},$

где $\alpha$ - угол между векторамии, - длины векторови .

Пусть - первый и второй вектор, для которых вычисляется скалярное произведение выше. Важно заметить, что эти векторы коллинеарны, так как линейка уже повернута к точке.

Тогда, если точка лежит на отрезке, то угол между вектора равен $180^\circ$ , то есть скалярное произведение отрицательное, так как

$\cos{180^\circ}=-1.$

Если же точка лежит на конце отрезка, то скалярное произведение равно нулю, так как один вектор нулевой.

Наконец, если точка лежит не на отрезке, то угол между векторами равен $0^\circ$ , то есть скалярное произведение положительное, так как

$\cos{0^\circ} = 1.$

Сдвиг и перемещения

Сдвиг и перемещения полностью повторяют сдвиг и перемещения циркуля.

def shift(self, vec: np.ndarray):
    self.shape += vec
    self.division += vec

    if self.subdivision is not None:
        self.subdivision += vec

def move_to(self, point: np.ndarray):
    vec = 0.25 * np.sum(self.shape, axis=0)
    self.shift(point - vec)

def move_start_to(self, point: np.ndarray):
    self.shift(point - self.start)

def move_end_to(self, point: np.ndarray):
    self.shift(point - self.end)

def move_division_to(self, point: np.ndarray, division: int, subdivision: int = None):
    self.shift(point - self._get_division(division, subdivision))

Полный код линейки

import numpy as np


class Ruler:
    def __init__(
        self,
        width: float,
        height: float,
        division: int,
        subdivision: int = 0,
        padding_width: float = 0.1,
        height_division: float = 0.45,
        height_subdivision: float = 0.25,
    ):
        if division < 2:
            raise ValueError("invalid division")

        self.shape = np.array([[0, 0], [0, -height], [width, -height], [width, 0]])
        padding_width *= width
        width -= padding_width
        height_division *= height
        height_subdivision *= height

        div_x = np.linspace(0, width, division)
        div_x += 0.5 * padding_width
        div_x = np.repeat(div_x, 2)
        div_y = np.full((division, 2), [0, -height_division])
        self.division = np.vstack((div_x, div_y.reshape(-1))).transpose()

        self.subdivision = None
        if subdivision > 0:
            subdiv_x = np.array([
                np.linspace(div_x[2 * i], div_x[2 * i + 2], subdivision + 2)[1:-1]
                for i in range(division - 1)
            ])
            subdiv_x = np.repeat(subdiv_x.reshape(-1), 2)
            subdiv_y = np.full(
                ((division - 1) * subdivision, 2), [0, -height_subdivision]
            )
            self.subdivision = np.vstack((subdiv_x, subdiv_y.reshape(-1))).transpose()

        self.move_to(np.array([0, 0]))

    @property
    def start(self):
        return self.division[0]

    @property
    def end(self):
        return self.division[-2]

    def _angle_vec(self, vec1: np.ndarray, vec2: np.ndarray):
        return np.arctan2(vec2[1], vec2[0]) - np.arctan2(vec1[1], vec1[0])

    def _get_division(self, div: int, subdiv: int = None):
        div, subdiv = 2 * div, 2 * subdiv if subdiv is not None else None
        if div >= len(self.division):
            raise IndexError("division index out of range")
        if subdiv is None:
            return self.division[div]
        if self.subdivision is None:
            raise ValueError("subdivision is not defined")

        count_subdiv = len(self.subdivision) // (len(self.division) - 2)

        if subdiv >= 2 * count_subdiv:
            raise IndexError("subdivision index out of range")

        return self.subdivision[count_subdiv * div + subdiv]

    def rotate_about_point(self, angle: float, point: np.ndarray):
        rot_mat = np.array([
            [np.cos(angle), np.sin(angle)], 
            [-np.sin(angle), np.cos(angle)]
        ])
        self.shape = np.matmul(self.shape - point, rot_mat) + point
        self.division = np.matmul(self.division - point, rot_mat) + point
        if self.subdivision is not None:
            self.subdivision = np.matmul(self.subdivision - point, rot_mat) + point

    def rotate_about_start(self, angle: float):
        self.rotate_about_point(angle, self.start)

    def rotate_about_end(self, angle: float):
        self.rotate_about_point(angle, self.end)

    def rotate_about_division(
        self, angle: float, division: int, subdivision: int = None
    ):
        self.rotate_about_point(angle, self._get_division(division, subdivision))

    def rotate_start_to(self, point: np.ndarray):
        angle = self._angle_vec(self.start - self.end, point - self.end)
        self.rotate_about_end(angle)
        product = np.dot(self.start - point, self.end - point)

        if not np.isclose(product, 0) and product > 0:
            raise ValueError("can't rotate to chosen point")

    def rotate_end_to(self, point: np.ndarray):
        angle = self._angle_vec(self.end - self.start, point - self.start)
        self.rotate_about_start(angle)
        product = np.dot(self.start - point, self.end - point)

        if not np.isclose(product, 0) and product > 0:
            raise ValueError("can't rotate to chosen point")

    def shift(self, vec: np.ndarray):
        self.shape += vec
        self.division += vec

        if self.subdivision is not None:
            self.subdivision += vec

    def move_to(self, point: np.ndarray):
        vec = 0.25 * np.sum(self.shape, axis=0)
        self.shift(point - vec)

    def move_start_to(self, point: np.ndarray):
        self.shift(point - self.start)

    def move_end_to(self, point: np.ndarray):
        self.shift(point - self.end)

    def move_division_to(
        self, point: np.ndarray, division: int, subdivision: int = None
    ):
        self.shift(point - self._get_division(division, subdivision))

Функции пересечений

При построении циркулем и линейкой нужно находить точки пересечений окружностей и прямых, поэтому напишем три функции, которые это делают.

Первая функция — пересечение прямых. На вход она получает две прямые в виде двух точек, через которые проходит прямая. На выходе же возвращает точку пересечения или None, если прямые не пересекаются.

Эту функцию можно написать по-разному. Самый простой способ - в лоб решить систему уравнений, но я нашёл более красивый способ. Я не очень хочу объяснять, почему это так, потому что для этого придётся лезть в проективную геометрию, и к тому же по ссылке есть хорошее объяснение этого.

def line_intersection(
    line1: tuple[np.ndarray, np.ndarray], line2: tuple[np.ndarray, np.ndarray]
):
    s = np.vstack((line1, line2))
    h = np.hstack((s, np.ones((4, 1))))
    line1 = np.cross(h[0], h[1])
    line2 = np.cross(h[2], h[3])
    x, y, z = np.cross(line1, line2)

    if np.isclose(z, 0):
        return None

    return np.array([x / z, y / z])

Вторая функция — пересечение прямой и окружности. На вход она получает прямую в виду двух точек и окружность в виде координат центра и радиуса. На выходе же возвращает точки пересечения или None, если их нет.

Тут придётся решать систему уравнений, но я нашёл уже готовые формулы. Можно заметить, что они верны только для случая, когда окружность находится в начале координат. Поэтому в общем случае, нужно сначала сдвинуть прямую и окружность так, чтобы центр окружности попал в начало координат, воспользоваться формулами и обратно сдвинуть полученные точки пересечения.

def circle_line_intersection(
    line: tuple[np.ndarray, np.ndarray], circle: tuple[np.ndarray, float]
):
    center, radius = circle
    p1, p2 = line - center
    dx = p2[0] - p1[0]
    dy = p2[1] - p1[1]
    dr = dx**2 + dy**2
    det = p1[0] * p2[1] - p1[1] * p2[0]
    d = dr * radius**2 - det**2

    if np.isclose(d, 0):
        return np.array([det * dy / dr, -det * dx / dr]) + center
    elif d > 0:
        x1 = (det * dy + dx * np.sqrt(d)) / dr
        y1 = (-det * dx + dy * np.sqrt(d)) / dr
        x2 = (det * dy - dx * np.sqrt(d)) / dr
        y2 = (-det * dx - dy * np.sqrt(d)) / dr
        return np.array([x1, y1]) + center, np.array([x2, y2]) + center
      
    return None

Последняя функция — пересечение двух окружностей. На вход она получает две окружности в виде центра координат и радиуса. На выходе же возвращает точки пересечения или None, если их нет.

И опять таки я нашёл уже готовое решение. Суть его в следующем. Для того, чтобы найти точки пересечения окружностей, нужно решить такую систему

$\left \{\begin{array}{l} (x-x_0)^2 + (y-y_0)^2 = r^2, \\ (x-\widetilde{x}_0)^2 + (y-\widetilde{y}_0)^2 = \widetilde{r}^2. \end{array} \right.$

Если первая окружность не находится в начале координат, то сдвинем окружности так, чтобы центр попал в начало координат.

$\left \{\begin{array}{l} x^2 + y^2 = r^2, \\ (x + (x_0-\widetilde{x}_0))^2 + (y- (y_0 - \widetilde{y}_0))^2 = \widetilde{r}^2. \end{array} \right.$

Вычтем первое уравнение из второго

$\left \{\begin{array}{l} x^2 + y^2 = r^2, \\ 2x(x_0-\widetilde{x}_0) + 2y(y_0 - \widetilde{y}_0) - (x_0 - \widetilde{x}_0)^2 - (y_0 - \widetilde{y}_0)^2 - \widetilde{r}^2 = 0 .\end{array} \right.$

А теперь осталось заметить, что второе уравнение — это уравнение прямой. То есть поиск точек пересечений двух окружностей сводится к поиску точек пересечений прямой и окружности.

def circle_intersection(
    circle1: tuple[np.ndarray, float], circle2: tuple[np.ndarray, float]
):
    center1, radius1 = circle1
    center2, radius2 = circle2
    new_center = center1 - center2
    a = 2 * new_center[0]
    b = 2 * new_center[1]
    c = new_center[0] ** 2 + new_center[1] ** 2 + radius1**2 - radius2**2

    if np.isclose(a, 0):
        line = np.array([0, -c / b]), np.array([1, -c / b])
    elif np.isclose(b, 0):
        line = np.array([-c / a, 0]), np.array([-c / a, 1])
    else:
        line = np.array([-1, (a - c) / b]), np.array([0, -c / b])

    points = circle_line_intersection(line, (np.array([0, 0]), radius1))
    return points + center1 if points is not None else None

Полный код функций пересечений

import numpy as np


def line_intersection(
    line1: tuple[np.ndarray, np.ndarray], line2: tuple[np.ndarray, np.ndarray]
):
    s = np.vstack((line1, line2))
    h = np.hstack((s, np.ones((4, 1))))
    line1 = np.cross(h[0], h[1])
    line2 = np.cross(h[2], h[3])
    x, y, z = np.cross(line1, line2)

    if np.isclose(z, 0):
        return None

    return np.array([x / z, y / z])


def circle_intersection(
    circle1: tuple[np.ndarray, float], circle2: tuple[np.ndarray, float]
):
    center1, radius1 = circle1
    center2, radius2 = circle2
    new_center = center1 - center2
    a = 2 * new_center[0]
    b = 2 * new_center[1]
    c = new_center[0] ** 2 + new_center[1] ** 2 + radius1**2 - radius2**2

    if np.isclose(a, 0):
        line = np.array([0, -c / b]), np.array([1, -c / b])
    elif np.isclose(b, 0):
        line = np.array([-c / a, 0]), np.array([-c / a, 1])
    else:
        line = np.array([-1, (a - c) / b]), np.array([0, -c / b])

    points = circle_line_intersection(line, (np.array([0, 0]), radius1))

    return points + center1 if points is not None else None


def circle_line_intersection(
    line: tuple[np.ndarray, np.ndarray], circle: tuple[np.ndarray, float]
):
    center, radius = circle
    p1, p2 = line - center
    dx = p2[0] - p1[0]
    dy = p2[1] - p1[1]
    dr = dx**2 + dy**2
    det = p1[0] * p2[1] - p1[1] * p2[0]
    d = dr * radius**2 - det**2

    if np.isclose(d, 0):
        return np.array([det * dy / dr, -det * dx / dr]) + center
    elif d > 0:
        x1 = (det * dy + dx * np.sqrt(d)) / dr
        y1 = (-det * dx + dy * np.sqrt(d)) / dr
        x2 = (det * dy - dx * np.sqrt(d)) / dr
        y2 = (-det * dx - dy * np.sqrt(d)) / dr

        return np.array([x1, y1]) + center, np.array([x2, y2]) + center

    return None

Заключение

На этом первая часть закончена. Но уже во второй части будет показано, как от всего этого перейти к анимации.

Если у вас есть какие-нибудь идеи, что можно ещё добавить, или я что-то написал плохо, то обязательно пишите, я это всё учту.

Различные ссылки

Tags:

Hubs: