Задание: необходимо создать кодовое слово, состоящее из 8 цифр (на примере – 01234567) на основе алгоритма, частично приведенного в ГОСТ Р ИСО/МЭК 18004-2015 (п. 7.4.3, пример 2). Затем создать для полученного кода Micro QR Code вер. М2. Данный режим невозможно прочитать стандартными ресурсами мобильных устройств, производимых GAFAM (как оказалось, свободно распространяемые библиотеки просто страшно глючат, поэтому ассоциация отказалась от этого режима).
Примечание: первая часть приведенного ниже алгоритма (до Таблицы 2) будет полностью дублировать предыдущий по ГОСТ вариант.
Этап 1. Кодирование исходных данных
Рассмотрим М2 поближе. Имеем матрицу размерностью 13x13 бинарных символов, один индикатор и два определителя (горизонтальный и вертикальный) (рис. 1).

Примечание: здесь и далее будем использовать один из доступных программных инструментов практически на любом ПК – MS Excel (русскоязычная версия). Как следствие, все команды автоматизации процессов будут на кириллице.
Примечание: здесь и далее будет использоваться информация ГОСТ Р ИСО/МЭК 18004-2015 или в оригинале ISO/IEC 18004:2015 (далее – ГОСТ).
Первый наносимый ограничитель символ на матрицу М2 – битовая последовательность информации о формате (рис. 2). Чтение битовой последовательности начинается с 14 бита, т.е. последовательность чтения/записи будет 14, 13, 12, 11, 10 и т.д.

Примечание: этап заполнения битовой последовательности информации о формате кодовой битовой комбинацией в представленном алгоритме будет пятым, после определения маски.
Второй не менее важный элемент М2 – маршрут последовательности заполнения битами данных поля матрицы (рис. 3). Данная схема отражена на рисунке 11 ГОСТ.
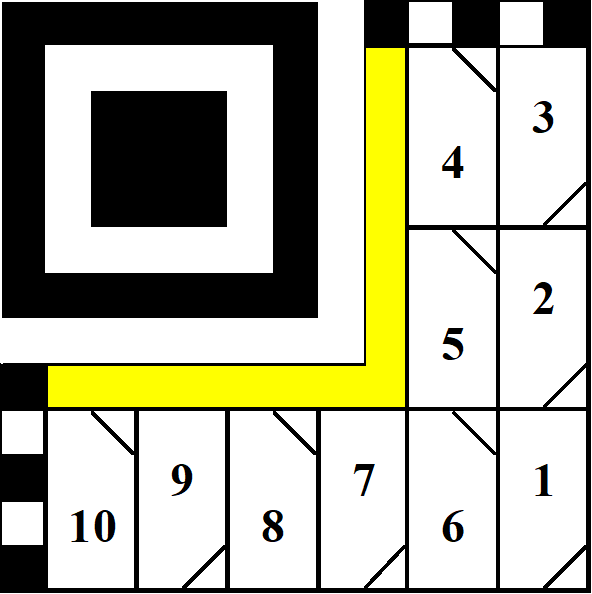
Если наложить маршрут на матрицу, получаем последовательность из 80 бит кода М2 (рис. 4). Число 80 пригодится чуть позже при работе с кодами Рида-Соломона.

Переходим к реализации первого этапа – получение кодовой комбинации исходного текста. В системе QR Code существует несколько разновидностей кодирования: числовой, алфавитно-цифровой, байтовый, кандзи, структурированное соединение и FNC1. Самые простые – числовой (число определенной длины из цифр 0..9) и алфавитно-цифровой (табл. 1).
Таблица 1 – Кодирование/декодирование для алфавитно-цифрового режима (Таблица 5 ГОСТ)
Знак | Значение | Знак | Значение | Знак | Значение | Знак | Значение | Знак | Значение | Знак | Значение | Знак | Значение | Знак | Значение |
0 | 0 | 6 | 6 | С | 12 | I | 18 | О | 24 | U | 30 | SP | 36 | . | 42 |
1 | 1 | 7 | 7 | D | 13 | J | 19 | Р | 25 | V | 31 | $ | 37 | / | 43 |
2 | 2 | 8 | 8 | Е | 14 | К | 20 | Q | 26 | W | 32 | % | 38 | : | 44 |
3 | 3 | 9 | 9 | F | 15 | L | 21 | R | 27 | X | 33 | * | 39 |
|
|
4 | 4 | А | 10 | G | 16 | М | 22 | S | 28 | Y | 34 | + | 40 |
|
|
5 | 5 | В | 11 | Н | 17 | N | 23 | Т | 29 | Z | 35 | - | 41 |
|
|
В данной таблице есть одна особенность – используется исключительно латиница верхн��го регистра, т.е. большие буквы.
Примечание: каждый из методов имеет ряд собственных особенностей. Не получится использовать предложенный ниже алгоритм для чисел или для байтовых последовательностей.
Используем числовую систему кодирования для выполнения требований задания. Следующее ограничение – необходимо кодировать ровно 8 цифровых символов. М2 поддерживает два уровня исправления ошибок – L и M. Обращаемся к таблице 7 ГОСТ, получаем, что уровни L и M поддерживают емкость 8 цифровых символов (табл. 2, емкость данных для цифрового режима). Более оптимальный – уровень М, но в ГОСТ выбран уровень L (сделаем в разрез с ГОСТ, выбираем уровень М). Выбор уровня исправления ошибок М будет отражен позже на пятом этапе в надлежащей битовой последовательности информации о формате (рис. 2).
Таблица 2 – Число знаков символа и емкость входных данных для QR Code (Таблица 7 ГОСТ)
Версия | Уровень исправления ошибок | Число кодовых слов данных | Число битов для данных | Емкость данных для разных режимов | |||
Цифровой | Алфавитно-цифровой | Байтовый | Кандзи | ||||
М1 | Только обнаружение ошибок | 3 | 20 | 5 | - | - | - |
М2 | L | 5 | 40 | 10 | 6 | - | - |
М | 4 | 32 | 8 | 5 | - | - | |
М3 | L | 11 | 84 | 23 | 14 | 9 | 6 |
М | 9 | 68 | 18 | 11 | 7 | 4 | |
М4 | L | 16 | 128 | 35 | 21 | 15 | 9 |
М | 14 | 112 | 30 | 18 | 13 | 8 | |
Q | 10 | 80 | 21 | 13 | 9 | 5 | |
Воспользуемся алгоритмом, представленном в ГОСТ (п. 7.4.3). Разбиваем строку на группы по три цифры и преобразуем каждую группу из десятичного числа в 10-битовый двоичный эквивалент для трех цифр, в 7-битовый двоичный эквивалент для двух цифр и в 4-битовый двоичный эквивалент для одной цифры. Для данного примера получаем:
012 → 0000001100;
345 → 0101011001;
67 → 1000011;
Создадим в MS Excel новый пустой Лист. Пример готового результата представлен на рисунке 5.
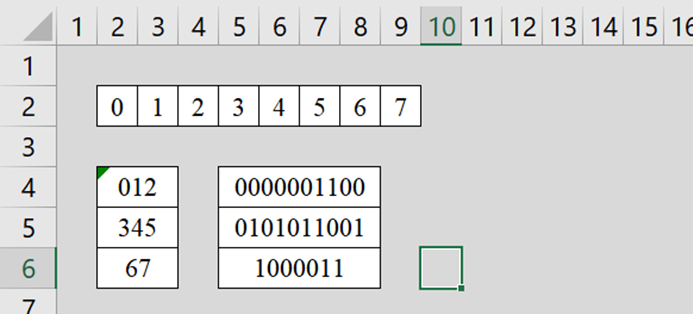
Для автоматизации первого этапа сначала переносим таблицу набор цифр, начиная с ячейки (2, 2). Резервируем 4 строчку, начиная с ячейки (4, 2) для исходных данных. Объединяем ячейки (4, 2) и (4, 3). Добавляем функцию:
=R[-2]C&R[-2]C[1]&R[-2]C[2]
В строке 4 объединяем ячейки с 5 по 8. В ячейку (4,5) добавляем функцию:
=ДЕС.В.ДВ(RC[-3];10)
Аналогично заполняем ячейки в строках 5 и 6:
Ячейка | Значение |
(5, 2)-(5, 3) | =R[-3]C[3]&R[-3]C[4]&R[-3]C[5] |
(5, 5)-(5, 8) | =ДЕС.В.ДВ(RC[-3];10) |
(6, 2)-(6, 3) | =R[-4]C[6]&R[-4]C[7] |
(6, 5)-(6, 8) | =ДЕС.В.ДВ(RC[-3];7) |
Далее необходимо объединить все три полученные бинарные кодовые последовательности в одну. В 8 строке объединяем ячейки с 2 по 12. В ячейку (8, 2) добавляем:
=R[-4]C[3]&R[-3]C[3]&R[-2]C[3]
Полученная кодовая комбинация (рис. 6):
000000110001010110011000011

К полученной кодовой комбинации необходимо добавить служебную информацию: индикатор цифрового режима для вер. М2 и число знаков (в данном случае 8 знаков – 01234567). Воспользуемся таблицами 2 и 3 ГОСТ. В таблице индикаторов режима (табл. 3) определяем, что индикатор цифрового режима для вер. М2 – 0. В таблице числа битов в индикаторе числа знаков (табл. 4) определяем, что выделяется четыре бита на описание числа знаков, т.е. число 8 будет представлено как 1000.
Таблица 3 – Индикаторы режима для QR Code (Таблица 2 ГОСТ)
Режим | Символы QR Code | Символы Micro QR Code | |||
версия | любой версии | М1 | М2 | М3 | M4 |
Длина индикатора режима, биты | 4 | 0 | 1 | 2 | 3 |
ECI | 0111 | n/a | n/a | n/a | n/a |
Числовой | 0001 | n/a | 0 | 00 | 000 |
Алфавитно-цифровой | 0010 | n/a | 1 | 01 | 001 |
Байтовый | 0100 | n/a | n/a | 10 | 010 |
Кандзи | 1000 | n/a | n/a | 11 | 011 |
Структурированное соединение | 0011 | n/a | n/a | n/a | n/a |
FNC1a | 0101 (1-я позиция) | n/a | n/a | n/a | n/a |
1001 (2-я позиция) | |||||
Ограничитель (конец сообщения) | 0000 | 000 | 00000 | 0000000 | 000000000 |
Таблица 4 – Число битов в индикаторе числа знаков для QR Code (Таблица 3 ГОСТ)
Версия | Числовой режим | Алфавитно-цифровой режим | Байтовый режим | Режим кандзи |
M1 | 3 | n/a | n/a | n/a |
М2 | 4 | 3 | n/a | n/a |
М3 | 5 | 4 | 4 | 3 |
M4 | 6 | 5 | 5 | 4 |
1-9 | 10 | 9 | 8 | 8 |
10-26 | 12 | 11 | 16 | 10 |
27-40 | 14 | 13 | 16 | 12 |
Для проверки воспользуемся функцией (рис. 7). В ячейку (11, 11)-(11, 12) добавляем функцию:
=ДЕС.В.ДВ(RC[-1];4)

Объединяем служебную информацию и исходный код в единую последовательность:
0 1000 000000110001010110011000011
Объединяем ячейки (13, 2)-(13, 13). В полученную ячейку (13, 2) добавляем код:
=R[-3]C[8]&R[-2]C[9]&R[-5]C
Результат формирования текущей битовой последовательности представлен на рисунке 8.

Для дальнейшей работы с кодами Рида-Соломона (2 этап) необходимо сделать полученную последовательность из 4 символов (табл. 2, число кодовых слов данных для режима M2-М равно 4) по количеству символов кратной 8, т.е. при необходимости добавить биты ограничители (по табл. 3, максимальное количество для М2 равно пяти нулям) и биты заполнители. В текущей битовой последовательности в ячейке (13, 2) ровно 32 символа, что кратно 8 (рис. 10):
01000000000110001010110011000011
Повторно проверяем по таблице 2 (ГОСТ Таблица 7) насколько получилась правильная комбинация. Напротив строки M2-М в столбце «Число кодовых слов данных» указано число 4, т.е. должно получиться 4 части по 8 бит – 01000000 00011000 10101100 11000011. Следовательно, полученная последовательность полностью соответствует требованиям ГОСТ.
Для разделения итоговой битовой комбинации на четыре 8-битных последовательностей воспользуемся командой =ПСТР(ссылка на ячейку; позиция первого символа; количество бит). Получаем следующие комбинации (рис. 10):
Диапазон ячеек | Значение |
(10, 15)-(10, 19) | =ПСТР(R[3]C[-13];1;8) |
(11, 15)-(11, 19) | =ПСТР(R[2]C[-13];9;8) |
(12, 15)-(12, 19) | =ПСТР(R[1]C[-13];17;8) |
(13, 15)-(13, 19) | =ПСТР(C[-13];25;8) |
Для визуализации полученного результата, перенесем полученную битовую комбинацию в шаблон Micro QR Code вер. М2 (рис. 9).


Для перехода ко 2 этапу необходимо перевести полученные 8-битовые комбинации в десятичный вид. Воспользуемся командой =ДВ.В.ДЕС(ссылка на ячейку), получаем последовательность чисел (рис. 10):
64, 24, 172, 195
Диапазон ячеек | Значение |
(10, 20)-(10, 21) | =ДВ.В.ДЕС(RC[-5]) |
(11, 20)-(11, 21) | =ДВ.В.ДЕС(RC[-5]) |
(12, 20)-(12, 21) | =ДВ.В.ДЕС(RC[-5]) |
(13, 20)-(13, 21) | =ДВ.В.ДЕС(RC[-5]) |

Итак, итоговая комбинация: 64, 24, 172, 195. Можно переходить ко 2 этапу.
Этап 2. Генерация кодовых слов исправления ошибок
Для генерации кодовых слов исправления ошибок необходимо использовать алгоритм Рида-Соломона на поле Галуа GF(28).
Примечание: для самых любопытных, если интересно посмотреть с точки зрения алгебры множеств то, что будет описываться дальше на примере в таблице MS Excel, можно посмотреть/изучить достаточно хороший материал на Хабр:
[2] Кодирование Рида-Соломона для чайников
[3] Арифметика полей Галуа для кодирования информации кодами Рида-Соломона
В данном материале математику изучать не будет, но будем применять во всей красоте магии чисел.
Создаем новый Лист в Книге MS Excel. Забегая вперед, демонстрация результата (рис. 11).

Для деления полиномов будем использовать поле Галуа GF(28) и обратное поле Галуа GF(28) – обязательное требование при работе с QR Code в ГОСТ. Можно просто переписать большую таблицу значений в ячейки, но предполагалась автоматизация. Следовательно, воспользуемся простыми функциями для создания полей.
Поле Галуа GF(28) представляет фиксированный набор из 256 чисел в диапазоне от 0 до 255. Сначала зададим простой ряд натуральных чисел от 0 до 255 в строке 2. В ячейке (2, 2) – 0, в (2, 3) – 1, в (2, 4) – 2 и т.д. до ячейки (2, 257) – 255. Заполняем третью строку. Первая часть идет с простыми значениями:
Ячейка | Значение |
(3, 2) | 1 |
(3, 3) | 2 |
(3, 4) | =RC[-1]*2 |
(3, 5) | =RC[-1]*2 |
(3, 6) | =RC[-1]*2 |
(3, 7) | =RC[-1]*2 |
(3, 8) | =RC[-1]*2 |
(3, 9) | =RC[-1]*2 |
На этом простая часть закончилась, дальше чуть посложнее. Начиная с ячейки (3, 10) необходимо во все последующие ячейки до (3, 257) добавить следующую функцию:
=ЕСЛИ(2*RC[-1]>254;БИТ.ИСКЛИЛИ(2*RC[-1];285);RC[-1]*2)
где добавлено условие: если значение из предыдущей ячейки умноженное на 2 превышает 254, то необходимо выполнить XOR с числом 285. Почему именно 285 описано в статьях по ссылкам выше. Если число меньше 254, то просто оставляем в текущей ячейке умноженное на 2 полученное значение.
Для контроля полученного результата можно воспользоваться рисунком 11.
Обратное поле Галуа GF(28) аналогично представляет фиксированный набор из 256 чисел в диапазоне от 0 до 255. Сначала зададим простой ряд натуральных чисел от 0 до 255 в шестой строке. В ячейке (6, 2) – 0, в (6, 3) – 1, в (6, 4) – 2 и т.д. до ячейки (6, 257) – 255. Заполняем седьмую строку. В ячейке (7, 2) – ставим прочерк. Данного значения не существует. Ячейки (7, 3) – (7, 257) заполняем функцией:
=ИНДЕКС(R2C2:R2C257;ПОИСКПОЗ(R[-1]C;R3C2:R3C257;0))
где производится поиск по индексу шестой строки соответствующего значения в поле Галуа GF(28). Для контроля полученного результата также можно воспользоваться рисунком 11. В результате оба поля должны быть созданы в полном объеме.
Переходим к основному действию – деление полиномов. Сначала необходимо определить уровень корректирующего полинома. На первом этапе получили максимальное количество бит на поле М2 (рис. 4) – 80 бит. Далее определили последовательность бит исходных данных со служебной информацией (рис. 10) – 4 значения по 8 бит (итого – 32). Следовательно, корректирующий код исправления ошибок должен состоять из 48 бит ( бит) или 6 чисел по 8 бит. И здесь начинаются странности с ГОСТ.
Примечание: не ищите в ГОСТ алгоритма определения необходимого количества бит корректирующего кода исправления ошибок. В оригинале ISO тоже нет.
Примечание: все необходимые коэффициенты полиномов можно найти в форме степеней в приложении А ГОСТ, таблица А.1. Но в ГОСТ не описан механизм применения.
Обращаемся к таблице А.1 ГОСТ. Полином 6 уровня имеет коэффициенты 166, 0, 134, 5, 176, 15.
Все необходимые исходные данные для деления полиномов готовы, переходим к практической составляющей.
Примечание: разные комбинации (длина битовой комбинации исходных данных больше длины битовой комбинации корректирующего полинома или длина битовой комбинации исходных данных меньше длины битовой комбинации корректирующего полинома) имеют разные алгоритмы реализации. Далее будет описан алгоритм, когда длины корректирующего полинома больше.
Возвращаемся к битовой комбинации исходных данных (рис. 10). И переносим в ячейки текущего Листа Книги MS Excel (рис. 11):
Ячейка | Значение |
(13, 24) | 64 |
(13, 25) | 24 |
(13, 26) | 172 |
(13, 27) | 195 |
Заполняем 15 строку значениями (коэффициентами) корректирующего полинома (рис. 11):
Ячейка | Значение |
(15, 24) | 166 |
(15, 25) | 0 |
(15, 26) | 134 |
(15, 27) | 5 |
(15, 28) | 176 |
(15, 29) | 15 |
Каждый этап деления будет состоять из 4 последовательных шагов. Каждый шаг будет описан отдельно. Переходим на 16 строку. Ячейка (16, 23):
=ИНДЕКС(R7C2:R7C257;ПОИСКПОЗ(R[-3]C[1];R6C2:R6C257;0))
где ищем значение первого числа исходного кода (64) в обратном поле Галуа GF(28). Получаем результат – 6.
В ячейки (16, 24)-(16, 29) прописываем следующую функцию:
=ОСТАТ(R[-1]C+R16C23;255)
В результате получаем ряд чисел:
172, 6, 140, 11, 182, 21
Переходим к 17 строке. Ячейки (17, 23)-(17, 29) заполняем следующей функцией:
=ИНДЕКС(R3C2:R3C257;ПОИСКПОЗ(R[-1]C;R2C2:R2C257;0))
В результате получаем ряд чисел:
64, 123, 64, 132, 232, 98, 117
Переходим к 18 строке. Ячейки (18, 23)-(18, 29) заполняем следующей функцией:
=R[-5]C[1]
В результате получаем ряд чисел:
64, 24, 172, 195, 0, 0, 0
Переходим к 19 строке. Ячейки (19, 23)-(19, 29) заполняем следующей функцией:
=БИТ.ИСКЛИЛИ(R[-2]C;R[-1]C)
В результате получаем ряд чисел:
0, 99, 236, 71, 232, 98, 117
Первый этап деления выполнен. Все 4 шага описаны. Всего количество этапов будет 4 – по количеству значений исходного кода.
Переходим на 20 строку. Ячейка (20, 23):
=ИНДЕКС(R7C2:R7C257;ПОИСКПОЗ(R[-1]C[1];R6C2:R6C257;0))
где ищем значение первого числа переходного кода (99) в обратном поле Галуа GF(28). Получаем результат – 163.
В ячейки (20, 24)-(20, 29) прописываем следующую функцию:
=ОСТАТ(R15C+R20C23;255)
В результате получаем ряд чисел:
74, 163, 42, 168, 84, 178
Переходим к 21 строке. Ячейки (21, 23)-(21, 29) заполняем следующей функцией:
=ИНДЕКС(R3C2:R3C257;ПОИСКПОЗ(R[-1]C;R2C2:R2C257;0))
В результате получаем ряд чисел:
99, 137, 99, 181, 252, 107, 171
Переходим к 22 строке. Ячейки (22, 23)-(22, 29) заполняем следующей функцией:
=R[-3]C[1]
В результате получаем ряд чисел:
89, 236, 71, 232, 98, 117, 0
Переходим к 23 строке. Ячейки (23, 23)-(23, 29) заполняем следующей функцией:
=БИТ.ИСКЛИЛИ(R[-2]C;R[-1]C)
В результате получаем ряд чисел:
0, 101, 36, 93, 158, 30, 171
Второй этап деления выполнен.
Переходим на 24 строку. Ячейка (24, 23):
=ИНДЕКС(R7C2:R7C257;ПОИСКПОЗ(R[-1]C[1];R6C2:R6C257;0))
где ищем значение первого числа переходного кода (101) в обратном поле Галуа GF(28). Получаем результат – 72.
В ячейки (24, 24)-(24, 29) прописываем следующую функцию:
=ОСТАТ(R15C+RC23;255)
В результате получаем ряд чисел:
238, 72, 206, 77, 248, 87
Переходим к 25 строке. Ячейки (25, 23)-(25, 28) заполняем следующей функцией:
=ИНДЕКС(R3C2:R3C257;ПОИСКПОЗ(R[-1]C;R2C2:R2C257;0))
В результате получаем ряд чисел:
101, 11, 101, 83, 60, 27, 127
Переходим к 26 строке. Ячейки (26, 23)-(26, 29) заполняем следующей функцией:
=R[-3]C[1]
В результате получаем ряд чисел:
101, 36, 93, 158, 30, 171, 0
Переходим к 27 строке. Ячейки (27, 23)-(27, 29) заполняем следующей функцией:
=БИТ.ИСКЛИЛИ(R[-2]C;R[-1]C)
В результате получаем ряд чисел:
0, 47, 56, 205, 34, 176, 127
Третий этап деления выполнен.
Переходим на 28 строку. Ячейка (28, 23):
=ИНДЕКС(R7C2:R7C257;ПОИСКПОЗ(R[-1]C[1];R6C2:R6C257;0))
где ищем значение первого числа переходного кода (47) в обратном поле Галуа GF(28). Получаем результат – 69.
В ячейки (28, 24)-(28, 29) прописываем следующую функцию:
=ОСТАТ(R15C+RC23;255)
В результате получаем ряд чисел:
235, 69, 203, 74, 245, 84
Переходим к 29 строке. Ячейки (29, 23)-(29, 29) заполняем следующей функцией:
=ИНДЕКС(R3C2:R3C257;ПОИСКПОЗ(R[-1]C;R2C2:R2C257;0))
В результате получаем ряд чисел:
47, 235, 47, 224, 137, 233, 107
Переходим к 30 строке. Ячейки (30, 23)-(30, 29) заполняем следующей функцией:
=R[-3]C[1]
В результате получаем ряд чисел:
47, 56, 205, 34, 176, 127, 0
Переходим к 31 строке. Ячейки (31, 23)-(31, 29) заполняем следующей функцией:
=БИТ.ИСКЛИЛИ(R[-2]C;R[-1]C)
В результате получаем ряд чисел:
0, 211, 226, 194, 57, 150, 107
Заключительный четвертый этап деления выполнен.
Итак, вторая часть битовой комбинации кода получена. Далее необходимо первую и вторую часть перевести в двоичную комбинацию и получить итоговую битовую последовательность.
Переносим две исходные последовательности в столбики в ячейки:
Ячейка | Значение | Ячейка | Значение |
(16, 4)-(16, 5) | 64 | (16, 13)-(16, 14) | 211 |
(17, 4)-(17, 5) | 24 | (17, 13)-(17, 14) | 226 |
(18, 4)-(18, 5) | 172 | (18, 13)-(18, 14) | 194 |
(19, 4)-(19, 5) | 195 | (19, 13)-(19, 14) | 57 |
|
| (20, 13)-(20, 14) | 150 |
|
| (21, 13)-(21, 14) | 107 |
Получаем два столбика двоичных последовательностей (рис. 11):
Ячейка | Значение | Ячейка | Значение |
(16, 4)-(16, 5) | =ДЕС.В.ДВ(RC[-3];8) | (16, 13)-(16, 14) | =ДЕС.В.ДВ(RC[-3];8) |
(17, 4)-(17, 5) | =ДЕС.В.ДВ(RC[-3];8) | (17, 13)-(17, 14) | =ДЕС.В.ДВ(RC[-3];8) |
(18, 4)-(18, 5) | =ДЕС.В.ДВ(RC[-3];8) | (18, 13)-(18, 14) | =ДЕС.В.ДВ(RC[-3];8) |
(19, 4)-(19, 5) | =ДЕС.В.ДВ(RC[-3];8) | (19, 13)-(19, 14) | =ДЕС.В.ДВ(RC[-3];8) |
|
| (20, 13)-(20, 14) | =ДЕС.В.ДВ(RC[-3];8) |
|
| (21, 13)-(21, 14) |
|
В 23 строке объединяем ячейки (23, 3)-(23, 10) и (23, 11)-(23, 20). В ячейку (23, 3) добавляем функцию:
=R[-7]C[4]&R[-6]C[4]&R[-5]C[4]&R[-4]C[4]
И в ячейку (23, 11) добавляем функцию:
=R[-7]C[5]&R[-6]C[5]&R[-5]C[5]&R[-4]C[5]&R[-3]C[5]&R[-2]C[5]
В 25 строке объединяем ячейки (25, 3)-(25, 20). В ячейку (25, 3) добавляем функцию:
=R[-2]C&R[-2]C[8]
Пример итогового варианта представлен на рисунке 12.

Этап 3. Размещение модулей в матрице символа
Шаблон поиска и шаблоны синхронизации размещают в пустой матрице 13×13, а модули в позиции для информации о формате временно оставляют пустыми. Кодовые слова, полученные на этапах 1 и 2 (табл. 5), размещают в матрице в соответствии с п. 7.7.3 ГОСТ, в результате получают символ, приведенный на рис. 13.
Таблица 5 – Кодовые слова
1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 | 12 | 13 | 14 | 15 | 16 | 17 | 18 | 19 | 20 |
0 | 1 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 1 | 1 | 0 | 0 | 0 | 1 | 0 | 1 | 0 |
21 | 22 | 23 | 24 | 25 | 26 | 27 | 28 | 29 | 30 | 31 | 32 | 33 | 34 | 35 | 36 | 37 | 38 | 39 | 40 |
1 | 1 | 0 | 0 | 1 | 1 | 0 | 0 | 0 | 0 | 1 | 1 | 1 | 1 | 0 | 1 | 0 | 0 | 1 | 1 |
41 | 42 | 43 | 44 | 45 | 46 | 47 | 48 | 49 | 50 | 51 | 52 | 53 | 54 | 55 | 56 | 57 | 58 | 59 | 60 |
1 | 1 | 1 | 0 | 0 | 0 | 1 | 0 | 1 | 1 | 0 | 0 | 0 | 0 | 1 | 0 | 0 | 0 | 1 | 1 |
61 | 62 | 63 | 64 | 65 | 66 | 67 | 68 | 69 | 70 | 71 | 72 | 73 | 74 | 75 | 76 | 77 | 78 | 79 | 80 |
1 | 0 | 0 | 1 | 1 | 0 | 0 | 1 | 0 | 1 | 1 | 0 | 0 | 1 | 1 | 0 | 1 | 0 | 1 | 1 |

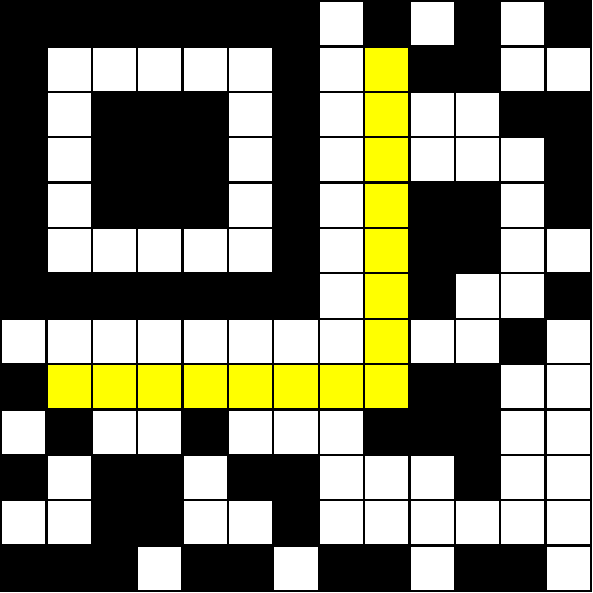
Этап 4. Выбор шаблона маски данных
Для выбора наиболее удачного варианта применяются шаблоны маски данных согласно п. 7.8.2 ГОСТ по очереди и оценивают результаты по п. 7.8.3 ГОСТ. Рассмотрим последовательно описанный в пунктах ГОСТ процесс для данного примера. Создаем новый Лист в Книге MS Excel.
На рисунке 22 ГОСТ представлены маски для Micro QR Code, вычисляемые по формулам таблицы 10 ГОСТ (табл. 6).
Таблица 6 – Условия генерации шаблона маски данных
Указатель шаблона маски данных для символов QR Code | Указатель шаблона маски данных для символов Micro QR Code | Условие |
000 |
| (i + j) mod 2 = 0 |
001 | 00 | i mod 2 = 0 |
010 |
| j mod 3 = 0 |
011 |
| (i + j) mod 3 = 0 |
100 | 01 | ((i div 2) + (j div 3)) mod 2 = 0 |
101 |
| (ij) mod 2 + (ij) mod 3 = 0 |
110 | 10 | ((ij) mod 2 + (ij) mod 3) mod 2 = 0 |
111 | 11 | ((i + j) mod 2 + (i + j) mod 3) mod 2 = 0 |
Можно процесс наполнения масок бинарными данными автоматизировать, но в данной постановке решено пропустить этап и заполнить маски вручную. Для любопытных, подсказка, как можно автоматизировать (рис. 14).

Переносим указанные в табл. 6 маски на новый Лист MS Excel (рис. 15).

Примечание: MS Excel не умеет работать с цветами ячеек. Для дальнейшей автоматизации во всех ячейках масок белые биты подписаны нулями (0), черные – единицами (1).
Бинарную матрицу предыдущего этапа (рис. 13) также переводим в бинарный вид (рис. 16).

Имеются 4 маски и исходник по полученным данным. Позиции верхних левых углов:
маска 00 – ячейка (4, 4);
маска 01 – ячейка (4, 20);
маска 10 – ячейка (20, 4);
маска 11 – ячейка (20, 20);
исходные данные – ячейка (4, 36).
Добавляем четыре заготовки для будущих маскированных вариантов (рис. 17). Позиции верхних левых углов заготовок (4, 52), (4, 68), (20, 52) и (20, 68).

Пример полученного результата представлен на рисунке 18.

В ячейку (5, 61) добавляем следующую функцию:
=БИТ.ИСКЛИЛИ(RC[-48];RC[-16])
Если все сделано корректно, то в ячейке должна появиться цифра один (1). Дальше за нижний правый угол выделенной ячейки (магический квадрат MS Excel) заполняем все остальные ячейки матрицы (00).
В ячейку (5, 77) добавляем следующую функцию:
=БИТ.ИСКЛИЛИ(RC[-48];RC[-32])
Если все сделано корректно, то в ячейке должна появиться цифра один (1). Дальше за нижний правый угол выделенной ячейки (магический квадрат MS Excel) заполняем все остальные ячейки матрицы (01).
В ячейку (21, 61) добавляем следующую функцию:
=БИТ.ИСКЛИЛИ(RC[-48];R[-16]C[-16])
Если все сделано корректно, то в ячейке должна появиться цифра один (1). Дальше за нижний правый угол выделенной ячейки (магический квадрат MS Excel) заполняем все остальные ячейки матрицы (10).
В ячейку (21, 77) добавляем следующую функцию:
=БИТ.ИСКЛИЛИ(RC[-48];R[-16]C[-32])
Если все сделано корректно, то в ячейке должна появиться цифра один (0). Дальше за нижний правый угол выделенной ячейки (магический квадрат MS Excel) заполняем все остальные ячейки матрицы (11).
Пример результата маскирования представлен на рисунке 19.

Следующий этап – оценка символов Micro QR Code (п. 7.8.3.2 ГОСТ). После выполнения операции маскирования данных в области кодирования символа с каждым шаблоном маски данных оценивают результат, подсчитывая множество темных модулей в каждой из двух границ, которые не содержат шаблоны синхронизации. Чем меньше число темных модулей, тем менее приемлемым является результат. В таких символах рекомендуется иметь больше темных модулей на границе, чтобы более эффективно отличать свободную зону от области кодирования.
Для каждого шаблона маски данных подсчитывают число темных модулей в правой и нижней границах символа (исключая последний модуль шаблона синхронизации). Оценку результата подсчета производят следующим образом:
если SUM1 <= SUM2;
то оценка = SUM1 x 16 + SUM2;
если SUM1 > SUM2;
то оценка = SUM1 + SUM2 x 16;
где SUM1 – число темных модулей на правой границе;
SUM2 – число темных модулей на нижней границе.

Реализуем данную схему на Листе. Пример полученного результата представлен на рисунке 21.

Заполняем ячейки определения количества единиц (1) в правом столбике и нижней строчки каждой матрицы:
Ячейка | Функция |
(4, 87) | =СЧЁТЕСЛИ(R[1]C[-23]:R[12]C[-23];1) |
(4, 88) | =СЧЁТЕСЛИ(R[12]C[-35]:R[12]C[-24];1) |
(5, 87) | =СЧЁТЕСЛИ(RC[-7]:R[11]C[-7];1) |
(5, 88) | =СЧЁТЕСЛИ(R[11]C[-19]:R[11]C[-8];1) |
(6, 87) | =СЧЁТЕСЛИ(R[15]C[-23]:R[26]C[-23];1) |
(6, 88) | =СЧЁТЕСЛИ(R[26]C[-35]:R[26]C[-24];1) |
(7, 87) | =СЧЁТЕСЛИ(R[14]C[-7]:R[25]C[-7];1) |
(7, 88) | =СЧЁТЕСЛИ(R[25]C[-19]:R[25]C[-8];1) |
Заполняем ячейки определения критерия оценки для каждой матрицы:
Ячейка | Функция |
(4, 89)-(4, 90) | =ЕСЛИ(RC[-1]<RC[-2];RC[-1]*16+RC[-2];RC[-2]*16+RC[-1]) |
(5, 89)-(5, 90) | =ЕСЛИ(RC[-1]<RC[-2];RC[-1]*16+RC[-2];RC[-2]*16+RC[-1]) |
(6, 89)-(6, 90) | =ЕСЛИ(RC[-1]<RC[-2];RC[-1]*16+RC[-2];RC[-2]*16+RC[-1]) |
(7, 89)-(7, 90) | =ЕСЛИ(RC[-1]<RC[-2];RC[-1]*16+RC[-2];RC[-2]*16+RC[-1]) |
Выбирают шаблон маски, имеющий наибольший результат. Находим максимум из полученных вариантов. В ячейку (8,89)-(8,90) добавляем функцию:
=МАКС(R[-4]C:R[-1]C[1])
Проверяем полученный результат с примером на рисунке 21. В результате должно получиться число 104. Т.е. для данного символа рекомендуется использовать шаблон маски данных с обозначением 01 без вариативности, что наблюдалось в L режиме по ГОСТ (табл. 10). Применяем выбранный шаблон маски данных к области кодирования в матрице согласно п. 7.8 ГОСТ.
Этап 5. Подготовка информации о формате
В качестве исходных данных используются два показателя:
для символа версии M2-М номер равен 2, что в двоичном виде данных – 010 по таблице 13 ГОСТ (табл. 7);
полученный на 4 этапе шаблон маски – 01.
Таблица 7 – Номер символа для Micro QR Code
Номер символа | Версия | Уровень исправления ошибок | Двоичный индикатор |
0 | М1 | Только обнаружение | 000 |
1 | М2 | L | 001 |
2 | М2 | М | 010 |
3 | М3 | L | 011 |
4 | М3 | М | 100 |
5 | М4 | L | 101 |
6 | М4 | М | 110 |
7 | М4 | Q | 111 |
В результате получают биты данных в информации о формате 010 01:
01001
По таблице С.1 ГОСТ (табл. 8) находим соответствующую битовые последовательности информации о формате. Для данного примера – 110001010100100.
Hidden text
Таблица 8 – Надлежащие битовые последовательности информации о формате
Последовательность до маскирования | Последовательность после маскирования (символы Micro QR Code) | ||
Биты данных | Биты исправления ошибок | Двоичная | Шестнадцатеричная |
00000 | 0000000000 | 100010001000101 | 4445 |
00001 | 0100110111 | 100000101110010 | 4172 |
00010 | 1001101110 | 100111000101011 | 4Е2В |
00011 | 1101011001 | 100101100011100 | 4В1С |
00100 | 0111101011 | 101010110101110 | 55АЕ |
00101 | 0011011100 | 101000010011001 | 5099 |
00110 | 1110000101 | 101111111000000 | 5FC0 |
00111 | 1010110010 | 101101011110111 | 5AF7 |
01000 | 1111010110 | 110011110010011 | 6793 |
01001 | 1011100001 | 110001010100100 | 62А4 |
01010 | 0110111000 | 110110111111101 | 6DFD |
01011 | 0010001111 | 110100011001010 | 68СА |
01100 | 1000111101 | 111011001111000 | 7678 |
01101 | 1100001010 | 111001101001111 | 734F |
01110 | 0001010011 | 111110000010110 | 7С16 |
01111 | 0101100100 | 111100100100001 | 7921 |
10000 | 1010011011 | 000011011011110 | 06DE |
10001 | 1110101100 | 000001111101001 | 03Е9 |
10010 | 0011110101 | 000110010110000 | 0CB0 |
10011 | 0111000010 | 000100110000111 | 0987 |
10100 | 1101110000 | 001011100110101 | 1735 |
10101 | 1001000111 | 001001000000010 | 1202 |
10110 | 0100011110 | 001110101011011 | 1D5B |
10111 | 0000101001 | 001100001101100 | 186С |
11000 | 0101001101 | 010010100001000 | 2508 |
11001 | 0001111010 | 010000000111111 | 203F |
11010 | 1100100011 | 010111101100110 | 2F66 |
11011 | 1000010100 | 010101001010001 | 2А51 |
11100 | 0010100110 | 011010011100011 | 34E3 |
11101 | 0110010001 | 011000111010100 | 31D4 |
11110 | 1011001000 | 011111010001101 | 3E8D |
11111 | 1111111111 | 011101110111010 | ЗВВА |
Этап 6. Заключительное формирование символа
Добавляют модули информации о формате в позиции, зарезервированные на этапе 3, с 14 бита по 0 бит (рис. 22):
14 | 13 | 12 | 11 | 10 | 9 | 8 | 7 | 6 | 5 | 4 | 3 | 2 | 1 | 0 |
1 | 1 | 0 | 0 | 0 | 1 | 0 | 1 | 0 | 1 | 0 | 0 | 1 | 0 | 0 |

В результате получаем завершенный символ, приведенный на рис. 23.

Можно проверить полученный результат на любом онлайн сканере в сети Интернет. Выделяем в MS Excel полученный код и копируем через буфер обмена в MS Word как рисунок. В MS Word сохраняем полученный рисунок как внешний графический файл в формате .png. Загружаем произвольный онлайн сканер (например) и проверяем полученный Micro QR Code.