В минувшем году все только и говорили об ИИ и о том, как он может всё за вас сделать.
Мне нравится, когда кто-то или что-то работает за меня. Поэтому решил: попрошу-ка ChatGPT написать за меня новогодний пост:
"Эй, ChatGPT. А ты можешь реализовать большую языковую модель на SQL?"
"Нет, SQL не подходит для реализации больших языковых моделей. Язык SQL предназначен для выполнения запросов к данным, хранящимся в РСУБД и для управления этими запросами. Для реализации большой языковой модели требуются сложные алгоритмы, обширные датасеты, а зачастую – и фреймворки для глубокого обучения. SQL всеми этими возможностями не обладает."
Что ж, лишний раз убеждаешься, что, если хочешь что-то сделать хорошо – сделай это сам.
Давайте же воодушевимся этим оптимистическим планом и реализуем большую языковую модель на языке SQL.
Теория
Готовя этот пост, я вдохновлялся чудесной статьёй GPT in 60 Lines of NumPy, которую написал Джей Моди. В этой статье объяснено внутреннее устройство модели GPT, причём, это сделано гораздо лучше, чем могло бы получиться у меня. Поэтому для порядка вкратце напомню контекст.
Что представляет собой генеративная большая языковая модель с технической точки зрения?
Генеративная LLM – это функция. Она принимает на ввод текстовую последовательность символов (в терминологии ИИ она называется «промпт») и возвращает массив строк и чисел. Вот какова сигнатура этой функции:
llm(prompt: str) -> list[tuple[str, float]]
Это детерминированная функция. У неё под капотом выполняется серьёзная математика, но вся эта математика жёстко вшита в систему. Если вы будете многократно сообщать этой функции один и тот же ввод, то всякий раз будете получать от неё один и тот же вывод.
Тем, кому доводилось пользоваться ChatGPT и подобными продуктами, это может показаться удивительным, ведь система может давать разные ответы на один и тот же вопрос. Да, всё верно. Чуть ниже объясню, как это устроено.
Что за значения возвращает эта функция?
Нечто подобное:
llm("I wish you a happy New") 0 (' Year', 0.967553) 1 (' Years', 0.018199688) 2 (' year', 0.003573329) 3 (' York', 0.003114716) 4 (' New', 0.0009022804) … 50252 (' carbohyd', 2.3950911e-15) 50253 (' volunte', 2.2590102e-15) 50254 ('pmwiki', 1.369229e-15) 50255 (' proport', 1.1198108e-15) 50256 (' cumbers', 7.568147e-17)
Она возвращает массив кортежей. Каждый кортеж состоит из слова (скорее, строки) и числа. Число — это вероятность, с которой данное слово может оказаться промпте на следующей позиции. Модель «думает», что за фразой «I wish you a happy New…» («Поздравляю тебя с Новым…») с вероятностью 96,7% последует строка «Year» (…годом) – и так далее.
Слово «думает» выше поставлено в кавычках, так как, естественно, модель ни о чём не думает. Она механически возвращает массивы слов и чисел в соответствии с некоторой жёстко прописанной внутренней логикой.
Если эта система такая топорная и детерминированная, как же ей удаётся генерировать разные тексты?
Большие языковые модели используются в текстовых приложениях (чатботы, генераторы контента, кодинг-ассистенты, т.д.). Эти приложения раз за разом вызывают модель и выбирают подсказанное ею слово (с некоторой степенью произвольности). Последнее предложенное слово добавляется к промпту, и модель вызывается снова. Этот цикл продолжается до тех пор, пока не будет сгенерировано достаточное количество слов.
Накопленная таким образом последовательность слов выглядит как текст на естественном языке, с полноценной грамматикой, синтаксисом и даже мнимыми признаками интеллекта и логики. В данном отношении языковые модели подобны марковским цепям, работающим по такому же принципу.
На внутреннем уровне большая языковая модель устроена так, что каждое последующее предлагаемое слово естественным образом продолжало промпт, с учётом имеющейся грамматики, семантики и тональности. Оснастить функцию такой логикой стало возможно благодаря целой серии научных прорывов (и каторжной работе программистов). Удалось разработать целое семейство алгоритмов под названием GPT или «генеративные предобученные трансформеры».
Что такое "генеративный предобученный трансформер"
«Генеративный» означает, что алгоритм генерирует текст (рекурсивно достраивая продолжения к промпту как было показано выше).
«Трансформер» означает, что алгоритм использует конкретный тип нейронной сети. Сеть-трансформер была разработана компанией Google и описана в этой статье.
Термин «предобученный» требует небольшого исторического экскурса. Изначально считалось, что способность модели достраивать текст – это всего лишь предпосылка для получения более глубоких логических выводов в рамках специализированных задач (нужно улавливать логическую связь между фразами), классификации (например, угадать, сколько звёзд у отеля, проанализировав отзывы постояльцев), машинного перевода и т.д. Считалось, что две эти части алгоритма требуется обучать отдельно, и языковая часть позиционировалась как предобучение, подготовка к последующему обучению решать реальную задачу.
Как сформулировано в исходной статье по GPT:
Продемонстрировано, что возможно добиться больших успехов при решении таких задач путём генеративного предобучения языковой модели на разнородном корпусе неразмеченного текста с последующей тонкой настройкой различных параметров для различных слоёв сети (discriminative fine-tuning) в контексте каждой конкретной задачи.
Такие представления сохранялись до тех пор, пока не стало понятно, что для достаточно большой модели второй шаг зачастую излишен. Модель-трансформер, обученная исключительно генерации текстов, оказалась в состоянии без дополнительного обучения следовать человеческим инструкциям, содержащимся в этих текстах. Таким образом, не требовалось никакой дополнительной тонкой настройки.
Итак, с этими вопросами мы разобрались. Теперь давайте сосредоточимся на реализации.
Генерация
Вот что происходит, если мы пытаемся сгенерировать текст на основе промпта при помощи GPT2:
def generate(prompt: str) -> str: # Преобразует строку в список токенов. tokens = tokenize(prompt) # tokenize(prompt: str) -> list[int] while True: # Выполняет алгоритм. # Возвращает вероятностные значения для токенов: список из 50257 чисел с плавающей точкой, в сумме дающих 1. candidates = gpt2(tokens) # gpt2(tokens: list[int]) -> list[float] # Выбирает следующий токен из списка предложенных next_token = select_next_token(candidates) # select_next_token(candidates: list[float]) -> int # Прикрепляет его к списку токенов tokens.append(next_token) # Решаем, хотим ли мы прекратить генерацию. # Здесь может быть счётчик токенов, задержка, стоп-слово или что-то ещё. if should_stop_generating(): break # Преобразует список токенов в строку completion = detokenize(tokens) # detokenize(tokens: list[int]) -> str return completion
Давайте реализуем все эти элементы один за другим на языке SQL.
Токенизатор
Прежде, чем текст можно будет скормить нейронке, его требуется преобразовать в список чисел. Конечно, нас это не удивляет: именно такие задачи решаются при помощи текстовых кодировок вроде Unicode. Но обычный Unicode не слишком хорошо работает с нейронными сетями.
В сущности, нейронные сети построены на обширном перемножении матриц, и вся прогностическая сила нейронных сетей заключена в коэффициентах этих матриц. Некоторые из таких матриц содержат по строке на каждое из возможных значений в «алфавите», в других предусмотрено по строке на «символ».
В этом контексте смысл терминов «алфавит» и «символ» требуется пояснить. В Unicode длина «алфавита» составляет 149186 символов (именно столько отдельных точек Unicode существует на момент подготовки этой статьи), а в качестве «символа» может выступать, например: ﷽ (да, это одиночная точка Unicode, номер 65021, она соответствует целой фразе на арабском языке, особенно важной для мусульман). Отмечу, что эту фразу можно было бы записать и обычной арабской вязью. Таким образом, одному тексту может соответствовать несколько вариантов кодировки.
Давайте разберём эту ситуацию на примере слова "PostgreSQL". Если бы мы попытались закодировать её (преобразовать в массив чисел) при помощи Unicode, то у нас получилось бы 10 чисел, которые могли бы находиться в диапазоне от 1 до 149186. Таким образом, в нашей нейронной сети требовалось бы хранить матрицу из 149186 строк и совершить ряд вычислений над 10 строками из этой матрицы. Некоторые из этих строк (соответствующие буквам латиницы) использовались бы особенно часто, и в них было бы заключено много информации. Другие символы, например, смайлик какашки и таинственные символы из мёртвых языков едва ли вообще хоть раз использовались, но и на их хранение требуется место.
Естественно, мы хотим, чтобы оба эти числа, и длина «алфавита», и количество «символов» оставались как можно меньше. В идеале «символы» нашего алфавита должны быть распределены равномерно, а ещё мы по-прежнему хотим, чтобы наша кодировка не уступала по мощности Unicode.
Интуитивно понятно, что это можно сделать, присвоив уникальные номера тем последовательностям слов, которые часто встречаются в обрабатываемых нами текстах. В Unicode вышеупомянутая религиозная арабская фраза может быть закодирована либо как один кодовый символ, либо буква за буквой. Поскольку мы выкатываем нашу собственную кодировку, точно так же мы можем поступать с теми словами и фразами, которые важны в рамках нашей модели (например, они часто встречаются в текстах).
Например, можно было бы выделить конкретные числа для строк "Post", "greSQL" и "ing". Таким образом, оба сло��а "PostgreSQL" и "Posting" в нашем представлении будут иметь длину по 2. Конечно же, мы стремимся закреплять отдельные кодовые символы для более конкретных последовательностей и отдельных байт. Даже натыкаясь на тарабарщину или на иноязычный текст, такую информацию всё равно удастся закодировать, хотя, на это и потребуется больше времени.
В GPT2 используется вариант алгоритма под названием кодирование диадами (Byte Pair Encoding), предназначенный специально для этой цели. Токенизатор GPT2 использует словарь из 50257 кодовых точек (в терминологии ИИ — «токенов»), которые соответствуют различным последовательностям байт в UTF-8 (плюс отдельный токен, означающий «конец текста»).
Этот словарь мы собрали путём статистического анализа, выполненного таким образом:
Начинаем с простой кодировки из 256 токенов: по токену за байт.
Берём большой корпус текстов (предпочтительно именно тот, на котором будет обучаться модель).
Кодируем его.
Вычисляем, какая пара токенов встречается чаще всего. Пусть это будет 0x20 0x74 (пробел, за которым следует строчная "t").
Присваиваем следующее доступное значение (257) этой паре байт.
Повторяем шаги 3-5, теперь обращая внимание на последовательности байт. Если последовательность байт можно закодировать сложным токеном, то используем сложный токен. При явных неоднозначностях (например, "abc" может в одном случае быть закодировано как "a" + "bc" или как "ab" + "c"), то пользуйтесь той, номер которой меньше (это означает, что она была добавлена раньше и, следовательно, встречается чаще). Это нужно делать рекурсивно, пока все последовательности, которые можно сложить в один токен, будут сложены в один токен.
Выполним такое «складывание» 50000 раз подряд.
Число 50000 выбрано разработчиками более или менее произвольно. В других моделях количество токенов также держится в подобном диапазоне (от 30k до 100k).
На каждой итерации данного алгоритма в словарь будет добавляться новый токен, получаемый конкатенацией двух предыдущих. В конечном итоге получим 50256 токенов. Добавляем токен с фиксированным номером, означающий «конец текста» - и всё готово.
В версии алгоритма BTE для GPT2 есть ещё один уровень кодировки: в словаре токенов эти токены отображаются на строки, а не на массивы байт. Отображение с байт на строковые символы определяется в этой функции. Тот словарь, который она производит, находится в таблице encoder.
Рассмотрим, как реализовать токенизатор на SQL.
Данный токенизатор – неотъемлемая часть GPT2, и словарь токенов можно скачать с сайта OpenAI, равно как и оставшуюся часть модели. Нам понадобится импортировать её в таблицу tokenizer. В самом конце этого поста вы найдёте ссылку на репозиторий с кодом. Этот код автоматизирует заполнение таблиц базы данных, необходимых для работы с моделью.
В рамках рекурсивного подхода CTE разбиваем слово на токены (начиная с единичных байт) и объединяем наилучшие смежные пары, пока больше материала для объединения не останется. Само объединение происходит по принципу вложенного рекурсивного CTE.
Для примера я выбрал слово «Mississippilessly». Каждая запись в наборе результатов соответствует наилучшей найденной к данному моменту паре, которую можно «сложить», а также прогресс в обработке запроса.
WITH RECURSIVE bpe AS ( SELECT (n + 1)::BIGINT AS position, character, TRUE AS continue, 1 AS step, NULL::INT AS token, NULL::TEXT AS combined FROM CONVERT_TO('Mississippilessly', 'UTF-8') AS bytes CROSS JOIN LATERAL GENERATE_SERIES(0, LENGTH(bytes) - 1) AS n JOIN encoder ON byte = GET_BYTE(bytes, n) UNION ALL ( WITH RECURSIVE base AS ( SELECT * FROM bpe WHERE continue ), bn AS ( SELECT ROW_NUMBER() OVER (ORDER BY position) AS position, continue, character, character || LEAD(character) OVER (ORDER BY position) AS cluster FROM base ), top_rank AS ( SELECT tokenizer.* FROM bn CROSS JOIN LATERAL ( SELECT * FROM tokenizer WHERE tokenizer.cluster = bn.cluster LIMIT 1 ) tokenizer ORDER BY token LIMIT 1 ), breaks AS ( SELECT 0::BIGINT AS position, 1 AS length UNION ALL SELECT bn.position, CASE WHEN token IS NULL THEN 1 ELSE 2 END FROM breaks JOIN bn ON bn.position = breaks.position + length LEFT JOIN top_rank USING (cluster) ) SELECT position, character, token IS NOT NULL, (SELECT step + 1 FROM base LIMIT 1), token, top_rank.cluster FROM breaks LEFT JOIN top_rank ON 1 = 1 CROSS JOIN LATERAL ( SELECT STRING_AGG(character, '' ORDER BY position) AS character FROM bn WHERE bn.position >= breaks.position AND bn.position < breaks.position + length ) bn WHERE position > 0 ) ) SELECT step, MAX(token) AS token, MAX(combined) AS combined, ARRAY_AGG(character ORDER BY position) FROM bpe WHERE continue GROUP BY step ORDER BY step
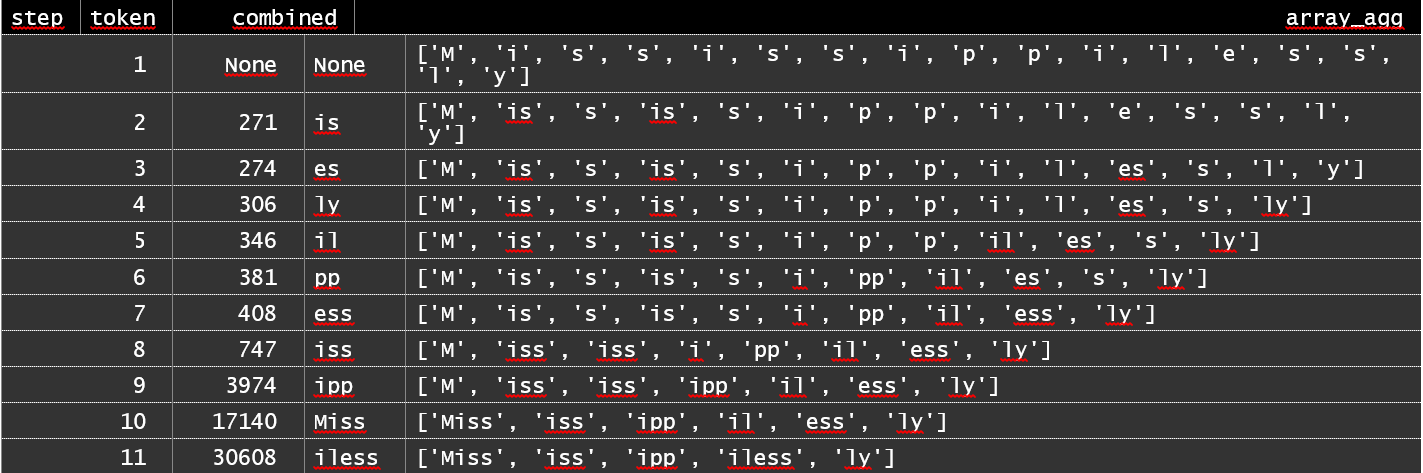
На каждом шаге алгоритм BPE находит пару токенов, наиболее подходящую для слияния, и объединяет их (здесь в выводе вы видите такую слитую пару и ее ранг). При помощи такой процедуры размер пространства токенов можно сократить с 150k, присущих Unicode, до 50k, а количество токенов в данном конкретном слове с 17 до 5. В обоих случаях это отличное улучшение.
Когда приходится работать с множеством слов, токенизатор сначала разбивает текст на отдельные слова при помощи этого регулярного выражения и объединяет токены в каждом слове отдельно. К сожалению, при работе с PostgreSQL свойства символов Unicode не поддерживаются на уровне регулярных выражений, поэтому мне пришлось немного отладить систему (возможно, в процессе я угробил нормальную поддержку Unicode). Вот как результат выглядит в SQL:
WITH input AS ( SELECT 'PostgreSQL is great' AS prompt ), clusters AS ( SELECT part_position, bpe.* FROM input CROSS JOIN LATERAL REGEXP_MATCHES(prompt, '''s|''t|''re|''ve|''m|''ll|''d| ?\w+| ?\d+| ?[^\s\w\d]+|\s+(?!\S)|\s+', 'g') WITH ORDINALITY AS rm (part, part_position) CROSS JOIN LATERAL ( WITH RECURSIVE bpe AS ( SELECT (n + 1)::BIGINT AS position, character, TRUE AS continue FROM CONVERT_TO(part[1], 'UTF-8') AS bytes CROSS JOIN LATERAL GENERATE_SERIES(0, LENGTH(bytes) - 1) AS n JOIN encoder ON byte = GET_BYTE(bytes, n) UNION ALL ( WITH RECURSIVE base AS ( SELECT * FROM bpe WHERE continue ), bn AS ( SELECT ROW_NUMBER() OVER (ORDER BY position) AS position, continue, character, character || LEAD(character) OVER (ORDER BY position) AS cluster FROM base ), top_rank AS ( SELECT tokenizer.* FROM bn CROSS JOIN LATERAL ( SELECT * FROM tokenizer WHERE tokenizer.cluster = bn.cluster LIMIT 1 ) tokenizer ORDER BY token LIMIT 1 ), breaks AS ( SELECT 0::BIGINT AS position, 1 AS length UNION ALL SELECT bn.position, CASE WHEN token IS NULL THEN 1 ELSE 2 END FROM breaks JOIN bn ON bn.position = breaks.position + length LEFT JOIN top_rank USING (cluster) ) SELECT position, character, token IS NOT NULL FROM breaks LEFT JOIN top_rank ON 1 = 1 CROSS JOIN LATERAL ( SELECT STRING_AGG(character, '' ORDER BY position) AS character FROM bn WHERE bn.position >= breaks.position AND bn.position < breaks.position + length ) bn WHERE position > 0 ) ) SELECT position, character AS cluster FROM bpe WHERE NOT continue ) bpe ), tokens AS ( SELECT token, cluster FROM clusters JOIN tokenizer USING (cluster) ) SELECT * FROM tokens

Странный символ Ġ соответствует пробелу.
Этот запрос токенизирует промпт и преобразует его в массив чисел. Вот промпт и готов к долгому пути сквозь слои модели.
Векторные представления
Токены - это представления единиц естественного языка (в целом, примерно 0,75 слова на токен), поэтому любая модель, претендующая на успешное автозавершение текстов, должна каким-то образом кодировать отношения между этими единицами. Даже в изоляции части речи обладают наборами ортогональных свойств.
Возьмём, к примеру, слово «subpoena» (повестка) – оказывается, в токенизаторе GPT2 на него отведён целый токен. С точки зрения английского языка – это существительное? Да, бесспорно. А глагол? Да, и глаголом может быть. А прилагательным? Уже не очень, но, в принципе, контекст придумать можно. Это канцелярит? Чёрт возьми, ещё какой. И так далее.
Все эти свойства ортогональны, то есть, не зависят друг от друга. Слово может быть официозным существительным, но не глаголом и не прилагательным. В английском возможны любые сочетания этих признаков.
Сущности с ортогональными свойствами лучше всего кодируются в виде векторных представлений. Пусть у нас будет не единственное свойство (например, номер), а много. При желании мы можем крутить ими как захотим. Например, фраза «В судебном решении, которое процитировал адвокат, фигурирует…» с высокой вероятностью продолжается каким-то существительным, которое, не менее вероятно, стилистически относится к канцеляриту. Нас совершенно не интересует, есть ли у этого слова маргинальная семантика «глагол», либо «прилагательное», либо «цветок».
В математике отображение сравнительно узких значений на более широкие пространства (например, ID токенов на векторы) называется векторным представлением. Именно этим мы здесь и занимаемся.
Как решить, какие именно свойства окажутся представлены в этих векторах? А мы не будем. Мы просто предоставим достаточно векторного пространства для каждого токена и понадеемся, что модель на этапе обучения получит достаточно информации, чтобы заполнить все эти измерения осмысленным содержимым. В GPT2 под векторы отводится 768 измерений. Заранее (и, на самом деле, даже в ретроспективе) не известно, какое свойство слова будет закодировано, например, в измерении 247. Определённо, что-то закодировано там будет, но что именно – сказать сложно.
Какие свойства каждого из токенов мы внедрим в векторное пространство? Любые, которые помогут нам спрогнозировать, каков будет следующий токен.
ID токена? Естественно. Разные токены означают разные вещи.
Позиция токена в тексте? Да, пожалуйста. «Сине-фиолетовый» и «фиолетово-синий» — не одно и то же.
Взаимные отношения токенов? Естественно! Это, пожалуй, наиважнейшая часть задачи, и блок внимания (Attention) в архитектуре трансформе��а как раз впервые позволил решить эту часть задачи правильно.
Токены и позиции легко поддаются векторному представлению. Допустим, есть фраза «PostgreSQL is great», о которой заранее известно, что она отображается на четыре токена: [6307, 47701, 318, 1049].
Среди прочих параметров GPT2 есть две матрицы, называющиеся WTE (векторное представление лексических токенов) и WPE (векторное представление позиций слов). Как понятно из названия, в первом хранятся векторные представления токенов, а во втором – векторные представления их позиций. Конкретные значения, которыми окажутся заполнены эти представления, набираются в результате обучения модели, в данном случае GPT2. Насколько известно, в таблицах баз данных wte и wpe есть константы. Размер
WTE равен 50257×768, а размер WPE равен 1024×768. Второе означает, что в GPT2 можно использовать промпт, состоящий не более чем из 1024 токенов. Если записать в промпт больше токенов, мы просто не сможем вытянуть для токенов сверх 1024 их позиционные представления. Это архитектурный аспект (в терминологии ИИ – «гиперпараметр») модели, устанавливаемый на этапе её проектирования, и обучением его изменить невозможно. Когда говорят о «контекстном окне» большой языковой модели, имеют в виду именно это число.
Токен 6307 стоит у нас на месте 0, токен 47701 на месте 1, токен 318 на месте 2, а токен 1049 на месте 3. Для каждого из этих токенов и их позиций у нас по два вектора: один из WTE и один из WPE. Их требуется сложить. В результате получатся четыре вектора, которые послужат вводом для следующей части алгоритма: так работает нейронная сеть прямого распространения, в которой действует механизм внимания.
Для работы с SQL мы воспользуемся pgvector, это расширение PostgreSQL.
Небольшая оговорка: код для этого поста я пишу на обычном SQL, иногда вставляю чистые SQL-функции в качестве вспомогательных элементов. В рамках этого поста осуществить такое не составит труда, равно как определить векторные операции над массивами. Это делается за счёт небольшого снижения производительности (и уже было реализовано в версии 1 и работало, пусть и медленно). С распространением ИИ и ростом влияния векторных баз данных pgvector или эквивалентный механизм определённо укоренится в ядре PostgreSQL в течение двух-трёх релизов. Я просто решил оседлать волну, которая принесёт меня в будущее.
Вот как это делается в SQL:
WITH embeddings AS ( SELECT place, values FROM UNNEST(ARRAY[6307, 47701, 318, 1049]) WITH ORDINALITY AS tokens (token, ordinality) CROSS JOIN LATERAL ( SELECT ordinality - 1 AS place ) o CROSS JOIN LATERAL ( SELECT wte.values + wpe.values AS values FROM wte CROSS JOIN wpe WHERE wte.token = tokens.token AND wpe.place = o.place ) embedding ) SELECT place, (values::REAL[])[0:5] FROM embeddings

(Чтобы вывод был короче, в этом запросе показаны только первые 5 измерений для каждого вектора).
Внимание
Та часть трансформерной архитектуры, благодаря которой она действительно феерит, называется «механизм внутреннего внимания» (self-attention). Он был впервые описан в 2017 году в статье «Attention is all you need» под авторством Васмани и др. Пожалуй, это наиизвестнейшая статья об искусственном интеллекте, и с тех пор её название превратилось в болванку (клише для именования других статей).
Итак, вероятно, к настоящему моменту у нас уже есть несколько векторов, в которых закодированы определённые синтаксические и семантические свойства слов, содержащихся в нашем промпте. Нам каким-то образом нужно донести эти свойства до последнего вектора. Сейчас будет небольшой спойлер: именно в последнем векторе будет храниться представление того слова, которым продолжится фраза.
Во фразе вида a «I looked at the violet and saw that it was not the usual …» (я взглянул на лиловое пятно и заметил, что это не обычный…), на месте многоточия должно быть что-то, увиденное вами (об этом свидетельствует слово «saw»), обладающее свойством «лиловости» и при этом «необычное» (сочетаем токены «не» и «обычный», тем самым меняя знак измерения «обычность» на противоположный). Можно привести такую реалистичную аналогию: человек читает книгу на иностранном языке, о котором имеет некоторое представление, но свободно им не владеет. В таком случае человеку придётся аккуратно сплетать каждое слово со следующим, и, если он не обратит внимания на ключевую часть фразы, то всю фразу поймёт неправильно.
Чтобы обеспечить такой перенос значения от одного токена к другому, требуется разрешить векторам всех токенов влиять друг на друга. Так, возвращаясь к английскому: если мы хотим наполнить слово «it» конкретной семантикой, то какая часть семантики должна поступить от предыдущих векторов в промпте, а какая – остаться от самого слова «it»?
В данной модели эта задача решается при помощи 12 наборов матриц, именуемых Q (запрос), K (ключ) и V (значение). В каждой из них по 64 столбца. Их мы получаем из векторных представлений через 768×2304-мерное линейное преобразование c_attn, веса и смещения которого хранятся в таблицах c_attn_w и c_attn_b.
Результатом c_attn является матрица со n_token строк и 2304 столбцами (3×12×64). Она состоит из 12 Q-матриц, 12 K-матриц и 12 V-матриц, упорядоченных горизонтально именно в таком порядке.
Каждый набор, состоящий из Q, K и V, называется «головой». С их помощью выполняется шаг под названием «многоголовое условное внутреннее внимание», на котором вычисляется функция внимания.
Она вычисляется по этой формуле:
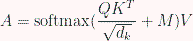
где softmax – это функция нормализации весов. Она определяется так:
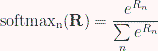
M - это матрица-константа, именуемая «условной маской». Она определяется так:
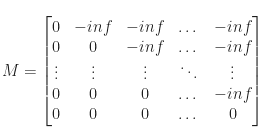
Функция Softmax обнуляет все отрицательные бесконечности.
Почему необходимо использовать маски?
В промпте из предыдущего примера было 4 токена, и модель первым делом вычисляла 4 векторных представления для 4 этих токенов. По мере дальнейшей работы модели над этими векторами будет выполнено много вычислений, но в основном они пойдут независимо и параллельно. Изменения в одном векторе не затронут другие векторы, как если бы иных векторов не существовало. Векторы влияют друг на друга только в пределах блока внутреннего внимания.
Как только модель справится с математикой, претенденты на роль следующего токена будут выбираться исключительно исходя из последнего векторного представления. Вся информация должна направляться именно к этому последнему вектору, а не прочь от него. Временные значения последнего вектора не должны влиять на временные значения предыдущих векторов, использовавшихся в ходе прямого распространения по данной модели.
Именно поэтому мы «маскируем» позднейшие векторы, чтобы они не влияли на более ранние через этот конкретный канал. В этом и заключается условность «многоголового условного внутреннего внимания».
Почему матрицы называются "запрос", "ключ" и "значение"?
Честно говоря, даже не уверен, что это хорошая аналогия. Но, тем не менее, попытаюсь объяснить, какова логика таких названий.
Как правило, в машинном обучении при вычислениях не должны использоваться циклы переменной длины или ветвление инструкций. Все задачи должны решаться компоновкой простых аналитических функций (сложение, умножение, возведение в степень, логарифмы и тригонометрия). Так обеспечивается обратное распространение для эффективной реализации которого требуются такие технологии, как автоматическое дифференцирование.
Математическая модель хранилища ключей и значений заключена в таком выражении:
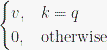
Но это не гладкая дифференцируемая функция, и с обратным распространением она работать не будет. Чтобы формула работала, необходимо получить гладкую функцию, которая была бы близка к v, когда k близка к q, и близка к 0 в иных случаях.
Для этой цели отлично подходит Гауссово распределение («колоколообразная кривая») "bell curve"), отмасштабированная к v с ожиданием k и достаточно небольшим стандартным отклонением:
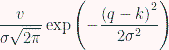
где σ - произвольный параметр, определяющий, насколько «остра» колоколообразная кривая.
Если взять в векторном пространстве с достаточно большим количеством измерений фиксированный вектор K и несколько векторов Q, которые случайным и равномерным образом отклоняются от K в каждом из измерений, то их скалярные произведения сложатся именно в колоколообразную кривую. Соответственно, в векторном пространстве «дифференцируемое хранилище ключей и значений» можно смоделировать при помощи выражения
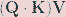
того самого, которым мы пользовались в нашей функции внимания.
Опять же, эта аналогия немного натянута. Лучше не слишком зацикливаться на концептуальной составляющей внимания, то есть, на потоке операций, хеш-таблицах и пр. Можете считать, что они просто вдохновили меня на описанный математический фокус, который я догадался протестировать – и на практике он оказался весьма хорош.
Проиллюстрирую этот шаг:
WITH embeddings AS ( SELECT place, values FROM UNNEST(ARRAY[6307, 47701, 318, 1049]) WITH ORDINALITY AS tokens (token, ordinality) CROSS JOIN LATERAL ( SELECT ordinality - 1 AS place ) o CROSS JOIN LATERAL ( SELECT wte.values + wpe.values AS values FROM wte CROSS JOIN wpe WHERE wte.token = tokens.token AND wpe.place = o.place ) embedding ), c_attn_w AS ( SELECT * FROM c_attn_w WHERE block = 0 ), c_attn_b AS ( SELECT * FROM c_attn_b WHERE block = 0 ), ln_1_g AS ( SELECT * FROM ln_1_g WHERE block = 0 ), ln_1_b AS ( SELECT * FROM ln_1_b WHERE block = 0 ), mha_norm AS ( SELECT place, mm.values + c_attn_b.values AS values FROM ( SELECT place, ARRAY_AGG(INNER_PRODUCT(c_attn_w.values, layer_norm.values) ORDER BY y)::VECTOR(2304) AS values FROM ( SELECT place, agg.values * ln_1_g.values + ln_1_b.values AS values FROM ( SELECT place, norm.values FROM embeddings CROSS JOIN LATERAL ( SELECT AVG(value) AS mean, VAR_POP(value) AS variance FROM UNNEST(values::REAL[]) value ) agg CROSS JOIN LATERAL ( SELECT ARRAY_AGG((value - mean) / SQRT(variance + 1E-5) ORDER BY ordinality)::VECTOR(768) AS values FROM UNNEST(values::REAL[]) WITH ORDINALITY AS n(value, ordinality) ) norm ) agg CROSS JOIN ln_1_b CROSS JOIN ln_1_g ) layer_norm CROSS JOIN c_attn_w GROUP BY place ) mm CROSS JOIN c_attn_b ), head AS ( SELECT place, (values::REAL[])[1:64]::VECTOR(64) AS q, (values::REAL[])[1 + 768:64 + 768]::VECTOR(64) AS k, (values::REAL[])[1 + 1536:64 + 1536]::VECTOR(64) AS v FROM mha_norm ), sm_input AS ( SELECT h1.place AS x, h2.place AS y, INNER_PRODUCT(h1.q, h2.k) / 8 + CASE WHEN h2.place > h1.place THEN -1E10 ELSE 0 END AS value FROM head h1 CROSS JOIN head h2 ), sm_diff AS ( SELECT x, y, value - MAX(value) OVER (PARTITION BY x) AS diff FROM sm_input ), sm_exp AS ( SELECT x, y, CASE WHEN diff < -745.13 THEN 0 ELSE EXP(diff) END AS e FROM sm_diff ), softmax AS ( SELECT x, y AS place, e / SUM(e) OVER (PARTITION BY x) AS value FROM sm_exp ), attention AS ( SELECT place, (ARRAY_AGG(value ORDER BY ordinality))[:3] AS values FROM ( SELECT x AS place, SUM(ARRAY_FILL(softmax.value, ARRAY[64])::VECTOR(64) * head.v) AS values FROM softmax JOIN head USING (place) GROUP BY x ) q CROSS JOIN LATERAL UNNEST(values::REAL[]) WITH ORDINALITY v (value, ordinality) GROUP BY place ) SELECT place, (SELECT STRING_AGG(TO_CHAR(n, 'S0.000'), ' ') || ' …' FROM UNNEST((q::REAL[])[:3]) AS n) AS q, (SELECT STRING_AGG(TO_CHAR(n, 'S0.000'), ' ') || ' …' FROM UNNEST((k::REAL[])[:3]) AS n) AS k, (SELECT STRING_AGG(TO_CHAR(n, 'S0.000'), ' ') || ' …' FROM UNNEST((v::REAL[])[:3]) AS n) AS v, matrix, (SELECT STRING_AGG(TO_CHAR(n, 'S0.000'), ' ') || ' …' FROM UNNEST((values::REAL[])[:3]) AS n) AS attention FROM head JOIN attention USING (place) JOIN ( SELECT x AS place, STRING_AGG(CASE WHEN value > 0 THEN TO_CHAR(value, '0.00') ELSE ' 0' END, ' ' ORDER BY place) AS matrix FROM softmax GROUP BY x ) softmax_grouped USING (place)

Вот что мы сделали:
Прежде, чем вычислять функцию внимания, мы нормализовали векторы при помощи линейного преобразования R’ = RГ1 + B1. Матрица Г1 и вектор B1называются, соответственно, «масштабирование» и «сдвиг». Это параметры, изученные моделью, которые хранятся в таблицах ln_1_g и ln_1_b
Мы показываем только первую голову первого слоя, используемого в этом алгоритме. После того, как умножим векторы на изученные коэффициенты из c_attn_w и c_attn_b («вес» и «смещение»), порежем полученные в результате 2304-мерные векторы. Возьмём 64-мерные векторы, начинающиеся в позициях 0, 768 и 1536. Они соответствуют векторам Q, K и V первой головы.
EXP в PostgreSQL плохо работает с очень малыми числами, и именно поэтому мы прибегаем к нулю, если EXP получает аргумент менее -745,13.
Для каждого вектора мы показываем только первые три элемента. Марицу внимания показываем полностью.
Итак, значение первого вектора копируется в вывод как есть (так мы поступаем с первым значением на каждом слое алгоритма). Это означает, что, когда модель уже обучена, результирующее векторное представление первого токена будет определяться только значением первого токена. В принципе, на этапе рекурсивного вывода, пока токены только добавляются в промпт, по сравнению с предыдущей итерацией изменится лишь самое последнее векторное представление в выводе. Именно поэтому применяется условная маска.
Заглянем немного вперёд: блок внимания – это единственное место во всём алгоритме, где токены могут влиять друг на друга на этапе прямого прохода. Поскольку на данном этапе мы не позволяем позднейшим токенам влиять на более раннее (и отключили такую возможность), все вычисления, проделанные над более ранними токенами, можно повторно использовать на разных итерациях прямого прохода по модели.
Напомню, модель при работе добавляет токены в промпт. Если исходный (токенизированный) промпт – это «Post greSQL Ġis Ġgreat», а следующий, например, будет «Post greSQL Ġis Ġgreat Ġfor», то все результаты вычислений, проделанных над первыми четырьмя токенами, можно будет повторно использовать и в новом промпте. Они никогда не изменятся, независимо от того, что ещё будет прикреплено к этому промпту.
В статье Джея Муди, которую я привёл для примера, этот аспект не задействуется (равно как и в моей статье – для простоты), но в оригинальной реализации GPT2 он задействован.
Закончив работу со всеми головами, получаем 12 матриц. Каждая из них будет по 64 столбца в ширину и по n_tokens строк в высоту. Чтобы вновь отобразить её на размерность векторных представлений (768), нам просто нужно составить эти матрицы горизонтально.
Последний этап обработки многоголового внимания связан с проецированием значений путём линейного преобразования в том же самом измерении. Соответствующие веса и смещения хранятся в таблицах c_proj_w и c_proj_b.
Ниже приведён полный код, описывающий реализацию многоголового внимания в первом слое:
WITH embeddings AS ( SELECT place, values FROM UNNEST(ARRAY[6307, 47701, 318, 1049]) WITH ORDINALITY AS tokens (token, ordinality) CROSS JOIN LATERAL ( SELECT ordinality - 1 AS place ) o CROSS JOIN LATERAL ( SELECT wte.values + wpe.values AS values FROM wte CROSS JOIN wpe WHERE wte.token = tokens.token AND wpe.place = o.place ) embedding ), c_proj_w AS ( SELECT * FROM c_proj_w WHERE block = 0 ), c_proj_b AS ( SELECT * FROM c_proj_b WHERE block = 0 ), mlp_c_fc_w AS ( SELECT * FROM mlp_c_fc_w WHERE block = 0 ), mlp_c_fc_b AS ( SELECT * FROM mlp_c_fc_b WHERE block = 0 ), mlp_c_proj_w AS ( SELECT * FROM mlp_c_proj_w WHERE block = 0 ), mlp_c_proj_b AS ( SELECT * FROM mlp_c_proj_b WHERE block = 0 ), c_attn_w AS ( SELECT * FROM c_attn_w WHERE block = 0 ), c_attn_b AS ( SELECT * FROM c_attn_b WHERE block = 0 ), ln_1_g AS ( SELECT * FROM ln_1_g WHERE block = 0 ), ln_1_b AS ( SELECT * FROM ln_1_b WHERE block = 0 ), mha_norm AS ( SELECT place, mm.values + c_attn_b.values AS values FROM ( SELECT place, ARRAY_AGG(INNER_PRODUCT(c_attn_w.values, layer_norm.values) ORDER BY y)::VECTOR(2304) AS values FROM ( SELECT place, agg.values * ln_1_g.values + ln_1_b.values AS values FROM ( SELECT place, norm.values FROM embeddings CROSS JOIN LATERAL ( SELECT AVG(value) AS mean, VAR_POP(value) AS variance FROM UNNEST(values::REAL[]) value ) agg CROSS JOIN LATERAL ( SELECT ARRAY_AGG((value - mean) / SQRT(variance + 1E-5) ORDER BY ordinality)::VECTOR(768) AS values FROM UNNEST(values::REAL[]) WITH ORDINALITY AS n(value, ordinality) ) norm ) agg CROSS JOIN ln_1_b CROSS JOIN ln_1_g ) layer_norm CROSS JOIN c_attn_w GROUP BY place ) mm CROSS JOIN c_attn_b ), heads AS ( SELECT place, head, (values::REAL[])[(head * 64 + 1):(head * 64 + 64)]::VECTOR(64) AS q, (values::REAL[])[(head * 64 + 1 + 768):(head * 64 + 64 + 768)]::VECTOR(64) AS k, (values::REAL[])[(head * 64 + 1 + 1536):(head * 64 + 64 + 1536)]::VECTOR(64) AS v FROM mha_norm CROSS JOIN GENERATE_SERIES(0, 11) head ), sm_input AS ( SELECT head, h1.place AS x, h2.place AS y, INNER_PRODUCT(h1.q, h2.k) / 8 + CASE WHEN h2.place > h1.place THEN -1E10 ELSE 0 END AS value FROM heads h1 JOIN heads h2 USING (head) ), sm_diff AS ( SELECT head, x, y, value - MAX(value) OVER (PARTITION BY head, x) AS diff FROM sm_input ), sm_exp AS ( SELECT head, x, y, CASE WHEN diff < -745.13 THEN 0 ELSE EXP(diff) END AS e FROM sm_diff ), softmax AS ( SELECT head, x, y AS place, e / SUM(e) OVER (PARTITION BY head, x) AS value FROM sm_exp ), attention AS ( SELECT place, ARRAY_AGG(value ORDER BY head * 64 + ordinality)::VECTOR(768) AS values FROM ( SELECT head, x AS place, SUM(ARRAY_FILL(softmax.value, ARRAY[64])::VECTOR(64) * heads.v) AS values FROM softmax JOIN heads USING (head, place) GROUP BY head, x ) q CROSS JOIN LATERAL UNNEST(values::REAL[]) WITH ORDINALITY v (value, ordinality) GROUP BY place ), mha AS ( SELECT place, w.values + c_proj_b.values AS values FROM ( SELECT attention.place, ARRAY_AGG(INNER_PRODUCT(attention.values, c_proj_w.values) ORDER BY c_proj_w.place)::VECTOR(768) AS values FROM attention CROSS JOIN c_proj_w GROUP BY attention.place ) w CROSS JOIN c_proj_b ) SELECT place, (SELECT STRING_AGG(TO_CHAR(n, 'S0.000'), ' ') || ' …' FROM UNNEST((values::REAL[])[:10]) AS n) AS q FROM mha

Прежде чем результаты многоголового внимания будут переданы на следующий шаг, к ним нужно добавить оригинальные входные данные. Этот фокус был описан ещё в исходной статье по трансформерам. Предполагается, что он должен помочь с затухающими и взрывными градиентами.
Это распространённая проблема при обучении: иногда градиенты параметров оказываются слишком малы или слишком велики. Если менять их при очередной итерации обучения, это также очень слабо влияет на функцию потерь (поэтому модель сходится очень медленно). Бывает и обратный эффект: даже минимальное изменение отбрасывает функцию потерь слишком далеко от локального минимума, тем самым обесценивая всю работу по обучению.
Прямое распространение
Именно в этом и заключается работа глубоких нейронных сетей. Большая часть параметров модели на самом деле используется именно на этом этапе.
Здесь мы имеем дело с многослойным перцептроном, у которого три слоя (768, 3072, 768), а в качестве функции активации используем линейную единицу гауссовской ошибки (GELU):
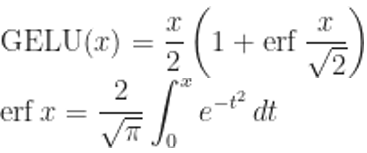
Как показывает практика, эта функция даёт очень хорошие результаты при работе с глубокими нейронными сетями. Её можно аналитически аппроксимировать вот так:
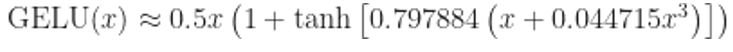
Изученные параметры линейного преобразования для связей в слое называются c_fc (768 → 3072) и c_proj (3072 → 768). Значения с первого слоя сначала нормализуются при помощи коэффициентов, содержащихся в изученном параметре ln_2. По завершении этапа прямого распространения его ввод вновь добавляется к выводу. Этот элемент также входит в самый первый вариант дизайна трансформеров. Весь этап прямого распространения выглядит так:
А вот как это делается на SQL:
WITH embeddings AS ( SELECT place, values FROM UNNEST(ARRAY[6307, 47701, 318, 1049]) WITH ORDINALITY AS tokens (token, ordinality) CROSS JOIN LATERAL ( SELECT ordinality - 1 AS place ) o CROSS JOIN LATERAL ( SELECT wte.values + wpe.values AS values FROM wte CROSS JOIN wpe WHERE wte.token = tokens.token AND wpe.place = o.place ) embedding ), c_proj_w AS ( SELECT * FROM c_proj_w WHERE block = 0 ), c_proj_b AS ( SELECT * FROM c_proj_b WHERE block = 0 ), mlp_c_fc_w AS ( SELECT * FROM mlp_c_fc_w WHERE block = 0 ), mlp_c_fc_b AS ( SELECT * FROM mlp_c_fc_b WHERE block = 0 ), mlp_c_proj_w AS ( SELECT * FROM mlp_c_proj_w WHERE block = 0 ), mlp_c_proj_b AS ( SELECT * FROM mlp_c_proj_b WHERE block = 0 ), c_attn_w AS ( SELECT * FROM c_attn_w WHERE block = 0 ), c_attn_b AS ( SELECT * FROM c_attn_b WHERE block = 0 ), ln_1_g AS ( SELECT * FROM ln_1_g WHERE block = 0 ), ln_1_b AS ( SELECT * FROM ln_1_b WHERE block = 0 ), ln_2_b AS ( SELECT * FROM ln_2_b WHERE block = 0 ), ln_2_g AS ( SELECT * FROM ln_2_g WHERE block = 0 ), mha_norm AS ( SELECT place, mm.values + c_attn_b.values AS values FROM ( SELECT place, ARRAY_AGG(INNER_PRODUCT(c_attn_w.values, layer_norm.values) ORDER BY y)::VECTOR(2304) AS values FROM ( SELECT place, agg.values * ln_1_g.values + ln_1_b.values AS values FROM ( SELECT place, norm.values FROM embeddings CROSS JOIN LATERAL ( SELECT AVG(value) AS mean, VAR_POP(value) AS variance FROM UNNEST(values::REAL[]) value ) agg CROSS JOIN LATERAL ( SELECT ARRAY_AGG((value - mean) / SQRT(variance + 1E-5) ORDER BY ordinality)::VECTOR(768) AS values FROM UNNEST(values::REAL[]) WITH ORDINALITY AS n(value, ordinality) ) norm ) agg CROSS JOIN ln_1_b CROSS JOIN ln_1_g ) layer_norm CROSS JOIN c_attn_w GROUP BY place ) mm CROSS JOIN c_attn_b ), heads AS ( SELECT place, head, (values::REAL[])[(head * 64 + 1):(head * 64 + 64)]::VECTOR(64) AS q, (values::REAL[])[(head * 64 + 1 + 768):(head * 64 + 64 + 768)]::VECTOR(64) AS k, (values::REAL[])[(head * 64 + 1 + 1536):(head * 64 + 64 + 1536)]::VECTOR(64) AS v FROM mha_norm CROSS JOIN GENERATE_SERIES(0, 11) head ), sm_input AS ( SELECT head, h1.place AS x, h2.place AS y, INNER_PRODUCT(h1.q, h2.k) / 8 + CASE WHEN h2.place > h1.place THEN -1E10 ELSE 0 END AS value FROM heads h1 JOIN heads h2 USING (head) ), sm_diff AS ( SELECT head, x, y, value - MAX(value) OVER (PARTITION BY head, x) AS diff FROM sm_input ), sm_exp AS ( SELECT head, x, y, CASE WHEN diff < -745.13 THEN 0 ELSE EXP(diff) END AS e FROM sm_diff ), softmax AS ( SELECT head, x, y AS place, e / SUM(e) OVER (PARTITION BY head, x) AS value FROM sm_exp ), attention AS ( SELECT place, ARRAY_AGG(value ORDER BY head * 64 + ordinality)::VECTOR(768) AS values FROM ( SELECT head, x AS place, SUM(ARRAY_FILL(softmax.value, ARRAY[64])::VECTOR(64) * heads.v) AS values FROM softmax JOIN heads USING (head, place) GROUP BY head, x ) q CROSS JOIN LATERAL UNNEST(values::REAL[]) WITH ORDINALITY v (value, ordinality) GROUP BY place ), mha AS ( SELECT place, w.values + c_proj_b.values + embeddings.values AS values FROM ( SELECT attention.place, ARRAY_AGG(INNER_PRODUCT(attention.values, c_proj_w.values) ORDER BY c_proj_w.place)::VECTOR(768) AS values FROM attention CROSS JOIN c_proj_w GROUP BY attention.place ) w CROSS JOIN c_proj_b JOIN embeddings USING (place) ), ffn_norm AS ( SELECT place, agg.values * ln_2_g.values + ln_2_b.values AS values FROM ( SELECT place, norm.values FROM mha CROSS JOIN LATERAL ( SELECT AVG(value) AS mean, VAR_POP(value) AS variance FROM UNNEST(values::REAL[]) value ) agg CROSS JOIN LATERAL ( SELECT ARRAY_AGG((value - mean) / SQRT(variance + 1E-5) ORDER BY ordinality)::VECTOR(768) AS values FROM UNNEST(values::REAL[]) WITH ORDINALITY AS n(value, ordinality) ) norm ) agg CROSS JOIN ln_2_b CROSS JOIN ln_2_g ), ffn_a AS ( SELECT gelu.place, gelu.values FROM ( SELECT place, w.values + mlp_c_fc_b.values AS values FROM ( SELECT ffn_norm.place, ARRAY_AGG(INNER_PRODUCT(ffn_norm.values, mlp_c_fc_w.values) ORDER BY mlp_c_fc_w.place)::VECTOR(3072) AS values FROM ffn_norm CROSS JOIN mlp_c_fc_w GROUP BY ffn_norm.place ) w CROSS JOIN mlp_c_fc_b ) v CROSS JOIN LATERAL ( SELECT place, ARRAY_AGG(0.5 * value * (1 + TANH(0.797884560802 * (value + 0.044715 * value*value*value))) ORDER BY ordinality)::VECTOR(3072) AS values FROM UNNEST(values::REAL[]) WITH ORDINALITY n (value, ordinality) GROUP BY place ) gelu ), ffn AS ( SELECT place, w.values + mlp_c_proj_b.values + mha.values AS values FROM ( SELECT ffn_a.place, ARRAY_AGG(INNER_PRODUCT(ffn_a.values, mlp_c_proj_w.values) ORDER BY mlp_c_proj_w.place)::VECTOR(768) AS values FROM ffn_a CROSS JOIN mlp_c_proj_w GROUP BY ffn_a.place ) w CROSS JOIN mlp_c_proj_b JOIN mha USING (place) ) SELECT place, (SELECT STRING_AGG(TO_CHAR(n, 'S0.000'), ' ') || ' …' FROM UNNEST((values::REAL[])[:10]) AS n) AS q FROM ffn

Именно этот вывод получаем из первого блока GPT2.
Блоки
Операции, рассмотренные на предыдущих этапах, повторяются в каждом из слоёв (именуемых «блоками»). Блоки выстраиваются в виде конвейера, так, что вывод из предыдущего блока сразу подаётся на ввод следующему. У каждого из блоков – свой набор изученных параметров.
В SQL потребуется соединить блоки при помощи рекурсивного CTE.
Как только финальный блок выдаст значения, результат потребуется нормализовать при помощи изученного параметра ln_f.
Вот как в итоге будет выглядеть модель:
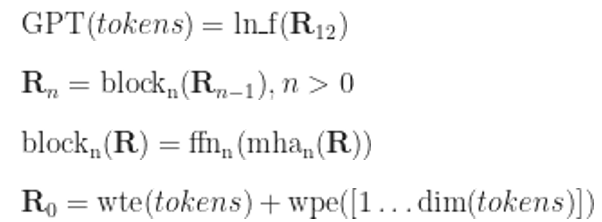
А вот как результат выглядит на SQL:
WITH RECURSIVE initial AS ( SELECT ARRAY[6307, 47701, 318, 1049] AS input ), hparams AS ( SELECT 12 AS n_block ), embeddings AS ( SELECT place, values FROM initial CROSS JOIN hparams CROSS JOIN LATERAL UNNEST(input) WITH ORDINALITY AS tokens (token, ordinality) CROSS JOIN LATERAL ( SELECT ordinality - 1 AS place ) o CROSS JOIN LATERAL ( SELECT wte.values + wpe.values AS values FROM wte CROSS JOIN wpe WHERE wte.token = tokens.token AND wpe.place = o.place ) embedding ), transform AS ( SELECT 0 AS block, place, values FROM embeddings UNION ALL ( WITH previous AS ( SELECT * FROM transform ) SELECT block + 1 AS block, transformed_layer.* FROM hparams CROSS JOIN LATERAL ( SELECT block FROM previous WHERE block < 12 LIMIT 1 ) q CROSS JOIN LATERAL ( WITH ln_2_b AS ( SELECT * FROM ln_2_b WHERE block = q.block ), ln_2_g AS ( SELECT * FROM ln_2_g WHERE block = q.block ), c_proj_w AS ( SELECT * FROM c_proj_w WHERE block = q.block ), c_proj_b AS ( SELECT * FROM c_proj_b WHERE block = q.block ), mlp_c_fc_w AS ( SELECT * FROM mlp_c_fc_w WHERE block = q.block ), mlp_c_fc_b AS ( SELECT * FROM mlp_c_fc_b WHERE block = q.block ), mlp_c_proj_w AS ( SELECT * FROM mlp_c_proj_w WHERE block = q.block ), mlp_c_proj_b AS ( SELECT * FROM mlp_c_proj_b WHERE block = q.block ), c_attn_w AS ( SELECT * FROM c_attn_w WHERE block = q.block ), c_attn_b AS ( SELECT * FROM c_attn_b WHERE block = q.block ), ln_1_g AS ( SELECT * FROM ln_1_g WHERE block = q.block ), ln_1_b AS ( SELECT * FROM ln_1_b WHERE block = q.block ), mha_norm AS ( SELECT place, mm.values + c_attn_b.values AS values FROM ( SELECT place, ARRAY_AGG(INNER_PRODUCT(c_attn_w.values, layer_norm.values) ORDER BY y)::VECTOR(2304) AS values FROM ( SELECT place, agg.values * ln_1_g.values + ln_1_b.values AS values FROM ( SELECT place, norm.values FROM previous CROSS JOIN LATERAL ( SELECT AVG(value) AS mean, VAR_POP(value) AS variance FROM UNNEST(values::REAL[]) value ) agg CROSS JOIN LATERAL ( SELECT ARRAY_AGG((value - mean) / SQRT(variance + 1E-5) ORDER BY ordinality)::VECTOR(768) AS values FROM UNNEST(values::REAL[]) WITH ORDINALITY AS n(value, ordinality) ) norm ) agg CROSS JOIN ln_1_b CROSS JOIN ln_1_g ) layer_norm CROSS JOIN c_attn_w GROUP BY place ) mm CROSS JOIN c_attn_b ), heads AS ( SELECT place, head, (values::REAL[])[(head * 64 + 1):(head * 64 + 64)]::VECTOR(64) AS q, (values::REAL[])[(head * 64 + 1 + 768):(head * 64 + 64 + 768)]::VECTOR(64) AS k, (values::REAL[])[(head * 64 + 1 + 1536):(head * 64 + 64 + 1536)]::VECTOR(64) AS v FROM mha_norm CROSS JOIN GENERATE_SERIES(0, 11) head ), sm_input AS ( SELECT head, h1.place AS x, h2.place AS y, INNER_PRODUCT(h1.q, h2.k) / 8 + CASE WHEN h2.place > h1.place THEN -1E10 ELSE 0 END AS value FROM heads h1 JOIN heads h2 USING (head) ), sm_diff AS ( SELECT head, x, y, value - MAX(value) OVER (PARTITION BY head, x) AS diff FROM sm_input ), sm_exp AS ( SELECT head, x, y, CASE WHEN diff < -745.13 THEN 0 ELSE EXP(diff) END AS e FROM sm_diff ), softmax AS ( SELECT head, x, y AS place, e / SUM(e) OVER (PARTITION BY head, x) AS value FROM sm_exp ), attention AS ( SELECT place, ARRAY_AGG(value ORDER BY head * 64 + ordinality)::VECTOR(768) AS values FROM ( SELECT head, x AS place, SUM(ARRAY_FILL(softmax.value, ARRAY[64])::VECTOR(64) * heads.v) AS values FROM softmax JOIN heads USING (head, place) GROUP BY head, x ) q CROSS JOIN LATERAL UNNEST(values::REAL[]) WITH ORDINALITY v (value, ordinality) GROUP BY place ), mha AS ( SELECT place, w.values + c_proj_b.values + previous.values AS values FROM ( SELECT attention.place, ARRAY_AGG(INNER_PRODUCT(attention.values, c_proj_w.values) ORDER BY c_proj_w.place)::VECTOR(768) AS values FROM attention CROSS JOIN c_proj_w GROUP BY attention.place ) w CROSS JOIN c_proj_b JOIN previous USING (place) ), ffn_norm AS ( SELECT place, agg.values * ln_2_g.values + ln_2_b.values AS values FROM ( SELECT place, norm.values FROM mha CROSS JOIN LATERAL ( SELECT AVG(value) AS mean, VAR_POP(value) AS variance FROM UNNEST(values::REAL[]) value ) agg CROSS JOIN LATERAL ( SELECT ARRAY_AGG((value - mean) / SQRT(variance + 1E-5) ORDER BY ordinality)::VECTOR(768) AS values FROM UNNEST(values::REAL[]) WITH ORDINALITY AS n(value, ordinality) ) norm ) agg CROSS JOIN ln_2_b CROSS JOIN ln_2_g ), ffn_a AS ( SELECT gelu.place, gelu.values FROM ( SELECT place, w.values + mlp_c_fc_b.values AS values FROM ( SELECT ffn_norm.place, ARRAY_AGG(INNER_PRODUCT(ffn_norm.values, mlp_c_fc_w.values) ORDER BY mlp_c_fc_w.place)::VECTOR(3072) AS values FROM ffn_norm CROSS JOIN mlp_c_fc_w GROUP BY ffn_norm.place ) w CROSS JOIN mlp_c_fc_b ) v CROSS JOIN LATERAL ( SELECT place, ARRAY_AGG(0.5 * value * (1 + TANH(0.797884560802 * (value + 0.044715 * value*value*value))) ORDER BY ordinality)::VECTOR(3072) AS values FROM UNNEST(values::REAL[]) WITH ORDINALITY n (value, ordinality) GROUP BY place ) gelu ), ffn AS ( SELECT place, w.values + mlp_c_proj_b.values + mha.values AS values FROM ( SELECT ffn_a.place, ARRAY_AGG(INNER_PRODUCT(ffn_a.values, mlp_c_proj_w.values) ORDER BY mlp_c_proj_w.place)::VECTOR(768) AS values FROM ffn_a CROSS JOIN mlp_c_proj_w GROUP BY ffn_a.place ) w CROSS JOIN mlp_c_proj_b JOIN mha USING (place) ) SELECT * FROM ffn ) transformed_layer ) ), block_output AS ( SELECT * FROM hparams JOIN transform ON transform.block = n_block ), ln_f AS ( SELECT place, norm.values * ln_f_g.values + ln_f_b.values AS values FROM block_output CROSS JOIN LATERAL ( SELECT AVG(value) AS mean, VAR_POP(value) AS variance FROM UNNEST(values::REAL[]) AS n(value) ) agg CROSS JOIN LATERAL ( SELECT ARRAY_AGG((value - mean) / SQRT(variance + 1E-5) ORDER BY ordinality)::VECTOR(768) AS values FROM UNNEST(values::REAL[]) WITH ORDINALITY AS n (value, ordinality) ) norm CROSS JOIN ln_f_b CROSS JOIN ln_f_g ) SELECT place, (SELECT STRING_AGG(TO_CHAR(n, 'S0.000'), ' ') || ' …' FROM UNNEST((values::REAL[])[:10]) AS n) AS q FROM ln_f

Это вывод модели.
Четвёртый вектор – это и есть фактическое представление следующего токена, предсказанного моделью. Нам просто нужно отобразить его обратно на токены.
Токены
У нас уже есть векторное представление (768-мерное), в котором, согласно модели, заключены семантика и грамматика наиболее вероятного продолжения промпта. Теперь нам нужно отобразить его обратно на токен.
Одна из первых операций, совершаемых моделью – это отображение токенов на их векторные представления. Эта операция делается при помощи матрицы wpe размером 50257×768. Той же самой матрицей нам потребуется воспользоваться, чтобы отобразить векторное представление обратно на токен.
Проблема в том, что строго обратное отображение выполнить невозможно: (вероятно) векторное представление не будет совпадать ни с одной из строк в матрице. ��оэтому нам придётся найти токен, который «ближе всего» к векторному представлению.
Поскольку (как мы надеемся), в измерениях векторных представлений заключены некоторые семантические и грамматические аспекты токена, необходимо сопоставить их как можно точнее. Один из способов консолидировать «степень близости» каждого из измерений – вычислить скалярное произведение двух векторных представлений. Чем выше будет это значение, тем ближе токен к прогнозу.
Для этого умножим векторное представление на матрицу wte. В результате получим матрицу из одного столбца и 50257 строк. Каждое значение в этом результате будет произведением спрогнозированного вектора и векторного представления токена. Чем выше это число, тем вероятнее, что токен станет продолжением промпта.
Чтобы выбрать следующий токен, нужно просто преобразовать значения сходства в значения вероятности. Для этого нам пригодится старая добрая функция softmax (та самая, при помощи которой мы уже нормализовали веса внимания).
Почему стоит использовать softmax для работы с вероятностями?
Softmax – это удобное свойство аксиомы выбора Льюса. Оно таково: относительная вероятность двух вариантов не зависит от наличия прочих вероятностных вариантов. Если вариант A вдвое вероятнее варианта B, то это соотношение не зависит от наличия или отсутствия других вариантов (хотя, конечно, абсолютные значения при этом могут измениться).
Вектор скалярных произведений («логит» в терминологии ИИ) содержит произвольные значения, которые могут не укладываться в какую-либо шкалу. Если балл A выше, чем балл B, то известно, что A вероятнее – а больше ничего не известно. Можно подкорректировать входные значения softmax так, как нам угодно, главное, соблюдать их порядок (более крупные значения остаются более крупными).
Распространённый подход, позволяющий этого добиться – нормализация значений путём вычитания наибольшего значения из каждого значения в множестве (так что наибольшее значение становится равным 0, а все остальные – отрицательным числам). Затем берём фиксированное количество наивысших значений (скажем, топ-5 или топ-10). Наконец, перед передачей всех значений softmax умножаем их на константу.
Количество наивысших значений, с которым мы работаем, обычно называется top_n, а множитель-константа (вернее, обратное ему число) называется «температурой» (Т). Чем выше температура, тем более гладкое распределение вероятностей у нас получится, и тем выше вероятность, что на место продолжения будет выбран не первый попавшийся токен.
Формула для расчёта вероятностей токенов
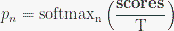
где scores — это множество из наивысших top_n баллов.
Почему этот показатель называется "температурой"
Функция softmax также называется распределение Больцмана. Она широко используется в физике. Среди прочего, на ней основана барометрическая формула, по которой рассчитывается изменение плотности воздуха в зависимости от высоты.
Как известно, тёплый воздух поднимается вверх и распределяется на сравнительно большой высоте. В горячем воздухе сравнительно высока вероятность, что молекула от частых столкновений с другими молекулами заберётся на такую высоту, куда в ином случае бы не попала. В отличие от ситуации с более холодными температурами, плотность воздуха увеличивается на больших высотах и падает на уровне моря.
Сравните, как воздух движется при разных температурах:
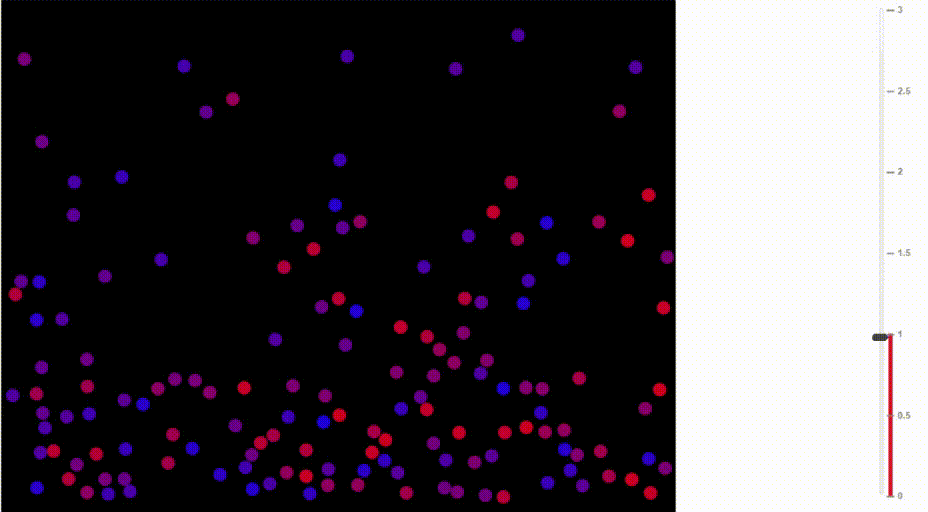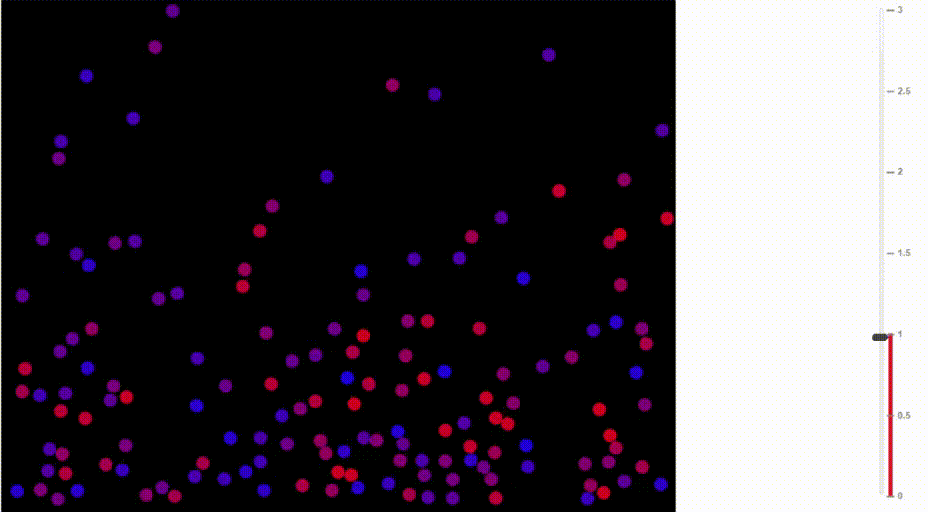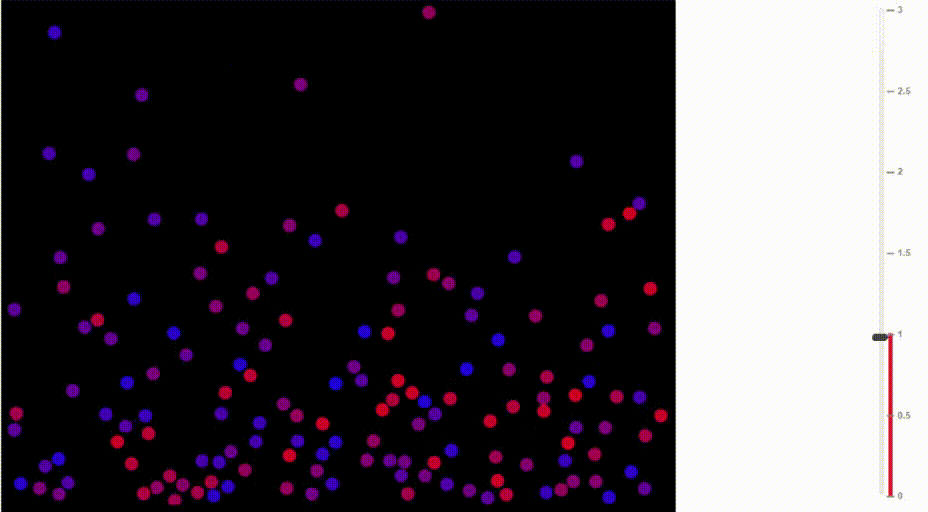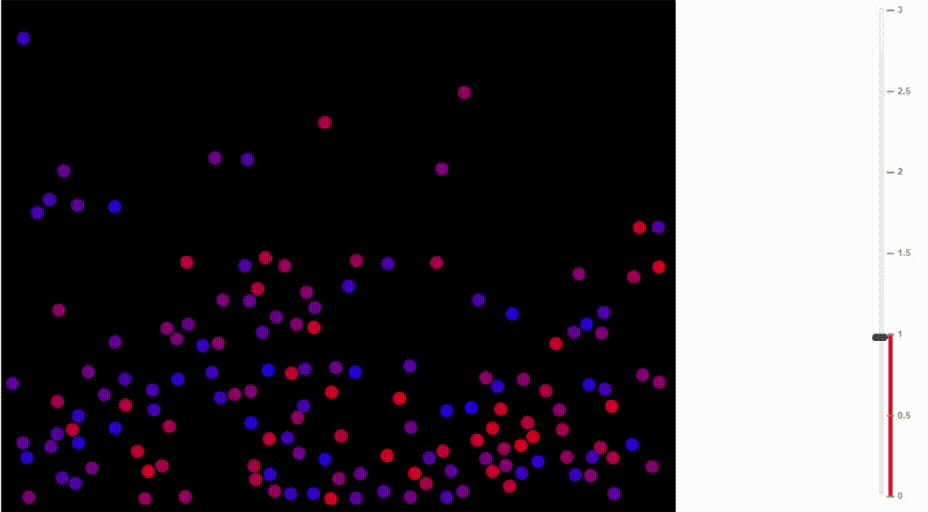
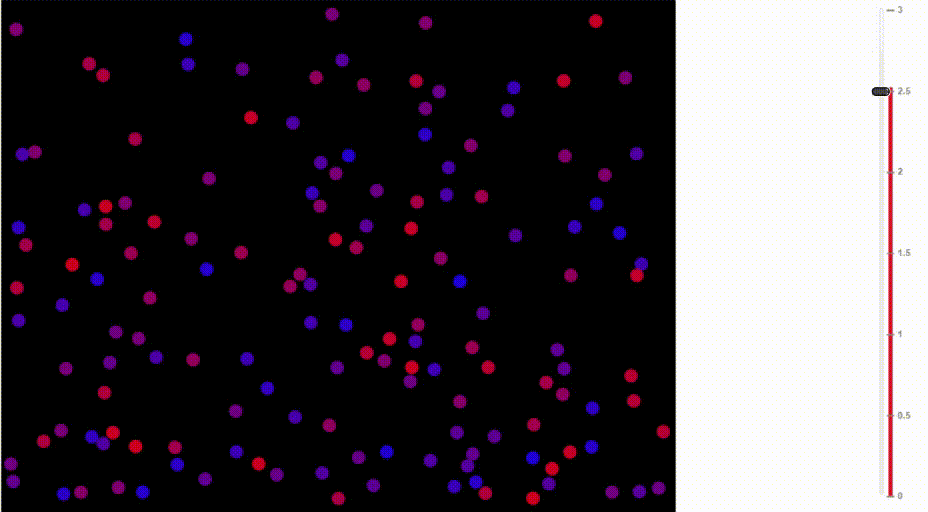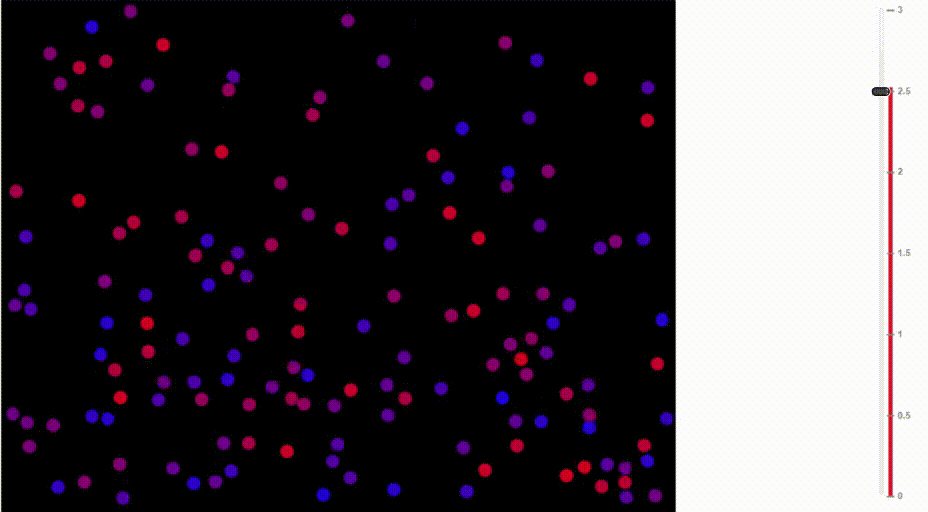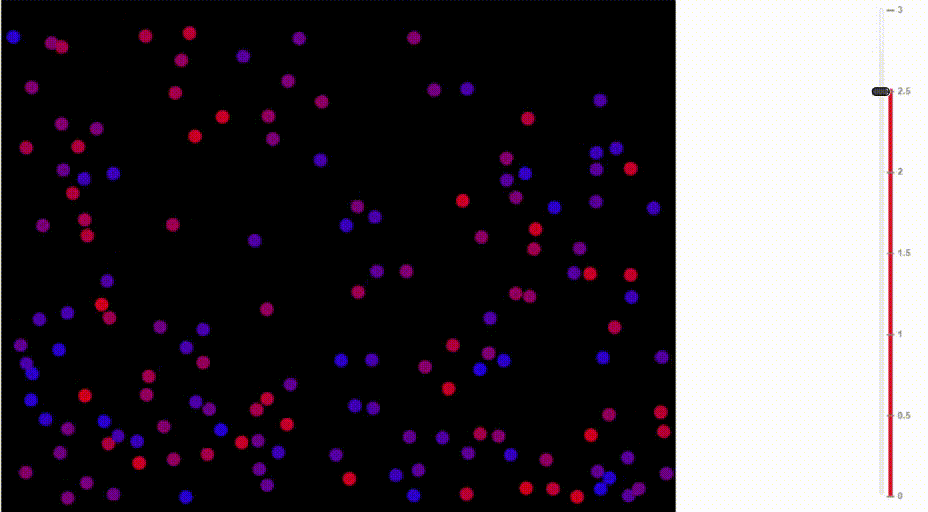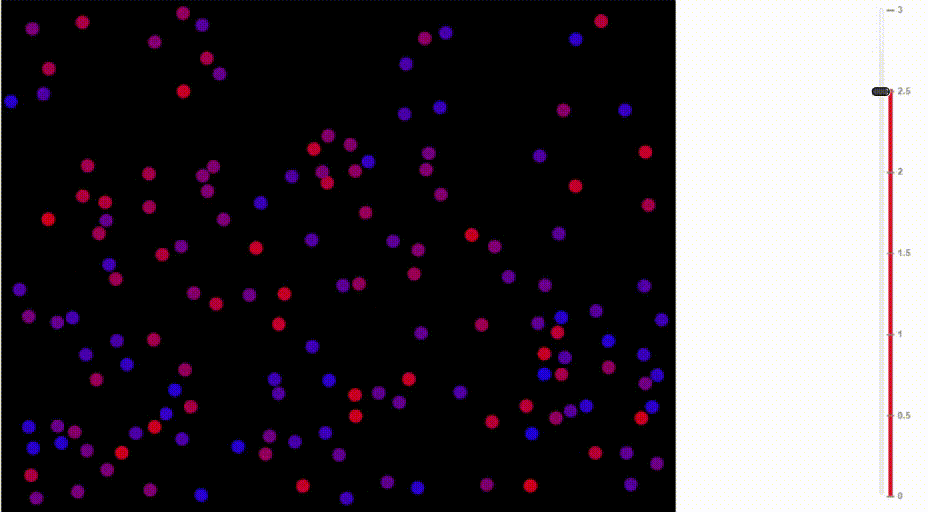
Иллюстрация Доминика Форда, Bouncing Balls and the Boltzmann Distribution
Аналогично, в рассматриваемом нами примере, чем больше «температура», тем выше вероятность, что будет выбран не самый очевидный токен (разумеется, за счёт наиболее очевидных). Логический вывод становится менее предсказуемым и более «творческим».
Давайте выразим всё это на SQL. У нас был промпт «PostgreSQL is great». Вот первые 5 токенов, которые, в соответствии с этой моделью, являются наиболее вероятными продолжениями этой фразы. Показаны их вероятности при разной температуре:
WITH RECURSIVE initial AS ( SELECT ARRAY[6307, 47701, 318, 1049] AS input ), hparams AS ( SELECT 12 AS n_block, 5 AS top_n, ARRAY_LENGTH(input, 1) AS n_seq FROM initial ), embeddings AS ( SELECT place, values FROM initial CROSS JOIN hparams CROSS JOIN LATERAL UNNEST(input) WITH ORDINALITY AS tokens (token, ordinality) CROSS JOIN LATERAL ( SELECT ordinality - 1 AS place ) o CROSS JOIN LATERAL ( SELECT wte.values + wpe.values AS values FROM wte CROSS JOIN wpe WHERE wte.token = tokens.token AND wpe.place = o.place ) embedding ), transform AS ( SELECT 0 AS block, place, values FROM embeddings UNION ALL ( WITH previous AS ( SELECT * FROM transform ) SELECT block + 1 AS block, transformed_layer.* FROM hparams CROSS JOIN LATERAL ( SELECT block FROM previous WHERE block < 12 LIMIT 1 ) q CROSS JOIN LATERAL ( WITH ln_2_b AS ( SELECT * FROM ln_2_b WHERE block = q.block ), ln_2_g AS ( SELECT * FROM ln_2_g WHERE block = q.block ), c_proj_w AS ( SELECT * FROM c_proj_w WHERE block = q.block ), c_proj_b AS ( SELECT * FROM c_proj_b WHERE block = q.block ), mlp_c_fc_w AS ( SELECT * FROM mlp_c_fc_w WHERE block = q.block ), mlp_c_fc_b AS ( SELECT * FROM mlp_c_fc_b WHERE block = q.block ), mlp_c_proj_w AS ( SELECT * FROM mlp_c_proj_w WHERE block = q.block ), mlp_c_proj_b AS ( SELECT * FROM mlp_c_proj_b WHERE block = q.block ), c_attn_w AS ( SELECT * FROM c_attn_w WHERE block = q.block ), c_attn_b AS ( SELECT * FROM c_attn_b WHERE block = q.block ), ln_1_g AS ( SELECT * FROM ln_1_g WHERE block = q.block ), ln_1_b AS ( SELECT * FROM ln_1_b WHERE block = q.block ), mha_norm AS ( SELECT place, mm.values + c_attn_b.values AS values FROM ( SELECT place, ARRAY_AGG(INNER_PRODUCT(c_attn_w.values, layer_norm.values) ORDER BY y)::VECTOR(2304) AS values FROM ( SELECT place, agg.values * ln_1_g.values + ln_1_b.values AS values FROM ( SELECT place, norm.values FROM previous CROSS JOIN LATERAL ( SELECT AVG(value) AS mean, VAR_POP(value) AS variance FROM UNNEST(values::REAL[]) value ) agg CROSS JOIN LATERAL ( SELECT ARRAY_AGG((value - mean) / SQRT(variance + 1E-5) ORDER BY ordinality)::VECTOR(768) AS values FROM UNNEST(values::REAL[]) WITH ORDINALITY AS n(value, ordinality) ) norm ) agg CROSS JOIN ln_1_b CROSS JOIN ln_1_g ) layer_norm CROSS JOIN c_attn_w GROUP BY place ) mm CROSS JOIN c_attn_b ), heads AS ( SELECT place, head, (values::REAL[])[(head * 64 + 1):(head * 64 + 64)]::VECTOR(64) AS q, (values::REAL[])[(head * 64 + 1 + 768):(head * 64 + 64 + 768)]::VECTOR(64) AS k, (values::REAL[])[(head * 64 + 1 + 1536):(head * 64 + 64 + 1536)]::VECTOR(64) AS v FROM mha_norm CROSS JOIN GENERATE_SERIES(0, 11) head ), sm_input AS ( SELECT head, h1.place AS x, h2.place AS y, INNER_PRODUCT(h1.q, h2.k) / 8 + CASE WHEN h2.place > h1.place THEN -1E10 ELSE 0 END AS value FROM heads h1 JOIN heads h2 USING (head) ), sm_diff AS ( SELECT head, x, y, value - MAX(value) OVER (PARTITION BY head, x) AS diff FROM sm_input ), sm_exp AS ( SELECT head, x, y, CASE WHEN diff < -745.13 THEN 0 ELSE EXP(diff) END AS e FROM sm_diff ), softmax AS ( SELECT head, x, y AS place, e / SUM(e) OVER (PARTITION BY head, x) AS value FROM sm_exp ), attention AS ( SELECT place, ARRAY_AGG(value ORDER BY head * 64 + ordinality)::VECTOR(768) AS values FROM ( SELECT head, x AS place, SUM(ARRAY_FILL(softmax.value, ARRAY[64])::VECTOR(64) * heads.v) AS values FROM softmax JOIN heads USING (head, place) GROUP BY head, x ) q CROSS JOIN LATERAL UNNEST(values::REAL[]) WITH ORDINALITY v (value, ordinality) GROUP BY place ), mha AS ( SELECT place, w.values + c_proj_b.values + previous.values AS values FROM ( SELECT attention.place, ARRAY_AGG(INNER_PRODUCT(attention.values, c_proj_w.values) ORDER BY c_proj_w.place)::VECTOR(768) AS values FROM attention CROSS JOIN c_proj_w GROUP BY attention.place ) w CROSS JOIN c_proj_b JOIN previous USING (place) ), ffn_norm AS ( SELECT place, agg.values * ln_2_g.values + ln_2_b.values AS values FROM ( SELECT place, norm.values FROM mha CROSS JOIN LATERAL ( SELECT AVG(value) AS mean, VAR_POP(value) AS variance FROM UNNEST(values::REAL[]) value ) agg CROSS JOIN LATERAL ( SELECT ARRAY_AGG((value - mean) / SQRT(variance + 1E-5) ORDER BY ordinality)::VECTOR(768) AS values FROM UNNEST(values::REAL[]) WITH ORDINALITY AS n(value, ordinality) ) norm ) agg CROSS JOIN ln_2_b CROSS JOIN ln_2_g ), ffn_a AS ( SELECT gelu.place, gelu.values FROM ( SELECT place, w.values + mlp_c_fc_b.values AS values FROM ( SELECT ffn_norm.place, ARRAY_AGG(INNER_PRODUCT(ffn_norm.values, mlp_c_fc_w.values) ORDER BY mlp_c_fc_w.place)::VECTOR(3072) AS values FROM ffn_norm CROSS JOIN mlp_c_fc_w GROUP BY ffn_norm.place ) w CROSS JOIN mlp_c_fc_b ) v CROSS JOIN LATERAL ( SELECT place, ARRAY_AGG(0.5 * value * (1 + TANH(0.797884560802 * (value + 0.044715 * value*value*value))) ORDER BY ordinality)::VECTOR(3072) AS values FROM UNNEST(values::REAL[]) WITH ORDINALITY n (value, ordinality) GROUP BY place ) gelu ), ffn AS ( SELECT place, w.values + mlp_c_proj_b.values + mha.values AS values FROM ( SELECT ffn_a.place, ARRAY_AGG(INNER_PRODUCT(ffn_a.values, mlp_c_proj_w.values) ORDER BY mlp_c_proj_w.place)::VECTOR(768) AS values FROM ffn_a CROSS JOIN mlp_c_proj_w GROUP BY ffn_a.place ) w CROSS JOIN mlp_c_proj_b JOIN mha USING (place) ) SELECT * FROM ffn ) transformed_layer ) ), block_output AS ( SELECT * FROM hparams JOIN transform ON transform.block = n_block ), ln_f AS ( SELECT place, norm.values * ln_f_g.values + ln_f_b.values AS values FROM block_output CROSS JOIN LATERAL ( SELECT AVG(value) AS mean, VAR_POP(value) AS variance FROM UNNEST(values::REAL[]) AS n(value) ) agg CROSS JOIN LATERAL ( SELECT ARRAY_AGG((value - mean) / SQRT(variance + 1E-5) ORDER BY ordinality)::VECTOR(768) AS values FROM UNNEST(values::REAL[]) WITH ORDINALITY AS n (value, ordinality) ) norm CROSS JOIN ln_f_b CROSS JOIN ln_f_g ), logits AS ( SELECT logits.* FROM hparams CROSS JOIN LATERAL ( SELECT token, INNER_PRODUCT(ln_f.values, wte.values) AS value FROM ln_f CROSS JOIN wte WHERE ln_f.place = n_seq - 1 ORDER BY value DESC LIMIT (top_n) ) logits ), temperatures (temperature) AS ( VALUES (0.5), (1), (2) ), tokens AS ( SELECT token, value, softmax, temperature FROM temperatures CROSS JOIN LATERAL ( SELECT *, (e / SUM(e) OVER ()) AS softmax FROM ( SELECT *, (value - MAX(value) OVER ()) / temperature AS diff FROM logits ) exp_x CROSS JOIN LATERAL ( SELECT CASE WHEN diff < -745.13 THEN 0 ELSE EXP(diff) END AS e ) exp ) q ) SELECT token, cluster, TO_CHAR(t1.value, 'S00.000') AS score, TO_CHAR(t1.softmax, '0.00') AS "temperature = 0.5", TO_CHAR(t2.softmax, '0.00') AS "temperature = 1", TO_CHAR(t3.softmax, '0.00') AS "temperature = 2" FROM ( SELECT * FROM tokens WHERE temperature = 0.5 ) t1 JOIN ( SELECT * FROM tokens WHERE temperature = 1 ) t2 USING (token) JOIN ( SELECT * FROM tokens WHERE temperature = 2 ) t3 USING (token) JOIN tokenizer USING (token)

Логический вывод
Вот мы и готовы перейти к реальному логическому выводу: запустить модель, выбрать токен в соответствии с полученной вероятностью, добавить токен к промпту и повторять этот процесс до тех пор, пока не будет сгенерировано достаточное количество токенов.
Как было показано выше, сама большая языковая модель является детерминированной. Это просто последовательные перемножения матриц и другие математические операции, производимые над заранее определёнными константами. Пока промпт и такие гиперпараметры как температура и топ-N остаются неизменными, вывод также остаётся неизменным.
Единственный недетерминированный процесс в данном случае – это выбор токена. В нём заложена (переменная) степень случайности. Вот почему чатботы, основанные на GPT, могут давать разные ответы на один и тот же промпт.
Воспользуемся в качестве промпта фразой «Happy New Year! I wish» и прикажем модели сгенерировать 10 новых токенов для этого промпта. Температуру установим в 2, а top_n в 5.
У меня на компьютере на этот запрос уходит 2 минуты и 44 секунды. Вот такой вывод получается:
SELECT SETSEED(0.20231231); WITH RECURSIVE input AS ( SELECT 'Happy New Year! I wish you' AS prompt, 10 AS threshold, 2 AS temperature, 1 AS top_n ), clusters AS ( SELECT part_position, bpe.* FROM input CROSS JOIN LATERAL REGEXP_MATCHES(prompt, '''s|''t|''re|''ve|''m|''ll|''d| ?\w+| ?\d+| ?[^\s\w\d]+|\s+(?!\S)|\s+', 'g') WITH ORDINALITY AS rm (part, part_position) CROSS JOIN LATERAL ( WITH RECURSIVE bpe AS ( SELECT (n + 1)::BIGINT AS position, character, TRUE AS continue FROM CONVERT_TO(part[1], 'UTF-8') AS bytes CROSS JOIN LATERAL GENERATE_SERIES(0, LENGTH(bytes) - 1) AS n JOIN encoder ON byte = GET_BYTE(bytes, n) UNION ALL ( WITH RECURSIVE base AS ( SELECT * FROM bpe WHERE continue ), bn AS ( SELECT ROW_NUMBER() OVER (ORDER BY position) AS position, continue, character, character || LEAD(character) OVER (ORDER BY position) AS cluster FROM base ), top_rank AS ( SELECT tokenizer.* FROM bn CROSS JOIN LATERAL ( SELECT * FROM tokenizer WHERE tokenizer.cluster = bn.cluster LIMIT 1 ) tokenizer ORDER BY token LIMIT 1 ), breaks AS ( SELECT 0::BIGINT AS position, 1 AS length UNION ALL SELECT bn.position, CASE WHEN token IS NULL THEN 1 ELSE 2 END FROM breaks JOIN bn ON bn.position = breaks.position + length LEFT JOIN top_rank USING (cluster) ) SELECT position, character, token IS NOT NULL FROM breaks LEFT JOIN top_rank ON 1 = 1 CROSS JOIN LATERAL ( SELECT STRING_AGG(character, '' ORDER BY position) AS character FROM bn WHERE bn.position >= breaks.position AND bn.position < breaks.position + length ) bn WHERE position > 0 ) ) SELECT position, character AS cluster FROM bpe WHERE NOT continue ) bpe ), tokens AS ( SELECT ARRAY_AGG(token ORDER BY part_position, position) AS input FROM clusters JOIN tokenizer USING (cluster) ), gpt AS ( SELECT input, ARRAY_LENGTH(input, 1) AS original_length FROM tokens UNION ALL SELECT input || next_token.token, original_length FROM gpt CROSS JOIN input CROSS JOIN LATERAL ( WITH RECURSIVE hparams AS ( SELECT ARRAY_LENGTH(input, 1) AS n_seq, 12 AS n_block ), embeddings AS ( SELECT place, values FROM hparams CROSS JOIN LATERAL UNNEST(input) WITH ORDINALITY AS tokens (token, ordinality) CROSS JOIN LATERAL ( SELECT ordinality - 1 AS place ) o CROSS JOIN LATERAL ( SELECT wte.values + wpe.values AS values FROM wte CROSS JOIN wpe WHERE wte.token = tokens.token AND wpe.place = o.place ) embedding ), transform AS ( SELECT 0 AS block, place, values FROM embeddings UNION ALL ( WITH previous AS ( SELECT * FROM transform ) SELECT block + 1 AS block, transformed_layer.* FROM hparams CROSS JOIN LATERAL ( SELECT block FROM previous WHERE block < 12 LIMIT 1 ) q CROSS JOIN LATERAL ( WITH ln_2_b AS ( SELECT * FROM ln_2_b WHERE block = q.block ), ln_2_g AS ( SELECT * FROM ln_2_g WHERE block = q.block ), c_proj_w AS ( SELECT * FROM c_proj_w WHERE block = q.block ), c_proj_b AS ( SELECT * FROM c_proj_b WHERE block = q.block ), mlp_c_fc_w AS ( SELECT * FROM mlp_c_fc_w WHERE block = q.block ), mlp_c_fc_b AS ( SELECT * FROM mlp_c_fc_b WHERE block = q.block ), mlp_c_proj_w AS ( SELECT * FROM mlp_c_proj_w WHERE block = q.block ), mlp_c_proj_b AS ( SELECT * FROM mlp_c_proj_b WHERE block = q.block ), c_attn_w AS ( SELECT * FROM c_attn_w WHERE block = q.block ), c_attn_b AS ( SELECT * FROM c_attn_b WHERE block = q.block ), ln_1_g AS ( SELECT * FROM ln_1_g WHERE block = q.block ), ln_1_b AS ( SELECT * FROM ln_1_b WHERE block = q.block ), mha_norm AS ( SELECT place, mm.values + c_attn_b.values AS values FROM ( SELECT place, ARRAY_AGG(INNER_PRODUCT(c_attn_w.values, layer_norm.values) ORDER BY y)::VECTOR(2304) AS values FROM ( SELECT place, agg.values * ln_1_g.values + ln_1_b.values AS values FROM ( SELECT place, norm.values FROM previous CROSS JOIN LATERAL ( SELECT AVG(value) AS mean, VAR_POP(value) AS variance FROM UNNEST(values::REAL[]) value ) agg CROSS JOIN LATERAL ( SELECT ARRAY_AGG((value - mean) / SQRT(variance + 1E-5) ORDER BY ordinality)::VECTOR(768) AS values FROM UNNEST(values::REAL[]) WITH ORDINALITY AS n(value, ordinality) ) norm ) agg CROSS JOIN ln_1_b CROSS JOIN ln_1_g ) layer_norm CROSS JOIN c_attn_w GROUP BY place ) mm CROSS JOIN c_attn_b ), heads AS ( SELECT place, head, (values::REAL[])[(head * 64 + 1):(head * 64 + 64)]::VECTOR(64) AS q, (values::REAL[])[(head * 64 + 1 + 768):(head * 64 + 64 + 768)]::VECTOR(64) AS k, (values::REAL[])[(head * 64 + 1 + 1536):(head * 64 + 64 + 1536)]::VECTOR(64) AS v FROM mha_norm CROSS JOIN GENERATE_SERIES(0, 11) head ), sm_input AS ( SELECT head, h1.place AS x, h2.place AS y, INNER_PRODUCT(h1.q, h2.k) / 8 + CASE WHEN h2.place > h1.place THEN -1E10 ELSE 0 END AS value FROM heads h1 JOIN heads h2 USING (head) ), sm_diff AS ( SELECT head, x, y, value - MAX(value) OVER (PARTITION BY head, x) AS diff FROM sm_input ), sm_exp AS ( SELECT head, x, y, CASE WHEN diff < -745.13 THEN 0 ELSE EXP(diff) END AS e FROM sm_diff ), softmax AS ( SELECT head, x, y AS place, e / SUM(e) OVER (PARTITION BY head, x) AS value FROM sm_exp ), attention AS ( SELECT place, ARRAY_AGG(value ORDER BY head * 64 + ordinality)::VECTOR(768) AS values FROM ( SELECT head, x AS place, SUM(ARRAY_FILL(softmax.value, ARRAY[64])::VECTOR(64) * heads.v) AS values FROM softmax JOIN heads USING (head, place) GROUP BY head, x ) q CROSS JOIN LATERAL UNNEST(values::REAL[]) WITH ORDINALITY v (value, ordinality) GROUP BY place ), mha AS ( SELECT place, w.values + c_proj_b.values + previous.values AS values FROM ( SELECT attention.place, ARRAY_AGG(INNER_PRODUCT(attention.values, c_proj_w.values) ORDER BY c_proj_w.place)::VECTOR(768) AS values FROM attention CROSS JOIN c_proj_w GROUP BY attention.place ) w CROSS JOIN c_proj_b JOIN previous USING (place) ), ffn_norm AS ( SELECT place, agg.values * ln_2_g.values + ln_2_b.values AS values FROM ( SELECT place, norm.values FROM mha CROSS JOIN LATERAL ( SELECT AVG(value) AS mean, VAR_POP(value) AS variance FROM UNNEST(values::REAL[]) value ) agg CROSS JOIN LATERAL ( SELECT ARRAY_AGG((value - mean) / SQRT(variance + 1E-5) ORDER BY ordinality)::VECTOR(768) AS values FROM UNNEST(values::REAL[]) WITH ORDINALITY AS n(value, ordinality) ) norm ) agg CROSS JOIN ln_2_b CROSS JOIN ln_2_g ), ffn_a AS ( SELECT gelu.place, gelu.values FROM ( SELECT place, w.values + mlp_c_fc_b.values AS values FROM ( SELECT ffn_norm.place, ARRAY_AGG(INNER_PRODUCT(ffn_norm.values, mlp_c_fc_w.values) ORDER BY mlp_c_fc_w.place)::VECTOR(3072) AS values FROM ffn_norm CROSS JOIN mlp_c_fc_w GROUP BY ffn_norm.place ) w CROSS JOIN mlp_c_fc_b ) v CROSS JOIN LATERAL ( SELECT place, ARRAY_AGG(0.5 * value * (1 + TANH(0.797884560802 * (value + 0.044715 * value*value*value))) ORDER BY ordinality)::VECTOR(3072) AS values FROM UNNEST(values::REAL[]) WITH ORDINALITY n (value, ordinality) GROUP BY place ) gelu ), ffn AS ( SELECT place, w.values + mlp_c_proj_b.values + mha.values AS values FROM ( SELECT ffn_a.place, ARRAY_AGG(INNER_PRODUCT(ffn_a.values, mlp_c_proj_w.values) ORDER BY mlp_c_proj_w.place)::VECTOR(768) AS values FROM ffn_a CROSS JOIN mlp_c_proj_w GROUP BY ffn_a.place ) w CROSS JOIN mlp_c_proj_b JOIN mha USING (place) ) SELECT * FROM ffn ) transformed_layer ) ), block_output AS ( SELECT * FROM hparams JOIN transform ON transform.block = n_block ), ln_f AS ( SELECT place, norm.values * ln_f_g.values + ln_f_b.values AS values FROM block_output CROSS JOIN LATERAL ( SELECT AVG(value) AS mean, VAR_POP(value) AS variance FROM UNNEST(values::REAL[]) AS n(value) ) agg CROSS JOIN LATERAL ( SELECT ARRAY_AGG((value - mean) / SQRT(variance + 1E-5) ORDER BY ordinality)::VECTOR(768) AS values FROM UNNEST(values::REAL[]) WITH ORDINALITY AS n (value, ordinality) ) norm CROSS JOIN ln_f_b CROSS JOIN ln_f_g ), logits AS ( SELECT token, INNER_PRODUCT(ln_f.values, wte.values) AS value FROM hparams JOIN ln_f ON ln_f.place = n_seq - 1 CROSS JOIN wte ORDER BY value DESC LIMIT (top_n) ), tokens AS ( SELECT token, high - softmax AS low, high FROM ( SELECT *, SUM(softmax) OVER (ORDER BY softmax) AS high FROM ( SELECT *, (e / SUM(e) OVER ()) AS softmax FROM ( SELECT *, (value - MAX(value) OVER ()) / temperature AS diff FROM logits ) exp_x CROSS JOIN LATERAL ( SELECT CASE WHEN diff < -745.13 THEN 0 ELSE EXP(diff) END AS e ) exp ) q ) q ), next_token AS ( SELECT * FROM ( SELECT RANDOM() AS rnd ) r CROSS JOIN LATERAL ( SELECT * FROM tokens WHERE rnd >= low AND rnd < high ) nt ) SELECT * FROM next_token ) next_token WHERE ARRAY_LENGTH(input, 1) < original_length + threshold AND next_token.token <> 50256 ), output AS ( SELECT CONVERT_FROM(STRING_AGG(SET_BYTE('\x00', 0, byte), '' ORDER BY position), 'UTF8') AS response FROM ( SELECT STRING_AGG(cluster, '' ORDER BY ordinality) AS response FROM input JOIN gpt ON ARRAY_LENGTH(input, 1) = original_length + threshold CROSS JOIN LATERAL UNNEST(input) WITH ORDINALITY n (token, ordinality) JOIN tokenizer USING (token) ) q CROSS JOIN LATERAL STRING_TO_TABLE(response, NULL) WITH ORDINALITY n (character, position) JOIN encoder USING (character) ) SELECT * FROM output

ИИ со своей работой справился отлично. Я искренне желаю вам всего самого лучшего в наступившем году!
Все запросы и код для установки выложены в следующем репозитории на GitHub: quassnoi/explain-extended-2024.