
«Жить эффективно — значит жить с адекватной информацией» (Норберт Винер)
«Управление сложностью является сущностью компьютерного программирования» (Брайан Керниган)
«По мере того, как сложность возрастает, точные утверждения теряют значимость, а значимые утверждения теряют точность» (Лотфи Заде)
«Глупцы игнорируют сложность. Прагматики терпят её. Некоторые могут избегать её. Гении её устраняют» (Алан Перлис)
Это продолжение статьи «Информация об информации», где я показал, что информация – физическая величина, не имеющая ничего общего с духом, сознанием, «информационным полем» и другими эзотерическими понятиями. Но среди философов и мистиков бытует мнение, что физическая и метафизическая информация – не одно и то же. Дескать теория информации изучает только цифровые данные, а информация как таковая – это другое. Ведь об информации можно говорить только при наличии источника и приёмника информации, а значит, её объективно не существует без субъекта, который будет её воспринимать и интерпретировать. Кроме того, ни количество информации по Хартли, ни количество энтропии по Шеннону не позволяют оценить смысл сообщения. Но значит ли это, что смысл, глубину или сложность информации нельзя измерить количественно и объективно? Пожалуй, пришло время разобраться, что такое сложность, как её можно измерить, связана ли она с упорядоченностью системы и есть ли у неё объективные критерии. Также мы выясним, насколько наши сообщения универсальны и можно ли прочитать их вне биологического или культурного контекста.
Информация субъективна?
Сторонники эмпиризма, позитивизма и солипсизма считают, что энтропия – мера неопределённости системы для наблюдателя, которая зависит от его знаний. Если наблюдателю уже всё известно о системе или он уже получал такой сигнал, то для него энтропия системы равна нулю, поскольку в сообщении не будет новизны. А для другого наблюдателя этот сигнал может нести много информации, поскольку он получает сообщение впервые.
Действительно, если вы не умеете читать или не знаете русского языка, то данная статья будет для вас бессмысленным набором непонятных символов. Соответственно энтропия каждого следующего бита будет максимальной, избыточности не будет вообще. Если вы умеете читать и знаете язык, но ранее не изучали теорию информации, то вы сможете в некоторой степени предсказать каждую следующую букву и даже слово, как это делает GPT, но в целом изложенная здесь информация будет для вас новой, а значит, энтропия останется высокой, избыточность – низкой. Если вы изучали теорию информации, то для вас в тексте статьи будет мало новизны, соответственно его энтропия будет ниже, а избыточность - выше. Если же вы читаете статью повторно, то она уже хорошо вам знакома и предсказуема, а значит, содержит минимум энтропии и максимум избыточности.
Но ведь физически текст статьи каким был, таким и остался. Ни одна буква в нём не изменилась, а энтропия упала с максимума до нуля. Как же так? А дело в том, что субъективный подход к энтропии не учитывает того, что происходит у вас в голове. Когда вы получаете новую информацию (энтропию), вы формируете новые нейронные связи и тем самым запоминаете какую-то часть этой информации, превращая её в знание. Далее при поступлении новой информации мозг сверяет её с тем, что уже записано в памяти, и на основе этого оценивает энтропию сообщения, т.е. степень его новизны. Когда в памяти будет достаточно нейронных связей, кодирующих теорию информации, любые сообщения по этой теме будут содержать для вас меньше энтропии и больше избыточности. Наконец, если вы выучите статью наизусть, она будет полностью представлена в памяти вашего мозга, и энтропия текста для вас упадёт до нуля.
Конечно, пока мы не умеем объективно оценивать количество информации, записанной в нейросетях мозга. Поэтому единственный способ проверить ваши знания – попросить вас воспроизвести их в устной или письменной форме. Но можно предположить, что запоминание новой информации означает упорядочивание нейронных связей, т.е. снижение их энтропии. Получается, что в процессе обучения снижается энтропия не текста, а вашего мозга. Но если энтропия снизилась в одном месте, она должна вырасти в другом, как того требует второй закон термодинамики. В данном случае мозг избавляется от энтропии вместе с теплом, которо�� выделяется в ходе химических реакций, сопровождающих процесс обработки информации. И рост термодинамической энтропии окружающей среды будет на порядки быстрее, чем снижение информационной энтропии у вас в голове.
Проблема субъективности энтропии решается по аналогии с проблемой измерения в квантовой механике, где исход эксперимента решает не субъект-наблюдатель, а измерительный прибор, которым может быть всё, что угодно (см. статью «Эффект наблюдателя»). Как мы выяснили в предыдущей статье на примере демона Максвелла, информация – это физическая характеристика системы, а устройства её хранения – это физические объекты, они должны быть включены в общее описание системы наряду с другими физическими параметрами. Поэтому принцип Ландауэра в обобщённой формулировке звучит так: «любая информация, имеющая физическое представление, должна каким-то образом быть встроена в статистически-механические степени свободы физической системы». Отсюда следует, что наблюдатель или измерительный прибор становятся частью системы, взаимодействуя с ней или получая о ней информацию.
Когда мы измеряем физическую систему, воспринимаем исходящий от неё сигнал, обрабатываем эти данные мозгом и запоминаем их, мы сами физически изменяемся, подобно демону Максвелла. На клеточном уровне происходит перестройка нейронных связей мозга, а на молекулярном уровне это сопровождается химическими реакциями с участием нейромедиаторов и выделением тепла. С точки зрения наблюдателя энтропия системы, которую он измерил, снизилась, но он тем самым получил новые знания и потратил на это энергию, поэтому общая энтропия системы вместе с наблюдателем и средой увеличилась. Даже если в сообщении нет новизны, нам всё равно нужно обработать его и сравнить с информацией, записанной в памяти, что также увеличивает энтропию.
Информация нефизична?
Ок, с физикой процесса обучения разобрались. Теперь представим такую ситуацию. Доцент кафедры информатики какого-нибудь ВУЗа читает лекцию по теории информации. В аудитории вместе с ним находятся: кот, попугай, школьник, студент и профессор. Все они получат один и тот же сигнал – звуковые волны, передающие сообщение (текст лекции). Но каждый обработает этот сигнал по-своему. Кот услышит звук, но не распознает в нём сообщения и не поймёт ни слова. Попугай услышит, запомнит и может даже воспроизведёт текст лекции слово в слово, но экзамен по теории информации он не сдаст. Школьник поймёт, что это лекция о чём-то сложном, но ему не хватит знаний, чтобы разобраться в теме. Студент – единственный, кто может не только обработать и запомнить информацию, но ещё и понять её, и эта информация будет для него полезной. Профессор тоже обработает сигнал, но для него в сообщении не будет никакой новизны. В итоге каждый слушатель получит свою долю информации в зависимости от уже имеющихся у него знаний, и у лектора своей информации не убудет.
На подобных примерах идеалисты пытаются показать, что информация субъективна, нелокальна и нематериальна. Якобы локально передаётся только сигнал или цифровые данные, а сама информация возникает в голове у получателя, когда он обрабатывает этот сигнал. Но эта информация не возникнет, если получатель определённым образом не настроен на её приём и не знает её значения. Зато, когда он понял значение сигнала, он как бы синхронизировался или срезонировал с его источником. А у отправителя своей информации не убавилось, стало быть, информация не подчиняется закону сохранения. Так и до телепатии можно докатиться. К счастью, решается всё просто, проблема исключительно в терминологии.
Книга, память компьютера и мозг – это физические носители информации. Электромагнитный или звуковой сигнал – тоже носитель информации, способный передавать её на расстоянии в виде сообщения. Сама информация – это набор возможных состояний соответствующих носителей, которыми можно передать значение или смысл сообщения – идею, мысль, знание. Одну и ту же идею можно выразить разными способами, т.е. закодировать на разных языках. Последовательность символов на том или ином языке – это информация, а значение этих символов – это смысл. Чтобы понять смысл, нужно знать язык, на котором он закодирован.
Ладно, - скажут идеалисты, - пусть информация – это физическая величина, реализованная в состояниях её носителя. Но значение или смысл, который в ней содержится – уж точно нематериален, субъективен и неизмерим, разве не так?
Три уровня информации
Дуглас Хофштадтер в своей знаменитой книге «Гёдель, Эшер, Бах – эта бесконечная гирлянда» выделяет три уровня информации: (1) сообщение-рамка; (2) внешнее сообщение; (3) внутреннее сообщение. Понять сообщение-рамку означает признать необходимость декодирующего механизма. Понять внешнее сообщение означает построить — или знать, как построить — правильный декодирующий механизм для внутреннего сообщения. Понять внутреннее сообщение означает извлечь значение, вложенное в сообщение его отправителем. Например, вы находите на берегу моря запечатанную бутылку с запиской. Сообщение-рамка – это сама бутылка с бумагой внутри – носитель информации. Внешнее сообщение – это текст, написанный на каком-то языке – собственно информация. Внутреннее сообщение – это содержание текста – значение, смысл информации. Даже не зная языка и не понимая содержания сообщения, мы можем понять, что бутылка с запиской – носитель информации. «Чтобы отбросить бутылку, не попытавшись ее открыть, понадобилось бы потрясающее — почти нечеловеческое — отсутствие любопытства» - пишет Хофштадтер.
Носители одной и той же информации в той или иной степени изоморфны: звуковая дорожка и звуковые волны, структура генотипа и структура фенотипа, цепочки активирующихся нейронов и возникающие в голове мысли. Однако в случае с музыкой изоморфизм прямой, а в случае с ДНК или нейронами информация распределена по всему носителю и не может быть прочитана напрямую. Проигрыватель, РНК с рибосомами и фМРТ – интепретаторы, осуществляющие изоморфизм физически, переводя информацию с одного носителя на другой. Проигрыватель переводит музыку с пластинки в звуковые волны, РНК с рибосомами переводят генетическую информацию из ДНК в белки, а фМРТ переводит мысли из нейросетей мозга в цифровое изображение. «Слова могут быть символами идей и вещей, и биты тоже. Слово и бит – это средства передачи информации, но чтобы понять смысл и придать им значение, нужен интерпретатор» - пишет Сет Ллойд в книге «Программируя Вселенную».

Философам-номиналистам нравится идея о том, что слова означают лишь то, что мы хотим, чтобы они означали. Часто зависимость смысла от интерпретации выражают с помощью понятия языковых игр, введённого Людвигом Витгенштейном в работе «Философские исследования». Есть принять его идею о том, что значение информации заключается в действии, которое она вызывает, то смысл компьютерной программы заключается в действиях, которые выполняет компьютер, интерпретируя эту программу, смысл ДНК – в синтезируемых по её инструкциям белках, а смысл музыки – в эмоциях, которые она у нас вызывает. А если звуковую дорожку, ДНК или компьютерную программу поместить в другую среду, где нет соответствующего интерпретатора, они окажутся бесполезными и потеряют смысл. Или нет?
Универсальность информации
Насколько наши сообщения универсальны? Можно ли расшифровать их вне нашего культурного или биологического контекста? Или каждый наблюдатель привносит в сообщение своё собственное значение, и без наблюдателя объективного значения у сообщений нет? Присуще ли значение самому сообщению, или же оно всегда порождается взаимодействием разума с этим сообщением?
Есть точка зрения, что сообщение не имеет смысла само по себе без интерпретатора, и что информация бесполезна вне контекста. Это т.н. «теория музыкального автомата»: никакое сообщение не содержит присущего ему значения, поскольку, чтобы понять какое-либо сообщение, его надо сначала ввести в «музыкальный автомат», т.е. информация, содержащаяся в этом автомате должна быть добавлена к сообщению – и только тогда у него появится значение. Но такой подход приводит к бесконечному регрессу: чтобы понять любое сообщение, нам необходимо сообщение, говорящее нам, как понять это сообщение, и т.д. Существует бесконечная иерархия уровней сообщений, которая не позволяет понять ни одного из них. Однако на практике мы всё же понимаем сообщения без дополнительных инструкций. Наш мозг – достаточно сложная физическая система со встроенным механизмом распознавания сообщений – «музыкальным автоматом». Он был настроен эволюцией на распознавание сообщений в звуках и символах так же, как он настроен на распознавание лиц или на распознавание съедобного среди несъедобного. Поэтому дети очень быстро обучаются языку и письменности, а взрослым это даётся с большим трудом.
Противоположная точка зрения говорит о том, что по крайней мере некоторые сообщения содержат универсальный смысл, для раскрытия которого необходим только универсальный интерпретатор – разум. Иначе говоря, носитель информации имеет настолько убедительную внутреннюю логику, что извлечь из нее информацию возможно в любом случае. Будучи сторонником этого подхода, Дуглас Хофштадтер отмечает: «Значение содержится в самом тексте именно потому, что его воздействие на разум предсказуемо. В итоге мы можем утверждать, что значение является частью самого предмета постольку, поскольку этот предмет воздействует на разум определённым предсказуемым способом». «Мы можем приписать все значения (рамку, внешнее и внутреннее) самому сообщению, поскольку сами декодирующие механизмы универсальны — иными словами, они представляют собой универсальные формы природы, возникающие в различных контекстах».
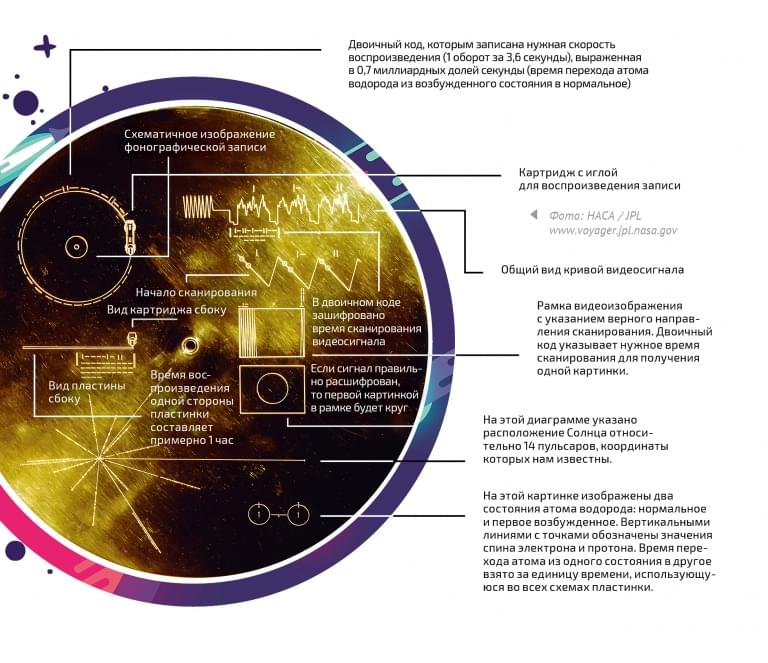
Представьте, что некий внеземной разум получает текстовое сообщение в виде набора символов А, Г, Ц, Т – полный геном человека. Едва ли он сможет по этим символам восстановить фенотип или хотя бы понять, что в них есть какой-то смысл. А если он найдёт молекулу ДНК человека? Молекула ДНК достаточ��о сложная, чтобы любой разум увидел в ней сообщение-рамку. Апериодический кристалл в форме двойной спирали длиной в миллиарды символов, составленный из четырёх оснований – очевидный признак, что здесь что-то не так. Далее инопланетянин мог бы изучить химическую структуру ДНК и подобрать для неё подходящий тип химической среды, чтобы расшифровать язык – генетический код. Наконец, путём длительного перебора всех возможных вариантов среды (для достаточно мощного компьютера это не проблема) можно полностью воссоздать химический контекст, необходимый для расшифровки внутреннего сообщения ДНК – живую клетку. Тогда внеземной разум сможет воспроизвести соответствующую среду на своей экзопланете, вырастить клонированного человека и даже поддерживать жизнь популяции. Конечно, это будет намного сложнее, чем возродить популяцию недавно исчезнувших видов на планете Земля – тех же мамонтов или неандертальцев. Но всё же репликатор потенциально способен побудить к его копированию любую среду. В силу универсальности вычислений любой разум и любой компьютер, независимо от физической реализации, имеет один и тот же набор выполнимых вычислительных задач – репертуар.

Аналогичные критерии сложности применимы и к артефактам человеческой культуры. Здесь Хофштадтер сравнивает две запущенные в космос пластинки – одна с музыкой Баха, вторая с музыкой Джона Кейджа. Разумеется, у инопланетян нет проигрывателей для этих пластинок, а может, нет и органов чувств для распознавания звуковых сигналов. Но глухота не мешала Бетховену писать музыку, и даже слепоглухонемому с рождения человеку можно передать мелодию другим способом – например, подавать электрические импульсы на рецепторы языка. Поэтому любой разум способен прочитать по крайней мере сообщение-рамку, которое сигнализирует о наличии внутреннего значения. Но в пластинке Баха он распознает сложно организованную последовательность знаков, соответствующую сообщению-рамке, а в пластинке Кейджа – неожиданно, случайный шум. А всё потому, что музыка Баха содержит больше смысла, она универсальна и не особо связана с земной культурой. А музыка Кейджа имеет смысл только в культурном контексте постмодерна, она требует от слушателя знания истории западной музыки, и даже при наличии такого знания нельзя быть уверенным, что правильно её понял. В первом случае знание закодировано в самой музыке, во втором случае – в «музыкальном автомате». Так можно ли измерить это знание количественно?
Сложность и упорядоченность
Очевидно, количество информации по Хартли или энтропия по Шеннону не помогут измерить скрытый в информации смысл. Полезная информация, знание или смысл обычно интуитивно соотносятся с понятиями сложности, глубины и упорядоченности, а информационная энтропия по Шеннону измеряет лишь случайность, не имеющую к сложности никакого отношения. Например, различия между живым и мёртвым организмами очевидно, хотя с точки зрения квантовой механики и теории информации количество информации в них одинаково. У строки из нулей шенноновская энтропия ниже, чем у случайной последовательности чисел, но с точки зрения здравого смысла содержания нет ни там, ни там. А сжатое до предела осмысленное сообщение, которое содержит чистую информацию (энтропию), формально неотличимо от шума, т.е. случайной строки битов. Но такое сообщение будет трудноварьируемым и сложным, а сообщение, в котором количество битов информации намного превышает энтропию – легковарьируемым, т.е. содержать много «воды».
Величина, отображающая инвариантность текста, называется избыточностью. Она является необходимым условием, чтобы сообщение читалось. Но это условие необходимо исключительно для интерпретатора информации – мозга или компьютера. Чем сложнее устроен интерпретатор, тем меньше нужно избыточности в сообщении, чтобы он его прочитал. Проще говоря, умный человек понимает с полуслова, а дураку нужно всё долго и подробно объяснять. Однако ни избыточность, ни энтропия по Шеннону никак не отображает закономерности в тексте и степень его упорядоченности. Энтропия текста зависит только от частот символов, но не зависит от их порядка. В случае с незначительными вариациями это не имеет особого значения для понимания, как показывает мемный текст с переставленными буквами в словах: «По рзелульаттам илссеовадний одонго анлигйсокго унвиертисета, не иеемт занчнеия, в кокам пряокде рсапожолены бкувы в солве. Галвоне, чотбы преавя и пслоендяя бквуы блыи на мсете. Осатьлыне бкувы мгоут селдовтаь в плоонм бсепордяке, все-рвано ткест чтаитсея без побрелм. Пичрионй эгото ялвятеся то, что мы чиатем не кдаужю бкуву по отдльенотси, а все солво цликеом». Но если взять целую книгу и беспорядочно перемешать в ней все буквы, или наоборот, рассортировать их по алфавиту, избыточность и энтропия текста по Шеннону не изменятся, а книга станет нечитаемой. Как же измерить именно осмысленность текста, его упорядоченную сложность?
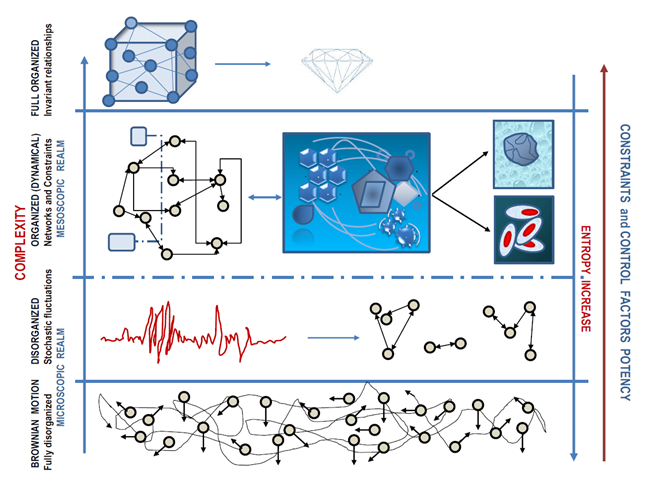
В 1948 г. Уоррен Уивер провёл различие между двумя формами сложности: неупорядоченной и упорядоченной, чтобы формализовать разницу между системами с большим количеством случайных взаимодействий и системами, в которых взаимодействия происходят в рамках определённых закономерностей и связаны с корреляцией между элементами. Явления неупорядоченной сложности рассматриваются с использованием теории вероятностей и статистической механики, в то время как упорядоченная сложность имеет дело с явлениями, которые требуют одновременного рассмотрения значительного числа факторов, взаимосвязанных в единое целое. На бытовом уровне мы говорим о неупорядоченной сложности, когда обозначаем этим словом что-то непонятное, запутанное и хитросплетённое, а об упорядоченной сложности – когда подразумеваем нечто систематизированное, замороченное и тонко настроенное.

Упорядоченная сложность – эмерджентное свойство системы, которые невозможно объяснить посредством анализа отдельных элементов этой системы. Сложность поведения системы может полиномиально или даже экспоненциально превосходить сумму сложностей поведения входящих в систему элементов. Когда мы сжигаем книгу, информации в полученном дыме и горстке пепла не становится меньше, но энт��опия системы возрастает, а значит, упорядоченная сложность переходит в неупорядоченную – полезная информация смешивается с шумом и становится нечитаемой. Упорядоченную сложность и самоорганизацию как свойства сложных адаптивных систем изучают такие междисциплинарные науки, как синергетика, неравновесная термодинамика и теория хаоса. Мы будем разбирать их понятийный аппарат в отдельной статье, а сейчас нас интересует более обобщённое определение сложности в рамках информатики. Понятно, что речь пойдёт о математически менее строгих, чем энтропия в теории информации, но в то же время более универсальных способах измерения.
Меры сложности
Существует много способов измерения сложности. Сет Ллойд в статье «Measures of Complexity: A Nonexhaustive List» насчитал их целых 42. Он разделил эти меры сложности на четыре категории: 1) меры того, насколько сложно что-то описать (алгоритмическая сложность); 2) меры того, насколько сложно что-то сделать (вычислительная сложность); 3) меры степени организации в системе и 4) неколичественные характеристики (например, самоорганизация или сложность адаптивных систем). С полным списком мер сложности вы можете ознакомиться здесь. Рассмотрим некоторые из них.
1. Алгоритмическая, или колмогоровская сложность. Была введена в середине 60-х гг. как основное понятие алгоритмической теории информации, которую независимо друг от друга разрабатывали Рэй Соломонофф, Андрей Колмогоров и Грегори Хайтин. Алгоритмическая сложность строки (текста, числа или просто последовательности битов) равна длине самой короткой компьютерной программы, которая выводит эту строку. Иначе говоря, это мера того, как трудно представить строку с помощью универсального компьютера. Рэй Соломонофф рассматривал алгоритмическую сложность как математический эквивалент бритвы Оккама – философского принципа, призывающего предпочитать простые объяснения явлений сложным. В принципе колмогоровскую сложность можно обобщить как длину самого короткого описания объекта, поскольку программа может быть написана как на машинном, так и на естественном языке, или в виде математической формулы. Тогда эта величина будет применима не только к цифровым данным, но и к физическим системам.

В статье «Информация об информации» мы вычисляли количество информации и энтропию в трёх сообщениях. В случае со строкой из 50-ти битов мы имеем 250 возможных комбинаций. Большинство этих комбинаций будут случайными сообщениями. Сложность такого сообщения максимальна – 50 бит. Но какая-то небольшая часть сообщений (допустим, миллиард) получатся связными: в них можно будет прочитать слова, цифры или команды на каком-нибудь языке программирования. Такие сообщения можно сжать, поэтому алгоритмическая сложность у них будет ниже. Например, возьмём строку из первого миллиона знаков числа пи. Её можно вывести командой «print 3,1415926…» (где «…» состоит из остальных 999992 цифр), но такая программа будет длиннее самой этой строки. А можно составить гораздо более короткую программу из нескольких сотен инструкций, которая самостоятельно вычислит миллион знаков числа пи. Её длина в битах и является колмогоровской сложностью числа пи. Конечно, есть много разных языков программирования, и в каждом из них программа будет иметь свою специфику. Но в силу универсального характера вычислений любые два тьюринг-полных языка могут быть реализованы друг в друге, а значит, программу легко перевести с одного на другой, и её длина при этом сильно не изменится.
Вы, наверно, обратили внимание, что алгоритмическая сложность во многом пересекается с информационной энтропией по Шеннону. И та, и другая величина показывает, до какой степени можно сжать последовательность битов без потери смысла. В чём же между ними разница? В том, что энтропия Шеннона отображает только вероятность появления каждого знака в последовательности, а колмогоровская сложность учитывает все алгоритмические закономерности. Кроме того, колмогоровская сложность измеряет количество информации в конкретных объектах (строках), а не в случайных величинах, как энтропия Шеннона. Математически соотношение колмогоровской сложности и энтропии Шеннона устанавливает теорема Брудно. Например, строка «1, 1, 2, 3, 5, 8, 13…» по формуле Шеннона имеет максимальную энтропию – примерно 7 бит на символ. Но колмогоровская сложность у неё низкая, поскольку это последовательность Фибоначчи, которую можно задать короткой формулой [F(n) = F(n−1) + F(n−2) для n = 3, 4, 5, …, F(1) =1, F(2) = 1]. Если же взять истинно случайную последовательность знаков, то её колмогоровская сложность даже превысит энтропию, причём ровно на столько бит, сколько нужно для записи команды «print». Поэтому случайной строка называется тогда и только тогда, когда она короче любой компьютерной программы, способной её вывести.

Интересно, что функция определения алгоритмической сложности – невычислимая. Узнать алгоритмическую сложность строки можно только приблизительно, потому что никогда нельзя быть уверенным, что именно эта программа – самая короткая. Поиск самой короткой программы является рекурсивным процессом, как и предсказание собственных действий в будущем. Аналогично теорема Гёделя о неполноте не позволяет оценить сложность формальной системы, а проблема остановки Тьюринга не даёт компьютеру вычислить, остановится другой компьютер при выполнении произвольной программы или нет. Ещё один нюанс – строка с высокой алгоритмической сложностью не выглядит сложной в обыденном понимании, скорее она выглядит случайной. Её легко получить с помощью генератора случайных чисел, а по-настоящему сложные вещи обычно воспроизвести трудно. С другой стороны, короткая программа может давать на выходе замысловатый фрактал, который будет выглядеть сложным, несмотря на низкую колмогоровскую сложность.
2. Вычислительная сложность. Теория сложности вычислений изучает ресурсы (время и объём памяти), необходимые абстрактному вычислителю (машине Тьюринга) для решения той или иной задачи, т.е. каким образом можно решать специфические вычислительные и информационные задачи с максимальной эффективностью. В этой теории выделяют различные классы сложности (P, NP, PSPACE, EXPTIME и EXPSPACE), которые можно разделить на две группы: временная и пространственная сложности. Временная сложность равна числу шагов (элементарных логических операций), которые нужно выполнить в ходе вычисления, с учётом размера входных данных. А число битов в памяти компьютера, необходимых для вычисления, называется пространственной вычислительной сложностью. Обе величины отображают не столько сложность объекта, сколько количество ресурсов, которые требуются для его моделирования. Но бывает так, что для создания чего-то сложного нужно приложить совсем немного усилий. Вспомните универсальный алгоритм инженера. И наоборот, вычисление может занимать много времени и расходовать много энергии, но не производить ничего сложного – например, майнинг криптовалюты.
3. Логическая глубина. Величина, предложенная в 1988 г. Чарльзом Беннеттом в качестве компромисса между алгоритмической сложностью (мерой содержания информации) и вычислительной сложностью (мерой необходимых усилий). Она подсчитывает вычислительные ресурсы, которые требуются для получения строки битов из её самого вероятного описания, то есть из самой короткой программы, выводящей данную строку. В отличие от сложности по Колмогорову, логическая глубина учитывает время вычисления алгоритма почти минимальной длины, а не длину минимального алгоритма. Здесь уже прослеживается важная закономерность. Простая строка вроде последовательности из миллиона единиц, созданная короткой и быстро выполняемой программой, логически неглубока. Алгоритмически сложная строка из случайной последовательности битов, созданная длинной, но быстро выполняемой программой (например, «print…»), тоже логически неглубока. А вот строка из первого миллиона знаков числа пи обладает высокой логической глубиной, потому что даже самая короткая программа будет вычислять её долго.
4. Термодинамическая глубина. Обобщение логической глубины на все физические системы, предложенное в конце 80-х гг. Хайнцем Пэджелсом и Сетом Ллойдом. Для её вычисления нужно знать самый вероятный способ создания физической системы (аналог колмогоровской сложности) и объём физических ресурсов, необходимых для её создания (аналог вычислительной сложности). Термодинамическая глубина равна количеству полезной информации (негэнтропии), то есть числу битов полезной эне��гии и массы, затраченных на создание физической системы. Например, у кристаллов льда или молекул водяного пара термодинамическая глубина невелика, поскольку создать эти системы довольно просто, несмотря на то, что энтропия пара гораздо выше энтропии льда. Зато для создания живой клетки нужно осуществить огромное количество операций на протяжении миллиардов лет, поэтому у неё термодинамическая глубина будет высокой даже при небольшой энтропии.
Тесная связь логической и термодинамической глубины явно прослеживается в работе квантового компьютера. Термодинамическая глубина созданной им строки битов равна пространственной вычислительной сложности самой короткой программы, то есть объёму памяти в кубитах, задействованному для получения этой строки. А физическим аналогом временной вычислительной сложности (числа операций, необходимых для выведения строки) является число операций над кубитами (сильных или слабых измерений), произведенных для создания физической системы, что равно её действию, делённому на постоянную Планка.
5. Эффективная сложность. Последняя в нашем списке величина, введённая в 1996 г. известным физиком Мюрреем Гелл-Манном и Сетом Ллойдом, измеряет степень регулярности системы. Это часть от общего количества информации в физической системе, необходимая для описания регулярных аспектов этой системы, в противоположность энтропии, описывающей её случайные аспекты. Здесь учитываются «полезные» биты, инверсия которых нарушает целостность или функционирование системы, и «бесполезные», инверсия которых ни на что не влияет. То есть эффективная сложность – мера полезности информации. Сет Ллойд пишет, что «значимость бита зависит не только от его значения, но и от того, как это значение с течением времени влияет на другие биты, будучи частью процесса постоянной обработки информации, который и составляет динамическую эволюцию Вселенной». Давайте разберём этот подход подробнее.

Эффективная сложность как мера значимости информации
Вспомним о термодинамической энтропии Больцмана-Гиббса, которую мы рассматривали в статье «Правда и мифы об энтропии». Представьте себе самолёт в рабочем состоянии и его же, разобранного на запчасти. Число атомов и там, и там одинаковое. Но рабочий самолёт можно получить только одним способом, соединив детали в определённой последовательности. Незначительные перестановки деталей приведут к тому, что он уже не сможет взлететь, но сохранит узнаваемую форму. Более существенные перестановки превратят самолёт в кучу запчастей. Ещё более значительные перестановки на микроскопическом уровне сделают из запчастей просто кучу атомов. Случайным образом перемешивая эти атомы, мы вряд ли соберём из них хотя бы одну запчасть, не говоря уже о целом самолёте. Потому что существует намного больше способов расположить атомы в виде кучи металлолома, чем в виде функционирующего самолёта. Энтропия по Больцману – это логарифм числа вариантов расположения атомов или молекул, которыми можно получить данную макроскопическую систему. Мы выяснили, что у самолёта энтропия низкая, а у кучи металлолома – высокая. Это объективная характеристика системы, не зависящая от точки зрения.
Аналогично можно рассуждать и об информации в физической системе. Здесь нельзя не вспомнить венгерского математика Абрахама Вальда, который во время Второй мировой войны решал задачу уменьшения потерь американских бомбардировщиков. На первый взгляд кажется, что укреплять бронёй нужно те части самолётов, на которых обнаружено больше всего повреждений от вражеского огня: фюзеляж и крылья. Однако исследование Вальда показало, что на самом деле попадания от вражеского огня распределяются равномерно, но те самолёты, которые получили повреждения двигателей или топливного бака, попросту не возвращаются на базу. Следовательно, нужно укреплять те места, которые у вернувшихся самолётов самые целые. Эту историю обычно упоминают в качестве иллюстрации ошибки выжившего, когда мы находим общие черты у «выживших», не включая в статистику «погибших». Но нас интересует другое. Биты информации, кодирующие устройство двигателя самолёта, топливной системы или органов управления, важнее таких же битов, кодирующих расположение атомов металла в крыле или фюзеляже. Потому что первые при инверсии сделают самолёт нефункциональным, а инверсия вторых никак не отразится на его состоянии.

Получается, что не все биты равнозначны. Количество информации может быть одинаковым, а её значимость – разной. Значимость ответа «да» или «нет» зависит от заданного вопроса. Как же определить значимость информации? На первый взгляд, она субъективна и не поддаётся строгому математическому описанию. Но если подумать, здесь всё зависит от того, как обрабатывается информация и в каком контексте, а не от того, кем она обрабатывается: человеком, компьютером, клеткой или атомами. Значимость бита пропорциональна тому, как он с течением времени влияет на другие биты и какое место занимает в макроскопической системе. Функциональность, эффективность и целостность системы – её эмерджентные свойства, являются объективными критериями важности информации.
Итак, в технической системе критерием значимости битов является способность системы выполнять свои функции. В природе таким критерием является энергоэффективность системы – насколько хорошо она использует свободную энергию и преобразует её в тепло, в том числе путём саморепликации. Сет Ллойд определил эффективную сложность живой системы как число битов информации, влияющих на способность этой системы потреблять энергию и воспроизводить себя вариативно. К этой формуле мы ещё вернёмся, когда будем говорить о происхождении жизни. А пока отметим, что эффективная сложность – это контрфактическая величина, для вычисления которой нужно рассматривать не только саму систему, но и все её возможные вариации. Контрфактический подход мы уже упоминали в статье «Теория конструкторов»: количество информации в системе связано с возможностью или невозможностью определённых преобразований, а именно – логических операций «инверсия» и «копирование».
Эволюция сложности в биоинформатике
Возьмём двойную спираль ДНК. Она выглядит как случайная последовательность из четырёх букв – нуклеотидов А, Г, Ц и Т. Кодирующие участки – гены – формально неотличимы от некодирующей «мусорной» части генома. Но информация ДНК состоит из «полезных» битов генетического кода, определяющих способность организма выживать и размножаться, и «бесполезных» или «мусорных» битов, не играющих никакой роли в судьбе особи. В процессе обработки (транскрипции) этой информации гены читаются как команды и вызывают синтез определённых белков из аминокислот, а некодирующие участки игнорируются и в лучшем случае служат «буфером», защищающим от мутаций. Если начать случайно переставлять или заменять буквы в геноме, что и происходит в природе в ходе мутаций, обнаружится чёткая закономерность. Малейшие изменения в генах будут отражаться на фенотипе их носителей, и подавляющее большинство этих вариаций окажутся для них фатальными. А изменения в «мусорной» части никак не отразятся на выживаемости носителей. Если среда остаётся постоянной, т.е. действует стабилизирующий отбор, по итогу мы получим популяцию с более-менее одинаковыми генами и совершенно разными «мусорными» участками ДНК.

Для простоты и наглядности допустим, что в нашем генетическом коде всего две буквы – 0 и 1, а сам геном состоит из четырёх нуклеотидов. Составляем полный список комбинаций из двух по четыре – 16 геномов. Это наши особи. Далее мы помещаем их в некую среду, которая будет способствовать выживанию определённых «генов» и отсеивать нежизнеспособные комбинации. Большинство особей вымирают сразу, некоторые доходят до середины, но проигрывают в конкуренции с более адаптированными соперниками, и в конечном итоге у нас остаются четыре комбинации. Все они начинаются с двух единиц, а значит, две единицы в первой половине генома являются «генами», обеспечивающими максимальную адаптацию к среде и прошедшими отбор. Но во второй половине генома встречаются все четыре возможных комбинации 0 и 1, следовательно, это «мусорная» часть генома, никак не влияющая на адаптацию особи. Так выглядит эволюция с точки зрения мультивселенной. А что делать, если мы ничего не знаем об альтернативных комбинациях, а имеем только один геном, скажем, 1101? Можно смоделировать на компьютере эволюцию всех возможных комбинаций, как в нашем примере, но в случае с реальной ДНК это потребует колоссальных вычислительных ресурсов. Или можно по очереди инвертировать каждый бит и смотреть, влияет это на адаптацию или нет. Тогда достаточно будет перебрать всего 4 комбинации из 16-ти возможных. И мы сможем сказать, что первые два бита являются эффективно сложными, а вторые два – «мусорными».
Теперь представьте список всех возможных комбинаций нуклеотидов человеческой ДНК – порядка 46200000000 строк. Каждой из них соответствует смоделированная особь (это не обязательно получится именно человек), помещённая в типичную для нашего вида среду, которая не меняется. Запускаем симуляцию естественного отбора в одном поколении и без мутаций, чтобы ДНК не повторялись. Абсолютное большинство особей окажутся нежизнеспособными и погибнут в самом начале отбора. Оставшиеся носители похожих генов или вариантов одних и тех же генов будут конкурировать за ресурсы. Генетическое разнообразие будет постепенно сокращаться, пока не останутся самые устойчивые комбинации генов, кодирующие самые полезные в данной среде адаптации. Для каждой удачной комбинации выживет ровно столько её носителей, сколько существует возможных комбинаций «мусорной» части генома. А для каждой «мусорной» комбинации останется только небольшое число носителей удачных комбинаций генов, остальные до конца эксперимента не доживут. Значит, мы получим много особей с одинаковыми генами и мало особей с одинаковыми «мусорными» участками ДНК, плюс огромное количество «вымерших» ветвей. Следовательно, гены содержат в себе эффективную сложность или знание.
Вывод
выделяют три уровня информации: сообщение-рамка (физический носитель информации), внешнее сообщение (собственно информация как последовательность символов на некоем языке) и внутреннее сообщение (содержание, значение, смысл информации);
субъективные подходы к измерению информации и энтропии – пережиток эмпиризма и позитивизма;
сложность информации – объективная характеристика, которая определяется способом обработки этой информации;
ни один из 42-х известных науке видов сложности не зависит от субъекта, оценивающего систему, а зависит только от эмерджентных свойств системы;
алгоритмическая или колмогоровская сложность – длина самого короткого описания объекта;
вычислительная сложность, логическая и термодинамическая глубина измеряют ресурсы, необходимые для моделирования объекта;
эффективная сложность – мера полезности или значимости битов информации для системы;
эффективная сложность является контрфактической величиной, для вычисления которой необходимо учитывать не только актуальное, но и возможные состояния рассматриваемой системы;
эффективно сложные, насыщенные смыслом сообщения наиболее универсальны (читаются вне контекста) и обладают таким свойством, как трудноварьируемость. «Убери хоть одну ноту — музыка исчезнет. Измени одну фразу — здание рухнет» - так описывал музыку Моцарта Питер Шеффер в своей пьесе «Амадей» (1979).