Хабр, привет! В этой статье хочу поделиться с вами одной изящной задачей из нашего прошедшего квеста, которая, как мне кажется, заслуживает вашего внимания.
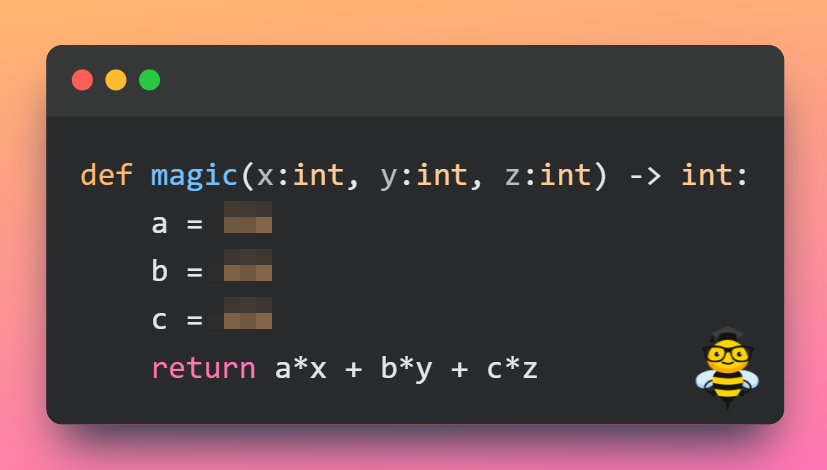
Имеется функция magic(), принимающая три целочисленных аргумента, в теле которой определены константы a, b, c, являющиеся натуральными числами. Требуется определить значения констант a, b и c за минимальное количество вызовов данной функции.
Три вызова функции и система уравнений
Первое, что может прийти в голову при виде такой задачи — это составление системы линейных уравнений:
вызывая функцию с аргументами
x = 1, y = 1, z = 1, мы получим значение выраженияa + b + cвызывая функцию с аргументами
x = 1, y = -1, z = 1, мы получим значение выраженияa - b + cвызывая функцию с аргументами
x = 1, y = 1, z = -1, мы получим значение выраженияa + b - c
Итого мы имеем систему трех линейных уравнений с тремя неизвестными a, b, c. Такая система имеет единственное решение, и его можно найти различными способами, например, методом подстановки.
Три вызова функции без системы уравнений
Поскольку по условию задачи аргументами функции magic() являются целые числа, то мы можем использовать значение 0. Это позволит нам избавиться от ненужных вычислений и сразу найти значения констант a, b и c:
вызывая функцию с аргументами
x = 1, y = 0, z = 0, мы получим значение константыaвызывая функцию с аргументами
x = 0, y = 1, z = 0, мы получим значение константыbвызывая функцию с аргументами
x = 0, y = 0, z = 1, мы получим значение константыc
Получили достаточно красивое решение: компактное и с минимумом вычислений. Однако и такое решение использует три вызова функции magic().
Можно ли сократить количество вызовов функции? Возможно ли решить задачу всего за два вызова функции magic()? Оказывается, можно — при условии, что константы a, b и c являются натуральными числами.
Напомним, что натуральные числа — это целые положительные числа, то есть числа 1, 2, 3, 4 и т. д. Множество натуральных чисел неограниченно сверху.
Два вызова функции
Возьмем произвольное число 8956734. Такое число можно разложить по степеням десяти (base = 10) в виде:
С таким же успехом мы можем разложить данное число по степеням ста (base = 100):
или даже по степеням тысячи (base = 1000):
Почему такое разложение работает? В первом случае число 10 больше, чем любая из цифр от 0 до 9, поэтому в сумме справа нигде не происходит наложения разрядов. Во втором случае число 100 больше, чем любое двухзначное число от 10 до 99. В третьем случае число 1000 больше, чем любое трехзначное число от 100 до 999.
Прежде чем переходить к самому решению, давайте вспомним, как мы можем посчитать количество цифр в произвольном натуральном числе. Для этого нам потребуется использовать десятичный логарифм (можно использовать и конвертацию в строку с последующим вызовом функции len(), но через логарифм получается интереснее).
Приведенный ниже код:
from math import log10
for num in [1, 13, 456, 1673, 56789, 258964, 1234567]:
digit_len = int(log10(num)) + 1
print(digit_len, 10**digit_len)выводит:
1 10
2 100
3 1000
4 10000
5 100000
6 1000000
7 10000000А теперь, собственно, решение задачи. 🔥
Делаем первый вызов функции magic() с аргументами x = 1, y = 1, z = 1, получаем значение суммы a + b + c, которое запишем в переменную total. Такое число total заведомо больше, чем каждое из чисел a, b и c. С помощью десятичного логарифма находим минимальную степень десяти, превышающую число total, которую запишем в переменную power.
Делаем второй вызов функции magic() с аргументами x = power**2, y = power, z = 1. В результате такого вызова мы получим число, которое и будет содержать все три константы a, b, c слева направо. Далее с помощью операторов // (целочисленное деление) и % (нахождение остатка) находим значения констант a, b, c по отдельности:
from math import log10
total = magic(1, 1, 1) # первый вызов функции
power = 10**(int(log10(total)) + 1)
numbers = magic(power**2, power, 1) # второй вызов функции
a, b, c = numbers // power**2, numbers % power**2 // power, numbers % power
print(a, b, c) Рассмотрим пример. Пусть функция magic() имеет вид:

Получаем:
total = 23 + 46 + 19 = 88
power = 10**2 = 100
numbers = 23*100**2 + 46*100 + 19 = 234619
a = 234619 // 100**2 = 23
b = 234619 % 100**2 // 100 = 46
c = 234619 % 100 = 19 Еще один пример. Пусть константы a, b и c состоят из разного количества цифр и функция magic() имеет вид:

Получаем:
total = 19567 + 4 + 231 = 19802
power = 10**5 = 100000
numbers = 19567*100000**2 + 4*100000 + 231 = 195670000400231
a = 195670000400231 // 100000**2 = 19567
b = 195670000400231 % 100000**2 // 100000 = 4
c = 195670000400231 % 100000 = 231Обратите внимание: в числе numbers могут быть "лишние" нули, но это нестрашно. В момент нахождения самих констант a, b и c незначащие ведущие нули пропадут.
Обобщения на большое количество неизвестных
Приведенное решение особенно красиво тем, что его можно масштабировать на любое количество неизвестных констант. В исходной задаче их всего три, но их может быть и больше, скажем, 5 или 10. Единственное, что надо будет поменять, так это код, извлекающий значения констант из итогового числа numbers: его легко обобщить и переписать в виде цикла while.
Рассмотрим пример функции magic() с пятью константами:

Приведенный ниже код:
from math import log10
total = magic(1, 1, 1, 1, 1) # первый вызов функции
power = 10**(int(log10(total)) + 1)
numbers = magic(power**4, power**3, power**2, power, 1) # второй вызов функции
constants = []
while numbers != 0:
constants.append(numbers % power)
numbers //= power
a, b, c, d, e = reversed(constants)
print(a, b, c, d, e)выводит значения всех пяти констант:
314 271828 668 12 7652Напоследок
В разобранном решении задачи с двумя вызовами функции magic() использовались степени десятки (base = 10) в качестве основания системы счисления. Обязательно ли их использовать? На самом деле нет! Мы сделали это исключительно для того, чтобы нам было чуток нагляднее, ведь мы привыкли иметь дело с десятичной системой счисления. В качестве основания системы счисления мы можем использовать значение total, равное сумме констант a, b и c, ведь оно заведомо больше, чем каждое из чисел a, b и c.
total = magic(1, 1, 1) # первый вызов функции
numbers = magic(total**2, total, 1) # второй вызов функции
a, b, c = numbers // total**2, numbers % total**2 // total, numbers % total
print(a, b, c) Пусть функция magic() имеет вид:

Получаем:
total = 432 + 4 + 67 = 503
numbers = 432*503**2 + 4*503 + 67 = 109301967
a = 109301967 // 503**2 = 432
b = 109301967 % 503**2 // 503 = 4
c = 109301967 % 503 = 67Напишите в комментариях, понравилась ли вам задача? Возможно, у вас есть другое решение, которое тоже использует всего два вызова функции. Поделитесь им! А может быть, вам удалось придумать решение задачи всего за один вызов? Делитесь им тоже!
Разбор остальных задач квеста будет опубликован чуть позже.
Присоединяйтесь к нашему телеграм-каналу, будет интересно и познавательно! 🐍