О трехмерном Z-order замолвите слово

«Давным-давно, кажется, в прошлую пятницу» автору попалась на глаза статья, в которой сравниваются разные популярные методы индексации небесных объектов. По причине неровного дыхания к этой теме пришлось разбираться в тонкостях и делать выводы.

Вы спросите: «Кому вообще интересны эти небесные объекты?» и даже: «Ну и при чём здесь 2ГИС?» и будете отчасти правы. Ведь методы пространственного индексирования являются универсальной ценностью.

Обычно, имея дело с геоданными, мы работаем с локальной проекцией на плоскость и тем самым отмахиваемся от искажений. В масштабах планеты это сделать труднее — начинают выпирать астрономические проблемы.
Что касается объёмов данных, уже сейчас в OSM более 4 млрд точек и 300 млн дорог. Это соизмеримо с масштабами, характерными для звёздных объектов. Да и помимо всего прочего, звёздные атласы — отличный стенд для разработки и отладки пространственных алгоритмов.

Обещанные тонкости и выводы под катом.

Прелюдия

Проблемы индексации небесных объектов — это борьба с полярными координатами.
Так как объекты традиционно имеют координаты RA/DEC (широта/долгота), длина градуса долготы зависит от широты, а на полюсах возникают сингулярности. Поэтому при поиске в окрестностях некоторой точки приходится при построении поискового экстента учитывать широту этой точки. А хотелось бы спрятать эти подробности внутрь индекса.
В случае пространственного join’а опять же хочется не нагружать процессор SQL разными интимными подробностями.

Итак, основные внешние требования к методу индексирования («пикселизации») небесных объектов таковы:

1. Иерархическая структура.
2. Равные площади. Имеется ввиду, что площадь под «элементарным пикселем» не должна (в идеале) зависеть от широты и долготы.
3. Изоширотное распределение данных. Хороший метод индексирования приводит к тому, что на любой широте на «элементарный пиксель» в среднем приходится одинаковое количество объектов. Для геообъектов это не так, кстати.

Конечно, использование СУБД накладывает свои ограничения: номер «пикселя» должен легко вычисляться, индекс должен быть компактным, поисковый запрос должен порождать умеренное количество подзапросов.

Известно довольно много сферических многогранников, смежные методы (HEALPix, HTM). Можно, кроме того, предпринять мощение сферы таким вот (или аналогичным) методом:

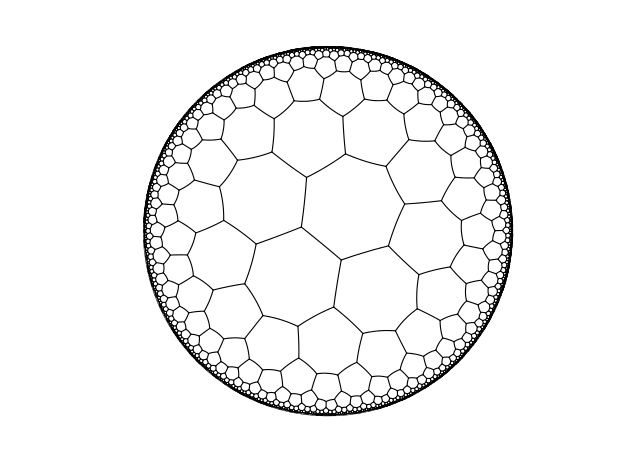
(Правильный семиугольный паркет порядка 3 в модели Пуанкаре на диске)
Но тот, кто придумает для этого варианта дешёвый способ переводить координаты в номер пикселя и получать набор пикселей по конусу, рискует вызвать дьявола.

Приступим

В упомянутой статье сравниваются различные популярные методы индексации, реализованные в Postgres.

1. HAVERSINE — индексируется поле DEC (declination, долгота), потом данные фильтруются;
2. UNIT VECTOR — индексируется поле DEC, при фильтрации вычисляется скалярное произведение вектора тестируемой точки и оси конуса запроса. Косинус отклонения должен быть не меньше заданного (конусом запроса);
   
3. POSTGIS — r-дерево в координатах RA (right ascension, широта)/DEC;
4. Q3C —
   
   • при индексации
     
     1. точки проецируются на грани куба,
     2. номер грани попадает в старшие биты (3 бита для 6 граней) значения индекса,
     3. младшие биты кодируются с помощью Z-order, в который превращаются координаты на грани,
     4. для 32-битного значения максимальный уровень глубины — 14 (14*2+3 = 31). Для 64-битного значения доступна глубина 30, но фактически 16 (см. константу Q3C_INTERLEAVED_NBITS),
        
     5. вычисленные значения помещаются в обычное B-дерево;
   • при поиске
     
     1. конус запроса проецируется на грани губа и образует эллипс,
     2. в худшем случае (угол) это могут быть три эллипса и три подзапроса,
     3. эллипс растеризуется на решётке грани, в результате получается список накрытых им пикселей,
     4. пиксели переводятся в Z-order и таким образом получается список интервалов индекса, потенциально содержащих нужные данные,
     5. далее происходит поиск по индексу и (возможно) более тонкая фильтрация;
   • плюсы
     
     1. простота
     2. штатный компактный индекс,
     3. относительно небольшая неравноценность площадей пикселей,
     4. высокая скорость поиска на небольших запросах;
   • минусы
     
     1. это всё же блочный индекс. Максимальная глубина индекса в 16 бит + 2 бит на 4 грани по экватору. В 2MASS разрешающая способность телескопа — доли угловых секунд, пусть 0.5. Имеем 2*60*60*360 = ~2**21,
     2. индекс предназначен для небольших запросов. В противном случае эллипс накроет большое количество интервалов индекса и это станет проблемой, ведь в этот момент мы не знаем, какие из них не пусты, проверить придется все. Впрочем, это не проблема Z-order’а, индекс со строчной развёрткой вёл бы себя ничуть не лучше. Эта проблема вызвана тем, что мы снаружи понятия не имеем, как фактически устроено (заполнено) дерево. С другой стороны, этот недостаток компенсируется блочностью индекса, возможно, проблематичные по размеру запросы редко возникают в астрономии,
     3. два описанных момента балансируют друг друга. Мы не можем просто так взять и увеличить разрешающую способность индекса, так как произойдёт взрыв числа интервалов. И уменьшить её не можем, так как возрастёт нагрузка на постфильтрацию из-за грубости пикселей;
5. PGSPHERE — точки помещаются на сферу единичного радиуса и их трёхмерные координаты индексируются в r-дереве.
   
   • плюсы
     
     1. отличная идея,
     2. точный индекс, ему не требуется постфильтрация,
     3. штатный для СУБД индекс;
   • минусы
     
     1. r-дерево довольно «толстое», оценка: в 4 раза,
     2. а, следовательно, эффективность кэша страниц падает,
     3. поведение r-дерева сильно зависит от эвристики расщепления страниц, для таких специфических данных было бы хорошо подобрать оптимальную эвристику,
     4. в зависимости от выбранной эвристики r-дерево может начать деградировать если данные интенсивно меняются, для B-дерева, кстати, такая деградация не наступает.

Собственно, результаты

Детали сравнения:

• первые 2 колонки — поиск (первый и последующие) в датасете HEASARC (36,000,000 строк) с точностью 1 градус, использовались серии из 162 искомых точек;
• 3 и 4 колонки — пространственный join (с радиусом 0.01 градуса) между Swift (76,301 строка) и XMM (2,880,728 строк), первый и последующие прогоны.

Относительные результаты таковы:

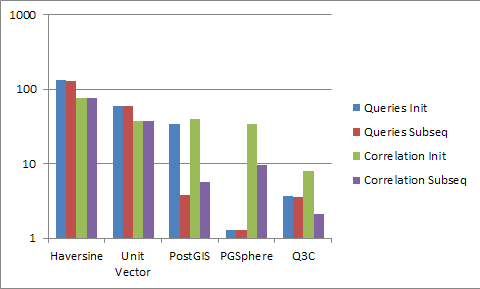
На что следует обратить внимание?

1. PGSphere намного опережает все остальные методы в поиске. Потенциально Q3C мог бы быть быстрее PGSphere, но, по-видимому, на запросах радиусом в 1 градус уже начинают проявляться недостатки высокоуровневой работы с Z-order, число подинтервалов слишком велико.
2. PGSphere быстрее PostGIS, хотя используется более сложное трёхмерное дерево. Объяснить это можно борьбой с искажениями у полюсов, которые не дают использовать индекс на полную мощь.
3. PGSphere медленнее Q3C в пространственном join’е вдвое. Какие будут объяснения?
   
   1. Пространственный join — серия поисков с небольшими радиусами, где поисковые запросы берутся из ведущей таблицы (Swift) и выполняются на ведомой (XMM).
   2. При этом радиус запроса существенно меньше — 0,01 градуса. На таком радиусе сохраняются все преимущества Z-order и ещё не проявляются его недостатки.
   3. Замедление PGSphere, скорее всего, вызвано менее эффективной работой страничного кэша.
4. Q3C минимум вдвое быстрее PostGIS.

Самое время задать вопрос из разряда «а что, если...».

А что, если?

Если сделать гибрид PGSphere и Q3C, где вместо R-дерева используется трёхмерный низкоуровневый Z-order. Почему Z-order, что в нём хорошего? Как минимум, такой метод индексации автоматически удовлетворяет трём первичным внешним требованиям, которые сформулированы в начале статьи. Есть и «внутренние» плюсы.

Z-order

Один из самых известных примеров самоподобной кривой, заметающей квадрат, является Гильбертова кривая. Другой, чуть менее известный пример — z-order.
Наш порядок обхода несколько отличается от канонического, но это не принципиально.
Всякой паре x-битных чисел (x,y) ставится в соответствие 2x-битный z по следующему простому правилу. Биты чисел x, y соединяются в одно число, просто чередуясь друг с другом. При этом биты числа x занимают чётные позиции (если начинать отсчёт с 0), а биты числа y — нечётные.

Для квадрата 64х64 это выглядит так:

Z-order очень удобен для индексации, так как может быть реализован как обычное B-дерево с целочисленным ключом. Однако есть проблемы с эффективным поиском по нему.

Синий прямоугольник на картинке — поисковый запрос. Каждый раз, когда он пересекает кривую, порождается (или заканчивается) непрерывный интервал значений ключей.
Следовательно, если мы каждый такой интервал будем обрабатывать отдельным подзапросом, получим значительные накладные расходы, так как немалая часть этих интервалов пусты, а каждый подзапрос — это проход по дереву индекса.

Если же искать в одном интервале от начала до конца экстента, это равносильно тому, как если бы мы проиндексировали одну только Y-координату и фильтровали по ней.ля запроса в 1/10 от экстента слоя по x&y (1/100 слоя) будет просмотрена 1/10 индекса — КПД 10%, для запроса в 1/100 экстента слоя по x&y (1/10000 слоя) будет просмотрена 1/100 индекса — КПД 1%.

Этим и объясняется, почему данный метод редко используют в СУБД. Вот и в Q3C он в блочном варианте. Хотя самоподобие наделяет его чудесной особенностью — адаптацией к неравномерно распределённым данным. Кроме того, непрерывные отрезки кривой могут накрывать значительные области пространства, что полезно, если суметь этим воспользоваться.
Эффективный (но весьма низкоуровневый) способ работы с Z-order есть, но об этом, возможно, позже. Способ этот распространяется и на трёхмерный индекс.

Впрочем, поведение Z-order в трёхмерном пространстве слабо изучено и требует тщательной проверки. Чем мы и займёмся.

Z-order в 3D

Что мы хотим увидеть?
Как вообще оценить критерий пригодности способа индексации для обработки пространственных данных?

Как уже говорилось, что бы мы ни делали, файл индекса на физическом носителе (нумерация страниц) одномерен, и расположить дву(много)мерные данные без разрывов невозможно.
Самоподобные кривые дают нам возможность минимально соблюсти локальность ссылок, то есть пространственно близкие объекты и на диске будут чаще находиться рядом. Самой приятной в этом отношении является кривая Гильберта, но она дорога с вычислительной точки зрения. Z-order как раз является компромиссом между требованиями к вычислительной простоте и локальности данных.
Но всё же сплошь и рядом близкие точки будут оказываться далеко друг от друга. Как же оценить степень «несовершенства» индексации?

Во-первых, будем исходить из того, что пространственный индекс расположен на страницах дерева. И если две точки попали на одну страницу, значит они физически близки, даже если соответствующие им Z-значения сильно отличаются.
Во-вторых, пространственный поиск осуществляется в некотором экстенте, следовательно, чем меньшее число страниц попало в этот экстент, тем выше скорость обработки запроса.
В-третьих, если поисковый запрос меньше характерного размера страницы, индекс тем «качественней», чем больше вероятность, что поиск ограничится одной страницей.

Итак, можно сформулировать общее правило:
«хороший» метод индексации минимизирует суммарный периметр страниц индекса.
Стоило бы придумать формальный критерий оценки качества, но иногда лучше один раз увидеть всё глазами, чем жонглировать цифрами. А получив общее понимание ситуации можно заняться и формализацией.

Численный эксперимент

Функция вычисления значения индекса:

uint32_t key3ToBits[8] = { 
	0,		1,		1 << 3,			1 | (1<<3),
	(1 << 6),	(1 << 6) | 1,	(1 << 6) | (1 << 3),	1 | (1 << 3) | (1 << 6),
};
uint64_t xy2zv(uint32_t x, uint32_t y, uint32_t z)
{
	uint64_t ret = 0;
	for (int i = 0; i < 7; i++)
	{
		uint64_t tmp = (key3ToBits[x & 7] << 2) | 
				(key3ToBits[y & 7] << 1) | 
				(key3ToBits[z & 7]);
		ret |= tmp << (i * 9);
		x >>= 3; y >>= 3; z >>= 3;
	}
	return ret;
}

Для того чтобы разместиться в 64 битах, мы допускаем для исходных координат разрешение в 21 бит.

Для первой серии нанесём на верхнюю полусферу единичного радиуса точки с шагом в полградуса по широте и долготе.
Центральная часть полусферы выглядит так (в порядке генерации, команда gnuplot: ‘splot ‘data’ w l;’):


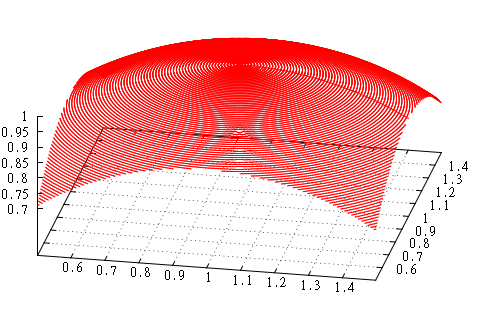
Теперь мы построим Z-значения для каждой точки и отсортируем в соответствии с этими значениями. Значения посажены на решётку в интервалах 0...2 000 000 (т.е. 21 бит). Для контроля будем строить также картину для 2-мерного z-order (только x&y, без z).

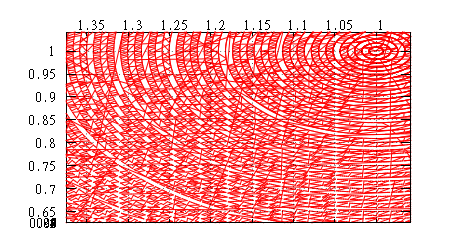
Фрагмент 3d, общий вид обхода сверху. Кроме «прострелов» (от переходов через степень 2-ки) по x&y видны также кольцевые «прострелы» по z.


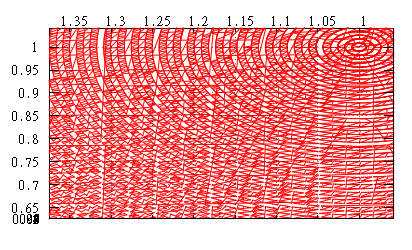
То же для 2d.

Теперь будем симулировать распределение данных по страницам на диске. Предположим, что на страницу попадает 1000 элементов. Тогда первые 1000 элементов в отсортированном массиве попадут на первую страницу и т.д. Для наглядности представлен обход страницы, но он не важен – как мы уже выяснили, важен периметр.

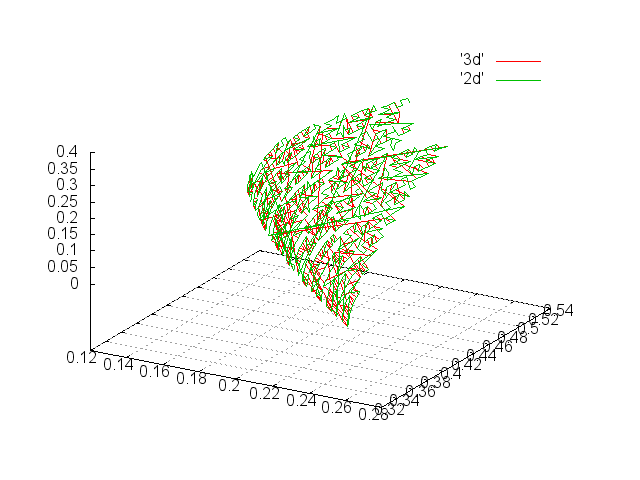Первые 1000 значений.

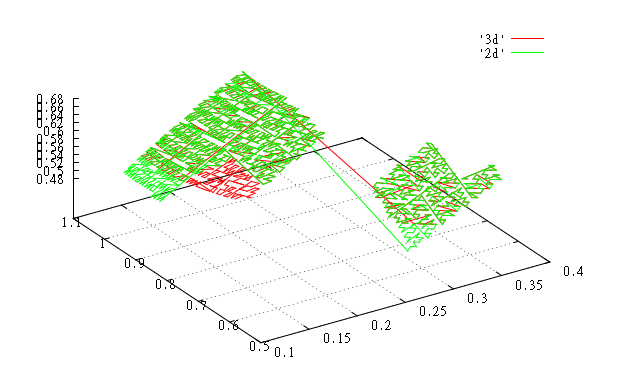Значения с 9000 по 10000.

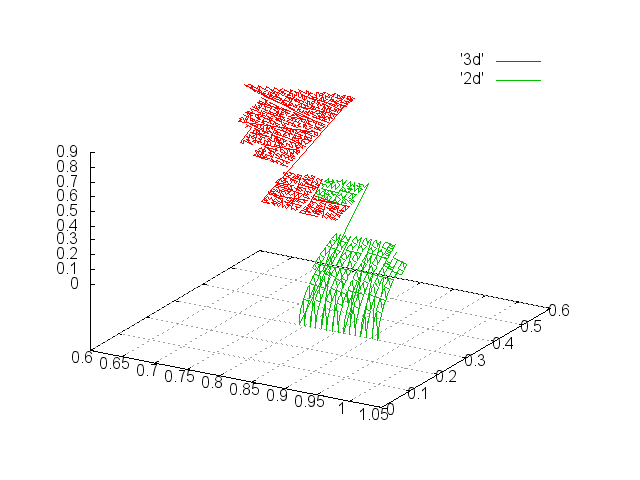Значения с 19000 по 20000.

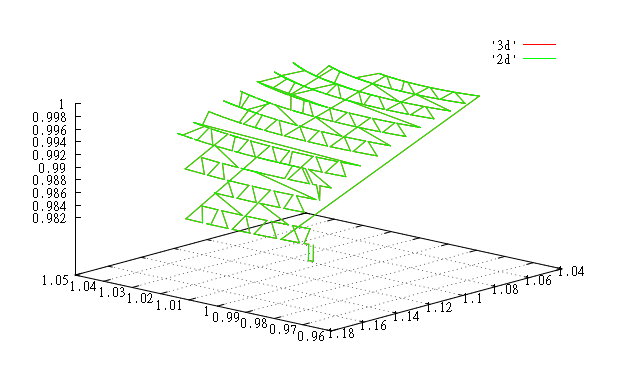Значения с 60000 по 61000. Поскольку сфера в этом месте практически выположилась, 2d и 3d совпадают.

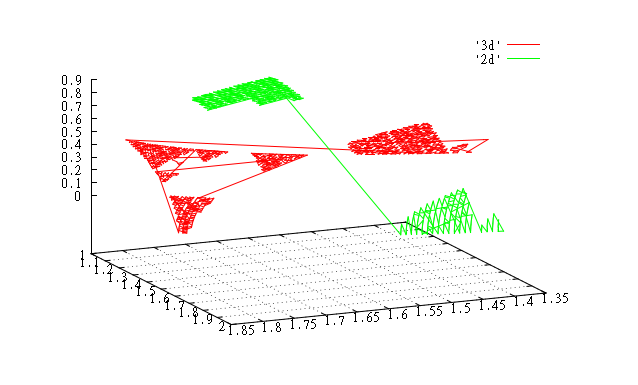Значения с 120000 по 121000. Попали на узел.

Теперь приготовим 150 000 случайных точек на сфере и проделаем всё то же с ними.
Общий вид на обход сверху теперь такой:

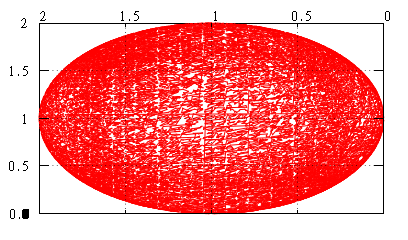
Полярная область ничем не выделяется, и это радует.

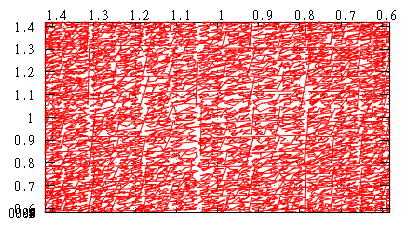
Она практически одинакова для обоих случаев.

Первые 1000 значений.

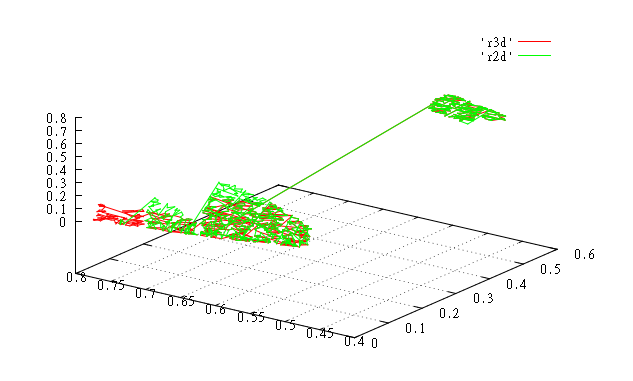Значения с 9000 по 10000.

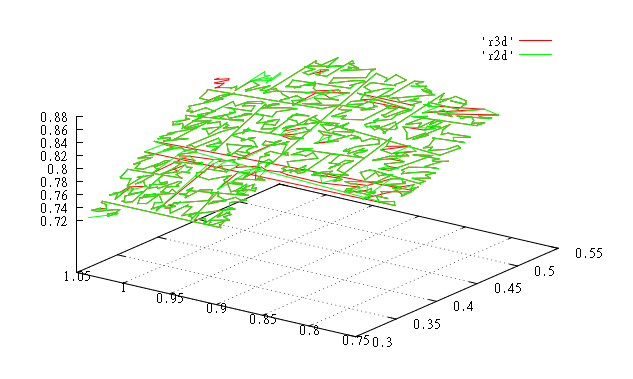Значения с 19000 по 20000.

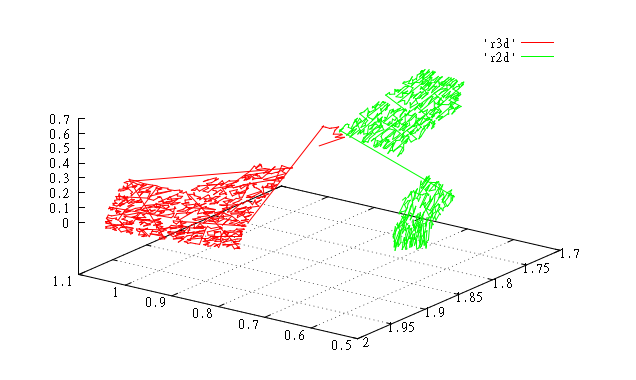Значения с 60000 по 61000.

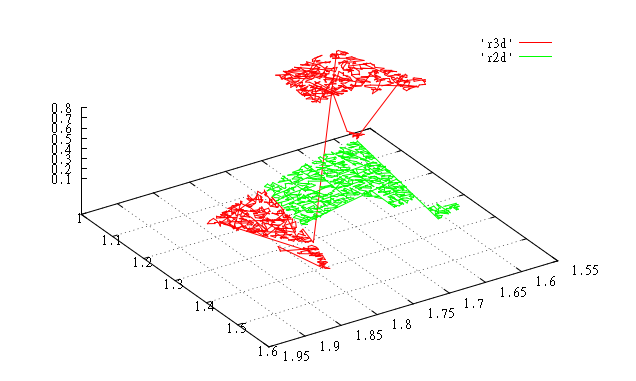Значения с 120000 по 121000.

Выводы

1. Как и ожидалось, псевдотрёхмерный (на сфере) пространственный индекс на основе заметающей кривой ведёт себя очень похоже на свой двухмерный вариант.
2. Он по-прежнему легко вычисляется.
3. Сам индекс реализуется в виде древовидной структуры, что очень удобно для СУБД.
4. Обладает всеми необходимыми качествами для индексации небесных объектов.

Впрочем, кроме достоинств, он обладает и всеми недостатками своего двухмерного варианта, причём в гипертрофированном виде. Если мы попытаемся искать в таком индексе «в лоб», выискивая непрерывные интервалы значений, нас ждёт разочарование, этих интервалов стало ещё больше. В сущности, «в лоб» можно искать только в очень небольших экстентах.

Как уже упоминалось, метод работы с таким индексом есть. Но это уже совсем другая история.

PS

Отдельное спасибо хочется выразить Саше Артюшину из компании DataEast за концептуальное участие.