Статья с разбором игры известной торговой сети вызвала у нас в Cloud4Y живой интерес. Вот небольшие отрывки, чтобы ввести вас в курс дела:

Автор статьи принялся расследовать причины своего проигрыша и по результатам расчетов выяснил следующее:
Прежде всего выясняем правила игры. В этом нам, сам того не зная, помог пользователь Хабра Stecenko в своем комментарии. Также он пишет:
В таких условиях расчет математической вероятности выигрыша несколько сложнее, чем предположил автор оригинального поста. Игра состоит из нескольких слоев:
Начнём с простого — с понимания как будет уменьшаться число участников при росте числа открытых ими карт из-за правила красной карточки.
Мы вычисляем, насколько вероятно, что за N испытаний (открытых карточек) будет открыта красная.
UPD: Первоначально мы рассчитывали вероятность открыть красную с помощью биномиального распределения. Это не гарантировало нам строго 1 красную карточку, при таком распределении вероятнее всего была одна красная карточка, но их могло быть как 0, так и все 9 с очень-очень маленькой вероятностью. Опять же, спасибо Stecenko за то, что в комментарии указал нам на ошибку и предложил верное решение.

В последнем столбце показано сколько игроков из ста остаются в игре с такой продолжительностью. Остальные игроки выбывают по причине красной карточки, так и не узнав, была ли выигрышная комбинация в выданном наборе карточек.
Теперь рассчитаем вероятности собрать комбинацию из трех карточек с одинаковыми товарами. Это является условием получения приза.
Разложим игру логически. Мы открываем первую карту, а затем под эту карту подбираем пару, под пару подбираем тройку. С таким подходом мы можем рассчитать вероятность получить 3 одинаковых карты за три или больше попыток, исходя из того, что всего товаров в игре 26.
Для задач с фиксированным числом тестов или испытаний, если результатом любого испытания может быть только успех или неудача, испытания независимы, а вероятность успеха остается постоянной в течение всего эксперимента будем использовать формулу Бернулли — в Excel функция БИНОМ.РАСП.
С помощью функции БИНОМ.РАСП можно вычислить, например, вероятность того, что двое из трех следующих новорожденных будут мальчиками. Какова вероятность открыть три одинаковые за три попытки?
=БИНОМ.РАСП(3;3;1/26;0) по маске
=БИНОМ.РАСП(число_успехов; число_испытаний; вероятность_успеха; интегральная)
Или вот формула для расчета вероятности получить 3 одинаковых и определенных товара за 8 попыток.
=БИНОМ.РАСП(3;8;1/26;0), так?
Не совсем. Когда мы достигли продолжительности игры в 4 испытания, не допустив открытия красной и продолжая играть, мы получаем ситуацию с возможностью двух пар для подбора выигрышной тройки.
Условно два товара из 26 — это А и Б. Наши открытые карточки А-Б-А-Б. Вероятность больше не 1/26, а 1/26+(1/26)*«Вероятность двух пар при данной продолжительности игры».
Вероятность двух пар при данной продолжительности игры = БИНОМ.РАСП(2;5;1/26;0)^2
При достижении большей длины игры к 7 попытке у нас появляется комбинации типа А-Б-А-Б-В-В. Это означает, что вероятность теперь равна
=1/26*(1 +БИНОМ.РАСП(2;7;1/26;0)^2 +БИНОМ.РАСП(2;7;1/26;0)^3) и мы ищем третью карту для 1, 2 или трёх пар.
UPD: Также первоначально мы не учли, что первая попытка в нашем расчете выигрыша, очищенного от вероятности выбрать красную, — это открытие любого из 26 товаров, а значит 100% успех. Количество повторов товара в матрице это количество совпадений с любым одним товаром, а значит для выигрыша достаточно двух повторов к одному товару, а не совпадения 3 с определенным загаданным результатом. Таким образом, первый выбор любой карты и две попытки подобрать ещё две такие же образуют в сумме три эксперимента.
Зная вероятности, мы строим матрицу:
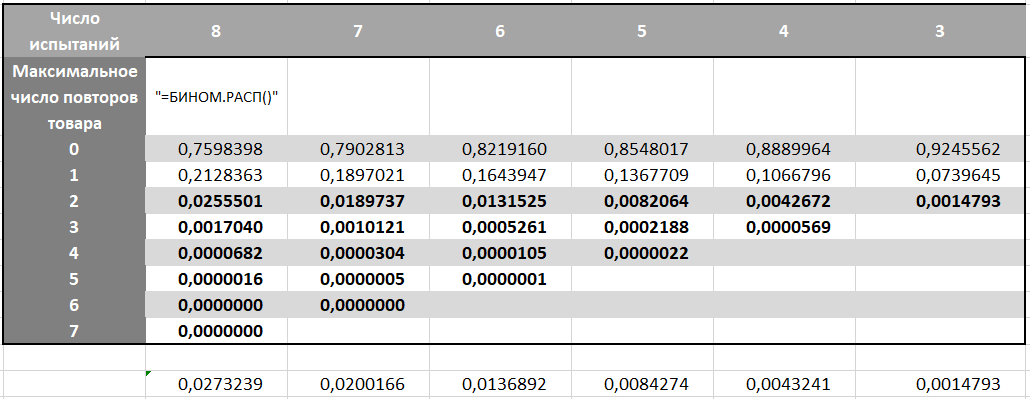
В ней мы находим вероятность каждого максимального количества повторов какого-либо товара для каждого варианта продолжительности игры. Помним, что вероятность выигрыша меняется на 4 попытке и на 7, а значит учитываем это в формуле БИНОМ.РАСП
Нам нужны варианты с максимальным количеством повторов какого-либо товара 3 и более. Так как игра прекратиться, как только мы соберем тройку, мы складываем вероятности по столбцам в области, выделенной жирным шрифтом.
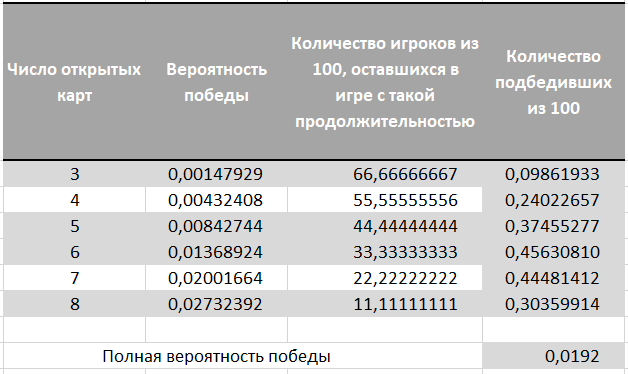
Далее мы перемножаем шансы каждой продолжительности игры на шансы выиграть приз при такой продолжительности. Суммируя эти произведения, мы получаем вероятность 0,0192 или 192 победителя на 10000 игроков.
Да, действительно это очень низкая вероятность. Совсем не 25%. Снова обратимся к правилам игры:
UPD: Итоговая вероятность изменилась после внесенных правок. Сейчас мы можем проверить наши вычисления на практике с помощью скриптов, но удивителен Божий дар ума математиков-теоретиков предыдущих поколений, которые рассчитывали такое количество вероятностей, находя верное решение на бумаге и с помощью мысленных экспериментов.
Анализ кода показал автору оригинальной публикации, что скрипт ещё до начала игры “знает” её итог, однако никто не знает какой предопределенный результат выдаст скрипт конкретному пользователю. Зная математическую сторону вопроса, вы сможете сами сделать вывод о честности организаторов.
Однажды, солнечным весенним утром, почитывая городской форум, я наткнулся на ссылку с простенькой игрой от известной торговой сети. Игра (акция), посвящённая чемпионату мира по футболу, представляла собой незамысловатое поле три на три, заполненное футбольными мячами. Кликая по мячу, мы открывали картинку с тем или иным товаром. При открытии трёх одинаковых картинок участнику гарантировалось бесплатное получение данного товара в одном из магазинов сети. Также под одним из мячей имелось изображение красной карточки, открытие которой означало конец игры.

Автор статьи принялся расследовать причины своего проигрыша и по результатам расчетов выяснил следующее:
Быстрый набросок формул на салфетке, и выяснилось, что вероятность выигрыша — 1/4. Для 5 полей пришлось повозиться, но расчётная вероятность получилась также 25%.Нас заинтересовала правильность такого расчета и, заменив салфетку на Excel, мы взялись за дело в поисках математической истины. Читателей, увлекающихся теорией вероятности, приглашаем под кат, дабы проверить правильность наших вычислений.
...
Запустив скрипт, я получил неожиданный результат — 25% выигрышей. Поиграв с количеством выигрышных элементов и общим количеством полей, я выяснил, что вероятность выигрыша в подобной игре не зависит от количества полей и равна единице, поделенной на количество выигрышных элементов, увеличенных на единицу.
Прежде всего выясняем правила игры. В этом нам, сам того не зная, помог пользователь Хабра Stecenko в своем комментарии. Также он пишет:
Если посмотреть скрипт автора, то он написан из предположения, что на поле ОБЯЗАТЕЛЬНО есть три карточки одного товара, по одной карточке еще пяти других товаров, и одна красная карточка, в то время как из описания игры этого абсолютно не следует — в правилах не сказано, что на поле обязана присутствовать выигрышная комбинация.В правилах, однако, сказано, что всего участвует 26 товаров. Получается, что генерируется выдача из 9 карт: 8 карт — это сочетания 26 товаров с повторениями, а одна карточка красная.
В таких условиях расчет математической вероятности выигрыша несколько сложнее, чем предположил автор оригинального поста. Игра состоит из нескольких слоев:
- Вероятность открыть N карт, не открывая красную — вероятность разной продолжительности игры без учета будет ли приз.
- Вероятность собрать комбинацию из 3 карт с одинаковыми товарами. Эта вероятность изменяется при разной продолжительности игры. Важно понимать, что набор из 8 карт с товарами и всегда одной красной не обязательно содержит хотя бы одну пару одинаковых карточек, не говоря о сразу трёх.
Начнём с простого — с понимания как будет уменьшаться число участников при росте числа открытых ими карт из-за правила красной карточки.
Шансы разной продолжительности игры
Мы вычисляем, насколько вероятно, что за N испытаний (открытых карточек) будет открыта красная.
UPD: Первоначально мы рассчитывали вероятность открыть красную с помощью биномиального распределения. Это не гарантировало нам строго 1 красную карточку, при таком распределении вероятнее всего была одна красная карточка, но их могло быть как 0, так и все 9 с очень-очень маленькой вероятностью. Опять же, спасибо Stecenko за то, что в комментарии указал нам на ошибку и предложил верное решение.

В последнем столбце показано сколько игроков из ста остаются в игре с такой продолжительностью. Остальные игроки выбывают по причине красной карточки, так и не узнав, была ли выигрышная комбинация в выданном наборе карточек.
Теперь рассчитаем вероятности собрать комбинацию из трех карточек с одинаковыми товарами. Это является условием получения приза.
Шансы на призы
Разложим игру логически. Мы открываем первую карту, а затем под эту карту подбираем пару, под пару подбираем тройку. С таким подходом мы можем рассчитать вероятность получить 3 одинаковых карты за три или больше попыток, исходя из того, что всего товаров в игре 26.
Для задач с фиксированным числом тестов или испытаний, если результатом любого испытания может быть только успех или неудача, испытания независимы, а вероятность успеха остается постоянной в течение всего эксперимента будем использовать формулу Бернулли — в Excel функция БИНОМ.РАСП.
С помощью функции БИНОМ.РАСП можно вычислить, например, вероятность того, что двое из трех следующих новорожденных будут мальчиками. Какова вероятность открыть три одинаковые за три попытки?
=БИНОМ.РАСП(3;3;1/26;0) по маске
=БИНОМ.РАСП(число_успехов; число_испытаний; вероятность_успеха; интегральная)
Или вот формула для расчета вероятности получить 3 одинаковых и определенных товара за 8 попыток.
=БИНОМ.РАСП(3;8;1/26;0), так?
Не совсем. Когда мы достигли продолжительности игры в 4 испытания, не допустив открытия красной и продолжая играть, мы получаем ситуацию с возможностью двух пар для подбора выигрышной тройки.
Условно два товара из 26 — это А и Б. Наши открытые карточки А-Б-А-Б. Вероятность больше не 1/26, а 1/26+(1/26)*«Вероятность двух пар при данной продолжительности игры».
Вероятность двух пар при данной продолжительности игры = БИНОМ.РАСП(2;5;1/26;0)^2
При достижении большей длины игры к 7 попытке у нас появляется комбинации типа А-Б-А-Б-В-В. Это означает, что вероятность теперь равна
=1/26*(1 +БИНОМ.РАСП(2;7;1/26;0)^2 +БИНОМ.РАСП(2;7;1/26;0)^3) и мы ищем третью карту для 1, 2 или трёх пар.
UPD: Также первоначально мы не учли, что первая попытка в нашем расчете выигрыша, очищенного от вероятности выбрать красную, — это открытие любого из 26 товаров, а значит 100% успех. Количество повторов товара в матрице это количество совпадений с любым одним товаром, а значит для выигрыша достаточно двух повторов к одному товару, а не совпадения 3 с определенным загаданным результатом. Таким образом, первый выбор любой карты и две попытки подобрать ещё две такие же образуют в сумме три эксперимента.
Зная вероятности, мы строим матрицу:

В ней мы находим вероятность каждого максимального количества повторов какого-либо товара для каждого варианта продолжительности игры. Помним, что вероятность выигрыша меняется на 4 попытке и на 7, а значит учитываем это в формуле БИНОМ.РАСП
Нам нужны варианты с максимальным количеством повторов какого-либо товара 3 и более. Так как игра прекратиться, как только мы соберем тройку, мы складываем вероятности по столбцам в области, выделенной жирным шрифтом.

Далее мы перемножаем шансы каждой продолжительности игры на шансы выиграть приз при такой продолжительности. Суммируя эти произведения, мы получаем вероятность 0,0192 или 192 победителя на 10000 игроков.
Да, действительно это очень низкая вероятность. Совсем не 25%. Снова обратимся к правилам игры:
8. Призовой фонд:116000 делим на вероятность выигрыша и получаем около 6 млн участников для того, чтобы разыграть все призы. Напомним, что на 1 января 2018 года по оценке Росстата в России было 146 938 921 постоянных жителей. Видимо, такова задумка организаторов игры — предоставить шанс выиграть почти каждому гражданину России.
8.1. Доступные призы: названия и количества
…
Итого 166000
UPD: Итоговая вероятность изменилась после внесенных правок. Сейчас мы можем проверить наши вычисления на практике с помощью скриптов, но удивителен Божий дар ума математиков-теоретиков предыдущих поколений, которые рассчитывали такое количество вероятностей, находя верное решение на бумаге и с помощью мысленных экспериментов.
Анализ кода показал автору оригинальной публикации, что скрипт ещё до начала игры “знает” её итог, однако никто не знает какой предопределенный результат выдаст скрипт конкретному пользователю. Зная математическую сторону вопроса, вы сможете сами сделать вывод о честности организаторов.