В сложных ERP-системах многие сущности имеют иерархическую природу, когда однородные объекты выстраиваются в дерево отношений «предок — потомок» — это и организационная структура предприятия (все эти филиалы, отделы и рабочие группы), и каталог товаров, и участки работ, и география точек продаж,…

Фактически, нет ни одной сферы автоматизации бизнеса, где хоть какой-нибудь иерархии да не оказалось бы в результате. Но даже если вы не работаете «на бизнес», все равно можете легко столкнуться с иерархичными связями. Банально, даже ваше генеалогическое древо или поэтажная схема помещений в торговом центре — такая же структура.
Существует много способов хранения такого дерева в СУБД, но мы сегодня остановимся только на одном варианте:
И пока вы всматриваетесь в глубину иерархии, она терпеливо ждет, насколько же [не]эффективными окажутся ваши «наивные» способы работы с такой структурой.

Давайте разберем типовые возникающие задачи, их реализацию на SQL и попробуем улучшить их производительность.
Давайте, для определенности, примем, что эта структура у нас будет отражать подчиненность отделов в структуре организации: департаменты, дивизионы, секторы, филиалы, рабочие группы,… — как их ни назови.
Начнем с самой простой задачи — найти всех сотрудников, которые работают внутри конкретного сектора, или в терминах иерархии — найти всех потомков узла. А еще и «глубину» потомка неплохо бы получить… Все это может быть необходимо, например, для построения какой-то сложной выборки по списку ID этих сотрудников.
Все бы ничего, если этих потомков там всего пара уровней и количественно в пределах десятка, но если уровней больше 5, а потомков уже десятки — могут быть проблемы. Давайте посмотрим, как пишутся (и работают) традиционные варианты поиска «вниз по дереву». Но сначала определим, какие из узлов будут наиболее интересными для наших исследований.
Самые «глубокие» поддеревья:
Самые «широкие» поддеревья:
Для этих запросов мы воспользовались типичным рекурсивным JOIN:
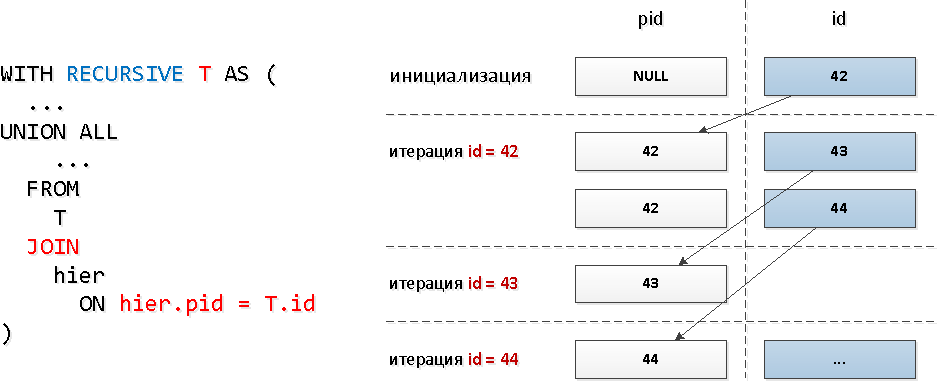
Очевидно, при такой модели запроса количество итераций будет совпадать с общим количеством потомков (а их ведь несколько десятков), и занимать это может достаточно существенные ресурсы, и, как следствие, время.
Проверим на самом «широком» поддереве:
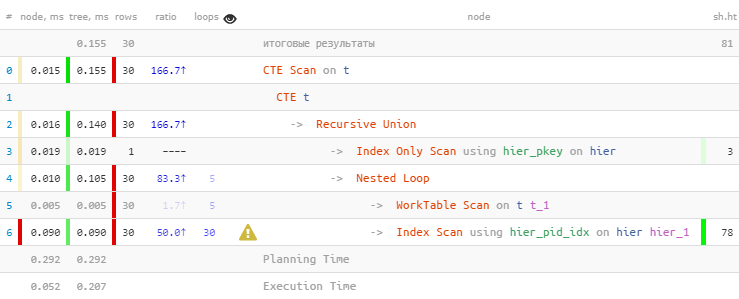
[посмотреть на explain.tensor.ru]
Как и предполагали, мы нашли все 30 записей. Но потратили на это 60% всего времени — потому что сделали при этом и 30 поисков по индексу. А меньше — можно?
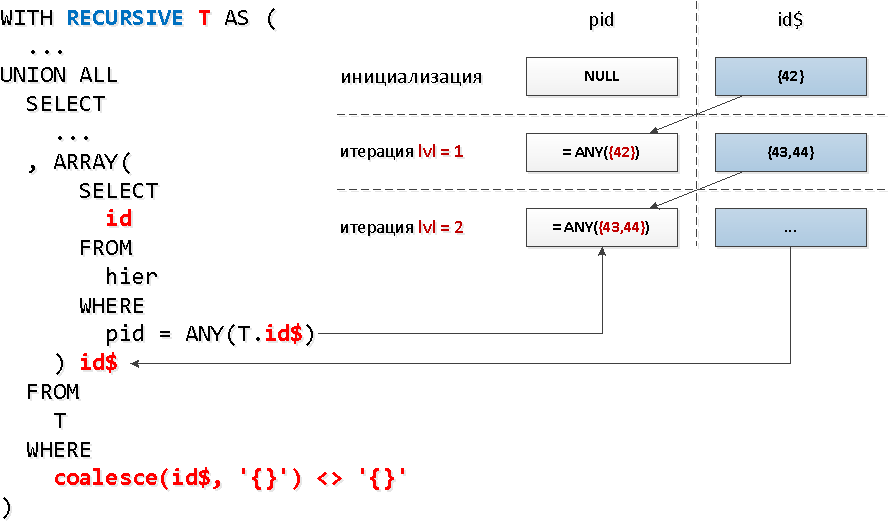
А для каждого ли узла нам необходимо делать отдельный запрос к индексу? Оказывается, нет — читать из индекса мы можем сразу по нескольким ключам за одно обращение с помощью
А в каждую такую группу идентификаторов мы можем взять все найденные на предыдущем шаге ID по «узлам». То есть на каждом следующем шаге мы будем искать сразу вообще всех потомков определенного уровня.
Только, вот незадача, в рекурсивной выборке нельзя обратиться к самой себе во вложенном запросе, а нам ведь надо как-то отобрать именно только найденное на предыдущем уровне… Оказывается, сделать вложенный запрос ко всей выборке — нельзя, а вот к ее конкретному полю — можно. А это поле может быть и массивом — что нам и нужно для использования
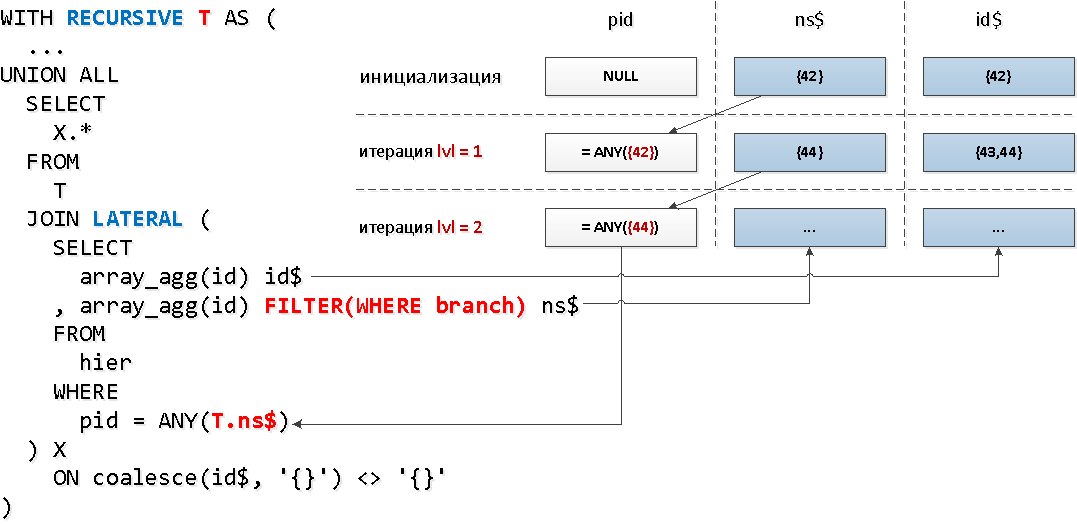
Звучит несколько дико, но на схеме — все просто.
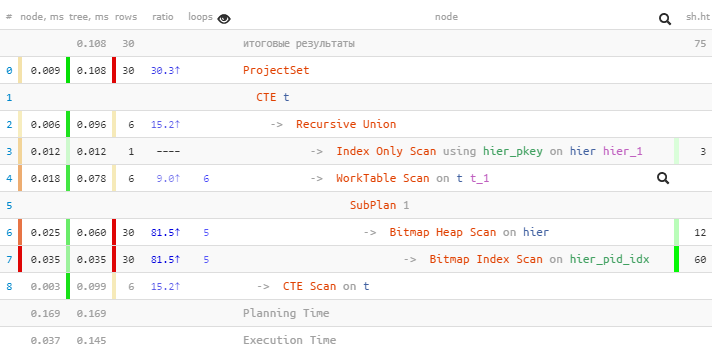
[посмотреть на explain.tensor.ru]
И тут самым важным является даже не выигрыш в 1.5 раза по времени, а что мы вычитали меньше buffers, поскольку обращений к индексу у нас всего 5 вместо 30!
Дополнительным бонусом идет тот факт, что после финального unnest идентификаторы останутся упорядочеными по «уровням».
Следующее соображение, которое поможет улучшить производительность — у «листьев» не может быть детей, то есть для них искать «вниз» вообще ничего не надо. В постановке нашей задачи это означает, что если мы шли по цепочке отделов и дошли до сотрудника, то дальше по этой ветке искать уже незачем.
Давайте введем в нашу таблицу дополнительное
Отлично! Оказывается у нас только чуть больше 30% всех элементов дерева имеют потомков.
Теперь применим несколько иную механику — соединения с рекурсивной частью через
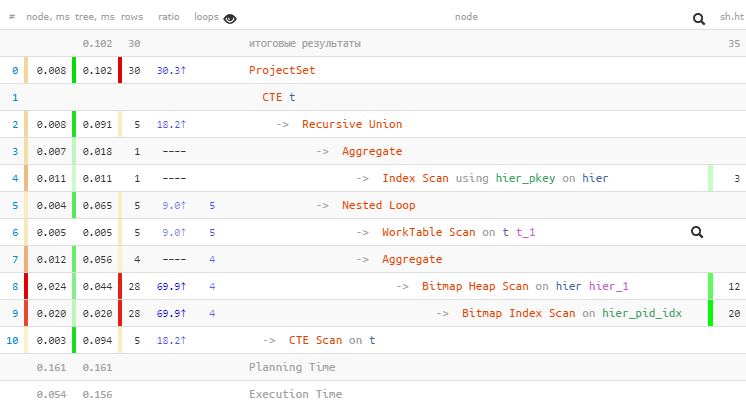
[посмотреть на explain.tensor.ru]
Мы смогли сократить еще одно обращение к индексу и выиграли более чем в 2 раза по объему вычитываемого.
Этот алгоритм будет полезен, если вам необходимо собрать записи для всех элементов «вверх по дереву», сохранив при этом информацию, каким исходным листом (и с какими показателями) вызвано его попадание в выборку — например, для формирования сводного отчета с агрегацией на узлы.
Дальнейшее стоит воспринимать исключительно как proof-of-concept, поскольку запрос получается очень уж громоздкий. Но если он доминирует в вашей базе — стоит задуматься над применением подобных методик.
Начнем с пары простых утверждений:
Теперь попробуем сконструировать нужный нам запрос.
Очевидно, что на инициализации рекурсии (куда же без нее!) нам придется вычитать записи самих листьев по набору исходных идентификаторов:
Если кому-то показалось странным, что «набор» хранится строкой, а не массивом, то этому есть простое объяснение. Для строк существует встроенная агрегирующая «склеивающая» функция
Теперь нам бы получить набор ID разделов, которые надо будет вычитать дальше. Почти всегда они будут дублироваться у разных записей исходного набора — поэтому нам бы их сгруппировать, сохранив при этом информацию о листьях-источниках.
Но тут нас поджидают три неприятности:
К счастью, все эти проблемы достаточно легко обходятся. Начнем с конца.
Вот так не работает:
А так — работает, скобочки решают!
Хм… Обращение к рекурсивной CTE не может быть во вложенном запросе. Но оно может быть внутри CTE! А вложенный запрос может обращаться уже к этой CTE!
Неприятно, но… У нас же есть простой способ, как можно сэмулировать GROUP BY с помощью
А вот так — работает!
Вот теперь мы видим, зачем числовой ID превращался в текст — чтобы их можно было склеивать через запятую!
Для финала нам осталось всего ничего:
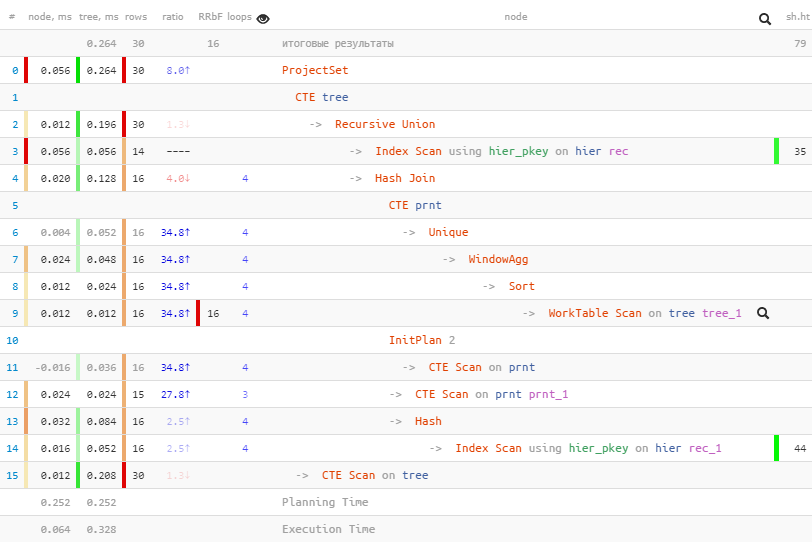
[посмотреть на explain.tensor.ru]

Фактически, нет ни одной сферы автоматизации бизнеса, где хоть какой-нибудь иерархии да не оказалось бы в результате. Но даже если вы не работаете «на бизнес», все равно можете легко столкнуться с иерархичными связями. Банально, даже ваше генеалогическое древо или поэтажная схема помещений в торговом центре — такая же структура.
Существует много способов хранения такого дерева в СУБД, но мы сегодня остановимся только на одном варианте:
CREATE TABLE hier(
id
integer
PRIMARY KEY
, pid
integer
REFERENCES hier
, data
json
);
CREATE INDEX ON hier(pid); -- не забываем, что FK не подразумевает автосоздание индекса, в отличие от PK
И пока вы всматриваетесь в глубину иерархии, она терпеливо ждет, насколько же [не]эффективными окажутся ваши «наивные» способы работы с такой структурой.

Давайте разберем типовые возникающие задачи, их реализацию на SQL и попробуем улучшить их производительность.
#1. Насколько глубока кроличья нора?
Давайте, для определенности, примем, что эта структура у нас будет отражать подчиненность отделов в структуре организации: департаменты, дивизионы, секторы, филиалы, рабочие группы,… — как их ни назови.

Сначала нагенерируем наше 'дерево' из 10K элементов
INSERT INTO hier
WITH RECURSIVE T AS (
SELECT
1::integer id
, '{1}'::integer[] pids
UNION ALL
SELECT
id + 1
, pids[1:(random() * array_length(pids, 1))::integer] || (id + 1)
FROM
T
WHERE
id < 10000
)
SELECT
pids[array_length(pids, 1)] id
, pids[array_length(pids, 1) - 1] pid
FROM
T;Начнем с самой простой задачи — найти всех сотрудников, которые работают внутри конкретного сектора, или в терминах иерархии — найти всех потомков узла. А еще и «глубину» потомка неплохо бы получить… Все это может быть необходимо, например, для построения какой-то сложной выборки по списку ID этих сотрудников.
Все бы ничего, если этих потомков там всего пара уровней и количественно в пределах десятка, но если уровней больше 5, а потомков уже десятки — могут быть проблемы. Давайте посмотрим, как пишутся (и работают) традиционные варианты поиска «вниз по дереву». Но сначала определим, какие из узлов будут наиболее интересными для наших исследований.
Самые «глубокие» поддеревья:
WITH RECURSIVE T AS (
SELECT
id
, pid
, ARRAY[id] path
FROM
hier
WHERE
pid IS NULL
UNION ALL
SELECT
hier.id
, hier.pid
, T.path || hier.id
FROM
T
JOIN
hier
ON hier.pid = T.id
)
TABLE T ORDER BY array_length(path, 1) DESC; id | pid | path
---------------------------------------------
7624 | 7623 | {7615,7620,7621,7622,7623,7624}
4995 | 4994 | {4983,4985,4988,4993,4994,4995}
4991 | 4990 | {4983,4985,4988,4989,4990,4991}
...Самые «широкие» поддеревья:
...
SELECT
path[1] id
, count(*)
FROM
T
GROUP BY
1
ORDER BY
2 DESC;id | count
------------
5300 | 30
450 | 28
1239 | 27
1573 | 25
Для этих запросов мы воспользовались типичным рекурсивным JOIN:

Очевидно, при такой модели запроса количество итераций будет совпадать с общим количеством потомков (а их ведь несколько десятков), и занимать это может достаточно существенные ресурсы, и, как следствие, время.
Проверим на самом «широком» поддереве:
WITH RECURSIVE T AS (
SELECT
id
FROM
hier
WHERE
id = 5300
UNION ALL
SELECT
hier.id
FROM
T
JOIN
hier
ON hier.pid = T.id
)
TABLE T;
[посмотреть на explain.tensor.ru]
Как и предполагали, мы нашли все 30 записей. Но потратили на это 60% всего времени — потому что сделали при этом и 30 поисков по индексу. А меньше — можно?
Массовая вычитка по индексу
А для каждого ли узла нам необходимо делать отдельный запрос к индексу? Оказывается, нет — читать из индекса мы можем сразу по нескольким ключам за одно обращение с помощью
= ANY(array).А в каждую такую группу идентификаторов мы можем взять все найденные на предыдущем шаге ID по «узлам». То есть на каждом следующем шаге мы будем искать сразу вообще всех потомков определенного уровня.
Только, вот незадача, в рекурсивной выборке нельзя обратиться к самой себе во вложенном запросе, а нам ведь надо как-то отобрать именно только найденное на предыдущем уровне… Оказывается, сделать вложенный запрос ко всей выборке — нельзя, а вот к ее конкретному полю — можно. А это поле может быть и массивом — что нам и нужно для использования
ANY.Звучит несколько дико, но на схеме — все просто.

WITH RECURSIVE T AS (
SELECT
ARRAY[id] id$
FROM
hier
WHERE
id = 5300
UNION ALL
SELECT
ARRAY(
SELECT
id
FROM
hier
WHERE
pid = ANY(T.id$)
) id$
FROM
T
WHERE
coalesce(id$, '{}') <> '{}' -- условие выхода из цикла - пустой массив
)
SELECT
unnest(id$) id
FROM
T;
[посмотреть на explain.tensor.ru]
И тут самым важным является даже не выигрыш в 1.5 раза по времени, а что мы вычитали меньше buffers, поскольку обращений к индексу у нас всего 5 вместо 30!
Дополнительным бонусом идет тот факт, что после финального unnest идентификаторы останутся упорядочеными по «уровням».
Признак узла
Следующее соображение, которое поможет улучшить производительность — у «листьев» не может быть детей, то есть для них искать «вниз» вообще ничего не надо. В постановке нашей задачи это означает, что если мы шли по цепочке отделов и дошли до сотрудника, то дальше по этой ветке искать уже незачем.
Давайте введем в нашу таблицу дополнительное
boolean-поле, которое будет нам сразу говорить, является ли эта вот конкретная запись в нашем дереве «узлом» — то есть могут ли у него вообще существовать потомки.ALTER TABLE hier
ADD COLUMN branch boolean;
UPDATE
hier T
SET
branch = TRUE
WHERE
EXISTS(
SELECT
NULL
FROM
hier
WHERE
pid = T.id
LIMIT 1
);
-- Запрос успешно выполнен: 3033 строк изменено за 42 мс.Отлично! Оказывается у нас только чуть больше 30% всех элементов дерева имеют потомков.
Теперь применим несколько иную механику — соединения с рекурсивной частью через
LATERAL, что позволит нам сразу обратиться к полям рекурсивной «таблицы», а агрегатную функцию с условием фильтрации по признаку узла используем для уменьшения набора ключей:
WITH RECURSIVE T AS (
SELECT
array_agg(id) id$
, array_agg(id) FILTER(WHERE branch) ns$
FROM
hier
WHERE
id = 5300
UNION ALL
SELECT
X.*
FROM
T
JOIN LATERAL (
SELECT
array_agg(id) id$
, array_agg(id) FILTER(WHERE branch) ns$
FROM
hier
WHERE
pid = ANY(T.ns$)
) X
ON coalesce(T.ns$, '{}') <> '{}'
)
SELECT
unnest(id$) id
FROM
T;
[посмотреть на explain.tensor.ru]
Мы смогли сократить еще одно обращение к индексу и выиграли более чем в 2 раза по объему вычитываемого.
#2. Вернемся к корням
Этот алгоритм будет полезен, если вам необходимо собрать записи для всех элементов «вверх по дереву», сохранив при этом информацию, каким исходным листом (и с какими показателями) вызвано его попадание в выборку — например, для формирования сводного отчета с агрегацией на узлы.

Дальнейшее стоит воспринимать исключительно как proof-of-concept, поскольку запрос получается очень уж громоздкий. Но если он доминирует в вашей базе — стоит задуматься над применением подобных методик.
Начнем с пары простых утверждений:
- Одну и ту же запись из базы лучше читать всего один раз.
- Записи из базы эффективнее читать «пачкой», чем поодиночке.
Теперь попробуем сконструировать нужный нам запрос.
Шаг 1
Очевидно, что на инициализации рекурсии (куда же без нее!) нам придется вычитать записи самих листьев по набору исходных идентификаторов:
WITH RECURSIVE tree AS (
SELECT
rec -- это цельная запись таблицы
, id::text chld -- это "набор" приведших сюда исходных листьев
FROM
hier rec
WHERE
id = ANY('{1,2,4,8,16,32,64,128,256,512,1024,2048,4096,8192}'::integer[])
UNION ALL
...Если кому-то показалось странным, что «набор» хранится строкой, а не массивом, то этому есть простое объяснение. Для строк существует встроенная агрегирующая «склеивающая» функция
string_agg, а для массивов — нет. Хотя ее и несложно реализовать самостоятельно.Шаг 2
Теперь нам бы получить набор ID разделов, которые надо будет вычитать дальше. Почти всегда они будут дублироваться у разных записей исходного набора — поэтому нам бы их сгруппировать, сохранив при этом информацию о листьях-источниках.
Но тут нас поджидают три неприятности:
- «Подрекурсивная» часть запроса не может содержать агрегатных функций с
GROUP BY. - Обращение к рекурсивной «таблице» не может находиться во вложенном подзапросе.
- Запрос в рекурсивной части не может содержать CTE.
К счастью, все эти проблемы достаточно легко обходятся. Начнем с конца.
CTE в рекурсивной части
Вот так не работает:
WITH RECURSIVE tree AS (
...
UNION ALL
WITH T (...)
SELECT ...
)А так — работает, скобочки решают!
WITH RECURSIVE tree AS (
...
UNION ALL
(
WITH T (...)
SELECT ...
)
)Вложенный запрос к рекурсивной «таблице»
Хм… Обращение к рекурсивной CTE не может быть во вложенном запросе. Но оно может быть внутри CTE! А вложенный запрос может обращаться уже к этой CTE!
GROUP BY внутри рекурсии
Неприятно, но… У нас же есть простой способ, как можно сэмулировать GROUP BY с помощью
DISTINCT ON и оконных функций!SELECT
(rec).pid id
, string_agg(chld::text, ',') chld
FROM
tree
WHERE
(rec).pid IS NOT NULL
GROUP BY 1 -- не работает!А вот так — работает!
SELECT DISTINCT ON((rec).pid)
(rec).pid id
, string_agg(chld::text, ',') OVER(PARTITION BY (rec).pid) chld
FROM
tree
WHERE
(rec).pid IS NOT NULLВот теперь мы видим, зачем числовой ID превращался в текст — чтобы их можно было склеивать через запятую!
Шаг 3
Для финала нам осталось всего ничего:
- вычитываем записи «разделов» по набору сгруппированных ID
- сопоставляем вычитанные разделы с «наборами» исходных листов
- «разворачиваем» строку-набор с помощью
unnest(string_to_array(chld, ',')::integer[])
WITH RECURSIVE tree AS (
SELECT
rec
, id::text chld
FROM
hier rec
WHERE
id = ANY('{1,2,4,8,16,32,64,128,256,512,1024,2048,4096,8192}'::integer[])
UNION ALL
(
WITH prnt AS (
SELECT DISTINCT ON((rec).pid)
(rec).pid id
, string_agg(chld::text, ',') OVER(PARTITION BY (rec).pid) chld
FROM
tree
WHERE
(rec).pid IS NOT NULL
)
, nodes AS (
SELECT
rec
FROM
hier rec
WHERE
id = ANY(ARRAY(
SELECT
id
FROM
prnt
))
)
SELECT
nodes.rec
, prnt.chld
FROM
prnt
JOIN
nodes
ON (nodes.rec).id = prnt.id
)
)
SELECT
unnest(string_to_array(chld, ',')::integer[]) leaf
, (rec).*
FROM
tree;
[посмотреть на explain.tensor.ru]