
Любой, кто, так или иначе, сталкивался с криптографией, знает, что без генераторов случайных чисел в этом деле не обойтись. Одно из возможных применений таких генераторов, например, – генерация ключей. Но не каждый при этом задумывается, а насколько «хорош» тот или иной генератор. А если и задумывался, то сталкивался с тем фактом, что в мире не существует какого-либо единственного «официального» набора критериев, который бы оценивал, насколько данные случайные числа применимы именно для данной области криптографии. Если последовательность случайных чисел предсказуема, то даже самый стойкий алгоритм шифрования, в котором данная последовательность будет использоваться, оказывается, уязвим — например, резко уменьшается пространство возможных ключей, которые необходимо «перебрать» злоумышленнику для получения некоторой информации, с помощью которой он сможет «взломать» всю систему. К счастью, разные организации все же пытаются навести здесь порядок, в частности, американский институт по стандартам NIST разработал набор тестов для оценки случайности последовательности чисел. О них и пойдет речь в данной статье. Но сначала — немного теории (постараюсь изложить не нудно).
Случайные двоичные последовательности
Во-первых, под генерацией случайных чисел подразумевается получение последовательности из двоичных знаков 0 и 1, а не байтами, как бы ни хотелось программистам. Идеальным подобным генератором является подбрасывание «идеальной» монеты (ровная монета, у которой вероятности выпадения каждой из сторон одинаковы), которую бы подбрасывали столько раз, сколько нужно, но проблема в том, ничего идеального не сущ ествует, а производительность такого генератора оставляла бы желать лучшего (один подрос монеты = одному биту). Тем не менее, все тесты, описываемые ниже, оценивают, насколько исследуемый генератор случайных чисел «похож» или «не похож» на воображаемую идеальную монету (не по скорости получения «случайных» знаков, а их «качества»).
Во-вторых, все генераторы случайных чисел делятся на 2 типа —истинно случайные — физические генераторы/датчики случайных чисел (ДСЧ/ФДСЧ) и псевдослучайные – программные датчики/генераторы случайных чисел (ПДСЧ). Первые принимают на вход некий случайный бесконечный процесс, а на выходе дают бесконечную (зависит от времени наблюдения) последовательность 0 и 1. Вторые представляют собой заданную разработчиком детерминированную функцию, которая инициализируется т. н. зерном, после чего также на выходе выдает последовательность 0 и 1. Зная это зерно, можно предсказать всю последовательность. Хороший ПДСЧ — этот тот, для которого невозможно предсказать последующие значения, имея всю историю предыдущих значений, не имея зерна. Это свойство называется прямой непредсказуемостью. Есть еще обратная непредсказуемость — невозможность вычислить зерно, зная любое количество генерируемых значений.
Казалось бы, проще всего взять истинно случайные/физические ДСЧ и не думать ни о какой предсказуемости. Однако тут есть проблемы:
- Случайное явление/процесс, которое берется за основу, может быть не способно выдавать числа с нужной скоростью. Если вы вспоминаете, когда последний раз генерировали пару 2048битных ключей, то не обольщайтесь. Это происходит очень редко? Тогда вообразите себя сервером, принимающим сотни запросов на SSL-соединения в секунду (SSL handshake предполагает генерацию пары случайных чисел).
- С виду случайные явления могут быть не такими случайными, как казалось бы. Например, электромагнитный шум может быть суперпозицией нескольких более-менее однообразных периодических сигналов.
Каждый из тестов, предлагаемых NIST, получает на вход конечную последовательность. Далее вычисляется статистика, характеризующая некое свойство данной последовательности — это может быть и единичное значение, и множество значений. После чего эта статистика сравнивается с эталонной статистикой, которую даст идеально случайная последовательность. Эталонная статистика выводится математически, этому посвящено множество теорем и научных трудов. В конце статьи будут даны все ссылки на источники, где выводятся нужные формулы.
Нулевая и альтернативная гипотезы
В основе тестов лежит понятие нулевой гипотезы. Попробую объяснить, что это. Допустим, мы набрали некую статистическую информацию. Например, пусть это будет количество людей, заболевших раком легких в группе из 1000 человек. И пусть известно, что некоторые люди из этой группы являются курильщиками, а другие нет, причем известно, какие конкретно. Стоит следующая задача: понять, есть ли взаимосвязь между курением и заболеванием. Нулевая гипотеза — это предположение, что между двумя фактами отсутствует какая-либо взаимосвязь. В нашем примере это предположение, что курение не вызывает рак легких. Существует также альтернативная гипотеза, которая опровергает нулевую гипотезу: т.е. между явлениями взаимосвязь существует (курение вызывает рак легких). Если переходить к терминам случайных чисел, то за нулевую гипотезу принимается предположение, что последовательность является истинно случайной (знаки которой появляются равновероятно и независимо друг от друга). Следовательно, если нулевая гипотеза верна, то наш генератор производит достаточно «хорошие» случайные числа.
Как проверяется гипотеза? С одной стороны, мы имеем статистику, подсчитанную на основе фактически собранных данных (т.е. по измеряемой последовательности). С другой стороны, есть эталонная статистика, получаемая математическими методами (теоретически вычисленная), которую бы имела истинно случайная последовательность. Очевидно, что собранная статистика не может сравняться с эталонной — насколько бы ни был хорошо наш генератор, он все равно не идеален. Поэтому вводят некую погрешность, например 5%. Она означает, что если, например, собранная статистика отклоняется от эталонной больше чем на 5%, то делается вывод о том, что нулевая гипотеза не верна с большой надежностью.
Так как мы имеем дело с гипотезами, то существует 4 варианта развития событий:
- Сделан вывод о том, что последовательность случайна, и это верный вывод
- Сделан вывод о том, что последовательность не случайна, хотя она была на самом деле случайна. Такие ошибки называют ошибками первого рода
- Последовательность признана случайной, хотя на самом деле таковой не является. Такие ошибки называют ошибками второго рода
- Последовательность справедливо отбракована
Вероятность ошибки первого рода называют уровнем статистической значимости и обозначают как α. Т.е. α — это вероятность отбраковать «хорошую» случайную последовательность. Это значение определяется областью применения. В криптографии принято α брать от 0.001 до 0.01.
В каждом тесте вычисляется т.н. P-значение: это вероятность того, что подопытный генератор произведет последовательность не хуже, чем гипотетический истинный. Если Pзначение = 1, то наша последовательность идеально случайна, а если оно = 0, то последовательность полностью предсказуема. В дальнейшем P-значение сравнивается с α, и если она больше α, то нулевая гипотеза принимается и последовательность признается случайной. В противном случае — отбраковывается.
В тестах берется α = 0.01. Из этого следует, что:
- Если P-значение ≥ 0.01, то последовательность признается случайной с уровнем доверия 99%
- Если P-значение < 0.01, то последовательность отбраковывается с уровнем доверия 99%
Итак, перейдем непосредственно к тестам.
Частотный побитовый тест
Очевидно, что чем более случайна последовательность, тем ближе это соотношение к 1. Данный тест оценивает, насколько это соотношение близко к 1.
Принимаем каждую «1» за +1, а каждый «0» за -1 и считаем сумму по всей последовательности. Это можно записать так:
Sn = X1 + X2 +… + Xn, где Xi = 2xi — 1.
Кстати, говорят, что распределение количества «успехов» в серии экспериментов, где в каждом эксперименте возможен успех или неуспех с заданной вероятностью, имеет биномиальное распределение.
Возьмем такую последовательность: 1011010101
Тогда S = 1 + (-1) + 1 + 1 + (-1) + 1 + (-1) + 1 + (-1) + 1 = 2
Вычисляем статистику:
Вычисляем P-значение через дополнительную функцию ошибок:
Дополнительная функция ошибок (complementary error function) определяется так:
Видим, что результат > 0.01, а значит наша последовательность прошла тест. Рекомендуется тестировать последовательности длиной не менее 100 бит.
Частотный блочный тест
Этот тест делается на основе предыдущего, только теперь значения пропорции «1»/«0» для каждого блока анализируются методом Хи-квадрат. Ясно, что это соотношение должно быть приблизительно равным 1.
Например, пусть дана последовательность 0110011010. Разобъем ее на блоки по 3 бита («бесхозный» 0 на конце отброшен):
011 001 101
Посчитаем пропорции πi для каждого блока: π1 = 2/3, π2 = 1/3, π3 = 1/3. Далее вычисляем статистику по методу Хи-квадрат c N степенями свободы (здесь N — количество блоков):
Вычислим P-значение через специальную функцию Q:
Q — это т.н. неполная верхняя гамма-функция, определяемая как:
При этом функция Г — стандартная гамма-функция:
Последовательность считается случайной, если P-значение > 0.01. Рекомендуется анализировать последовательности длиной не менее 100 бит, а также должны выполняться соотношения M >= 20, M > 0.01n и N < 100.
Тест на одинаковые идущие подряд биты
В тесте ищутся все последовательности одинаковых битов, а затем анализируется, насколько количество и размеры этих последовательностей соответствуют количеству и размерам истинно случайной последовательности. Смысл в том, что если смена 0 на 1 (и обратно) происходит слишом редко, то такая последовательность «не тянет» на случайную.
Пусть дана последовательность 1001101011. Сначала вычисляем долю единиц в общей массе:
Дальше проверяется условие:
Если оно не удовлетворяется, то весь тест считается неуспешным и на этом все заканчивается. В нашем случае 0.63246 > 0.1, а значит идем дальше.
Вычисляем суммарное число знакоперемен V:
где
Вычисляем P-значение через функцию ошибок:

Если результат >= 0.01 (как в нашем примере), то последовательность признается случайной.
Тест на самую длинную последовательность из единиц в блоке
Исходная последовательность из n битов разбивается на N блоков, каждый по M бит, после чего в каждом блоке ищется самая длинная последовательность единиц, а затем оценивается, насколько показатель близок к такому же показателю для истинно случайной последовательности. Очевидно, что аналогичного теста на нули не требуется, так как если единицы распределены хорошо, то нули также будут распределены хорошо.
Какую взять длину блока? NIST рекомендует несколько опорных значений, как разбивать на блоки:
| Общая длина, n | Длина блока, M |
|---|---|
| 128 | 8 |
| 6272 | 128 |
| 750000 | 10000 |
Пусть дана последовательность:
11001100 00010101 01101100 01001100 11100000 00000010
01001101 01010001 00010011 11010110 10000000 11010111
11001100 11100110 11011000 10110010
Разобьем ее на блоки по 8 бит (M=8), после чего посчитаем максимальную последовательность из единиц для каждого блока:
| Блок | Длина единиц |
|---|---|
| 11001100 | 2 |
| 00010101 | 1 |
| 01101100 | 2 |
| 01001100 | 2 |
| 11100000 | 3 |
| 00000010 | 1 |
| 01001101 | 2 |
| 01010001 | 1 |
| 00010011 | 2 |
| 11010110 | 2 |
| 10000000 | 1 |
| 11010111 | 3 |
| 11001100 | 2 |
| 11100110 | 3 |
| 11011000 | 2 |
| 10110010 | 2 |
Далее считаем статистику по разным длинам на основе следующей таблицы:
| vi | M = 8 | M = 128 | M = 10000 |
|---|---|---|---|
| v0 | ≤1 | &le4 | &le10 |
| v1 | 2 | 5 | 11 |
| v2 | 3 | 6 | 12 |
| v3 | ≥4 | 7 | 13 |
| v4 | 8 | 14 | |
| v5 | ≥9 | 15 | |
| v6 | ≥16 |
Как пользоваться этой таблицей: у нас M = 8, поэтому смотрим только один соответствующий столбец. Считаем vi:
v0 = { кол-во блоков с макс. длиной ≤ 1 } = 4
v1 = { кол-во блоков с макс. длиной = 2 } = 9
v2 = { кол-во блоков с макс. длиной = 3 } = 3
v3 = { кол-во блоков с макс. длиной ≥ 4 } = 0
Вычисляем Хи-квадрат:
Где значения K и R берутся исходя из такой таблицы:
| M | K | R |
|---|---|---|
| 8 | 3 | 16 |
| 128 | 5 | 49 |
| 10000 | 6 | 75 |
Теоретические вероятности πi задаются константами. Например, для K=3 и M=8 рекомендуется взять π0 = 0.2148, π1 = 0.3672, π2 = 0.2305, π3 = 0.1875. (Значения для других K и M приведены в [2]).
Далее вычисляем P-значение:
Если оно > 0.01, как в нашем примере, то последовательность считается достаточно случайной.
Тест рангов бинарных матриц
Тест анализирует матрицы, которые составлены из исходной последовательности, а именно — рассчитывает ранги непересекающихся подматриц, построенных из исходной двоичной последовательности. В основе тест лежат исследования Коваленко [6], где ученый исследовал случайные матрицы, состоящие из 0 и 1. Он показал, что можно спрогнозировать вероятности того, что матрица M x Q будем иметь ранг R, где R = 0,1,2,...min(M,Q). Эти вероятности равны:
NIST рекомендует брать M = Q = 32, а также, чтобы длина последовательности n = M^2 * N. Но мы для примера возьмем M = Q = 3. Далее нужны вероятности PM, PM-1 и PM-2. С небольшой долей погрешности формулу можно упростить, и тогда эти вероятности равны:
Итак, пусть дана последовательность 01011001001010101101. «Раскладываем» ее по матрицам — хватило на 2 матрицы:
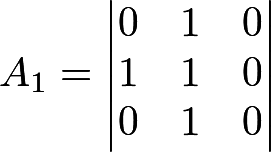
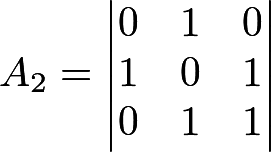
Определяем ранг матриц: получается R1 = 2, R2 = 3. Для теста нужно 3 числа:
- FM = {кол-во матриц с рангом M} = {кол-во матриц с рангом 3} = 1
- FM-1 = 1 (аналогично)
- N — FM — FM-1 = 2 — 1 — 1 = 0
Вычисляем P-значение:
Если результат > 0.01, то последовательность признается случайной. NIST рекомендует, чтобы общая длина последовательности была >= 38MQ.
Спектральный тест
Подопытная последовательность рассматривается как дискретный сигнал, для которого делается спектральное разложение с целью выявить частотные пики. Очевидно, что такие пики будут свидетельствовать о наличии периодических составляющих, что не есть гут. Если вкратце, то тест выявляет пики, превышающие 95%-й барьер, после чего проверяет, не превышает ли доля этих пиков 5%.
Как нетрудно догадаться, для представления последовательности в виде суммы периодических составляющих будем использовать дискретное преобразование Фурье. Оно выглядит так:
Здесь xk — исходная последовательность, в которой единице соответствует +1, а нулю -1, Xj — полученные значения комплексных амплитуд (комплексные означает, что в них содержится как вещественное значение амплитуды, так и фаза).
Вы спросите, а где же здесь периодичности? Ответ — экспоненту можно выразить через тригонометрические функции:
Для нашего теста интересны не фазы, а абсолютные значения амплитуд. И если мы вычислим эти абсолютные значения, то окажется, что они симметричны (это общеизвестный факт при переходе от комплексных значений к вещественным), поэтому для дальнейшего рассмотрения мы возьмём только половину этих значений (от 0 до n/2) — остальные не несут дополнительной информации.
Покажем все это на примере. Пусть задана последовательность 1001010011.
Тогда x = { 1, -1, -1, 1, -1, 1, -1, -1, 1, 1 }.
Вот как разложение Фурье можно сделать, например, в программе GNU Octave:
octave:1> x = [1, -1, -1, 1, -1, 1, -1, -1, 1, 1]
x =
1 -1 -1 1 -1 1 -1 -1 1 1
octave:2> abs(fft(x))
ans =
0.0000 2.0000 4.4721 2.0000 4.4721 2.0000 4.4721 2.0000 4.4721 2.0000 Далее вычисляем граничное значение по формуле
Оно означает, что если последовательность истинно случайная, то 95% пиков не должны превышать эту границу.
Вычислим предельное число пиков, которых должно быть меньше, чем T:
Далее смотрим на результат разложения и видим, что все наши 4 пика меньше граничного значения. Далее оцениваем эту разницу:
Вычисляем P-значение:
Оно получилось >0.01, поэтому гипотеза о случайности принимается. И да, для теста рекомендуется брать не менее 1000 бит.
Тест на встречающиеся непересекающиеся шаблоны
Подопытная последовательность разбивается на блоки одинаковой длины. Например:
1010010010 1110010110В каждом блоке будем искать какой-нибудь шаблон, например «001». Слово непересекающиеся означает, что в случае нахождения шаблона внутри последовательности, следующее сравнение не будет захватывать ни одного бита найденного шаблона. В результате поиска для каждого i-го блока будет найдено число Wi, равное кол-ву найденных случаев.
Итак, для наших блоков W1 = 2 и W2 = 1:
101 001 001 0
111 001 0110
Вычислим математические ожидание и дисперсию, как если бы наша последовательность была подлинно случайна. Ниже приведены формулы. Здесь N = 2 (кол-во блоков), M = 10 (длина блока), m = 3 (длина образца).
Вычислим Хи-квадрат:

Вычислим итоговое P-значение через неполную гамма-функцию:
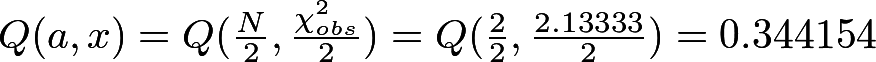
Видим, что P-значение > 0.1, а значит, последовательность достаточно случайна.
Мы оценили только один шаблон. На самом деле нужно проверить все комбинации шаблонов, да и ещё к тому же для разной длины этих шаблонов. Сколько того и другого нужно, определяется исходя из конкретных требований, но обычно m берут 9 или 10. Чтобы получить осмысленные результаты, следует брать N < 100 и M > 0.01 * n.
Тест на встречающиеся пересекающиеся шаблоны
Этот тест отличается от предыдущего тем, что при нахождении шаблона «окно» поиска сдвигается не на длину шаблона, а только на 1 бит. Чтобы не загромождать статью, мы не станем приводить пример расчета по этому методу. Он полностью аналогичен.
Универсальный тест Мауэра
Тест оценивает, насколько «далеко» друг от друга отстоят шаблоны внутри последовательности. Смысл теста в том, чтобы понять, насколько последовательность сжимаема (конечно, имеется в виду сжатие без потерь). Чем более сжимаема последовательность, тем она менее случайна. Алгоритм этого теста весьма громоздкий для Хабра-формата, поэтому опустим его.
Тест на линейную сложность
В основе теста лежит предположение, что подопытная последовательность была получена через регистр сдвига с линейной обратной связью (или LFSR, Linear feedback shift register). Это общеизвестный метод получения бесконечной последовательности: тут каждый следующий бит получается как некая функция бит, «сидящих» в регистре. Минус LFSR в том, что он всегда имеет конечный период, т.е. последовательность обязательно будет рано или поздно повторяться. Чем больше длина LFSR, тем лучше случайная последовательность.
Исходная последовательность разбивается на равные блоки длиной M. Далее для каждого блока с помощью алгоритма Берлекэмпа — Мэсси [10] находится его линейная сложность (Li), т.е. длина LFSR. Затем для всех найденных Li оценивается распределение Хи-квадрат со 6 степенями свободы. Покажем на примере.
Пусть дан блок 1101011110001 (M=13), для которого алгоритм Берлекэмпа — Мэсси выдал L = 4. Убедимся, что это так. Действительно, нетрудно догадаться, что для этого блока каждый следующий бит получается как сумма (по модулю 2) 1-го и 2-го бита (нумерация с 1):
x5 = x1 + x2 = 1 + 1 = 0
x6 = x2 + x3 = 1 + 0 = 1
x7 = x3 + x4 = 1 + 0 = 1
и.т.д.
Вычисляем математическое ожидание по формуле
Для каждого блока вычисляем значение Ti:
Далее на основе множества T вычисляем набор v0,...,v6 таким образом:
- если Ti <= -2.5, то v0++
- если -2.5 < Ti <= -1.5, то v1++
- если -1.5 < Ti <= -0.5, то v2++
- если -0.5 < Ti <= 0.5, то v3++
- если 0.5 < Ti <= 1.5, то v4++
- если 1.5 < Ti <= 2.5, то v5++
- если Ti > 2.5, то v6++
Имеем 7 возможных исходов, а значит вычисляем Хи-квадрат с числом степеней свободы 7 — 1 = 6:
Вероятности πi в тесте жестко заданы и равны соответственно: 0.010417, 0.03125, 0.125, 0.5, 0.25, 0.0625, 0.020833. (πi для большего числа степеней свободы можно вычислить по формулам, данным в [2]).
Вычислить P-значение:
Если результат получился > 0.01, то последовательность признается случайной. Для реальных тестов рекомендуется брать n >= 10^6 и М в пределах от 500 до 5000.
Тест на подпоследовательности
Анализируется частота нахождения всевозможных последовательностей длиной «m» бит внутри исходной последовательности. При этом каждый образец ищется независимо, т.е. возможно как бы «наложение» одного найденного образца на другой. Очевидно, что количество всевозможных образцов будет 2m. Если последовательность достаточно велика и случайна, то вероятности нахождения каждого из этих образцов одинакова. (Кстати, если m = 1, то этот тест «вырождается» в уже описанный ранее тест на соотношение «0» или «1»).
В основе теста лежат работы [8] и [11]. Там описываются 2 показателя (∇ψ2m и ∇2ψ2m), которые характеризуют, насколько частоты появления образцов соответствуют этим же частотам для истинно случайной последовательности. Покажем алгоритм на примере.
Пусть дана последовательность 0011011101 длиной n = 10, а также m = 3.
Сначала формируется 3 новых последовательности, каждая из которых получается добавлением m-1 первых битов последовательности к её концу. Получается:
- Для m = 3: 0011011101 00 (добавили 2 бита к концу)
- Для m-1 = 2: 0011011101 0 (добавили 1 бит к концу)
- Для m-2 = 1: 0011011101 (исходная последовательность)
- v000 = 0, v001 = 1, v010 = 1, v011 = 2, v100 = 1, v101 = 2, v110 = 2, v111 = 0
- v00 = 1, v01 = 3, v10 = 3, v11 = 3
- v0 = 4, v1 = 6
Подставляем:
Тогда:
Итоговые значения:
Итак, оба P-значения > 0.01, а значит последовательность признается случайной.
Приблизительная энтропия
Метод приблизительной энтропии (Approximate Entropy) изначально проявил себя в медицине, особенно в кардиологии. Вообще, согласно классическому определению, энтропия является мерой хаоса: чем она выше, тем более непредсказуемые явления. Хорошо это или плохо, зависит от контекста. Для случайных последовательностей, используемых в криптографии, важно иметь высокую энтропию — это значит, что будет сложно предсказать последующие случайные биты на основе того, что уже имеем. А вот, например, если за случайную величину взять сердечный ритм, измеряемый с заданным периодом, то ситуация иная: есть множество исследований (например, [12]), доказывающих, что чем ниже вариабельность сердечных ритмов, тем реже вероятность инфарктов и прочих неприятных явлений. Очевидно, что сердце человека не может биться с постоянной частотой. Однако одни умирают от инфарктов, а другие нет. Поэтому метод приблизительной энтропии позволяет оценить, насколько с виду случайные явления действительно случайны.
Конкретно, тест вычисляет частоты появления всевозможных образцов заданной длины (m), а затем аналогичные частоты, но уже для образцов длиной m+1. Затем распределение частот сравнивается с эталонным распределением Хи-квадрат. Как и в предыдущем тесте, образцы могут перекрываться.
Покажем на примере. Пусть дана последовательность 0100110101 (длина n = 10), и возьмём m = 3.
Для начала дополним последовательность первыми m-1 битами. Получится 0100110101 01.
Посчитаем встречаемость каждого из 8 всевозможных блоков. Получится:
k000 = 0, k001 = 1, k010 = 3, k011 = 1, k100 = 1, k101 = 3, k110 = 1, k111 = 0.
Посчитаем соответствующие частоты по формуле Cim = ki / n:
C0003 = 0, C0013 = 0.1, C0103 = 0.3, C0113 = 0.1, C1003 = 0.1, C1013 = 0.3, C1103 = 0.1, C1113 = 0.
Аналогичным образом считаем частоты появления подблоков длиной m+1=4. Их уже 24=16:
С00114 = С01004 = С01104 = С10014 = С11014 = 0.1, С01014 = 0.2, С10104 = 0.3. Остальные частоты = 0.
Вычисляем φ3 и φ4 (заметьте, что здесь натуральный логарифм):
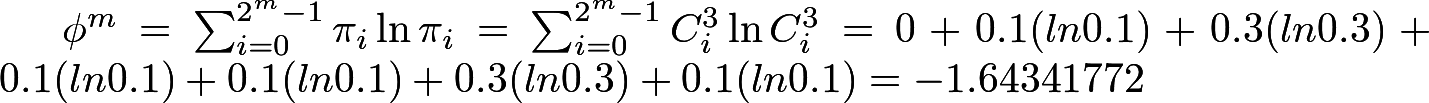

Вычисляем Хи-квадрат:
P-значение:
Получившееся значение > 0.01, а значит последовательность признается случайной.
Тест кумулятивных сумм
Примем каждый нулевой бит исходной последовательности за -1, а каждый единичный — за +1, после чего посчитаем сумму. Интуитивно понятно, что чем более случайна последовательность, тем быстрее эта сумма будет стремиться к нулю. С другой стороны, представим, что дана последовательность, состоящая из 100 нулей и 100 единиц, идущих подряд: 00000...001111...11. Здесь сумма получится равной 0, однако очевидно, что назвать такую последовательность случайной «рука не поднимется». Следовательно, нужен более глубокий критерий. И этим критерием являются частичные суммы. Будем постепенно считать суммы, начиная от первого элемента:
S1 = x1
S2 = x1 + x2 S3 = x1 + x2 + x3…
Sn = x1 + x2 + x3 +… + xn
Далее находится число z = максимум среди этих сумм.
Наконец, считается P-значение по следующей формуле (её вывод см. в [9]):
Где:
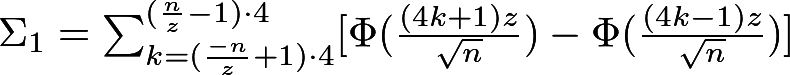

Здесь Φ — функция распределения стандартной нормальной случайной величины. Напоминаем, что стандартное нормальное распределение — это всем известное гауссово распределение (в форме колокола), у которого математическое ожидание 0 и дисперсия 1. Выглядит так:
Если получившееся P-значение > 0.01, то последовательность признается случайной.
Кстати, у этого теста есть 2 режима: первый мы только что рассмотрели, а во втором суммы считаются начиная с последнего элемента.
Тест на произвольные отклонения
Этот тест похож на предыдущий: аналогичным образом считаются частичные суммы нормализованной последовательности (т.е. состоящей из -1 и 1). Пусть дана последовательность 0110110101 и пусть S(i) — это частичная сумма с 1 по i-й элемент. Нанесем эти точки на график, предварительно прибавив «0» к началу и концу последовательности S(i) — это нужно для целостности дальнейших рассчетов:
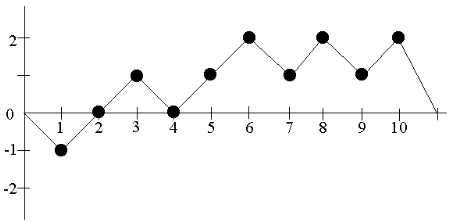
Отметим точки, где график пересекает горизонтальную ось — эти точки будут делить последовательность на т.н. циклы. Здесь мы имеем 3 цикла: {0, -1, 0}, {0, 1, 0} и {0, 1, 2, 1, 2, 1, 2, 0}. Далее, говорят, что каждый из этих циклов последовательно принимает различные состояния. Например, первый цикл 2 раза принимает состояние «0» и 1 раз состояние "-1". Для данного теста интересуют состояния от -4 до 4. Занесем все нахождения в этих состояниях в такую таблицу:
| Состояние (x) | Цикл №1 | Цикл №2 | Цикл №3 |
|---|---|---|---|
| -4 | 0 | 0 | 0 |
| -3 | 0 | 0 | 0 |
| -2 | 0 | 0 | 0 |
| -1 | 1 | 0 | 0 |
| 1 | 0 | 1 | 3 |
| 2 | 0 | 0 | 3 |
| 3 | 0 | 0 | 0 |
| 4 | 0 | 0 | 0 |
На основе этой таблицы формируем другую таблицу: в ней по горизонтали пойдут количества циклов, принимающих заданное состояние:
| Состояние (x) | Ни разу | 1 раз | 2 раза | 3 раза | 4 раза | 5 раз |
|---|---|---|---|---|---|---|
| -4 | 3 | 0 | 0 | 0 | 0 | 0 |
| -3 | 3 | 0 | 0 | 0 | 0 | 0 |
| -2 | 3 | 0 | 0 | 0 | 0 | 0 |
| -1 | 2 | 1 | 0 | 0 | 0 | 0 |
| 1 | 1 | 1 | 0 | 1 | 0 | 0 |
| 2 | 2 | 0 | 0 | 1 | 0 | 0 |
| 3 | 3 | 0 | 0 | 0 | 0 | 0 |
| 4 | 3 | 0 | 0 | 0 | 0 | 0 |
Далее для каждого из восьми состояний вычисляется Хи-квадрат статистики по формуле
Где vk(x) — значения в таблице для данного состояния, J — количество циклов (у нас 3), πk(x) — вероятности того, что состояние «x» возникнет k раз в подлинно случайном распределении (они известны).
Например, для x=1 получается:
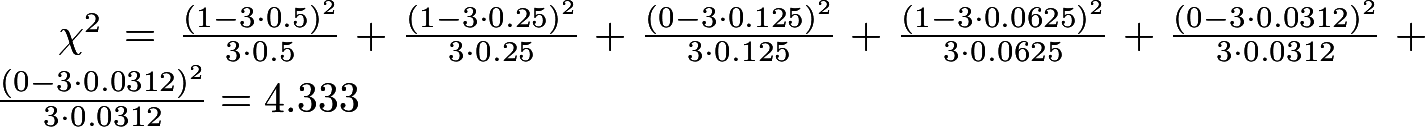
Значения π для остальных x смотрите в [2].
Вычисляем P-значение:
Если оно > 0.01, то делается вывод о случайности. В итоге необходимо вычислить 8 P-значений. Какие-то могут оказаться больше 0.01, какие-то — меньше. В таком случае финальное решение о последовательности делается на основе других тестов.
Разновидность теста на произвольные отклонения
Практически похож на предыдущий тест, но берется более широкий набор состояний: -9, -8, -7, -6, -5, -4, -3, -2, -1, +1, +2, +3, +4, +5, +6, +7, +8, +9. Но главное отличие в том, что здесь Р-значение вычисляется не через гамма-функцию (igamc) и Хи-квадрат, а через функцию ошибок (erfc). За точными формулами читатель может обратиться к исходному документу.
Ниже привожу список источников, которые можно посмотреть, если хочется углубиться в тему:
- csrc.nist.gov/groups/ST/toolkit/rng/stats_tests.html
- csrc.nist.gov/groups/ST/toolkit/rng/documents/SP800-22rev1a.pdf
- Центральная предельная теорема
- Anant P. Godbole and Stavros G. Papastavridis, (ed), Runs and patterns in probability: Selected papers. Dordrecht: Kluwer Academic, 1994
- Pal Revesz, Random Walk in Random and Non-Random Environments. Singapore: World Scientific, 1990
- И. Н. Коваленко, Теория вероятностей и её применения, 1972
- O. Chrysaphinou, S. Papastavridis, “A Limit Theorem on the Number of Overlapping Appearances of a Pattern in a Sequence of Independent Trials.” Probability Theory and Related Fields, Vol. 79, 1988
- I. J. Good, “The serial test for sampling numbers and other tests for randomness,” Cambridge, 1953
- A. Rukhin, “Approximate entropy for testing randomness,” Journal of Applied Probability, 2000
- Алгоритм Берлекэмпа — Мэсси
- D. E. Knuth, The Art of Computer Programming. Vol. 2 & 3, 1998
- www.ncbi.nlm.nih.gov/pubmed/8466069