Я уже частично говорил о работе с FITS-файлами в Octave. Теперь расскажу о применении этого математического пакета для обработки конкретных данных, а именно: для вычисления центра вращения звездного поля по набору снимков, полученных с определенным интервалом.
Для начала коснемся математической части. Геометрические преобразования математически удобно представить в векторно-матричной форме. Так, например, если у нас есть радиус-вектор r, характеризующий данную точку изображения, то чтобы получить радиус-вектор точки — отображения, r' необходимо умножить матрицу геометрического преобразования, A, на r: r' = A·r. В простейшем случае A — двумерная матрица 2х2. Однако, для сложных преобразований ее необходимо расширить до размеров 3х3: например, для описания смещения изображения.
В общем случае векторы r и r' являются векторами-столбцами из трех элементов: собственно координат точки и единицы. Сама матрица преобразования 3х3 имеет лишь шесть значимых элементов (верхние два ряда), а третий ряд ее содержит два нуля и одну единицу.
В этом случае преобразование поворота относительно начала координат на угол θ в матричном виде запишется так:
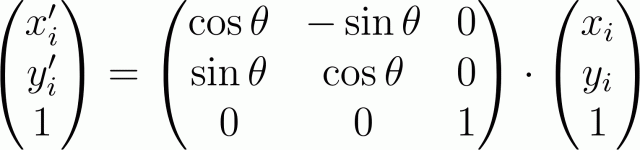
Значимые члены матрицы геометрического преобразования несут следующий смысл: подматрица 2х2 левого верхнего угла отражает преобразования, зависящие от координат точки (например, поворот, масштабирование), а верхние два члена крайнего правого столбца — преобразования, не зависящие от координат (смещение).
Таким образом, например, матрица вращения вокруг начала координат на угол θ с последующим за этим сдвигом на вектор t будет иметь вот такой вид:
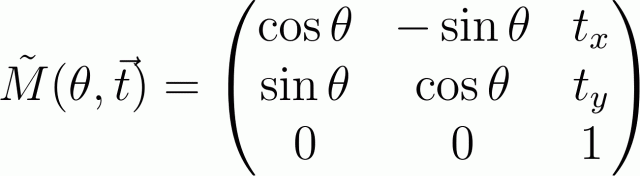
Для получения матрицы, описывающей более сложное преобразование, нам необходимо будет разложить это движение на элементарные (вращение, смещение, масштабирование) и перемножить соответствующие матрицы. Тем, кто работал с openGL не составит труда выполнить подобное. Надо лишь помнить, что если преобразования выполняются в порядке A, B, C, то перемножать их нужно будет «задом наперед»: результирующая матрица M = C·B·A (так как сначала производится преобразование A путем умножения A·r, результирующий вектор испытывает преобразование B и так далее.
Вращение вокруг произвольной точки раскладывается на три элементарных преобразования: сдвиг изображения так, чтобы начало координат находилось в точке вращения (т.е. если центр вращения находится в точке (x, y), сдвинуть нужно на вектор (-x,-y)); вращение его на угол θ и обратный сдвиг на вектор (x,y). В результате этого перемножения матрица преобразования будет иметь вид
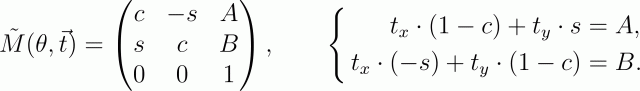
(для упрощения записи я заменил sin θ на s, а cos θ на c).
Если обозначить значимые члены матрицы вращения как матрицу R, то последнюю систему уравнений можно представить в матричном виде (I-R)·t = AB, где AB — вектор-столбец из членов A и B итоговой матрицы преобразования.
Отсюда можно найти вектор t, характеризующий центр изображения: t = (I-R) \ AB, где обратной косой чертой обозначена операция «левого» деления (запись, принятая в Matlab и Octave): в алгебре это аналогично записи t = (I-R)-1AB (I — единичная матрица).
Если вращение сопровождается еще небольшими смещениями, вектор AB будет содержать аддитивное слагаемое dr, которое внесет значительную погрешность в вычисления (т.к. при вращении на малые углы длина вектора AB невелика). Математически определить это смещение невозможно, имея на руках лишь пару снимков. Однако, если мы имеем значительное количество изображений, можно вычислить медианное значение центра вращения, а зная его уже легко будет определить малые смещения dr.
Итак, пусть у нас имеется набор изображений звездного поля (это, кстати, может быть и произвольное изображение с надежно выделяемыми опорными участками) и необходимо вычислить центр вращения этого поля.
Для начала нам необходимо выделить звезды (в общем случае — опорные точки). В конкретном случае это решается простой бинаризацией по заданному порогу (порог выбирается как максимум из величины, заданной пользователем, и суммы медианного значения интенсивности по изображению плюс четверть стандартного отклонения). Далее в полученном бинарном изображении обнаруживаются зоны с 8-связанностью и нумеруются в порядке обнаружения. В итоге мы получаем набор масок, при помощи которых можно вычислить центры объектов (в простейшем случае — как элементарный центр тяжести).
Далее нам необходимо выделить объекты, присутствующие на всех изображениях. Я решил эту проблему «в лоб»: для каждого изображения строится набор векторов — координат обнаруженных объектов в полярной системе относительно каждого объекта (т.е. для набора из N точек получаем N·(N-1) векторов). Для отождествления перебираются все наборы векторов для первого и для i-го изображения. Каждому набору дается оценка — количество совпадений радиус-векторов точек с точностью до устанавливаемой пользователем погрешности dr, dφ. Затем выбирается пара наборов с наивысшей оценкой и объекты i-го изображения нумеруются, в соответствии с порядком объектов первого изображения. После каждой процедуры обнаружения объектов первого изображения на i-м увеличивается значение счетчиков, соответствующих обнаруженным объектам первого изображения. Параллельно ведется накопление координат обнаруженных объектов.
Это решение «в лоб» сильно тормозит вычисления и сильно расходует память в случае большого количества обнаруженных объектов и большого количества изображений, поэтому метод можно упростить. Например, можно сначала сравнить первое и последнее изображение, определившись с набором точек (что уменьшит расход памяти и количество итераций); сам поиск можно тоже производить лишь относительно двух-трех объектов первого изображения (использовать сравнение лишь одного набора нельзя, т.к. конкретный объект может быть не обнаружен на i-м изображении).
После окончания обнаружения объектов мы получаем массив счетчиков. Если объект присутствует на всех изображениях, значение соответствующего счетчика должно быть равно M-1 (M — количество изображений). Все данные, для которых счетчик не равен M-1, удаляются. Далее необходимо лишь попарно сравнить координаты объектов для всех изображений, вычисляя для каждой пары центр вращения по приведенной выше формуле (матрица преобразования вычисляется методом наименьших квадратов). Накопив массив координат центра, найдем реальный центр вращения как медиану от всех координат.
Помимо моего способа я нашел еще один способ в этой статье (McKein et al.). Способ удобен тем, что не требует нахождения матрицы преобразования методом наименьших квадратов. Основан он на том, что вращение около произвольной точки можно представить проще: как вращение сразу относительно начала координат и последующее смещение. Авторы предложили вместо вычисления матрицы преобразования определять угол поворота всей системы (что несложно сделать, воспользовавшись представлением координат объектов в полярной системе координат относительно центра тяжести объектов). По углу поворота вычисляется матрица поворота R. Умножая эту матрицу на радиус-векторы объектов первого изображения, найдем вектор смещения, v (как медиану разности радиус-векторов объектов i-го изображения и полученных радиус-векторов). Центр вращения вычисляется все по той же формуле t = (I-R)-1v.
На большом количестве статистического материала оба способа дали одинаковые результаты. Выбор того или иного способа определяется реализацией: в Octave, например, мой способ вычисляется быстрее, а реализация обоих способов проста; при реализации алгоритма на С проще будет способ McKein сотоварищи.
Вот так выглядит разброс найденных координат центров:
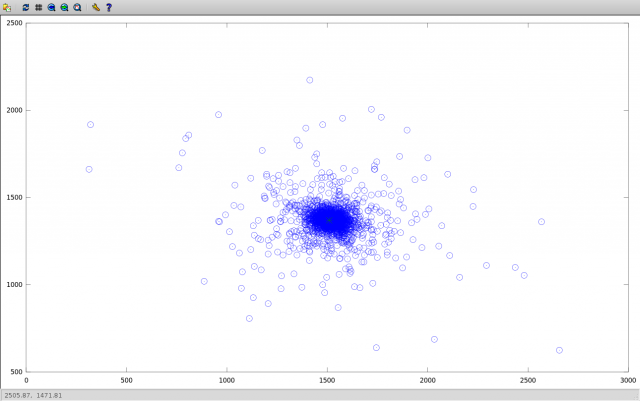
Объясняются выбросы тем, что при сравнении соседних изображений (для которых угол поворота невелик) мы получаем очень высокую погрешность вычисления смещений, сравнимую с погрешностью вычисления координат объектов. Абсолютное отклонение найденных координат относительно медианы иллюстрирует сказанное:
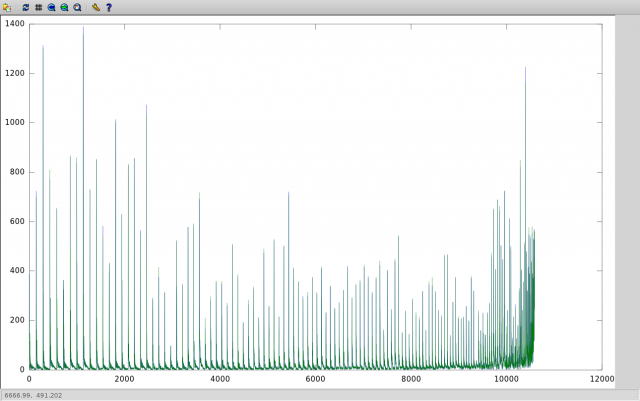
(характерные для близких изображений выбросы затем резко снижаются при увеличении угла поворота). Медианное усреднение позволяет отбросить эти выбросы.
Да, чуть не забыл привести пример изображения звездного поля. Вот оно:

Считывание FITS-файлов:
Вычисление центров объектов:
Вычисление координат объектов относительно объекта с номером N:
Построение набора всех относительных координат объектов для данного изображения:
Получение соответствия номеров объектов на двух изображениях:
Получение массивов координат объектов на всех изображениях в соответствии с их нумерацией на первом изображении:
Получение центра вращения:
То же самое, но методом McKein сотоварищи:
Геометрические преобразования
Для начала коснемся математической части. Геометрические преобразования математически удобно представить в векторно-матричной форме. Так, например, если у нас есть радиус-вектор r, характеризующий данную точку изображения, то чтобы получить радиус-вектор точки — отображения, r' необходимо умножить матрицу геометрического преобразования, A, на r: r' = A·r. В простейшем случае A — двумерная матрица 2х2. Однако, для сложных преобразований ее необходимо расширить до размеров 3х3: например, для описания смещения изображения.
В общем случае векторы r и r' являются векторами-столбцами из трех элементов: собственно координат точки и единицы. Сама матрица преобразования 3х3 имеет лишь шесть значимых элементов (верхние два ряда), а третий ряд ее содержит два нуля и одну единицу.
В этом случае преобразование поворота относительно начала координат на угол θ в матричном виде запишется так:
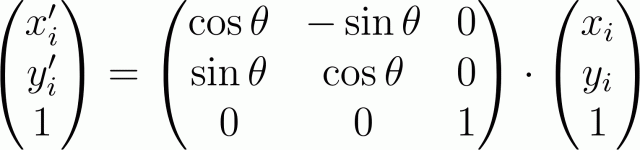
Значимые члены матрицы геометрического преобразования несут следующий смысл: подматрица 2х2 левого верхнего угла отражает преобразования, зависящие от координат точки (например, поворот, масштабирование), а верхние два члена крайнего правого столбца — преобразования, не зависящие от координат (смещение).
Таким образом, например, матрица вращения вокруг начала координат на угол θ с последующим за этим сдвигом на вектор t будет иметь вот такой вид:
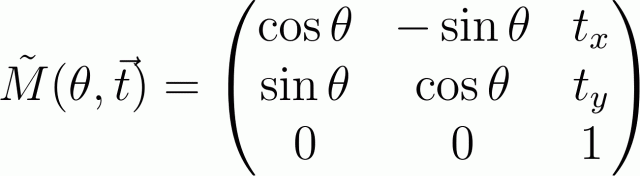
Для получения матрицы, описывающей более сложное преобразование, нам необходимо будет разложить это движение на элементарные (вращение, смещение, масштабирование) и перемножить соответствующие матрицы. Тем, кто работал с openGL не составит труда выполнить подобное. Надо лишь помнить, что если преобразования выполняются в порядке A, B, C, то перемножать их нужно будет «задом наперед»: результирующая матрица M = C·B·A (так как сначала производится преобразование A путем умножения A·r, результирующий вектор испытывает преобразование B и так далее.
Вращение вокруг произвольной точки раскладывается на три элементарных преобразования: сдвиг изображения так, чтобы начало координат находилось в точке вращения (т.е. если центр вращения находится в точке (x, y), сдвинуть нужно на вектор (-x,-y)); вращение его на угол θ и обратный сдвиг на вектор (x,y). В результате этого перемножения матрица преобразования будет иметь вид
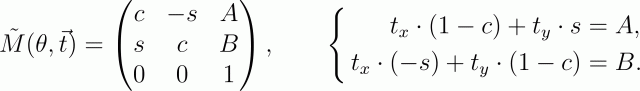
(для упрощения записи я заменил sin θ на s, а cos θ на c).
Если обозначить значимые члены матрицы вращения как матрицу R, то последнюю систему уравнений можно представить в матричном виде (I-R)·t = AB, где AB — вектор-столбец из членов A и B итоговой матрицы преобразования.
Отсюда можно найти вектор t, характеризующий центр изображения: t = (I-R) \ AB, где обратной косой чертой обозначена операция «левого» деления (запись, принятая в Matlab и Octave): в алгебре это аналогично записи t = (I-R)-1AB (I — единичная матрица).
Если вращение сопровождается еще небольшими смещениями, вектор AB будет содержать аддитивное слагаемое dr, которое внесет значительную погрешность в вычисления (т.к. при вращении на малые углы длина вектора AB невелика). Математически определить это смещение невозможно, имея на руках лишь пару снимков. Однако, если мы имеем значительное количество изображений, можно вычислить медианное значение центра вращения, а зная его уже легко будет определить малые смещения dr.
Реализация в Octave
Итак, пусть у нас имеется набор изображений звездного поля (это, кстати, может быть и произвольное изображение с надежно выделяемыми опорными участками) и необходимо вычислить центр вращения этого поля.
Для начала нам необходимо выделить звезды (в общем случае — опорные точки). В конкретном случае это решается простой бинаризацией по заданному порогу (порог выбирается как максимум из величины, заданной пользователем, и суммы медианного значения интенсивности по изображению плюс четверть стандартного отклонения). Далее в полученном бинарном изображении обнаруживаются зоны с 8-связанностью и нумеруются в порядке обнаружения. В итоге мы получаем набор масок, при помощи которых можно вычислить центры объектов (в простейшем случае — как элементарный центр тяжести).
Далее нам необходимо выделить объекты, присутствующие на всех изображениях. Я решил эту проблему «в лоб»: для каждого изображения строится набор векторов — координат обнаруженных объектов в полярной системе относительно каждого объекта (т.е. для набора из N точек получаем N·(N-1) векторов). Для отождествления перебираются все наборы векторов для первого и для i-го изображения. Каждому набору дается оценка — количество совпадений радиус-векторов точек с точностью до устанавливаемой пользователем погрешности dr, dφ. Затем выбирается пара наборов с наивысшей оценкой и объекты i-го изображения нумеруются, в соответствии с порядком объектов первого изображения. После каждой процедуры обнаружения объектов первого изображения на i-м увеличивается значение счетчиков, соответствующих обнаруженным объектам первого изображения. Параллельно ведется накопление координат обнаруженных объектов.
Это решение «в лоб» сильно тормозит вычисления и сильно расходует память в случае большого количества обнаруженных объектов и большого количества изображений, поэтому метод можно упростить. Например, можно сначала сравнить первое и последнее изображение, определившись с набором точек (что уменьшит расход памяти и количество итераций); сам поиск можно тоже производить лишь относительно двух-трех объектов первого изображения (использовать сравнение лишь одного набора нельзя, т.к. конкретный объект может быть не обнаружен на i-м изображении).
После окончания обнаружения объектов мы получаем массив счетчиков. Если объект присутствует на всех изображениях, значение соответствующего счетчика должно быть равно M-1 (M — количество изображений). Все данные, для которых счетчик не равен M-1, удаляются. Далее необходимо лишь попарно сравнить координаты объектов для всех изображений, вычисляя для каждой пары центр вращения по приведенной выше формуле (матрица преобразования вычисляется методом наименьших квадратов). Накопив массив координат центра, найдем реальный центр вращения как медиану от всех координат.
Помимо моего способа я нашел еще один способ в этой статье (McKein et al.). Способ удобен тем, что не требует нахождения матрицы преобразования методом наименьших квадратов. Основан он на том, что вращение около произвольной точки можно представить проще: как вращение сразу относительно начала координат и последующее смещение. Авторы предложили вместо вычисления матрицы преобразования определять угол поворота всей системы (что несложно сделать, воспользовавшись представлением координат объектов в полярной системе координат относительно центра тяжести объектов). По углу поворота вычисляется матрица поворота R. Умножая эту матрицу на радиус-векторы объектов первого изображения, найдем вектор смещения, v (как медиану разности радиус-векторов объектов i-го изображения и полученных радиус-векторов). Центр вращения вычисляется все по той же формуле t = (I-R)-1v.
На большом количестве статистического материала оба способа дали одинаковые результаты. Выбор того или иного способа определяется реализацией: в Octave, например, мой способ вычисляется быстрее, а реализация обоих способов проста; при реализации алгоритма на С проще будет способ McKein сотоварищи.
Вот так выглядит разброс найденных координат центров:

Объясняются выбросы тем, что при сравнении соседних изображений (для которых угол поворота невелик) мы получаем очень высокую погрешность вычисления смещений, сравнимую с погрешностью вычисления координат объектов. Абсолютное отклонение найденных координат относительно медианы иллюстрирует сказанное:

(характерные для близких изображений выбросы затем резко снижаются при увеличении угла поворота). Медианное усреднение позволяет отбросить эти выбросы.
Да, чуть не забыл привести пример изображения звездного поля. Вот оно:

Исходники
Считывание FITS-файлов:
function [image header] = fits_read(filename)
%
% считываем FITS-файл и переворачиваем для правильного отображения
% Координата y отсчитывается в результате сверху!
% (если не делать flipdim, отображаться будет зеркально)
%
% ЗАВИСИМОСТИ:
% read_fits_image (из пакета fits)
%
image = [];
printf("Read file %s ... ", filename); fflush(1);
% проверяем, есть ли такой файл и является ли он файлом:
[ s e m ] = stat(filename);
if(e != 0 || !S_ISREG(s.mode))
printf("No such file!\n"); fflush(1);
return;
endif
[ image header ] = read_fits_image(filename);
if(!isempty(image))
image = flipdim(image',1); % переворачиваем, чтобы отображалось верно
printf("OK!\n");
else
printf("Bad image!\n");
endif
fflush(1);
endfunction
Вычисление центров объектов:
function [ xc, yc ] = find_centers(Img, treshold)
% [ xc, yc ] = find_centers(Img, treshold)
% Нахождение центров пятен изображения Img с интенсивностью выше treshold
% xc, yc - массивы координат
%
tmp = zeros(size(Img));
mm = mean2(Img) + std2(Img)/4; % считаем простенький порог
tres1 = max(mm, treshold);
printf("\nTreshold: %g\n", tres1); fflush(stdout);
tmp(find(Img > tres1)) = 1;
tmp = medfilt2(logical(tmp));
[ Labels, Nlabels ] = bwlabel(tmp);
if(Nlabels < 1)
printf(stderr, "\nError! There's no spots!!!\n\n");
return
endif
[yy, xx] = ndgrid(1:size(Img,1),1:size(Img,2));
xc = []; yc = [];
for i = [1 : Nlabels]
idxs = find(Labels == i);
Is = sum(Img(idxs));
xc = [ xc sum(Img(idxs) .* xx(idxs)) / Is ];
yc = [ yc sum(Img(idxs) .* yy(idxs)) / Is ];
end
endfunction
Вычисление координат объектов относительно объекта с номером N:
function coords = find_tree(xc, yc, N)
%
% coords = find_tree(xc, yc, N)
% для заданных массивов координат пятен, xc и yc, вычисляет вектора от точки
% с номером N до остальных точек в полярной системе координат.
% возвращает матрицу, в которой первая колонка - полярная координата
% вектора, вторая - угловая координата.
%
if(size(xc, 1)) == 1 % проверяем, являются ли массивы координат столбцами
xc = xc';
endif
if(size(yc, 1)) == 1
yc = yc';
endif
if(size(xc) != size(yc) || N > size(xc, 1)) % проверяем размеры
coords = [];
endif
xn = xc(N); yn = yc(N); % координаты N-й точки
Dx = xc - xn; Dy = yc - yn; % смещения остальных точек относительно N-й
R = sqrt(Dx.^2+Dy.^2); % полярная координата
Phi = atan2(Dy,Dx)*180/pi; % угловая координата
coords = [R Phi];
endfunction
Построение набора всех относительных координат объектов для данного изображения:
function [Tree xc yc] = get_tree(treshold, i)
%
% [Tree xc yc] = get_tree(treshold, i)
% Поиск дерева векторов расстояний между точками и координат центров этих точек
% Вход:
% treshold - порог интенсивности для бинаризации изображения
% i - номер кадра в серии
% Выход:
% Tree - трехмерный массив с расстояниями между точками, у которого
% * первая координата - номер второй точки в паре
% * вторая координата - полярные координаты вектора расстояния между точками
% * третья координата - номер первой точки в паре
% xc, yc - координаты центров
%
% ЗАВИСИМОСТИ:
% fits_read
% find_tree
% find_centers
%
Tree = []; xc = []; yc = [];
name = sprintf("object_%04d.fit", i);
II = fits_read(name);
if(isempty(II)) return; endif
printf("Find centers of %s ... ", name); fflush(1);
[xc, yc] = find_centers(II, treshold);
for j = 1:size(xc,2)
Tree(:,:,j) = find_tree(xc, yc, j);
endfor
printf("done (%d vectors)!\n", size(Tree, 1));
endfunction
Получение соответствия номеров объектов на двух изображениях:
function coord_indexes = find_cluster_c(CC, CC1, dR, dPhi)
%
% coord_indexes = find_cluster_c(CC, CC1, dR, dPhi)
% Поиск соответствия индексов объектов из CC объектам из CC1
% Вход:
% CC, CC1 - массивы векторов для двух соседних изображений
% dR - погрешность по R (если |r1-r0| < dR, считается, что r1 == r0)
% dPhi - аналогичная погрешность по угловой координате
% Выход:
% coord_indexes - массив соответствия индексов точек изображений [индекс1 индекс2; ...]
%
Ncc = size(CC, 3); Ncc1 = size(CC1, 3); % кол-во групп точек в каждом кластере
Cluster = []; % массив по строкам: кол-во совпадений, индекс1, индекс2, угол поворота
for jj = 1 : Ncc % цикл по группам первого набора
Nnear = []; % массив, в который будет складываться кол-во близких точек для каждого кластера
PhiMed = []; % медианы углов поворота
r0 = CC(:,1,jj); phi0 = CC(:,2,jj);
for ii = 1 : Ncc1 % цикл по группам второго набора
r1 = CC1(:,1,ii); phi1 = CC1(:,2,ii);
points = {}; % объединение для поиска соответствия точек (номер точки 1; номера близких точек в 2)
dphi_s = []; % массив, в который будут заноситься для анализа найденные углы
for i = 1:size(r0); % цикл по векторам первого набора
d = abs(r1-r0(i)); % разности между векторами
idx = find(d < dR); % ищем наиболее близкие по r
if(isempty(idx)) continue; endif; % близких нет - идем дальше
points = [ points; {i, idx} ]; % добавляем номера похожих точек
endfor
for i = 1:size(points, 1)
dphi = abs(phi1(points{i,2}) - phi0(points{i,1}));
dphi_s = [dphi_s; dphi];
endfor
if(isempty(dphi_s)) continue; endif;
dphi = median(dphi_s); % примерный угол поворота набора 2 относительно 1
n = size(find(abs(dphi_s-dphi)<dPhi), 1);
Nnear = [ Nnear, n ]; % формируем массив
PhiMed = [ PhiMed, dphi ];
endfor
idx = find(Nnear == max(Nnear))(1); % нашли номер набора, наиболее близкого к jj-му
Cluster = [ Cluster; Nnear(idx) jj idx PhiMed(idx) ];
endfor
% теперь ищем соответствие точек в наборе
n = max(Cluster(:,1)); % максимальное соответствие
idx = find(Cluster(:,1) == n)(1); % на всякий случай берем самое первое
first = Cluster(idx, 2); % номер набора на изображении 1
second = Cluster(idx, 3); % -//- 2
Phi = Cluster(idx, 4); % угол поворота 2 относительно 1
r0 = CC(:,1,first); phi0 = CC(:,2,first);
r1 = CC1(:,1,second); phi1 = CC1(:,2,second);
coord_indexes = [];
for i = 1:size(r0); % цикл по векторам первого набора
d = abs(r1-r0(i)); % разности между векторами
idx = find(d < dR); % ищем наиболее близкие по r
if(isempty(idx)) continue; endif; % близких нет - идем дальше
dphi = abs(abs(phi1(idx) - phi0(i)) - Phi);
if(size(idx, 1) != 1) % несколько точек
n = find(dphi == min(dphi))(1); % номер наиболее близкой точки
idx = idx(n);
dphi = dphi(n);
endif
if(dphi > dPhi) continue; endif; % близких нет - идем дальше
coord_indexes = [ coord_indexes; i idx ];
endfor
endfunction
Получение массивов координат объектов на всех изображениях в соответствии с их нумерацией на первом изображении:
function [X Y] = get_centers(i0, i1, treshold, dR, dPhi)
%
% [X Y] = get_centers(i0, i1, treshold, dR, dPhi)
% Помещает в массивы X,Y координаты центров пятен для каждой пары
% изображений
% Вход:
% i1, in - начальный и конечный номера изображений
% treshold - порог для поиска пятен
% dR, dPhi - допуск по полярным координатам (чтобы считать точки близкими)
% Выход:
% X, Y - матрицы набора центров для пятен
% номер строки соответствует номеру объекта для первого изображения
% номер столбца - номер изображения
% координаты в каждой строке - для одного и того же объета
%
% ЗАВИСИМОСТИ:
% get_tree -> fits_read, find_tree, find_centers
% find_cluster_c
%
n = 1; % счетчик изображений + координата текущего столбца в X,Y
i_start = i0; % номер первого изображения для сравнения
CS = [];
printf("\nimage 1\n", i);
do
[CC xc yc] = get_tree(treshold, i_start);
im1 = i_start;
i_start++;
until(!isempty(CC) || i_start > i1)
X = xc'; Y = yc'; % первый столбец - первое изображение
Counters = zeros(size(X)); % и сразу заполняем нулями массив счетчиков
for i = i_start:i1
[CC1 xc1 yc1] = get_tree(treshold, i);
if(isempty(CC1)) continue; endif
printf("\nimage %d, ", ++n);
% все сравнения идут с первым изображением
indexes = find_cluster_c(CC, CC1, dR, dPhi);
printf("%d points\n\n", size(indexes, 1));
% Заполняем координаты:
X(indexes(:,1),n) = xc1(indexes(:,2));
Y(indexes(:,1),n) = yc1(indexes(:,2));
% и увеличиваем счетчик для найденных пятен
Counters(indexes(:,1))++;
endfor
% стираем объекты, не присутствующие на всех изображениях
idx = find(Counters != n-1);
X(idx,:) = []; Y(idx,:) = [];
endfunction
Получение центра вращения:
function [Xc Yc] = matr_center(X, Y)
%
% [Xc Yc] = matr_center(X, Y)
% Вычисляет координаты центра кадра, исходя из матричных операций
% Вход:
% X, Y - массивы с координатами пятен (из функции get_centers)
% Выход:
% Xc, Yc - массив центров кадров
%
Xc = []; Yc = [];
imax = size(X,2);
for i = 1:imax-1
for j = i+1:imax
% выделяем координаты объектов
X0 = X(:,i)';
X1 = X(:,j)';
Y0 = Y(:,i)';
Y1 = Y(:,j)';
% получаем примерный угол поворота изображения (вектора - от центра тяжести)
vec0X = X0 - mean(X0); vec0Y = Y0 - mean(Y0);
vec1X = X1 - mean(X1); vec1Y = Y1 - mean(Y1);
% Следующий код можно раскомментировать, если используется выборка из малого количества изображений
%phi0 = atan2(vec0Y, vec0X); phi1 = atan2(vec1Y, vec1X);
%% прибавляем к отрицательным 2пи, чтобы избежать переходов -pi+a -> pi-b
%phi0(find(phi0<0)) += 2*pi; phi1(find(phi1<0)) += 2*pi;
%dphi = median(phi1 - phi0); % медианный угол поворота изображения
%R = [cos(dphi) -sin(dphi); sin(dphi) cos(dphi)]; % матрица поворота
%RR1 = R * [vec0X;vec0Y]; % вектора, которые получились бы при повороте системы 0
%dR = sqrt((vec1X-RR1(1,:)).^2+(vec1Y-RR1(2,:)).^2); % расхождения между реальными и теоретическими
%idx = find(dR < median(dR)+std(dR)); % отсекаем явные промахи
%if(size(idx,2) < 3) % слишком много промахов
%printf("Image %d: too much bad data\n", i);
%continue;
%endif
%X0 = X0(idx); X1 = X1(idx);Y0 = Y0(idx); Y1 = Y1(idx);
% получаем матрицу геометрического преобразования
A = [X1;Y1;ones(size(X1))]/[X0;Y0;ones(size(X1))];
% вычисляем примерные координаты центра
CRDS = (eye(2)-A(1:2,1:2)) \ A(1:2,3);
Xc = [Xc CRDS(1)]; Yc = [Yc CRDS(2)]; % накапливаем центры
endfor
endfor
Xmed = median(Xc)
Ymed = median(Yc)
endfunction
То же самое, но методом McKein сотоварищи:
function [Xc Yc] = matr_center_notmine(X, Y)
%
% [Xc Yc] = matr_center(X, Y)
% Вычисляет координаты центра кадра, исходя из матричных операций
% Вход:
% X, Y - массивы с координатами пятен (из функции get_centers)
% Выход:
% Xc, Yc - массив центров кадров
%
Xc = []; Yc = [];
imax = size(X,2);
for i = 1:imax-1
for j = i+1:imax
% выделяем координаты объектов
X0 = X(:,i)';
X1 = X(:,j)';
Y0 = Y(:,i)';
Y1 = Y(:,j)';
% получаем примерный угол поворота изображения (вектора - от центра тяжести)
vec0X = X0 - mean(X0); vec0Y = Y0 - mean(Y0);
vec1X = X1 - mean(X1); vec1Y = Y1 - mean(Y1);
phi0 = atan2(vec0Y, vec0X); phi1 = atan2(vec1Y, vec1X);
% прибавляем к отрицательным 2пи, чтобы избежать переходов -pi+a -> pi-b
phi0(find(phi0<0)) += 2*pi; phi1(find(phi1<0)) += 2*pi;
dphi = median(phi1 - phi0); % медианный угол поворота изображения
R = [cos(dphi) -sin(dphi); sin(dphi) cos(dphi)]; % матрица поворота
% Получаем вектор v
v = median(R * [X0; Y0] - [X1; Y1], 2);
% вычисляем примерные координаты центра
CRDS = (eye(2)-R) \ v;
%printf("Center: (%g, %g)\n", CRDS(1), CRDS(2));
Xc = [Xc -CRDS(1)]; Yc = [Yc -CRDS(2)]; % накапливаем центры
endfor
endfor
Xmed = median(Xc)
Ymed = median(Yc)
endfunction