 Один мой друг, историк по профессии, подкинул мне замечательную идею об использовании древней мнемонической и счетной систем в современной криптографии. В процессе его рассказов об узелковой письменности Инков, я начал соображать, что все новое — хорошо забытое старое и было бы не плохо как-то применить древний опыт в современном мире. Первое, что пришло в голову — криптография. Это самое очевидное — просто сконвертировать узлы с ниток в байты и шифр готов. С одной стороны все казалось понятным, но потом я вспомнил про криптостойкость и другие параметры шифров и понял, что не обладаю достаточным опытом и знаниями в области криптографии, чтобы в одиночку разработать новый шифр.
Один мой друг, историк по профессии, подкинул мне замечательную идею об использовании древней мнемонической и счетной систем в современной криптографии. В процессе его рассказов об узелковой письменности Инков, я начал соображать, что все новое — хорошо забытое старое и было бы не плохо как-то применить древний опыт в современном мире. Первое, что пришло в голову — криптография. Это самое очевидное — просто сконвертировать узлы с ниток в байты и шифр готов. С одной стороны все казалось понятным, но потом я вспомнил про криптостойкость и другие параметры шифров и понял, что не обладаю достаточным опытом и знаниями в области криптографии, чтобы в одиночку разработать новый шифр. Дальше я решил попытаться представить некий эзотерический язык программирования, конструкции которого могут быть записаны с помощью узелковой письменности Кипу. Поначалу казалось, что это невозможно: я придумывал язык и пытался написать на нем программу вычисления факториала. Первые три черновика спецификаций ушли в урну: языки никуда не годились. Они выглядели как полагалось для эзотерических языков, но не помогали мне решать поставленную задачу, т.к. не были полными по Тьюрингу. Энтузиазм потихоньку угасал и эта задача казалась мне не по-плечу. Собравшись с силами, я решил, что если смогу написать программу вычисления факториала — то язык работает.
Четвертая версия языка оказалось удачной: я написал факториал, затем генерацию последовательности Фибоначи и дюжину простых примерчиков аля “сумма чисел от 0 до 99”. Язык получился что надо: необычный и в тоже время с простой понятной идеей. Главное — язык может решить любую (ну или почти любую) задачу которую можно выразить в виде вычислимой функции.
Инки и Кипу
(Абзац из Википедии)
Ки́пу — древняя мнемоническая и счётная система Инков, своеобразная письменность: представляет собой сложные верёвочные сплетения и узелки, изготовленные из шерсти южноамериканских верблюдовых (альпаки и ламы) либо из хлопка. В кипу может быть от нескольких свисающих нитей до 2000. Она использовалась для передачи сообщений посыльными часки по специально проложенным имперским дорогам, а также в самых разных аспектах общественной жизни (в качестве календаря, топографической системы, для фиксации налогов и законов, и др.).
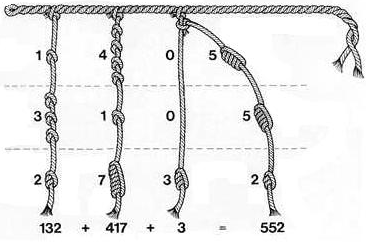
В кипу использовалась десятичная система счисления и преимущественно на них записывались числа с помощью трех видов узлов. Первые изображали десятки, вторые — группу единиц (2-9) и третий узел обозначал единицу. Таким образом, группа узлов интерпретировалась как число, в котором на месте тысяч, сотен, десяток и единиц были навязаны соответствующие узлы.
Положим что запись “7d” — обозначает последовательность из 7 узлов обозначающих десятки. “5i” — группу единичных узлов из 5 штук и “I” — единицу, а “x” — как пропуск. Тогда число 703 можно представить следующей последовательностью узлов: “7dx3i”, число 2013 — 2dx1d3i и и т.д.
Эти идеи и легли в основу языка Quipu за некоторыми изменениями.
Спецификации языка
Программа на Quipu представляет собой матрицу узелков (knots), каждый столбец которой образует нить (thread). Количество нитей ограничено числом 26, по количеству символов в латинском алфавите (на самом деле их 52, но об этом позже). Количество узелков на нити не ограничено. Каждая нить должна быть отделена от соседних как минимум одним пробелом и быть выравненной на фиксированное количество отступов от начала файла на всем ее протяжении. Иными словами нить в виде “лесенки”, а не столбца сложно назвать валидной.
Quipu может оперировать двумя типами данных — целыми числами и строками.
Программа исполняется по нитям (сначала первая нить, потом вторая и т.д) сверху в низ. На каждом шаге исполнения вычисляется значение текущего узелка. Исполнение продолжается до тех пор, пока не будет вычислено значение последнего узелка последней нити или не встретится узелок останов. “::”.
Узелки можно разделить на два типа — простые и составные. Простые состоят из одной ячейки матрицы (пара символов в строке, например “$a”). Составные узелки представляют собой последовательность простых узелков в нити. Составные узелки используются для представления чисел и строк. Например строку “Habr” на языке Quipu можно записать так:
‘H
‘a
‘b
‘r
А число 2013 так:
2#
1@
3&
Каждая нить может быть обозначена символьной меткой. Если меток нет — все нити нумеруются по-порядку метками “a” — “z”. Кроме того, каждая нить имеет свое значение, которое равно значению последнего в ней узелка. Обращаться к значению нити можно с помощью специального узелка — “$a” (значение нити “a”). Значение каждой нити записывается в ее нулевой узелок, что позволяет использовать его как неявный аргумент в выражениях.
Нить имеет две составляющие — основную и инициализирующую. Например “a:” — инициализирующая составляющая нити “а”, “а.” — основная. Нить может представляться как двумя составляющими, так и каждой в отдельности. В последовательном исполнении программы используются только основные нити. Инициализирующие нити исполняются единожды при первом явном или неявном обращении к значению нити. Под явным подразумевается исполнение узелка “$a”, под неявным — использование верхнего нулевого узелка нити в выражениях. Если у нити нет инициализирующей составляющей, то ее начальное значение равно нулю. Существует ограничение на виды узелков, используемые в инициализирующих нитях: запрещается использовать узелки меняющие поток выполнения программы, т.е. переходы и узелок «останов.».
Некоторые узлы не имею своего собственного значения, поэтому их значение вычисляется как значение ближайшего значащего узелка перед ними (если таких нет — то значению нити, которое является нулевым узелком). Примерами таких узелков служат узелки вывода и условных переходов.
Таблица узелков (n — текущий узел нити)
| Узелок | Значение |
|---|---|
| $a | Значение нити «а». |
| >> | Ввод значения с терминала. |
| << | Вывод значения (n-1) узла в терминал. |
| 1#4%5@1& | Число 1451: "#" — тысячи, "%" — сотни, "@" — десятки, "&" — единицы. |
| -- | Разница между (n — 2) и (n — 1) узелками. |
| ++ | Сумма (n — 2) и (n — 1) узелков. |
| ** | Произведение узелка (n — 2) и узелка (n — 1). |
| // | Целочисленное деление узелка (n — 2) на узелок (n — 1). |
| %% | Остаток от деления нацело узелка (n — 2) на узелок (n — 1). |
| <c | Условный переход на нить «с», если значение предыдущего узла меньше нуля. |
| >c | Условный переход на нить «c», если значение предыдущего узла больше нуля. |
| =с | Условный переход на нить «с», если значение предыдущего узла равно нулю. |
| ? с | Безусловный переход на нить «с». |
| :: | Останов. |
| ' | Символ. |
| \n | Спец символ. |
Примеры программ
Hello World!
a: a.
'H <<
'e
'l
'l
'o
'
'W
'o
'r
'l
'd
'!
\n
Сумма чисел от 0 до 99
s. i. c. e.
$i 1& $i $s
++ ++ 1% <<
--
=e
?s
Факториал
a: a. b: b. e.
>> $a 1& $a $b
=e 1& <<
1& ++
-- $b
=e **
?a
Фибоначчи
s. f. d. a: b: a. b. x: i. t. o. e.
$x $x ', 1& 1& $b $f >> 1& 1& 1& '.
=e 2& ' ?i ++ << << <<
1& -- << ?f ', ?e
-- $i $f '
=o -- << ?o
1& =e
-- $a
=t $b
1& ++
<<
',
'
<<
1&
<<
Реализация
Довольно давно меня преследует мысль о том, что пора бы изучить новый язык, для расширения кругозора так-сказать. Выбор пал на Scala. Меня всегда привлекала ее так называемая “чрезмерная сложность” о которой все говорят. Написав пару простых примеров аля “Hello World”, я возомнив себя прожженным скалистом, взялся за реализацию интерпретатора Quipu. Задача оказалась сложнее, чем я думал, не смотря на то, что в самом начале дал себе установку — сделать, что бы просто работало, не зацикливаясь на красоте дизайна и реализации.
В итоге, рабочий прототип я получил за полтора дня. Получил, действительно то, что хотел. Этакий proof-of-concept идеи. Кода написал довольно немного и выглядит он слегка пугающим особенно для людей имеющих опыт разработки на Scala. Однако, я считаю, что начало положено. Путь “идея -> реализация” пройден минимальными усилиями и следующие шаги могут быть направлены на улучшение текущей реализации. Я даже не исключаю возможности, что придется все переписывать с нуля, но все-же надеюсь, что разумное зерно в первоначальном коде есть и его может спасти масштабный рефакторинг.
В текущей реализации также есть пара незначительных проблем, которые я решил пока не фиксить, в свете перспективы “все переписывания с нуля”. Тем не менее проблемы эти больших неудобств не доставляют а даже наоборот приучают Quipu программистов правильно оформлять свои программы. Ниже приведен список текущих недочетов:
1) Каждая нить должна иметь метку. Нити без меток не поддерживаются.
2) Программа должна заканчиваться пустой строкой, иначе — узлы, находящиеся на последней строке не будут синтерпретированы.
Итак. Исходные коды интерпретатора доступны на GitHub: github.com/vkostyukov/quipu. Я буду очень рад pull-request’ам с исправлениями моего кодобреда. Кроме того, буду признателен за новые примеры использования языка, которые я обязательно размещу на странице проекта. Еще обещаю стилизованную футболку с надписью “%username%, the first Quipu hacker.” тому, кто напишет программу 99-bottles-of-beer на Quipu. Шутка :)
Зачем?
Есть убеждение, что придумывая новый язык программирования, автор практически обрекает себя на неудачу. С этим я полностью согласен и считаю, что на ближайшие 3-5 лет ресурс по языкам программирования у человечества есть. Сейчас уже сложно придумать, что-то новое, полезное и отличное от известных всем кофейных гигантов. Но это пожалуй справедливо для языков “больших” и “серьезных”, которые пытаются решить все мыслимые и немыслимые проблемы с которыми якобы сталкивается разработчик.
Эзотерические же языки решают другие проблемы — проблемы разминки мозгов, нездорового любопытства и